双曲线典型例题
- 格式:doc
- 大小:1.02 MB
- 文档页数:7



班级姓名座号2.2.1 双曲线及其标准方程(二)※典型例题A,两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,例2已知B求炮弹爆炸点的轨迹方程。
例3 如图,点B A ,的坐标分别为()0,5-,()0,5,直线BM AM ,相交于点M ,且它们的斜率之积是94,使求点M 的轨迹方程,并由点M 的轨迹方程判断轨迹的形状。
与2.1例3比较,你有什么发现?例4 已知定点()0,3A 和定圆()163:22=++y x C ,定圆与圆C 相外切,并过点A ,求动圆圆心P 的轨迹方程。
※ 课堂练习1. 如图,圆O 的半径为定长r ,A 是圆O 外一个定点,P 是圆上任意一点。
线段AP 的垂直平分线l 和直线OP 相交于点Q ,当点P 在圆上运动时,点Q2.相距1400m 的B A ,两个哨所,听到炮弹爆炸声的时间相差3s ,已知声速是340m/s ,问炮弹爆炸点在怎样的曲线上,为什么?三、小结反思1.双曲线8822=-ky kx 的一个焦点为()3,0,那么k 等于 ( )A .1 B.-1 C.97 D. 97- 2.已知两圆()24:221=++y x C ,()24:222=+-y x C ,动圆M 与两圆21,C C 都相切,则动圆圆心M 的轨迹方程是 ( )A .0=x B.)2(114222≥=-x y x C. 114222=-y x D. 114222=-y x 或0=x 3.已知()0,51-F ,()0,51F ,动圆P 满足a PF PF 221=-,当a 为3和5时,点P 的轨迹分别是( )A .双曲线和一条直线B .双曲线和一条射线C .双曲线的一支和一条直线D .双曲线的一支和一条射线4.求到定点()0,c F 与到定直线c a x l 2:=距离之比是⎪⎭⎫ ⎝⎛>1a c a c 的点M 的轨迹.。
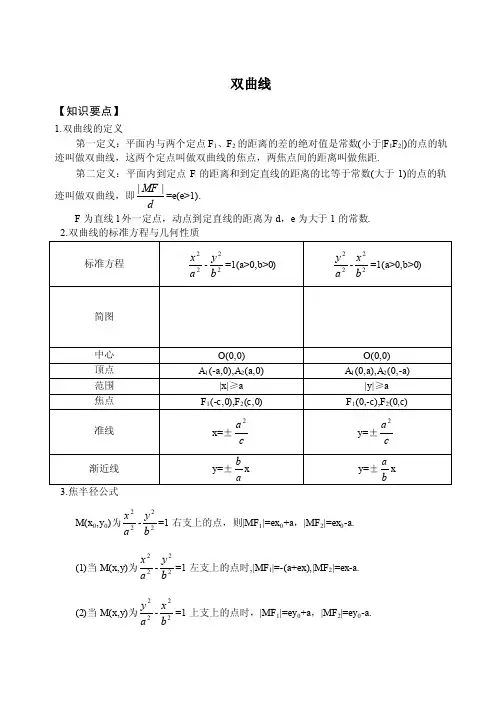
双曲线【知识要点】1.双曲线的定义第一定义:平面内与两个定点F 1、F 2的距离的差的绝对值是常数(小于|F 1F 2|)的点的轨迹叫做双曲线,这两个定点叫做双曲线的焦点,两焦点间的距离叫做焦距.第二定义:平面内到定点F 的距离和到定直线的距离的比等于常数(大于1)的点的轨迹叫做双曲线,即dMF ||=e(e>1). F 为直线l 外一定点,动点到定直线的距离为d ,e 为大于1的常数. 2.双曲线的标准方程与几何性质M(x 0,y 0)为22a x -22b y =1右支上的点,则|MF 1|=ex 0+a ,|MF 2|=ex 0-a.(1)当M(x,y)为22a x -22b y =1左支上的点时,|MF 1|=-(a+ex),|MF 2|=ex-a.(2)当M(x,y)为22a y -22bx =1上支上的点时,|MF 1|=ey 0+a ,|MF 2|=ey 0-a.【基础训练】1.(2004年春季北京)双曲线42x -92y =1的渐近线方程是 ( )A.y =±23xB.y =±32xC.y =±49xD.y =±94x2.过点(2,-2)且与双曲线22x -y 2=1有公共渐近线的双曲线方程是( )A.22y -42x =1B.42x -22y =1C.42y -22x =1D.22x -42y =13.如果双曲线642x -362y =1上一点P 到它的右焦点的距离是8,那么P 到它的右准线距离是( )A.10B.7732 C.27 D.5324.已知圆C 过双曲线92x -162y =1的一个顶点和一个焦点,且圆心在此双曲线上,则圆心到双曲线中心的距离是____________. 5.求与圆A :(x +5)2+y 2=49和圆B :(x -5)2+y 2=1都外切的圆的圆心P 的轨迹方程为________________.【典型例题】题型一:求双曲线的标准方程例1、 根据下列条件,求双曲线的标准方程:(1)与双曲线92x -162y =1有共同的渐近线,且过点(-3,23);(2)与双曲线162x -42y =1有公共焦点,且过点(32,2).(3)实轴长为16,离心率为45e(4)经过两点P )7,26()72,3(---Q题型二:双曲线的定义及应用例2、(2002年全国,19)设点P 到点M (-1,0)、N (1,0)距离之差为2m ,到x 轴、y 轴距离之比为2,求m 的取值范围.例3、如下图,在双曲线122y -132x =1的上支上有三点A (x 1,y 1),B (x 2,6),C (x 3,y 3),它们与点F (0,5)的距离成等差数列. (1)求y 1+y 3的值;(2)证明:线段AC 的垂直平分线经过某一定点,并求此点坐标.变式:、已知(2,1),A F ,P 是曲线221(0)x y x -=>上一点,当||||2PA PF +取最小值时,P 的坐标是,|||PA PF 最小值是 .题型三:双曲线的性质及应用例4、 已知双曲线22a x -22by =1的离心率e >1+2,左、右焦点分别为F 1、F 2,左准线为l ,能否在双曲线的左支上找一点P ,使得|PF 1|是P 到l 的距离d 与|PF 2|的等比中项?变式:过双曲线22a x -22by =1.的右焦点F 作渐近线的垂线,垂足为M ,交双曲线的左右两支于A 、B 两点,求双曲线离心率的取值范围。

第9节 双曲线渐近线的几个常用结论知识与方法设双曲线2222:1x y C a b-=()0,0a b >>的焦点分别为1F 、2F ,则有以下结论:1.双曲线的焦点到渐近线的距离等于虚半轴长b .2.如图1所示,以12F F 为直径的圆与双曲线C 的渐近线在第一象限的交点为(),a b . 3.如图2所示,过双曲线C 上任意一点P 作C 的两条渐近线的平行线,则它们与两条渐近线所围成的平行四边形PIOJ 的面积是定值2ab.4.如图3所示,双曲线C 上任意一点P 处的切线与C 的两条渐近线分别交于A 和B 两点,则P 为AB 的中点,且AOB 的面积为定值ab .5.如图4所示,A 、B 分别在双曲线C 的两条渐近线上,D 为AB 的中点,若直线OD 、AB的斜率都存在,则它们的斜率之积为22b a.典型例题【例1】已知双曲线()222:10x C y a a-=>的右焦点为F ,则F 到双曲线C 的渐近线的距离为_______.变式 已知双曲线()22:10C x y a -=>的右焦点为F ,过F 且与x 轴垂直的直线与双曲线C 交于A 、B 两点,则A 、B 两点到双曲线的一条渐近线的距离之和为_______.【例2】如下图所示,双曲线22:13y C x -=的左、右焦点分别为1F 、2F ,以12F F 为直径的圆与双曲线C 的渐近线交于A 、B 、D 、E 四点,则四边形ABDE 的面积为_______.变式 (2019·新课标Ⅰ卷)已知双曲线2222:1x yC a b -=()0,0a b >>的左、右焦点分别为1F 、2F ,过1F 的直线与C 的两条渐近线分别交于A 、B 两点,若1F A AB =,120F B F B ⋅=,则C 的离心率为_______.【例3】已知双曲线22:126x y C -=的右焦点为F ,点A 为双曲线C 在第一象限上的一点,且AF x ⊥轴,过A 作C 的两条渐近线的平行线与双曲线的渐近线交于M 、N 两点,则四边形OMAN 的面积为_______.变式 已知A 为双曲线222:16x y C a -=()0a >的右顶点,过A 作C 的两条渐近线的平行线,分别与双曲线的渐近线交于M 、N 两点,若四边形OMAN 3则双曲线C 的离心率为_______.【例4】已知双曲线22:155x y C -=,过点()2,0P 的直线l 与双曲线C 有且仅有1个公共点,且直线l 与双曲线的两条渐近线分别交于点A 和B ,则AOB 的面积为_______.【例5】已知直线320x y -+=与双曲线2222:1x y C a b-=()0,0a b >>的渐近线交于A 、B 两点,若AB 的中点为()1,1M ,则双曲线C 的渐近线方程为_______.变式 (2014·浙江)设直线30x y m -+=()0m ≠与双曲线22221x y a b-=()0,0a b >>的两条渐近线分别交于点A 、B ,若点(),0P m 满足PA PB =,则该双曲线的离心率是_______.强化训练1.(★)已知双曲线22:124x y C -=的一个焦点为F ,则F 到双曲线C 的渐近线的距离为_______.2.(2018·天津·★★★)已知双曲线22221x y a b-=()0,0a b >>的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A 、B 两点.设A 、B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126d d +=,则双曲线的方程为( )A.221412x y -= B.221124x y -= C.22139x y -= D.22193x y -= 3.(★★★)己知双曲线2222:1x y C a b-=()0,0a b >>的左、右焦点分别为1F 、2F ,过1F 的直线与双曲线C 的一条渐近线交于点P ,且12PF PF ⊥,直线1PF 与双曲线的另一渐近线交于点Q ,若12FQ QP =,则双曲线C 的离心率为_______. 4.(★★★)已知双曲线2222:1x y C a b-=()0,0a b >>的左、右焦点分别为1F 、2F ,过1F 且斜率为12的直线与双曲线C 的渐近线在第一象限交于点P ,若12PF PF ⊥,则双曲线C 的离心率为_______.5.(★★★)己知P 为双曲线2222:1x y C a b-=上一点,过P 作C 的两条渐近线的平行线,与两条渐近线分别交于M 、N 两点,则平行四边形OMPN 的面积为_______.6.(★★★)已知直线20x y -+=与双曲线()22:10y C x b b-=>的两条渐近线分别交于A 、B 两点,若AB 的中点为28,33M ⎛⎫⎪⎝⎭,则b =_______.7.(★★★★)已知双曲线2222:1x y C a b-=()0,0a b >>的右焦点为()2,0F ,左、右顶点分别为A 和B ,且P 为C 上不与A 、B 重合的一点,直线PA 、PB 的斜率之积为3. (1)求双曲线C 的方程;(2)过点P 的直线l 与双曲线C 有且仅有1个交点,与C 的渐近线交于M 、N 两点,求MON 的面积.。

双曲线和抛物线复习【典型例题】【双曲线A】例1. 已知圆C方程为,定点A(-3,0),求过定点A且和圆C外切的动圆圆心P的轨迹方程。
解析:∵圆P与圆C外切,∴|PC|=|PA|+2,即|PC|-|PA|=2,∴由双曲线定义,点P的轨迹是以A,C为焦点,2为实轴长的双曲线的左支,其中,故所求轨迹方程为点评:在利用双曲线第一定义解题时,要特别注意对定义中“绝对值”的理解,以避免解题时出现片面性。
当P满足时,点P的轨迹是双曲线的一支;当时,点P的轨迹是双曲线的另一支,当时,点P的轨迹是两条射线。
不可能大于。
例 2. 如图,以和为焦点的椭圆的离心率,它与抛物线交于两点,以为两渐近线的双曲线上的动点P(x,y)到一定点Q(2,0)的距离的最小值为1,求此双曲线方程。
解析:由条件知,椭圆中则∴椭圆方程为。
解方程组得两点的坐标分别为(3,2),(3,-2)。
∴所求双曲线的渐近线方程为又Q(2,0)到的距离为所以双曲线的实轴只能在x轴上。
设所求双曲线方程为,则,方程化为,得∵P(x,y)在双曲线上,∴①当,即时,当时,解得∴所求双曲线方程为②当,即时,当时,解得或(舍去),∴所求双曲线方程为综上,所求双曲线方程为或点评:待定系数法是求曲线方程最常用的方法之一。
(1)与双曲线有共同渐近线的双曲线方程可表示为;(2)若双曲线的渐近线方程是,则双曲线的方程可表示为;(3)与双曲线共焦点的双曲线方程可表示为;(4)过两个已知点的双曲线的标准方程表示为;(5)与椭圆有共同焦点的双曲线方程表示为=1利用上述结论求关于曲线的标准方程,可简化解题过程,提高解题速度。
例3. 已知双曲线的中心在原点,焦点在坐标轴上,离心率为,且过点。
(1)求双曲线方程;(2)若点M(3,m)在双曲线上,求证:;(3)求的面积。
解析:(1),∴可设双曲线方程为∵过点,∴,即,∴双曲线方程为(2)由(1)可知,双曲线中,∵点(3,m)在双曲线上,∴故(3)的底,的高点评:双曲线的标准方程和几何性质中涉及到很多基本量,如“a,b,c,e”等,树立基本量思想对于确定曲线方程和认识其几何性质有很大帮助.另外,渐近线是双曲线特有的,双曲线的渐近线方程可记为.同时以为渐近线的双曲线方程可设为()。

双曲线及其方程 (第一课时)一、 教学目标:掌握双曲线的定义、标准方程及其推导。
二、 重点:双曲线的定义和标准方程。
难点:标准方程的推导。
三、 基本概念:1、双曲线的定义: 叫做双曲线的焦点。
叫做双曲线的焦距。
2、注意:0〈2a<21F F =2c3、思考:当2a=2c 时轨迹如何? ,当2a>2c 时又如何?四、 双曲线的标准方程及其推导。
(一) 双曲线的标准方程的推导: 1.建立直角坐标系:2.写出适合条件的动点M 的集合:3.列方程:4.化简方程:(二) 双曲线的标准方程:1、焦点在X 轴上时: 2、焦点在Y 轴上时: 3、a 、 b 、 c 的关系 五、典型例题:例1、根据下列条件,求双曲线的标准方程:(1) 两个焦点的坐标分别是(-5,0),(5,0), 双曲线上的点与两个焦点的距离的差的绝对值等于8; (2) 两个焦点的坐标分别是(0,-6),(0,6),且双曲线经过点A (-5,6).思考:如果已知点M (x,y )与点F 1(-5,0)的距离比它与点F 2(5,0)的距离大8,求M 点的轨迹方程。
并与例1(1)比较有什么联系和区别?例2、已知双曲线1453622=-y x (1)求此双曲线的左、右焦点F 1,F 2的坐标;(2) 如果此双曲线上一点P 与焦点F 1的距离等于16,求点P 与焦点F 2的距离六、基本练习:1、根据下列条件,求双曲线的标准方程: (1)a=3,b=4, 焦点在X 轴上;(2)两个焦点的坐标分别是F 1(0,-6), F 2 (0,6), 经过点A (2,-5).(3) 焦点在X 轴上,经过点P (4,-2)和点Q (2,622);(4) a=5,c=8;2、已知双曲线方程1201622=-x y (1)求双曲线的焦点F 1,F 2的坐标。
(2)如果此双曲线上一点P 与焦点F 1的距离等于8,求点P 与焦点F 2的距离。
七、巩固提高:1、若11222=+++λλy x 表示双曲线,则λ的取值范围2、求中心在原点,两对称轴都在坐标轴上,并且经过P (3,415)和Q (,3165)两点的双曲线方程。

双曲线基本知识点及例题优选版1. 过双曲线的一个焦点作x轴的垂线,求垂线与双曲线的交点到两焦点的距离。
2. 已知双曲线的离心率为2,求它的两条渐近线的夹角。
3. 在面积为1的△PMN中,,建立适当坐标系,求以M、N为焦点且过点P的双曲线方程。
4. 已知椭圆和双曲线有相同的焦点,P是两条曲线的一个交点,求的值。
5. 已知椭圆及点B(0,-2),过左焦点F1与点B的直线交椭圆于C、D两点,椭圆的右焦点为F2,求△CDF2的面积。
6. P为椭圆上任意一点,F1为它的一个焦点,求证以焦半径F1P为直径的圆与以长轴为直径的圆相切。
7. 已知两定点A(-1,0),B(1,0)及两动点M(0,y1),N(0,y2),其中,设直线AM与BN的交点为P。
(1)求动点P的轨迹C的方程;(2)若直线与曲线C位于y轴左边的部分交于相异两点E、F,求k 的取值范围。
8. 直线只有一个公共点,求直线l的方程。
1. 解:∵双曲线方程为,∴=13,于是焦点坐标为设过点F1垂直于x轴的直线l交双曲线于,∴故垂线与双曲线的交点到两焦点的距离为。
2. 解:设实轴与渐近线的夹角为,则∴∴两条渐近线的夹角为[点评](1)离心率e与。
(2)要注意两直线夹角的范围,否则将有可能误答为。
3. 解:以MN所在直线为x轴,MN的中垂线为y轴建立直角坐标系,设,(如图所示)则解得设双曲线方程为,将点∴所求双曲线方程为点评:选择坐标系应使双曲线方程为标准形式,然后采用待定系数法求出方程。
4. 解:∵P在椭圆上,,又∵点P在双曲线上,,①、②两式分别平方得两式相减得,∴5. 解:∵,由∵与椭圆有两个公共点,设为:∴又点F2到直线BF1的距离说明:本题也可用来解。
6. 略解1设为椭圆上任意一点,则又两圆半径分别为,,故此两圆内切。
略解2如图,∴此两圆内切7. 解:(1)由题意得AM的方程为,BN的方程为:。
两式相乘,得(2)由8. 解:由(1)∴此时直线l:x=3与双曲线只有一个公共点(3,0);(2)当b≠0时,直线l方程为。
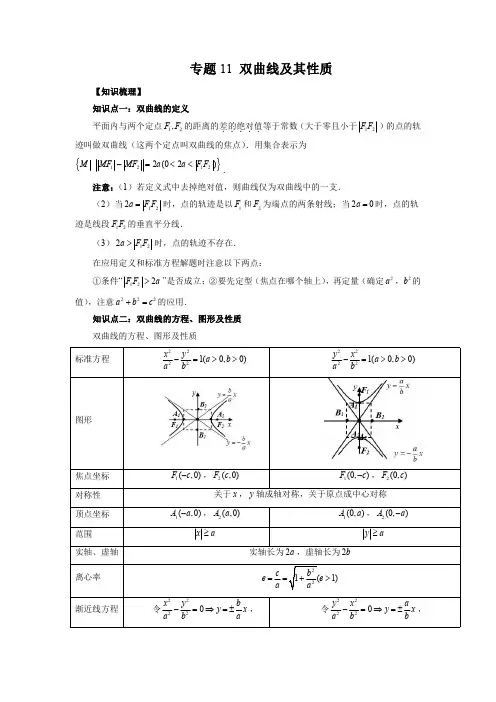
专题11双曲线及其性质【知识梳理】知识点一:双曲线的定义平面内与两个定点12,F F 的距离的差的绝对值.....等于常数(大于零且小于12F F )的点的轨迹叫做双曲线(这两个定点叫双曲线的焦点).用集合表示为{}12122(02)MMF MF a a F F -=<<.注意:(1)若定义式中去掉绝对值,则曲线仅为双曲线中的一支.(2)当122a F F =时,点的轨迹是以1F 和2F 为端点的两条射线;当20a =时,点的轨迹是线段12F F 的垂直平分线.(3)122a F F >时,点的轨迹不存在.在应用定义和标准方程解题时注意以下两点:①条件“122F F a >”是否成立;②要先定型(焦点在哪个轴上),再定量(确定2a ,2b 的值),注意222a b c +=的应用.知识点二:双曲线的方程、图形及性质双曲线的方程、图形及性质A 222121sinsin21cos tanFr r bθθθ==⋅=-考点2:双曲线方程的充要条件考点3:双曲线中焦点三角形的周长与面积及其他问题考点4:双曲线上两点距离的最值问题考点5:双曲线上两线段的和差最值问题考点6:离心率的值及取值范围考点7:双曲线的简单几何性质问题考点8:利用第一定义求解轨迹考点9:双曲线的渐近线考点10:共焦点的椭圆与双曲线【典型例题】考点1:双曲线的定义与标准方程1.(2022·江西科技学院附属中学高二期中(理))已知O为坐标原点,设F1,F2分别是双曲线x2-y2=1的左、右焦点,P为双曲线左支上任意一点,过点F1作∠F1PF2的平分线的垂线,垂足为H,则|OH|=()A.1B.2C .4D .12【答案】A【解析】如图所示,延长F 1H 交PF 2于点Q ,由PH 为∠F 1PF 2的平分线及PH ⊥F 1Q ,易知1PHF PHQ ∽,所以|PF 1|=|PQ |.根据双曲线的定义,得|PF 2|-|PF 1|=2,即|PF 2|-|PQ |=2,从而|QF 2|=2.在△F 1QF 2中,易知OH 为中位线,则|OH |=1.故选:A.2.(2022·黑龙江·铁人中学高二期中)双曲线222112x y a -=(0a >)的左、右两个焦点分别是1F 与2F ,焦距为8;M 是双曲线左支上的一点,且15MF =,则2MF 的值为()A .1B .9C .1或9D .9或13【答案】B【解析】依题意4c =,所以21216a +=,即2a =,因为15MF =,且2124MF MF a -==,所以29MF =.故选:B3.(2022·天津·耀华中学高二期中)与椭圆22:11612y x C +=共焦点且过点(的双曲线的标准方程为()A .2213y x -=B .2221yx -=C .22122y x -=D .2213y x -=【答案】C【解析】椭圆C 的焦点坐标为()0,2±,设双曲线的标准方程为()222210,0y xa b a b -=>>,由双曲线的定义可得2a ==-=a ∴,2c =,b ∴==,因此,双曲线的方程为22122y x -=.故选:C.4.(2022·河北·高二期中)已知双曲线22221x y a b-=的左、右焦点分别为1F ,2F ,O 为坐标原点,1210F F =,点M 是双曲线左支上的一点,若OM =1243MF MF =,则双曲线的标准方程是()A .224121x y -=B .221214x y -=C .22124y x -=D .22124x y -=【答案】C【解析】由题意知:双曲线22221x y a b -=的焦距为210c =,22225a b c ∴+==,125OM OF OF ===,12MF MF ∴⊥.1243MF MF =,不妨设13MF k =,24MF k =,由双曲线的定义可得:212MF MF k a -==,16MF a ∴=,28MF a =,由勾股定理可得:()()222222121268100100MF MF a a a F F +=+===,解得:21a =,224b ∴=,∴双曲线方程为22124y x -=.故选:C.5.(2022·北京工业大学附属中学高二期中)已知双曲线的上、下焦点分别为()10,3F ,()20,3F -,P 是双曲线上一点且124PF PF -=,则双曲线的标准方程为()A .22145x y -=B .22154x y -=C .22145y x -=D .22154y x -=【答案】C【解析】设双曲线的标准方程为()222210,0y x a b a b-=>>,半焦距为c ,则由题意可知3c =,24a =,即2a =,故222945b c a =-=-=,所以双曲线的标准方程为22145y x -=.故选:C .6.(2022·广西·钦州一中高二期中(文))已知平面内两定点()13,0F -,()23,0F ,下列条件中满足动点P 的轨迹为双曲线的是()A .127PF PF -=±B .126PF PF -=±C .124PF PF -=±D .22126PF PF -=±【答案】C【解析】由题意,因为126F F =,所以由双曲线的定义知,当1206PF PF <-<时,动点P 的轨迹为双曲线,故选:C.7.(2022·福建·南靖县第一中学高二期中)(1)求以(-4,0),(4,0)为焦点,且过点的椭圆的标准方程.(2)已知双曲线焦点在y 轴上,焦距为10,双曲线的渐近线方程为20x y ±=,求双曲线的方程.【解析】(1)由题意可设所求椭圆的标准方程为221259x y λλ+=++.又椭圆过点,将x =3,y9151259λλ+=++,解得λ=11或=21λ-(舍去).故所求椭圆的标准方程为2213620x y +=.(2)由题意,设双曲线的标准方程为22221(0,0)y x a b a b -=>>,设焦距为2c ,∴22212210a b c a b c ⎧+=⎪⎪=⎨⎪=⎪⎩,解得5a b c ⎧=⎪⎪=⎨⎪=⎪⎩,∴该双曲线的方程为221520y x -=.8.(2022·黑龙江·大兴安岭实验中学高二期中)求满足下列条件的双曲线的标准方程:(1)焦点分别为(0,6)-,(0,6),且经过点(5,6)A -;(2)经过点,(4,--;【解析】(1)由题易知焦点在y 轴上,设双曲线的方程22221y x a b -=则222223636251c a b a b ⎧=+=⎪⎨-=⎪⎩解得:221620a b ⎧=⎨=⎩所以所求双曲线的标准方程为2211620y x -=(2)设双曲线的方程为:221(0)Ax By AB +=<代入点坐标得到:9+10=11624=1A B A B ⎧⎨+⎩解得:1418A B ⎧=⎪⎪⎨⎪=-⎪⎩故双曲线的标准方程为:22148x y -=考点2:双曲线方程的充要条件9.(多选题)(2022·全国·高二期中)已知曲线22:1C mx ny +=.则()A .若m >n >0,则C 是椭圆B .若m =n >0,则C 是圆C .若mn <0,则C 是双曲线D .若m =0,n >0,则C 是两条直线【答案】ABCD【解析】A 选项,当0m n >>时,22221111x y mx ny m n+=⇒+=,110m n<<,方程表示焦点在y 轴上的椭圆,A 选项正确.B 选项,当0m n =>时,222211mx ny x y n+=⇒+=,表示圆,B 选项正确.C 选项,当0mn <时,22221111x y mx ny m n+=⇒+=,表示双曲线,C 选项正确.D 选项,当0,0m n =>时,22211mx ny y y n +=⇒=⇒=±±D 选项正确.故选:ABCD10.(2022·河南·高二期中(文))已知k ∈R ,则“23k <<”是“方程22162x y k k -=--表示双曲线”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】A【解析】由方程22162x y k k -=--表示双曲线可得()()620k k -->,解得26k <<,显然23k <<能推出26k <<,反之26k <<不能推出23k <<,故“23k <<”是“方程22162x y k k -=--表示双曲线”的充分不必要条件.故选:A.11.(2022·吉林·辽源市田家炳高级中学校高二期中(理))“0mn <”是“方程221x y m n+=表示的曲线为双曲线”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】C【解析】当0mn <,则0m >且0n <或0m <且0n >,此时方程221x y m n+=表示的曲线一定为双曲线;则充分性成立;若方程221x y m n+=表示的曲线为双曲线,则0mn <,则必要性成立,故选:C .考点3:双曲线中焦点三角形的周长与面积及其他问题12.(2022·安徽·淮北师范大学附属实验中学高二期中)已知1F 、2F 是等轴双曲线22:1C x y -=的左、右焦点,点P 在C 上,1260F PF ∠=,则12PF PF ⋅等于___________.【答案】4【解析】∵双曲线C 的方程为:221x y -=,∴221a b ==,得c =由此可得()1F 、)2F ,焦距12=F F ∵1260F PF ∠=,∴2221212122cos 60F F PF PF PF PF =+-,即2212128PF PF PF PF -⋅=+,①又∵点P 在双曲线22:1C x y -=上,∴1222PF PF a -==,平方得22112224PF PF PF PF -⋅+=,②①-②,得124PF PF ⋅=,故答案为:4.13.(2022·上海金山·高二期中)已知1F 、2F 分别为双曲线22221(0,0)x y a b a b-=>>的左、右焦点,若点2F 到该双曲线的渐近线的距离为2,点P 在双曲线上,且1260F PF ∠=︒,则三角形12F PF 的面积为___________.【答案】【解析】双曲线22221(0,0)x y a b a b -=>>的渐近线的方程为b y x a=±,右焦点2(,0)F c 由点2F 到该双曲线的渐近线的距离为22bca =,则2b =由()12222121222||2cos 60PF PF a c PF PF PF PF ⎧-=⎪⎨=+-⋅⎪⎩,可得212416PF PF b ⋅==则三角形12F PF的面积为1211sin 601622PF PF ⋅⋅=⨯=故答案为:14.(多选题)(2022·湖南省汨罗市第二中学高二期中)已知点P 是双曲线E :221169x y -=的右支上一点,1F ,2F 为双曲线E 的左、右焦点,12PF F △的面积为20,则下列说法正确的是()A .点P 的横坐标为203B .12PF F △的周长为803C .12F PF ∠小于3πD .12PF F △的内切圆半径为34【答案】ABC【解析】因为双曲线22:1169x y E -=,所以5c =,又因为12112102022PF F P P Sc y y =⋅=⋅⋅=,所以4P y =,将其代入22:1169x yE -=得2241169x -=,即203x =,所以选项A 正确;所以P 的坐标为20,43⎛⎫± ⎪⎝⎭,由对称性可知2133PF ==,由双曲线定义可知1213372833PF PF a =+=+=所以12PF F △的周长为:12133780210333PF PF c ++=++=,所以选项B 正确;可得11235PF k =,2125PF k =,则(121212360535tan 12123191535F PF -==∈⨯+⨯,则123F PF π<∠,,所以选项C 正确;因为12PF F △的周长为803,所以121202803PF F S r =⋅⋅=,所以32r =,所以选项D 不正确.故选:ABC.15.(2022·四川·阆中中学高二期中(文))已知12F F ,为双曲线C :221164x y-=的两个焦点,P ,Q 为C 上关于坐标原点对称的两点,且12PQ F F =,则四边形12PFQF 的面积为________.【答案】8【解析】由题意得,4,2,a b c ===,由双曲线的对称性以及12PQ F F =可知,四边形12PFQF 为矩形,所以122221228480PF PF a PF PF c ⎧-==⎪⎨+==⎪⎩,解得128PF PF =,所以四边形12PFQF 的面积为128PF PF =.故答案为:8.16.(2022·广东·江门市第二中学高二期中)双曲线2216416y x -=上一点P 与它的一个焦点的距离等于1,那么点P 与另一个焦点的距离等于___________.【答案】17【解析】由双曲线的方程可得实半轴长为8a =,虚半轴长为4b =,故8045c =因为点P 与一个焦点的距离等于1,而8451a c +=+>,故点P 与该焦点同在x 轴的上方或下方,故点P 与另一个焦点的距离为1217a +=,故答案为:17.17.(2022·新疆维吾尔自治区喀什第二中学高二期中(理))已知双曲线22145x y -=的左、右焦点分别为1F ,2F ,点P 是双曲线左支上一点且128PF PF +=,则1221sin sin PF F PF F ∠=∠______.【答案】3【解析】因为双曲线为22145x y -=,所以2a =、3c =,因为点P 是双曲线左支上一点且128PF PF +=,所以214PF PF -=,所以12=PF ,26PF =,在12PF F △中,由正弦定理可得122112sin sin PF PF PF F PF F =∠∠,所以212211sin 3sin PF PF F PF F PF ∠==∠;故答案为:318.(2022·天津市咸水沽第二中学高二期中)已知1F ,2F 分别是双曲线221916x y -=的左、右焦点,AB 是过点1F 的一条弦(A ,B 均在双曲线的左支上),若2ABF 的周长为30,则||AB =___________.【答案】9【解析】双曲线221916x y -=,得a =3,因为A ,B 均在双曲线的左支上,所以21212,2AF AF a BF BF a -=-=,则△ABF 2的周长为()()22112224AF BF AB AF a BF a AB AB a ++=++++=+,所以2|AB |+4×3=30,所以9AB =.故答案为:9.19.(2022·吉林·白城一中高二期中)双曲线221916x y -=的两个焦点为12,F F ,点P 在双曲线上,若1PF ·2PF =0,则点P 到x 轴的距离为________.【答案】165【解析】设()12,,PF m PF n m n ==>,由题意可知3,4,5a b c ==∴=,=6m n -1PF ·2PF =0,2221212PF PF F F ∴+=2224m n c ∴+=,22100m n ∴+=,22=6100m n m n -⎧⎨+=⎩,32m n ∴=1211=222F PF Smn c y =,=c y mn ∴,=mn y c ∴,16=5y ∴,∴点P 到x 轴的距离为165.故答案为:16520.(2022·上海市崇明中学高二期中)已知双曲线221169x y -=的两个焦点分别为1F 、2F ,P 为双曲线上一点,且122F PF π∠=,则12F PF △的面积为_________.【答案】9【解析】依题意,双曲线221169x y -=的焦点1(5,0)F -、2(5,0)F ,12||||||8PF PF -=,因122F PF π∠=,则有222212121212||||||(||||)2||||F F PF PF PF PF PF PF =+=-+,即有22122||||10836PF PF =-=,解得12||||18PF PF =,所以12F PF △的面积121||||92S PF PF ==.故答案为:921.(2022·江苏·高二专题练习)双曲线()222210,0x y a b a b-=>>过焦点1F 的弦AB ,A 、B 两点在同一支上且长为m ,另一焦点为2F ,则2ABF 的周长为().A .4aB .4a -mC .4a +2mD .4a -2m【答案】C【解析】由双曲线的定义得:212BF BF a -=①,212AF AF a -=②,两式相加得:21214BF BF AF AF a -+-=,即22224BF AF AB BF AF m a +-=+-=,所以224BF AF a m +=+,故2ABF 的周长为2242BF AF AB a m ++=+.故选:C22.(2022·新疆·乌鲁木齐101中学高二期中(文))设1F ,2F 是双曲线22146x y -=的左、右焦点,P 为双曲线上一点,且213PF PF =,则12PF F △的面积等于()A .6B .12C.D.【答案】A【解析】双曲线22146x y -=的实半轴长2a =,半焦距c =12||F F =,因213PF PF =,由双曲线定义得22124PF PF PF -==,解得22PF =,16PF =,显然有22122124||0PF PF F F +==,即12PF F △是直角三角形,所以12PF F △的面积12121||||62PF F S PF PF ==.故选:A23.(2022·辽宁大连·高二期中)已知1F ,2F 分别是双曲线221916x y -=的左、右焦点,若P 是双曲线左支上的点,且1232PF PF ⋅=.则12F PF △的面积为()A .8B.C .16D.【答案】C【解析】因为P 是双曲线左支上的点,所以216PF PF -=,两边平方得221212236PF PF PF PF +-⋅=,所以22121236236232100PF PF PF PF +=+⋅=+⨯=.在12F PF △中,由余弦定理得2221212121212100100cos 022PF PF F F F PF PF PF PF PF +--∠==⋅⋅,所以1290F PF ∠=︒,所以121211321622F PF S PF PF =⋅=⨯=△.故选:C考点4:双曲线上两点距离的最值问题24.(2022·上海中学东校高二期末)过椭圆221(9)9x y m m m +=>-右焦点F 的圆与圆22:4O x y +=外切,该圆直径FQ 的端点Q 的轨迹记为曲线C ,若P 为曲线C 上的一动点,则FP 长度最小值为()A .0B .12C .1D .2【答案】C【解析】椭圆221(9)9x y m m m +=>-,3c ==,所以()3,0F .设以FQ 为直径的圆圆心为C ,如图所示:因为圆O 与圆C 外切,所以2OC CF -=,因为12QF OC =,2QF CF =,所以()1124QF QF OC CF F F -=-=<,所以Q 的轨迹为:以1,F F 为焦点,24a =的双曲线的右支.即2,3,a c b ====:C ()221245x y x -=≥.所以P 为曲线C 上的一动点,则FP 长度最小值为1c a -=.故选:C25.(2022·安徽省宣城市第二中学高二阶段练习(理))已知12,F F 分别是双曲线2214xy -=的左、右焦点,P 为双曲线右支上异于顶点的任意一点,若12PF F △内切圆圆心为I ,则圆心I 到圆22(1)1y x +-=上任意一点的距离最小值为()A .2B1C .1D 2【答案】C【解析】设12PF F △的内切圆分别与12,PF PF 切于点,A B ,与12F F 切于点M ,则11||||,||||PA PB F A F M ==,22||||F B F M =.又点P 在双曲线右支上,12||||2PF PF a ∴-=,即12(||||)(||||)2PA F A PB F B a +-+=,12||||2F M F M a ∴-=①,又12||||2F M F M c +=②,由①+②,解得1||F M a c =+,又1||OF c =,则(,0)M a ,因为双曲线2214x y -=的2a =,所以内切圆圆心I 与在直线2x =上,设0(2,)I y ,设圆22(1)1y x +-=的圆心为C ,则(0,1)C ,所以||CI =,当01y =时,min ||2CI =,此时圆22(1)1y x +-=上任意一点的距离最小值为min ||1211CI -=-=.故选:C .26.(2022·101中学高二期末)双曲线22142x y C -=:的右焦点为F ,点P 在椭圆C 的一条渐近线上.O 为坐标原点,则下列说法错误的是()A B .双曲线22142-=y x 与双曲线C 的渐近线相同C .若PO PF ⊥,则PFO △D .PF【答案】B【解析】A.因为双曲线方程为22142x y C -=:,所以2,a b c ===,则c e a ==故正确;B.双曲线22142x y C -=:的渐近线为y =,双曲线22142-=y x 的渐近线方程为y =,故错误;C.设(),P x y ,因为点P在渐近线上,不妨设渐近线方程为y =,即为直线PO 的方程,又因为PO PF ⊥,所以直线PF的方程为y x =,由22y x y x ⎧=⎪⎨⎪=⎩,解得3x y ⎧=⎪⎪⎨⎪=⎪⎩,即P ⎝⎭,所以12S =,故正确;D.)F,其中一条渐近线为y =,则PF 的最小值为点F到渐近线的距离,即d ==.故选:B27.(2022·北京八中高二期中)已知定点A 、B ,且|AB |=4,动点P 满足||PA |﹣|PB ||=3,则|PA |的最小值是()A .12B .32C .72D .5【答案】A【解析】由动点P 满足||PA |﹣|PB ||=3,且3AB <故可得点P 的轨迹为以,A B 为左右焦点的双曲线,故可得23,24a c ==,解得3,22a c ==,由双曲线的几何性质可得PA 的最小值为12c a -=.故选:A.考点5:双曲线上两线段的和差最值问题28.(2022·湖南·长沙市南雅中学高二期中)设双曲线C :22124y x -=的左焦点和右焦点分别是1F ,2F ,点A 是C 右支上的一点,则128AF AF +的最小值为___________.【答案】8【解析】由双曲线C :22124y x -=,可得21a =,224b =,所以22225c a b =+=,所以1a =,5c =,由双曲线的定义可得1222AF AF a -==,所以122AF AF =+,所以1222882AF AF AF AF +=++,由双曲线的性质可知:24AF c a ≥-=,令2AF t =,则4t ≥,所以122288822AF AF t AF AF t +=++=++,记82y t t=++,设124t t ≤<,则121212882(2)y y t t t t -=++-++121212()(8)t t t t t t --=0<,所以12y y <,即82y t t=++在[)4,+∞上单调递增,所以当4t =时,取得最小值84284++=,此时点A 为双曲线的右顶点(1,0).故答案为:8.29.(2022·黑龙江·鸡西市第一中学校高二期中)P 是双曲线22145x y -=的右支上一点,M 、N 分别是圆()2232x y ++=和()2231x y -+=上的点,则|PM |-|PN |的最大值为_________.【答案】5【解析】设双曲线的左右焦点为12,F F ,则1224PF PF a -==,圆()2232x y ++=的圆心为1(3,0)F -,半径为1r =.圆()2231x y -+=的圆心为2(3,0)F ,半径为21r =,由圆的对称性可得1111||PF r PM PF r -+∣ ,2222||PF r PN PF r -≤≤+,所以1122||||5PM PN PF r PF r -≤+-+=|PM |-|PN |的最大值为5故答案为:530.(2022·黑龙江·哈九中高二期中)已知双曲线的方程为2214y x -=,如图所示,点()A ,B是圆(221x y +=上的点,点C 为其圆心,点M 在双曲线的右支上,则MA MB +的最小值为______1.【解析】由双曲线2214y x -=,可得1,2a b ==,则c =如图所示,设点D 的坐标为,则点,A D 是双曲线的焦点,根据双曲线的定义,可得22-==MA MD a ,所以22+=++≥+MA MB MB MD BD ,又由B 是圆(221x y +-=上的点,圆的圆心为C ,半径为1r =,所以11BD CD ≥-=,所以21MA MB BD +≥++,当点,M B 在线段CD 上时,取得等号,即MA MB +1.1.31.(2022·北京·高二期中)已知点()2,0A -,()2,0B ,(C ,动点M 到A 的距离比到B 的距离多2,则动点M 到B ,C 两点的距离之和的最小值为___________.【答案】4【解析】点()2,0A -,()2,0B ,且动点M 到A 的距离比到B 的距离多2,所以24MA MB AB -=<=,故动点M 的轨迹为双曲线右侧一支,则动点M 到B ,C 两点的距离之和2224MB MC MA MC AC +=+-≥-==,当且仅当M ,A ,C 三点共线时取等号,所以动点M 到B ,C 两点的距离之和的最小值为4.故答案为:4.32.(2022·湖南·嘉禾县第一中学高二阶段练习)过双曲线2218y x -=的右支上的一点P 分别向圆221:(3)4C x y ++=和圆222:(3)1C x y -+=作切线,切点分别为M ,N ,则22||||PM PN -的最小值为()A .8B .9C .10D .11【答案】B【解析】设双曲线的左、右焦点分别为12,F F ,()()2222221212||||413PM PN PF PF PF PF -=---=--()()()121212323PF PF PFPF PF PF =+--=+-()222223414219PF PF =+-=+≥⨯+=.故选:B33.(2022·四川省江油市第一中学高二期中(文))已知12F F ,为双曲线222:1(0)16x yC a a -=>的左、右焦点,点A 在双曲线的右支上,点(72)P ,是平面内一定点.若对任意实数m ,直线430x y m ++=与双曲线C 的渐近线平行,则2AP AF +的最小值为()A .6B .10-C .8D .2【答案】A【解析】∵双曲线C :()2221016x y a a -=>,∴双曲线的渐近线方程为4y x a =±,∵对任意实数m ,直线430x y m ++=与双曲线C 的渐近线平行,∴直线430x y m ++=与双曲线的渐近线方程为4y x a=±平行,∴3a =,∴5c =,∴1F 为()5,0-,∵()7,2P ,∴1PF ==∴211666AP AF AP AF PF +=+-≥-=,∴2AP AF +的最小值为6.故选:A.34.(2022·吉林市田家炳高级中学高二期中)设F 是双曲线221412x y -=的左焦点,()1,4A ,P 是双曲线右支上的动点,则PF PA +的最小值为()A .5B .5+C .7D .9【答案】D【解析】由双曲线221412x y -=,可知24a =,212b =,则22216c a b =+=,所以2a =,4c =,()1,4A 点在双曲线的两支之间,且双曲线右焦点为()4,0F ',由于P 是双曲线右支上的动点,∴由双曲线定义可得,24PF PF a '-==,而5PA PF AF ''+≥==,两式相加得9PF PA +≥,当且仅当A 、P 、F '三点共线时等号成立,则PF PA +的最小值为9.故选:D .35.(2022·江西南昌·高二期中(理))设(),P x y 是双曲线22154x y -=的右支上的点,则代数)AB .CD 3【答案】B设()()0,1,3,0A F ,上式表示PA PF -,由于双曲线22154x y-=的左焦点为()()3,0,3,0F F '-,双曲线的实轴2a =, 2PF PF a PF ''=-=-()2525PA PF PA PF PF PA ''-=-+=--+223110PF PA AF ''-≤=+当P 在F A '的延长线与双曲线右支的交点处时取到等号,所以()25PA PF PF PA '-=--+510故选:B考点6:离心率的值及取值范围36.(2022·广东·汕头市潮南区陈店实验学校高二阶段练习)已知0a b >>,1F ,2F ,是双曲线22122:1x y C a b-=的两个焦点,若点Р为椭圆22222:1x y C a b +=上的动点,当P 为椭圆的短轴端点时,12F PF ∠取最小值,则椭圆2C 离心率的取值范围为()A .22⎛ ⎝⎦B .2⎫⎪⎪⎣⎭C .20,3⎛ ⎝⎦D .23⎫⎪⎢⎪⎣⎭【答案】A【解析】假设点P 在x 轴上方,设()cos ,sin P a b θθ,则()0,πθ∈,由已知得()221F a b +,)222,0F a b +,设直线1PF 的倾斜角为α,直线2PF 的倾斜角为β,∴122sin tan cos PF k a a b αθ==++,222sin tan cos PF k a a b βθ==-+,∴()12tan tan F PF βα∠=-tan tan 1tan tan βααβ-=+()222sin b a b θ+=+-()222222sin sin b a b b a b θθ+=+-()222222sin sin b a b a b θθ=-⎡⎤⎢⎥--+⎢⎥⎢⎥⎢⎥⎣⎦考虑对勾函数()222sin 0sin 1sin b a b y θθθ-=+<≤,由于P 为椭圆的短轴端点时,π2θ=,12F PF ∠取最小值,即12tan F PF ∠取最小值,()222sin 0sin 1sin b a b y θθθ-=+<≤也取最小值,此时sin 1θ=,∵函数在⎛ ⎝上单调递减,∴1≤222a b ≤,解得202e <≤.即椭圆2C离心率的取值范围为2⎛ ⎝⎦.故选:A .37.(2022·四川省仁寿县文宫中学高二阶段练习(文))已知1F ,2F 是双曲线22221x y a b-=(0a >,0b >)的左、右焦点,点1F 关于渐近线的对称点恰好落在以2F 为圆心,2OF 为半径的圆上,则该双曲线的离心率为()ABC .2D1【答案】C【解析】由题意,F 1(−c ,0),F 2(c ,0),设一条渐近线方程为y =b a x ,则F 1b =.设F 1关于渐近线的对称点为M ,F 1M 与渐近线交于A ,∴|MF 1|=2b ,A 为F 1M 的中点,又O 是F 1F 2的中点,∴OA ∥F 2M ,∴∠F 1MF 2为直角,∴△MF 1F 2为直角三角形,∴由勾股定理得4c 2=c 2+4b 2∴3c 2=4(c 2−a 2),∴c 2=4a 2,∴c =2a ,∴e =2.故选:C38.(2022·福建·泉州市城东中学高二期中)已知双曲线2222:1(0,0)x y C a b a b-=>>的右顶点为A ,若以点A 为圆心,以b 为半径的圆与C 的一条渐近线交于M ,N 两点,且2OM ON =,则C 的离心率为()A .43BC.3D.2【答案】C【解析】过点A 作AP MN ⊥于点P ,则点P 为线段MN的中点,因为点A 为(,0)a ,渐近线方程为by a=±,所以点A 到渐近线b y x a =的距离为||=ab AP c ,在Rt OAP △中,2||==a OP c ,在Rt NPA中,2||===b NP c ,因为2OM ON =,所以||||||2||||3||=+=+=OP ON NP NP NP NP ,所以223=⨯a b c c,即223a b =,所以离心率e 3==c a .故A ,B ,D 错误.故选:C .39.(2022·江西省万载中学高二阶段练习(理))已知双曲线两条渐近线的夹角为60°,则该双曲线的离心率为()A .2BC .2D .12【答案】C【解析】由题设,渐近线与x 轴夹角θ可能为30°或60°,当30θ=︒,则tan 303b a =︒=,故e =;当60θ=︒,则tan 60ba=︒=2e =;所以双曲线的离心率为2故选:C40.(2022·福建·厦门外国语学校高二期末)如图所示,1F ,2F 是双曲线C :22221()00a x y a b b >-=>,的左、右焦点,过1F 的直线与C 的左、右两支分别交于A ,B 两点.若22345AB BF AF =∶∶∶∶,则双曲线的离心率为()A .2BCD【答案】C 【解析】22345AB BF AF =::::,不妨令3AB =,24BF =,25AF =,22222||||AB BF AF +=,290ABF ∠∴=,又由双曲线的定义得:122BF BF a -=,212AF AF a -=,11345AF AF ∴+-=-,13AF ∴=.123342BF BF a ∴-=+-=,1a \=.在12Rt BF F 中,222221212||||6452F F BF BF =+=+=,又2212||4F F c =,2452c ∴=,c ∴∴双曲线的离心率c e a=.故选;C41.(2022·广东汕头·高二期末)已知双曲线22221x y a b-=(a 、b 均为正数)的两条渐近线与直线1x =-)ABC .D .2【答案】D【解析】双曲线的渐近线为by x a=±,令1x =-,可得b y a=,不妨令1,b A a ⎛⎫- ⎪⎝⎭,1,b B a ⎛⎫-- ⎪⎝⎭,所以2bAB a=,所以12AOBA S AB x =⋅=AB ∴=,即2ba =b a=所以2c e a ==;故选:D42.(2022·湖北·鄂州市教学研究室高二期末)已知1F ,2F 分别是双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点,以12F F 为直径的圆与双曲线C 有一个交点P ,设12PF F △的面积为S ,若()21212PF PF S +=,则双曲线C 的离心率为()A .2B .2C D .【答案】C【解析】依题意,12PF PF ⊥,令1(,0)F c -,2(,0)F c ,则有22221212||||||4PF PF FF c +==,由212||(12||)PF PF S +=得:21211222||2||||6||||||PF PF PF PF PF PF =++,即有212||||PF PF c =,而222221221214(||)||2||2||||||a PF PF PF PF PF c PF =-=+-=,所以ce a==故选:C43.(2022·安徽省临泉第一中学高二期末)已知双曲线()2222:10,0x y C a b a b-=>>的两个焦点分别为()1,0F c -,()2,0F c ,M 是双曲线C 上一点,若120MF MF ⋅=,2212OM OF c ⋅=,则双曲线C 的离心率为()A .3B .31+C .2D .21+【答案】B【解析】()()22121221111242OM OF MO F F MF MF MF MF c⎛⎫⋅=-⋅=-+⋅-= ⎪⎝⎭,则222122MF MF c -=,又因为120MF MF ⋅=,12MF MF ⊥,即222124MF MF c +=,所以13MF c =,2MF c =,所以1223a MF MF c c =-=-,则31e =+,故选:B.44.(2022·江西上饶·高二期末(文))已知双曲线2222:1(0,0)x y C a b a b -=>>的焦距为122,,c F F 为其左右两个焦点,直线l 经过点(0,)b 且与渐近线平行,若l 上存在第一象限的点P 满足122PF PF b -=,则双曲线C 离心率的取值范围为()A .(1,2)B .(2,3)C .(1,3)D .(2,)+∞【答案】A【解析】因为满足122PF PF b -=的所有点在以12,F F 为焦点,长轴长为2b ,短轴长为2222c b a -=的双曲线,即22221x y b a-=上.故若l 上存在第一象限的点P 满足122PF PF b -=,则双曲线22221x y b a -=与直线l 有交点即可.又直线:b l y x b a =±+,数形结合可得,当b a <或22221x y b a-=的经过一象限的渐近线的斜率a b b a >即可,两种情况均有2222a b c a >=-,故222c a <,故离心率(1,2)e ∈故选:A考点7:双曲线的简单几何性质问题45.(多选题)(2022·河北·衡水市第二中学高二期中)已知曲线C :221mx ny +=,则()A .若0m n =>,则曲线CB .若0m n >>,则曲线C 是椭圆,其焦点在y 轴上C .若曲线C过点(,⎛⎫⎪ ⎪⎝⎭,则C 是双曲线D .若0mn =,则曲线C 不表示任何图形【答案】BC【解析】对于A ,0m n =>时,曲线C 可化为221x y n+=A 错误;对于B ,0m n >>时,曲线C 可化为22111x y m n+=表示的是椭圆,而11 0m n<<,所以其焦点在y 轴上,故B 正确;对于C,将点(,3⎛⎫- ⎪ ⎪⎝⎭,代入曲线C :221mx ny +=,有2311512133m n m m n n ⎧+==⎧⎪⎪⇒⎨⎨+==-⎪⎪⎩⎩,0mn <,所以曲线C 是双曲线,故C 正确;对于D ,若1m =,0n =,满足条件,此时曲线C :21x =,表示两条直线,故D 错误,故选:BC.46.(多选题)(2022·江苏连云港·高二期中)关于,x y 的方程2222126x y m m+=+-(其中26m ≠)表示的曲线可能是()A .焦点在y 轴上的双曲线B .圆心为坐标原点的圆C .焦点在x 轴上的双曲线D.长轴长为【答案】BC【解析】()()2222622m m m +--=-,当m =22264m m +=-=,此时2222126x y m m +=+-表示圆,故B 正确.当m <<22620m m ->+>,故2222126x y m m+=+-表示焦点在y 轴上的椭圆,若此时长轴长为268m -=即22m =-,矛盾,故D 错误.若m <m >260m -<,故2222126x y m m +=+-表示焦点在x 轴上的双曲线,故A 错误,C 正确.若m <<m <<22260m m +>->,故方程2222126x y m m+=+-表示焦点在x 轴上的椭圆,若长轴长为228m +=即m =,矛盾,故D 错误.故选:BC.47.(多选题)(2022·河北省曲阳县第一高级中学高二期中)若方程22131x y t t +=--所表示的曲线为C ,则下面四个选项中正确的是()A .若13t <<,则曲线C 为椭圆B .若曲线C 为椭圆,且长轴在y 轴上,则23t <<C .若曲线C 为双曲线,则3t >或1t <D .曲线C 可能是圆.【答案】BCD【解析】A.若方程22131x y t t +=--表示椭圆,则301031t t t t ->⎧⎪->⎨⎪-≠-⎩,解得13t <<且2t ≠,故错误;B.若曲线C 为椭圆,且长轴在y 轴上,则301031t t t t ->⎧⎪->⎨⎪-<-⎩,解得23t <<,故正确;C.若曲线C 为双曲线,则()()310t t --<,解得3t >或1t <,故正确;D.曲线C 是圆,则301031t t t t ->⎧⎪->⎨⎪-=-⎩,解得2t =,故正确;故选:BCD48.(多选题)(2022·云南·罗平县第一中学高二开学考试)已知曲线22:124x y C m m+=+-,则()A .当2m =时,则C的焦点是)1F,()2F B .当6m =时,则C 的渐近线方程为12y x =±C .当C 表示双曲线时,则m 的取值范围为2m <-D .存在m ,使C 表示圆【答案】ABD【解析】对于A ,当2m =时,曲线22:142x y C +=,则C 的焦点是)1F ,()2F ,所以A 正确;对于B ,当6m =时,曲线22:182x y C -=,则C 的渐近线方程为12y x =±,所以B 正确;对于C ,当C 表示双曲线时,()()240m m +-<,解得:4m >或2m <-,所以C 不正确;对于D ,当24m m +=-,即1m =时,曲线C 表示圆,所以D 正确.故选:ABD.49.(多选题)(2022·江苏江苏·高二期中)已知双曲线C :2213x y -=,则()A .双曲线C 的焦距为4B .双曲线C 的两条渐近线方程为:y =C .双曲线C 的离心率为3D .双曲线C 有且仅有两条过点()1,0Q 的切线【答案】ABD【解析】由双曲线标准方程得a =1b =,所以2c ==,焦距为4,A 正确;b a ==y =,B 正确;离心率为3c e a ===,C 错误;设过(1,0)Q 的直线的方程为(1)y k x =-,代入双曲线方程得:2222(13)6(33)0k x k x k -+-+=(*),2130k -=,即3k =±时,方程(*)只有一解,此时直线与渐近线平行,与双曲线相交,又由422364(13)(33)0k k k ∆=+-+=得2k =±,此时方程(*)有两个相等的实数解,此时直线与双曲线相切,即相切的直线有两条,D 正确.故选:ABD .50.(多选题)(2022·黑龙江·哈师大附中高二开学考试)双曲线的标准方程为2213y x -=,则下列说法正确的是()A .该曲线两顶点的距离为B .该曲线与双曲线2213x y -=有相同的渐近线C .该曲线上的点到右焦点的距离的最小值为1D .该曲线与直线l :)2y x =-,有且仅有一个公共点【答案】CD【解析】由已知双曲线中1,a b =2c =,顶点为(1,0)和(1,0)-,距离为2,A 错;该双曲线的渐近线方程是y =,而双曲线2213x y -=的渐近线方程是y =,不相同,B 错;该双曲线上的点到焦点的距离的最小值为1c a -=,C 正确;直线l 与该双曲线的一条渐近线平行,与双曲线有且只有一个公共点,D 正确,故选:CD .51.(2022·上海市新场中学高二期中)当0ab <时,方程22ax ay b -=所表示的曲线是()A .焦点在x 轴的椭圆B .焦点在x 轴的双曲线C .焦点在y 轴的椭圆D .焦点在y 轴的双曲线【答案】D【解析】当ab <0时,方程22ax ay b -=化简得221y x b ba a-=--,∴方程表示双曲线.焦点坐标在y 轴上;故选:D .考点8:利用第一定义求解轨迹52.(2022·河南·濮阳一高高二期中(理))若双曲线C 的方程为22145x y -=,记双曲线C 的左、右顶点为A ,B .弦PQ ⊥x 轴,记直线PA 与直线QB 交点为M ,其轨迹为曲线T ,则曲线T 的离心率为________.【解析】设P (0x ,0y ),则Q (0x ,-0y ),设点M (x ,y ),又A (-2,0),B (2,0),所以直线PA 的方程为00(2)2y y x x =++①,直线QB 的方程为00(2)2y y x x -=--②.由①得0022y yx x =++,由②得0022y y x x =---,上述两个等式相乘可得22022044y y x x =---,∵P (0x ,0y )在双曲线22145x y -=上,∴2200145x y -=,可得2200454y x -=,∴2020544y x =-∴22544y x =--,化简可得22145x y +=,即曲线T 的方程为22145x y +=53.(2022·吉林·白城一中高二期中)已知ABC 的两个顶点A B ,分别为椭圆2255x y +=的左焦点和右焦点,且三个内角A B C ,,满足关系式1sin sin sin 2B AC -=.(1)求线段AB 的长度;(2)求顶点C 的轨迹方程.【解析】(1)椭圆的方程为2255x y +=∴椭圆的方程为2215x y +=222=514a b c ∴==,,2c ∴=A B ,分别为椭圆2215x y +=的左焦点和右焦点,()()2,02,0A B ∴-,=4AB ∴∴线段AB的长度4(2)ABC 中根据正弦定理得:=2sin sin sin AB BC ACR C A B==(R 为ABC 外接圆半径),sin =,sin 222BC AC ABA B C R R R∴==1sin sin sin 2B A C -=12222AC BC AB R R R∴-=⨯1242AC BC AB AB ∴-==<=∴C 点的轨迹是以A B ,为左右焦点的双曲线的右支,且22AC BC a -==,=4=2AB c=12a c ∴=,,2223b c a =-=,∴顶点C 的轨迹方程为()22113yx x -=>54.(2022·全国·高二专题练习)如图所示,已知定圆1F :()2251x y ++=,定圆2F :()22516x y -+=,动圆M 与定圆1F ,2F 都外切,求动圆圆心M的轨迹方程.【解析】圆1F :()2251x y ++=,圆心()15,0F -,半径11r =;圆2F :()22516x y -+=,圆心()25,0F ,半径24r =.设动圆M 的半径为R ,则有11=+MF R ,24=+MF R ,∴2112310MF MF F F -=<=.∴点M 的轨迹是以1F ,2F 为焦点的双曲线的左支,且32a =,5c =,于是222914b c a =-=.∴动圆圆心M 的轨迹方程为2231991244≤-⎛⎫-= ⎪⎝⎭x y x .55.(2022·福建·厦门一中高二期中)已知动圆M 与圆221:(4)4C x y ++=外切与圆222:(4)4C x y -+=内切,则动圆圆心M 的轨迹C 的方程为___________.【答案】()2212412x y x -=≥【解析】设动圆圆心(),M x y ,半径为r ,因为圆M 与圆221:(4)4C x y ++=外切与圆222:(4)4C x y -+=内切,圆心()()124,0,4,0C C -,12||8C C =,所以1222MC r MC r ⎧=+⎪⎨=-⎪⎩,则12||||48MC MC -=<,于是点M 的轨迹是以点12,C C 为焦点的双曲线的右支.由题意,224,282,4,12a c a c b ==⇒===,于是,C 的方程为:()2212412x y x -=≥.故答案为:()2212412x y x -=≥.56.(2022·上海市新场中学高二期中)已知两点()(),3,03,0A B -,若4PA PB -=±,那么P 点的轨迹方程是______.【答案】22145x y -=【解析】设P 点的坐标为(),x y 因为44PA PB PA PB -=±⇒-=所以P 点的轨迹为焦点在x 轴的双曲线且3,242c a a ==⇒=所以b ==所以P 点的轨迹方程为:22145x y -=故答案为:22145x y -=57.(2022·吉林一中高二期中)若动圆过定点A ()3,0-且和定圆C :()2234x y -+=外切,则动圆圆心P 的轨迹方程是_________.【答案】2218y x -=()1x ≤-【解析】定圆的圆心为C()3,0,与A ()3,0-关于原点对称,设动圆P 的半径为r ,则有PA r =,因为两圆外切,所以2=+PC r ,即26PC PA AC -=<=,所以点P 的轨迹是以A ,C 为焦点的双曲线的左支,则1a =,3c =,2228b c a =-=,所以轨迹方程为2218y x -=()1x ≤-故答案为:2218y x -=()1x ≤-58.(2022·广东·深圳市宝安中学(集团)高二期中)已知点(3,0),(3,0),(1,0)M N B -,动圆C 与直线MN 相切于点B ,过M ,N 与圆C 相切的两直线相交于点P ,则点P 的轨迹方程为()A .221(1)8y x x -=>B .221(1)8y x x -=<-C .221(0)8y x x +=>D .221(1)10y x x -=>【答案】A【解析】设直线PM ,PN 与圆C 相切的切点分别为点Q ,T,如图,由切线长定理知,MB =MQ ,PQ =PT ,NB =NT ,于是有|PM|-|PN|=|MQ|-|NT|=|MB|-|NB|=2<6=|MN|,则点P 的轨迹是以M ,N 为左右焦点,实轴长2a =2的双曲线右支,虚半轴长b 有22238b a =-=,所以点P 的轨迹方程为221(1)8y x x -=>.故选:A59.(2022·江苏省镇江中学高二期中)动圆M 与圆1C :()2241x y ++=,圆2C :22870x y x +-+=,都外切,则动圆圆心M 的轨迹方程为()A .22115x y +=B .22115y x -=C .()221115y x x -=≥D .()221115y x x -=≤-【答案】D【解析】圆1C :()2241x y ++=,圆心()14,0C -,半径11r =.圆2C :()222287049x y x x y +-+=⇒-+=,圆心()24,0C ,半径23r =.设(),M x y ,半径为r ,因为动圆M 与圆1C ,2C 都外切,所以121122123MC r MC MC C C MC r ⎧=+⎪⇒-=<⎨=+⎪⎩,所以M 的轨迹为以12,C C 为焦点,22a =的双曲线左支.所以1a =,4c =,解得b =即M 的轨迹方程为:()221115y x x -=≤-.故选:D60.(2022·新疆·博尔塔拉蒙古自治州蒙古中学高二期中)动点P 到点(1,0)M 及点(3,0)N 的距离之差为2,则点P 的轨迹是()A .双曲线B .双曲线的一支C .两条射线D .一条射线【答案】D。

大招17 双曲线焦点三角形内切圆问题 大招总结双曲线焦点三角形的内切圆与12F F 相切于实轴顶点;且当P 点在双曲线左支时,切点为左顶点,且当P 点在双曲线右支时,切点为右顶点.证明:设双曲线22221x y a b-=的焦点三角形的内切圆且三边1212,,F F PF PF 于点,,A B C ,双曲线的两个顶点为12,A A||121212||PF PF CF BF AF AF -=-=-12122,2PF PF a AF AF a -=∴-=,A ∴在双曲线上,又A 在12F F 上, A 是双曲线与x 轴的交点即点12,A A椭圆焦点三角形的旁切圆与12F F 所在直线相切与顶点,当P 点位于左侧时,旁切圆在左侧切点是左顶点,在右侧时候,切点是右顶点证明:22,MP NP F N AF ==11112222F M F A F P F F PN NF a c ∴+=+++=+11F M F A a c ∴==+因此A 为切点典型例题例1.双曲线221169x y -=的左、右焦点分别12,F F P 、为双曲线右支上的点,12PF F 的内切圆与x 轴相切于点C ,则圆心I 到y 轴的距离为() A.1 B.2 C.3 D.4解:设三角形内切圆的切点为,,A B C ,其中C 在X 轴上,那么2121F C FC F A F B -=-,又AP PB =所以212121212F C FC F A F B F A AP F B BP F P F P a -=-=+--=-= 8=,又211210F C FC F F +== 所以C 点的横坐标为4,I 点的横坐标也为4, 故圆心I 到y 轴的距离为4.故选D.例2.已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为12,,F F e 为双曲线的离心率,P 是双曲线右支上的点,12PF F 的内切圆的圆心为I ,过2F 作直线PI 的垂线,垂足为B ,则点B 的轨迹是() A.椭圆 B.圆 C.抛物线 D.双曲线解:()()12,0,,0F c F c -,内切圆与x 轴的切点是点A ,122PF PF a -=,及圆的切线长定理知, 122AF AF a -=,设内切圆的圆心横坐标为x ,则()()2x c c x a +--= x a ∴=;OA a =,在2PCF 中,由题意得,2F B PI ⊥于B ,延长交12F F 于点C ,利用2ΔPCB PF B ≅,可知2PC PF =,∴在三角形12F CF 中,有:()()111211112.2222OB CF PF PC PF PF a a ==-=-=⨯=即点B 的轨迹是以O 为圆心,半径为a 的圆, 故选B.例3.已知(P 在双曲线22214x y b-=上,其左、右焦点分别为12F F 、,三角形12PF F 的内切圆切x 轴于点M ,则2MP MF ⋅的值为()A.1B.1C.2D.解:(P 在双曲线22214x y b -=上,可得b =()()123,0,3,0F F ∴-,如图,设(),0M x ,内切圆与x 轴的切点是点12,M PF PF 、与内切圆的切点分由双曲线的定义可得1224PF PF a -==,由圆的切线长定理知,PN PH =,故124NF HF -=,即124MF HF -=,设内切圆的圆心横坐标为x ,则点M 的横坐标为x , 故()()334,2x x x +--=∴=.(()2232,02MP MF ∴⋅=⋅-=,故选C.例4.点P 是双曲线22221x y a b-=右支上一点,12F F 、分别为左、右焦点.12PF F 的内切圆与x 轴相切于点N .若点N 为线段2OF 中点,则双曲线离心率为()1 B.2D.3 解:12PF F 的内切圆与x 轴相切于点.N ,设切点分别为,,N A B ,并设1122,,PA PB x BF NF y AF NF z ======,根据双曲线的定义122PF PF a -=,()()2,2x y x z a y z c ∴+-+=+=,解得z c a =-,点N 为线段2OF 中点,11,22z c c c a ∴=∴=-,2,2c a e ∴=∴=.故选B.自我检测1.椭圆2212:1(0)x C y a a +=>与双曲线2222:1(0)x C y m m-=>有公共焦点,左右焦点分别为12,F F ,曲线12,C C 在第一象限交于点,P I 是12PF F 内切圆圆心,O 为坐标原点,2F H 垂直射线PI 于H 点,OH =则I 点坐标是.解:由题意,122PF PF m m -===椭圆2212:1(0)x C y a a +=>与双曲线2222:1(0)x C y m m-=>有公共焦点,2211a m ∴-=+2a ∴=∴椭圆方程为2214x y +=,双曲线方程为2212x y -=联立方程可得P ⎝⎭设内切圆的半径为r ,圆心坐标为(),x r ,则由等面积可得(11422r ⨯=⨯+,2r ∴=-2PF的方程为y x =∴由I到直线的距离等于2-可得x =∴圆心坐标为.故答案为:2.已知点P 是双曲线()222210,0x y a b a b-=>>左支上除顶点外的一点,12,F F 分别是双曲线的左、右焦点,1221,PF F PF F ∠α∠β==,双曲线离心率为e ,则tan2tan2aβ=() A.11e e -+ B.11e e +- C.22e 1e 1+- D.22e 1e 1-+解:依题意,在12PF F 中,由正弦定理得:()2121sin sin sin 180PF PF F F αβαβ==⎡⎤-+⎣⎦与合比定理得:()2121sin sin sin 180F F PF PF βααβ-=--⎡⎤-+⎣⎦,即()22sin sin sin c a αβαβ=+-,2sincossinsincoscossintantansin()222222222sin sin 2cos sin sin sin cos cos sin tan tan 222222222c e a αβαβαβαβαβαβαβαβαβαβαβαβαβαβ+++++-======+-----tan112tantan ,.2121tan 2e e e e ααββ++∴=⋅∴=-- 故选B.3.已知双曲线22221(0,0)x y a b a b-=>>的左右焦点分别为1F 和2F 点O 为双曲线的中心,点P 在双曲线的右支上,12PF F 内切圆的圆心为Q ,圆Q 与x 轴相切于点A ,过2F 作直线PQ 的垂线,垂足为B ,则下列结论成立的是()A.OA OB >B.OA OB =C.OA OB <D.OA 与OB 大小关系不确定易知:121221211111,2222IF F PF F IF F PF F ∠∠α∠∠β====1212tan121tan2IAF A F A a c e IA F A c a e F Aαβ++====-- 3.解:()()12,0,,0F c F c -,内切圆与x 轴的切点是点A122PF PF a -=,及圆的切线长定理知, 122AF AF a -=,设内切圆的圆心横坐标为x ,则()()2x c c x a +--=x a ∴=;即OA a =,在三角形2PCF 中,由题意得,它是一个等腰三角形,2PC PF =,∴在三角形12F CF 中,有:()()111211112.2222OB CF PF PC PF PF a a ==-=-=⨯=OB OA ∴=.故选B.4.已知12,F F 分别为双曲线22221(0,0)x y a b a b-=>>的左、右焦点,点P 在双线线上且不与顶点重合,满足1221tan3tan22PF F PF F ∠∠=,该曲线的离心率为 .解:易知p 点在左支上,估12PF F 的内切圆I易得I 切12F F 于A 点1221tan3tan22PF F PF F ∠∠=121133IA IA F A AF c a c a∴=∴=⋅-+33422c a c a a c c a ∴+=-∴=∴=2e ∴=5.已知点P 为椭圆22221(0)x y a b a b+=>>上异于左、右顶点的任意一点,12,/2F F ~是左、右焦点,连接12,PF PF ,作12PF F 的旁切圆(与线段21,PF F P 延长线及12F F 延长线均相切),其圆心为O ',则动圆圆心O '的轨迹所在曲线是() A.直线 B.圆 C.椭圆 D.双曲线解:如图画出圆M ,切点分别为E D G 、、,由切线长相等定理知1122,,FG F E PD PE F D F G ===, 根据椭圆的定义知122PF PF a +=, ()1212PF PF F E DF PD PE ∴+=+=()1211FG F D FG F E =+= 122FG F G a =+=,22222,F G a c F G a c ∴=-=-,即点G 与点A 重合,∴点M 在x 轴上的射影是长轴端点,A M 点的轨迹是垂直于x 轴的一条直线(除去A 点);故选A.。

《圆锥曲线》 ---------双曲线主要知识点1、双曲线的定义 :(1)定义: _____________________________________________________________(2)数学符号: ________________________(3)应注意问题:2、双曲线的标准方程:图像标准方程不一样点同样点注意:怎样依据双曲线的标准方程判断出它的焦点在哪个轴上?进一步,怎样求出焦点坐标?3、双曲线的几何性质标准方程焦点焦距性范围极点质实轴虚轴对称性离心率渐近线注意:( 1)怎样比较标准地在直角坐标系中画出双曲线的图像?(2)双曲线的离心率的取值范围是什么?离心率有什么作用?(3)当a b时,双曲线有什么特色?4.双曲线的方程的求法(1)双曲线的方程与双曲线渐近线的关系①已知双曲线段的标准方程是x2y21 (a 0, b 0)x2y21(a 0, b 0) ),a2b2(或2a2b则渐近线方程为________________________________________________________________ ;②已知渐近线方程为 bx ay0 ,则双曲线的方程可表示为__________________________ 。
(2)待定系数法求双曲线的方程x2y21 有共同渐近线的双曲线的方程可表示为_______________________ ;①与双曲线b2a2②若双曲线的渐近线方程是y b_____________________ ;x ,则双曲线的方程可表示为ax2y21 共焦点的双曲线方程可表示为_______________________________ ;③与双曲线b2a2④过两个已知点的双曲线的标准方程可表示为______________________________________ ;x2y2⑤与椭圆a2b2 1 (a b 0) 有共同焦点的双曲线的方程可表示为______________________________________________________________________________ 。
典型例题一例1 求与双曲线191622=-y x 共渐近线且过()332-,A 点的双曲线方程及离心率. 解法一:双曲线191622=-y x 的渐近线方程为:x y 43±= (1)设所求双曲线方程为12222=-by a x∵43=a b ,∴a b 43= ① ∵()332-,A 在双曲线上 ∴191222=-ba ② 由①-②,得方程组无解(2)设双曲线方程为12222=-bx a y∵43=a b ,∴a b 34= ③ ∵()332-,A 在双曲线上,∴112922=-ba ④ 由③④得492=a ,42=b∴所求双曲线方程为:144922=-x y 且离心率35=e 解法二:设与双曲线191622=-y x 共渐近线的双曲线方程为:()091622≠=-λλy x ∵点()332-,A 在双曲线上,∴41991612-=-=λ ∴所求双曲线方程为:4191622-=-y x ,即144922=-x y . 说明:(1)很显然,解法二优于解法一.(2)不难证明与双曲线191622=-y x 共渐近线的双曲线方程()091622≠=-λλy x .一般地,在已知渐近线方程或与已知双曲线有相同渐近线的条件下,利用双曲线系方程()02222≠=-λλb y a x 求双曲线方程较为方便.通常是根据题设中的另一条件确定参数λ. (3)以上优美巧妙的解法,达到了化繁为易的目的.教学中,要引起重视.典型例题二例2 作方程21x y -=的图象.分析:∵21xy -=()()⎪⎩⎪⎨⎧>-≤-⇔111122x x x x∴方程图象应该是圆122=+y x 及双曲线122=-y x 在x 轴上方的图象.说明:在根据方程作出相应图象时,应遵循:“如果曲线C 的方程是()0=y x f ,,那么点()00y x P ,在曲线C 上的充要条件是()000=y x f ,”这一原则;另外,须注意方程变形的未知数的允许值可能会扩大,而原方程的曲线只能取原方程允许值范围内的那一部分.典型例题三例3 求以曲线0104222=--+x y x 和222-=x y 的交点与原点的连线为渐近线,且实轴长为12的双曲线的标准方程.分析:先求出渐近线方程,确定出其斜率,结合已知条件确定所求双曲线方程中的字母系数.解:∵⎪⎩⎪⎨⎧-==--+2201042222x y x y x ,∴⎩⎨⎧==23y x 或⎩⎨⎧-==23y x ,∴渐近线方程为x y 32±=当焦点在x 轴上时,由32=a b 且6=a ,得4=b . ∴所求双曲线方程为1163622=-y x 当焦点在y 轴上时,由32=b a ,且6=a ,得9=b . ∴所求双曲线方程为1813622=-x y 说明:(1)“定量”与“定位”是求双曲线标准方程的两个过程,解题过程中应准确把握.(2)为避免上述的“定位”讨论,我们可以用有相同渐近线的双曲线系方程去解,请读者自行完成.典型例题四例 4 已知双曲线的渐近线方程为023=±y x ,两条准线间的距离为131316,求双曲线标准方程.分析:可根据双曲线方程与渐近线方程的关系,设出双曲线方程,进而求出双曲线标准方程.解:∵双曲线渐近线方程为x y 32±=,∴设双曲线方程为()019422≠=-λλλy x (1)若0>λ,则λ42=a ,λ92=b∴准线方程为:λ131342±=±=c a x ,∴13131613138=λ,∴4=λ (2)若0<λ,则λ92-=a ,λ42-=b∴准线方程为:131392λ-±=±=c a y ,∴131316131318=-λ,∴8164-=λ ∴所求双曲线方程为:1361622=-y x 或12568164922=-x y 说明:(1)准确及进地应用有相同渐近线的双曲线系方程给我们的求解过程带来了方便. (2)通过待定系数法求出参数N .典型例题五例5 中心在原点,一个焦点为()01,F 的双曲线,其实轴长与虚轴长之比为m ,求双曲线标准方程.解:设双曲线的标准方程为12222=-b y a x ,则⎪⎩⎪⎨⎧===+mb ac b a 221222,解得⎪⎪⎩⎪⎪⎨⎧+=+=11122222m b m m a∴111122222=+-+m y m mx 为所求双曲线的标准方程. 说明:以上方法是求双曲线标准方程的通用方法,注意其中的运算技巧.典型例题六例6 求中心在原点,对称轴为坐标轴经过点()31-,P 且离心率为2的双曲线标准方程.解:设所求双曲线方程为:()0122≠=-k ky k x ,则()1312=--k k , ∴191=-kk ,∴8-=k ,∴所求双曲线方程为18822=-x y 说明:(1)以上巧妙简捷的设法是建立在一个事实的基础上的,即离心率2=e 是双曲线的等轴双曲线的充要条件,它的证明如下:设等轴双曲线()0222>=-m m y x ,则222m b a ==,∴22222m b a c =+=∴m c 2=,∴22===mm a c e 反之,如果一个双曲线的离心率2=e .∴2=ac,∴a c 2=,222a c =,∴2222a b a =+,∴22b a =,b a = ∴双曲线是等轴双曲线(2)还可以证明等轴双曲线的其他性质:两条渐近线互相垂直;等轴双曲线上任意一点到中心的距离是它到两个焦点的距离的比例中项等.典型例题七例7 已知点()03,A ,()02,F ,在双曲线1322=-y x 上求一点P ,使PF PA 21+的值最小.解:∵1=a ,3=b ,∴2=c ,∴2=e设点P 到与焦点()02,F 相应准线的距离为d 则2=dPF∴d PF =21,∴d PA PF PA +=+21至此,将问题转化成在双曲线上求一点P , 使P 到定点A 的距离与到准线距离和最小.即到定点A 的距离与准线距离和最小为直线PA 垂直于准线时,解之得,点⎪⎪⎭⎫⎝⎛2321,P .说明:灵活巧妙地运用双曲线的比值定义于解题中,将会带给我们意想不到的方便和简单.教学中应着重培养学生灵活运用知识的能力.典型例题八例8 已知:()11y x M ,是双曲线12222=-by a x 上一点.求:点M 到双曲线两焦点1F 、2F 的距离.分析:利用双曲线的第二定义.解:如图,设点M 到相应焦点1F 、2F 的准线的距离为1d 、2d .当M 点在双曲线的右支上时,a x ≥1,且有e d MF d MF ==2211∴a ex c a x e ed MF +=+==12111,a ex ca x e ed MF -=-==12122 当点M 在双曲线的左支上时,a x -≤1,且有e d MF d MF ==2211∴()a ex c a x e ed MF +-=+==12111,()a ex ca x e ed MF --=-==12122 说明:以上结论称为双曲线的焦点半径公式,它在解题过程中发挥着很大的优越性,可使解题过程的运算量简化,从而得到避繁就简效果.例如:在双曲线1121322-=-y x 的一支上有三个不同点()11y x A ,、()622,x B 、()33y x C ,与焦点()501,F 的距离成等差数列,求31y y +的值. 解:直接利用焦半径公式,得:a ey AF -=11,a e BF -=61,a ey CF -=31 ∴1112BF CF AF =+,∴()a e a y y e 212231-=-+,即1231=+y y注意:一般地,在涉及到双曲线上的点到焦点的距离问题,应用焦半径公式是一种简单快捷的方法.典型例题九例9 如图所示,已知梯形ABCD 中,CD AB 2=,点E 满足EC AE λ=,双曲线过C 、D 、E 三点,且以A 、B 为焦点,当4332≤≤λ时,求双曲线离心率的取值范围. 分析一:依题意,建立恰当的坐标系,并通过A 、B 、E 的坐标及双曲线的方程求解.解法一:以直线AB 为x 轴,以AB 的垂直平分线为y 轴,建立直角坐标系xOy ,则y CD ⊥轴,因双曲线过点C 、D ,且以A 、B 为焦点,由双曲线的对称性可知C 、D 关于y 轴对称.设()0,c A -、⎪⎭⎫ ⎝⎛h cC ,2、()00y x E ,,其中AB c 21=为双曲线的半焦距,h 是梯形的高.由λ=,即()⎪⎭⎫⎝⎛--=+00002y h x c y c x ,,λ,得()()λλ+-=1220c x ,λλ+=10h y 设双曲线方程为12222=-b y a x ,则离心率为a c e =.由点C 、E 在双曲线上,将C 、E 的坐标和ace =,代入双曲线方程得 由①得14222-=e b h ,将③代入②式中,整理得:()λλ214442+=-e ∴2312+-=e λ,又∵4332≤≤λ,∴43231322≤+-≤e ,∴107≤≤e ∴双曲线的离心率取值范围为[]107,.分析二:建立直线AC 方程,再与双曲线方程联立,借助一元二次方程根与系数关系解题.解法二:前面部分同解法一.可求得直线AC 方程为()c x chy +=32,将其代入双曲线方程222222b a y a x b =-中,得()()094849222222222222=+---c b a h a cx h a x h a c b又∵0x 、2c为上述二次方程的两根,∴()222222222094942c b h a c b a h a x c -+=⋅ ①又∵⎪⎭⎫ ⎝⎛h cC ,2在双曲线上,∴()44222-=e b h ②∵()()1220+-=λλc x ③将②③代入①中,得:()()()()2222222222294942122c c a b e a b a b e a c c ⋅--+-=⋅+-λλ ∵a c e =,∴2312+-=e λ 以下同解法一分析三:借助焦半径公式解题. ∵EC AE λ=,∴()()1220+-=λλc x ① ∴λλ+=1CAEA ,由焦半径公式,得:λλ+=⋅+--120c e a ex a ② 将①代入②,得:()()λλλλ+=⋅+⎥⎦⎤⎢⎣⎡+⋅-⋅--12122c e a c e a∵a c e =,∴2312+-=e λ 以下同解法一 说明:(1)此题的关键是:弄清应设定几个量之间关系(如:c 、h 、λ、e ).难点:如何自始至终保持思路清晰,有条不紊.(2)比较以上三种方法不难发现:解法二虽思路简单自然,但由于采取了联立方程消元的思想,也就导致了解题过程的运算繁琐,这对于学生的计算能力要求是很高的,解法三因巧妙地运用了焦半径公式,使得求解过程变得简洁快捷,而且给人以一种心满意足的感觉,这表明善于记忆一些中间结果对我们的学习帮助很大.典型例题十例10 设双曲线12222=-by a x )0(b a <<的半焦距为c ,直线l 过)0,(a 、),0(b 两点,且原点到直线l 的距离为c 43,求双曲线的离心率. 分析:由两点式得直线l 的方程,再由双曲线中a 、b 、c 的关系及原点到直线l 的距离建立等式,从而解出ac的值. 解:由l 过两点)0,(a ,),0(b ,得l 的方程为0=-+ab ay bx .由点到l 的距离为c 43,得c ba ab 4322=+.将22a cb -=代入,平方后整理,得0316)(1622222=+⋅-ca c a .令x c a =22,则0316162=+-x x .解得43=x 或41=x . 而a ce =,有x e 1=.故332=e 或2=e . 因b a <<0,故212222>+=+==ab a b a ac e ,所以应舍去332=e .故所求离心率2=e . 说明:此题易得出错误答案:2=e 或332=e .其原因是未注意到题设条件)0(b a <<,从而离心率2>e .而2332<,故应舍去. 典型例题十一例11 根据以下条件,分别求出双曲线的标准方程.(1)过点)2,3(-P ,离心率25=e . (2)已知双曲线的右准线为4=x ,右焦点为)0,10(F ,离心率2=e .(3)1F 、2F 是双曲线的左、右焦点,P 是双曲线上一点,且︒=∠6021PF F ,31221=∆F PF S ,又离心率为2.分析:(1)、(3)用待定系数法,(2)用定义法.解:(1)依题意,双曲线的实轴可能在x 轴上,也可能在y 轴上,分别讨论如下.如双曲线的实轴在x 轴上,设12222=-b y a x 为所求.由25=e ,得4522=a c . ①由点)2,3(-P 在双曲线上,得12922=-b a . ②又222c b a =+,由①、②得12=a ,412=b . ③ 若双曲线的实轴在y 轴上,设12222=-b y a x 为所求.同理有4522=a c ,19222=-ba ,222c b a =+.解之,得2172-=b (不合,舍去). ∴双曲线的实轴只能在x 轴上,所求双曲线方程为1422=-y x .(2)设双曲线上任意一点),(y x P ,因为双曲线右准线4=x ,右焦点)0,10(F ,离心率2=e ,根据双曲线的第二定义,有24)10(22=-+-x y x ,化简,得03612322=---x y x ,即14816)2(22=--y x . ∴所求双曲线方程为14816)2(22=--y x . (3)设双曲线方程为12222=-b y a x ,因c F F 221=,而2==ace ,由双曲线的定义,得c a PF PF ==-221.由余弦定理,得)60cos 1(2)(21221︒-⋅⋅+-=PF PF PF PF ,∴21224PF PF c c ⋅+=. 又31260sin 212121=︒⋅=∆PF PF S F PF , ∴4821=⋅PF PF .∴4832=c ,162=c ,得42=a ,122=b .∴所求双曲线的方程为112422=-y x .说明:对于本题(1)的解法,由于双曲线的焦点位置没有明确,若不分情况讨论,将会造成解法的片面性.对于题(2),容易造成以下三种误解:误解一:由10=c ,42==c a x ,得402=a ,则60222=-=a c b .故所求双曲线方程为1604022=-y x . 误解二:由焦点坐标)0,10(F ,知10=c .又2==ace ,得5=a .故7525100222=-=-=a c b .∴所求双曲线方程为1752522=-y x . 误解三:由2==a ce ,42=c a ,得8=a ,16=c ,则192222=-=a c b .故所求双曲线方程为11926422=-y x . 这三种误解的错因都是按双曲线中心在原点得出结论,造成遗漏题条件,从而导致错误的结果.题(3)虽属待定系数法,但要用到公式ab b a b a 2)(222+-=+和双曲线的定义,以及正弦定理、余弦定理等知识,具有较强的综合性.若在其中某个环节上出现错误,将无法得出正确结果.典型例题十二例11 在双曲线1131222=-x y 的一支上有三个点),(11y x A 、)6,(2x B 、),(33y x C 与焦点)5,0(F 的距离成等差数列.(1)求31y y +;(2)求证线段AC 的垂直平分线经过某个定点,并求出定点的坐标. 分析:利用双曲线的第二定义解(1),利用点差法结合(1)的结果证(2). 解:(1)依题意,得B 在双曲线上支上,故A 、B 、C 三点都在双曲线上支上,且上准线的方程为512=y . AF 、BF 、CF 成等差数列,根据双曲线的第二定义,得 )512(1)512(1)5126(231-+-=-y e y e e ,故1231=+y y .(2)由点A 、C 在双曲线上,故113122121=-xy ,113122323=-x y .两式相减,得013))((12))((31313131=-+--+x x x x y y y y .∴13)(13)(123131313131x x y y x x x x y y +=++=--.∴AC 的垂直平分线的斜率为3113x x +-.又AC 的中点坐标为)6,2(31x x +,故AC 的垂直平分线方程为 当0=x 时,225=y ,故AC 的垂直平分线过定点)225,0(.说明:1.本题属定值问题,存在的问题是一方面对定值的概念和求法弄不清楚,摸不出头绪;论另一方面不会运用式子的变换和曲线的定义.2.关于定值问题,一般通过计算证明其值与曲线的点的位置无关,或与直线的斜率无关.为了证明的目的更明确,可通过特殊情况,求出一个常数,猜想出这个定值.不同的设法,可以得到不同的证法.典型例题十三例13 已知双曲线12222=-by a x 的离心率21+>e ,左、右焦点分别为1F 、2F ,左准线为l ,能否在双曲线的左支上找到一点P ,使得1PF 是P 到l 的距离d 与2PF 的等比中项?分析:因题设中出现双曲线上点与焦点的距离,故可考虑用双曲线的第二定义解题.解:设在左半支上存在P 点,使d PF PF ⋅=221,由双曲线的第二定义,知e PF PF dPF ==121,即12PF e PF =. ①再由双曲线的第一定义,得a PF PF 212=-. ②由①、②,解得121-=e a PF ,122-=e aePF . 在21F PF ∆中,有c PF PF 221≥+, ∴c e aee a 21212≥-+-. ③利用ac e =,从③式得0122≤--e e . 解得2121+≤≤-e . 由1>e ,得211+≤<e ,与已知21+>e 矛盾.∴符合条件的点P 不存在. 说明:(1)解答探索性命题,一般可先设点P 存在,再利用已知条件探求.若得出矛盾,则说明P 点不存在;否则,便得到P 点的位置.(2) 211+≤<e 是双曲线12222=-by a x 左支上存在P 点,使d PF PF ⋅=221成立的充要条件.典型例题十四例14 直线1+=kx y 与双曲线122=-y x 的左支相交于A ,B 两点,设过点)0,2(-和AB 中点的直线l 在y 轴上的截距为b ,求b 的取值范围.分析:首先应写出直线l 的方程,因此需求出AB 的中点坐标,将直线1+=kx y 与双曲线方程122=-y x 联立,消去y 得到关于x 的一元二次方程,利用韦达定理可得到AB 中点的坐标表达式.解:由方程组⎩⎨⎧=-+=,1,122y x kx y 消去y 得 022)1(22=---kx x k . ①设),(11y x A 、),(22y x B ,AB 中点的坐标为),(00y x . ∵直线1+=kx y 与双曲线122=-y x 的左支相交于A ,B 两点, ∴方程①有两个不大于-1的不等实根.令22)1()(22---=kx x k x f ,则⎪⎪⎩⎪⎪⎨⎧≥-⋅-<->-+-=∆,0)1()1(,01,0)1(8)2(2222f k kk k k 解得21<<k ,222012k k x x x -=+=,200111kkx y -=+=.∴直线l 的方程是21201122+-+=---kkx k o y 令0=x ,得1617)41(122222+--=++-==k k k y b . ∵21<<k ,∴22-<b 或2>b .说明:(1)涉及直线与双曲线相交弦有关的参数范围的讨论问题,0>∆是必不可少的条件. (2)关于直线与双曲线的某一支的相交问题,不但要考虑0>∆,同时要考虑方程根的取值范围,以下以双曲线12222=-by a x )0,0(>>b a 为例作简单说明.⎪⎩⎪⎨⎧=-12222b y ax 直线方程关于x 的一元二次方程02=++s nx mx .①若直线与双曲线右支相交于不同两点,则其充要条件是⎪⎩⎪⎨⎧>>+>∆≠.0,0,002121x x x x m 且②若直线与双曲线左支相交于不同两点,则其充要条件是⎪⎩⎪⎨⎧><+>∆≠.0,0,002121x x x x m 且③若直线与双曲线不同两支交于两点,则其充要条件是⎩⎨⎧<>∆≠.0,0021x x m 且典型例题十五例15 已知1l ,2l 是过点)0,2(-P 的两条互相垂直的直线,且1l ,2l 与双曲线122=-x y 各有1A ,1B 和2A ,2B 两个交点.(1)求1l 的斜率1k 的取值范围;(2)若22115B A B A =,求1l ,2l 的方程; (3)若1A 恰是双曲线的一个顶点,求22B A 的值.分析:第(1)小题利用直线1l ,2l 与双曲线都有两个交点,从而可以转化为一元二次方程有两个不等实根,判别式大于零,由此可以得到1k 满足的不等式组;第(2)小题利用弦长公式求1k ,再由点斜式方程求出直线方程; 第(3)小题利用直线1l 过A 点求1k ,再由弦长公式求22B A .解:(1)依题意,直线1l ,2l 的斜率都存在,设1l 的方程为)2(1+=x k y )0(1≠k 直线2l 的方程为)2(2+=x k y )0(2≠k ,且121-=k k .由方程组⎪⎩⎪⎨⎧=-+=,1),2(221x y x k y 消去y ,整理得01222)1(2121221=-++-k x k x k ①若0121=-k ,则方程①只有一个解,即l 与双曲线只有一个交点,与题设矛盾. 故0121≠-k ,即11≠k .∵直线1l 与双曲线有两个不同交点,∴0)13(4)12)(1(4)22(2121212211>-=---=∆k k k k .由方程组⎪⎩⎪⎨⎧=-+=,1),2(222x y x k y 消去y ,整理得01222)1(2222222=-++-k x k x k ②同理0122≠-k ,0)13(4222>-=∆k .所以1l ,2l 与双曲线各有两个交点,等价于⎪⎪⎪⎩⎪⎪⎪⎨⎧-=≠≠>->-,1,1,1,013,01321212221k k k k k k解得⎪⎩⎪⎨⎧≠<<.1,33311k k∴)3,1()1,33()33,1()1,3(1Y Y Y ----∈k .(2)设),(111y x A ,),(221y x B ;由方程①可得122212121-=+k k x x ,112212121--=k k x x . ∴221212122121211)1()13)(1(4))(1(--+=-+=k k k x x k B A ③ 同理,由方程②可得2222222222)1()13)(1(4--+=k k k B A . ④ ∵121k k -=,代入④得 2212121222)1()3)(1(4k k k B A --+=. ⑤ 由22115B A B A =,得2222115B A B A =.将式③和式⑤代入得22121212212121)1()3)(1(45)1()13)(1(4k k k k k k --+⨯=--+.解得21±=k . 当21=k 时,)2(21+=x y l :,)2(222+-=x y l :; 当21-=k 时,)2(21+-=x y l :,)2(222+=x y l :. (3)双曲线122=-x y 的顶点为)1,0(,)1,0(-. 取)1,0(1A 时,有1)20(1=+k ,解得221=k ,于是2112-=-=k k .将22-=k 代入方程②得03242=++x x .设2l 与双曲线的两个交点),(332y x A ,),(442y x B ,则2443-=+x x ,343=x x .则24322222))(1(x x k B A -+=60]34)24[(32=⨯--=.∴15222=B A .当取)1,0(1-A 时,由双曲线关于x 轴对称,知15222=B A .说明:(1)直线与曲线的位置关系,可以通过讨论直线方程与曲线方程组成的方程组的实数解的个数来确定,通常消去方程组中变量y (或x )得到关于变量x (或y )的一元二次方程,考虑该一元二次方程的判别式∆,则有:⇔>∆0直线与双曲线相交于两个点; ⇔=∆0直线与双曲线相交于一个点; ⇔<∆0直线与双曲线无交点.若得到关于x (或y )的一元二次方程,则直线与双曲线相交于一个点,此时直线平行于双曲线的一条渐近线.(2)直线l 被双曲线截得的弦长2212))(1(x x k AB -+=或2212))(11(y y k-+,其中k 是直线l 的斜率,),(11y x ,),(22y x 是直线与双曲线的两个交点A ,B 的坐标,且212212214)()(x x x x x x -+=-,21x x +,21x x 可由韦达定理整体给出.典型例题十六例16 已知双曲线的渐近线方程是043=+y x ,043=-y x ,求双曲线的离心率. 分析:由渐近线的斜率与a ,b 的关系得到a ,c 的关系,从而求出e .解:(1)设双曲线方程为12222=-by a x )0,0(>>b a .∵渐近线方程为043=+y x ,043=-y x , ∴43=a b . 又∵1222222-=-==e aa c ab a b , ∴4312=-e .∴45=e .(2)设双曲线方程为12222=-bx a y )0,0(>>b a .∵渐近线方程为043=+y x ,043=-y x ,∴43=b a . ∵12-=e a b ,∴3412=-e ,35=e . ∴离心率45=e 或35=e .说明:(1)必须分两种情况求离心率,共渐近线的双曲线方程为:λ=-2222by a x )0(≠λ的形式,它们的渐近线为x aby ±=. (2)关于双曲线的渐近线,可作如下小结:若知双曲线方程为12222=-b y a x 或12222=-bx a y ,则它们的渐近线方程只需将常数“1”换成“0”,再写成直线方程的形式即可;若知双曲线的两渐近线,先写成一个方程即02222=-by a x 的形式,再设出双曲线方程λ=-2222by a x )0(≠λ; 实轴长焦矩长离心率=e ;若焦点在x 轴上,渐近线斜率为虚轴长比实轴长;若焦点在y 轴上,渐近线斜率为实轴长比虚轴长.典型例题十七例17 已知双曲线S 的两条渐近线过坐标原点,且与以)0,2(A 为圆心,1为半径的圆相切,双曲线S 的一个顶点'A 和A 关于直线x y =对称,设直线l 过点A ,斜率为k .(1)求双曲线S 的方程;(2)当1=k 时,在双曲线S 的上支求点B ,使其与直线l 的距离为2;(3)当10<≤k 时,若双曲线S 的上支上有且只有一个点B 到直线l 的距离为2,求斜率k 的值及相应的点B 的坐标.分析:本题考查的内容多,其中有直线与圆相切,关于直线x y =的对称点,双曲线的性质,点到直线的距离等等,如果采取各个击破的办法,那么问题便能解决.解:(1)由已知得双曲线的渐近线为x y ±=,因而S 为等轴双曲线,其中一个顶点为)2,0('A ,所以双曲线S 的方程为12222=-x y . (2)若)2,(2+x x B 是双曲线S 的上支上到直线2-=x y l :的距离为2的点,则22222=-+-x x ,解得2=x ,2=y .故B 点坐标为)2,2(.(3)因为当10<≤k 时,双曲线S 的上支在直线l 的上方,所以点B 在直线l 的上方.设直线'l 与直线)2(-=x k y l :平行,两线间的距离为2,直线'l 在直线l 的上方,双曲线S 的上支上有且只有一个点B 到直线l 的距离为2,等价于直线'l 与双曲线S 的上支有且只有一个公共点.设'l 的方程是m kx y +=,由l 上的点A 到'l 的距离为2,可知2122=++k m k ,解得)1(22k k m -+±=,其中)1(22k k m -+-=舍去.由方程222=-x y 及m kx y +=,消去y 得,022)1(222=-++-m mkx x k . ∵12≠k ,∴)123(8)22(4222+-=+-=∆k k k k m . 令0=∆.∵10<≤k ,解得0=k ,552=k . 当0=k 时,2=m ,解得0=x ,2=y ,∴点B 的坐标为)2,0(.当552=k 时,510=m ,解得22=x ,10=y ,∴点B 的坐标为)10,22(. 说明:若已知双曲线渐近线方程为0=±qy px ,则共渐近线的双曲线方程为λ=-2222p y q x ,其中λ为不等于零的常数,另外要善于把问题转化,(3)便是把原题转化为m kx y l +=:'与双曲线S 上支有且只有一个公共点问题.典型例题十八例18 如下图,给出定点)0,(a A )0(>a 和直线1-=x l :,B 是直线l 上的动点,BOA ∠的角平分线交AB 于C ,求点C 的轨迹方程,并讨论方程表示的曲线类型与a 值的关系.分析:根据曲线的条件求轨迹方程,是解析几何的手段.要认真分析角平分线这一重要条件,分清主动点与从动点的关系,综合利用所学知识求出C 点横坐标与纵坐标的关系.解:依题意,记),1(b B -,R b ∈,则直线OA 与OB 的方程分别为0=y 和bx y -=, 设C 点坐标为),(y x ,则有a x <≤0,由OC 平分AOB ∠,知点C 到OA 、OB 距离相等,根据点到直线的距离公式, 得:21bbx y y ++=①依题设,点C 在直线AB 上,故有)(1a x aby -+-=. 由0≠-a x ,得,ax ya b -+-=)1( ②将②式代入①式,得22222)1()()1(1⎥⎦⎤⎢⎣⎡-+-=⎥⎦⎤⎢⎣⎡-++a x xy a y a x y a y . 整理得:0])1(2)1[(222=++--y a ax x a y ,若0≠y ,则0)1(2)1(22=++--y a ax x a .)0(a x <<若0=y ,则0=b ,π=∠AOB ,点C 的坐标为)0,0(,满足上式. 综上,得点C 的轨迹方程为:0)1(2)1(22=++--y a ax x a )0(a x ≤≤ (1)当1=a 时,轨迹方程化为x y =2)10(<≤x ③ 此时,方程③表示抛物线弧段(2)当1≠a 时,轨迹方程为11)1()1(22222=-+---a a y a a a a x ,其中a x <≤0 ④∴当10<<a 时,方程④表示椭圆弧段,当1>a 时,方程④表示双曲线一支的弧段. 说明:本题求轨迹问题,要求考生有较高的能力和扎实的基本功,同时要求对问题考虑完整和有较强的运算能力.对字母系数a 的讨论是高考重点考查的内容.典型例题十九例19 已知双曲线C 的实轴在直线2=x 上,由点)4,4(-A 发出的三束光线射到x 轴上的点P 、Q 及坐标原点O 被x 轴反射,反射线恰好分别通过双曲线的左、右焦点1F 、2F 和双曲线的中心M .若4=PQ ,过右焦点的反射光线与右准线交点的纵坐标为98,求双曲线C 的方程和入射光线AP 、AQ 所在直线的方程.分析:光线反射的问题,实质上是寻找点关于直线的对称点的问题,而求双曲线方程,实质上是求双曲线中点),(k h M 与a 、b 的问题.解:依题意,设双曲线中心为)2,(h M ,又点A 关于x 轴的对称点为)4,4('--A ,所以直线O A '的方程为x y =,与2=y 联立,得2=h .设双曲线方程为1)2()2(2222=---b y a x ,焦点)2,2(1c F -,)2,2(2c F +,右准线c a x 22+=,从而1'F A 的方程为:)4(664+-=+x cy ,2'F A 的方程为:)4(664++=+x cy . 在上面两式中分别令0=y ,则P 点坐标为)0,32(c -,Q 点坐标为)0,32(c,再由4=PQ ,则3=c ,∴P 点坐标为)0,2(-,Q 点坐标为)0,2(.在)4(6642'++=+x c y F A :中,令98=y ,得310=x ,在31022=+c a 中,由3=c ,得42=a ,52=b ,所以,所求双曲线方程为15)2(4)2(22=---y x .直线AP 的方程为042=++y x ,直线AQ 的方程为0432=-+y x .说明:本题关键要掌握中心不在原点的双曲线的焦点坐标,准线方程的求法,通过逆向思维,求出x 轴上的点P 、Q 的坐标,从而使问题迎刃而解.。
第13讲椭圆、双曲线的两个斜率积结论知识与方法1.椭圆的第三定义:如图1所示,设椭圆2222:1x yCa b+=()0a b>>的左、右顶点分别为A和B,点P为椭圆C上不与A、B重合的动点,则直线PA、PB的斜率之积22 21PA PB bk k ea⋅=−=−.推广:如图2所示,A、B为椭圆2222:1x yCa b+=()0a b>>上关于原点对称的任意两点,P为椭圆C上的动点且直线PA、PB的斜率均存在,则直线PA、PB的斜率之积22 21PA PB bk k ea⋅=−=−2.椭圆中点弦结论:如图3所示,设AB是椭圆2222:1x yCa b+=()0a b>>的任意一条不垂直于坐标轴且不过原点的弦,M为AB的中点,则直线OM与直线AB的斜率之积22 21OM AB bk k ea⋅=−=−.3.双曲线的第三定义:如图4所示,设A、B分别为双曲线2222:1x yCa b−=()0,0a b>>的左、右顶点,P为双曲线上不同于A、B的任意一点,则直线PA、PB的斜率之积22 21PA PB bk k ea⋅==−推广:如图5所示,设A、B为双曲线2222:1x yCa b−=()0,0a b>>上关于原点O对称的任意两点,P为双曲线C上的动点,且PA、PB的斜率都存在,则直线PA、PB的斜率之积2221PA PBbk k ea⋅==−4.双曲线中点弦结论:如图6所示,设AB是双曲线2222:1x yCa b−=()0,0a b>>的不垂直于坐标轴且不过原点的弦,M为AB中点,则直线OM与直线AB的斜率之积22 21OM AB bk k ea⋅==−.提醒:若是焦点在y 轴上的椭圆或双曲线,则上述四个斜率积的结果都要取倒数.典型例题【例1】设椭圆22:12x C y +=的左、右顶点分别为A 和B ,P 为椭圆C 上不与A 、B 重合的任意一点,则直线PA 、PB 的斜率之积为______.【解析】由题意,()A,)B,设()00,P x y,0x ≠,则220012x y +=,所以22012x y =−,所以202022*******2PA PB x y k k x x −⋅====−−−.【答案】12−变式1 设椭圆2222:1x y C a b+=()0a b >>的左、右顶点分别为A 和B ,点P 为椭圆C 上一点且直线PA 、PB 的斜率之积为12−,则椭圆C 的离心率为______. 【解析】由题意,2112PA PB k k e ⋅=−=−,所以椭圆C的离心率2e =.变式2 设A 为椭圆2222:1x y C a b+=()0a b >>上第一象限的一点,B 与A 关于原点对称,点P 在椭圆C 上且直线PA 、PB 的斜率之积为12−,则椭圆C 的离心率为______. 【解析】由题意,可设()11,A x y ,则()11,B x y −−,且2211221x y a b +=,所以()222222111221x b y b x a a a ⎛⎫=−=−− ⎪⎝⎭,设()22,P x y ,则2222221x y a b +=,所以()222222222221x b y b x a a a ⎛⎫=−=−− ⎪⎝⎭,从而()()22222221222222121212222221212121PA PBb b x a x a a a y y y y y y b k k x x x x x x x x a ⎡⎤−−−−−⎢⎥−+−⎣⎦⋅=⋅===−−+−−, 由题意,2212b a −=−,所以222a b =,从而22222a ac =−,故椭圆C的离心率2c e a ==.【答案】2【反思】上面的求解过程其实就是椭圆第三定义推广结论的推导过程,熟悉了这一结论,小题中可直接根据21PA PB k k e ⋅=−求得离心率.变式3 椭圆22:12x C y +=的左、右顶点分别为A 和B ,点P 在C 上,设直线PA 、PB 的斜率分别为1k 、2k ,若112k ≤≤,则2k 的取值范围是______.【解析】由椭圆第三定义,1212k k =−,所以2112k k =−,111111*********k k k ≤≤⇒≤≤⇒−≤−≤−,故2k 的取值范围是11,24⎡⎤−−⎢⎥⎣⎦. 【答案】11,24⎡⎤−−⎢⎥⎣⎦【反思】看到椭圆左、右顶点与椭圆上另外一点的连线,想到椭圆第三定义的斜率积结论.变式4 已知椭圆2222:1x y C a b+=()0a b >>的左、右顶点分别为A 、B ,若椭圆C 上存在不与A 、B 重合的点P ,使得120APB =∠︒,则椭圆C 的离心率的取值范围是______.【解析】如图,不妨设P 在x 轴上方,120APB =∠︒,记PAB α∠=,PBA β∠=,则18060APB αβ+=︒−∠=︒,所以()tan tan tan 1tan tan αβαβαβ++==−从而)tan tan 1tan tan αβαβ+=−①,由椭圆第三定义,()2tan tan tan tan 1PA PB k k e απβαβ⋅=⋅−=−=−,所以2tan tan 1e αβ=−,代入①可得2tan tan αβ+=,显然α,β均为锐角, 所以tan 0α>,tan 0β>,2tan tan αβ=+≥= 当且仅当tan tan αβ=时取等号, 故42344e e ≥−,结合01e <<1e ≤<.【答案】⎫⎪⎪⎣⎭【例2】不与坐标轴垂直且不过原点O 的直线l 与椭圆22:12x C y +=相交于A 、B 两点,M为AB 的中点,则直线OM 与直线l 的斜率之积为______.【解析】设()11,A x y ,()22,B x y ,则221122221212x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩,两式作差得:2222121202x x y y −+−=,整理得:1212121212y y y y x x x x +−⋅=−+−,所以直线OM 与直线l 的斜率之积为12−.【答案】12−【反思】上面的求解过程是用点差法推导中点弦结论,熟悉结论之后,小题中可直接根据21OM AB k k e ⋅=−求得结果.变式1 直线l 与椭圆2222:1x y C a b+=()0a b >>相交于A 、B 两点,O 为原点,M 为AB 的中点,若直线OM 与直线l 的斜率之积为12−,则椭圆C 的离心率为______.【解析】由中点弦结论,2112OM AB k k e e ⋅=−=−⇒=.变式2 已知直线l 与椭圆22:12x C y +=相交于A 、B 两点,若AB 的中点为11,2M ⎛⎫⎪⎝⎭,则直线l 的方程为______.【解析】由中点弦结论,12OM AB k k ⋅=−,又AB 的中点为11,2M ⎛⎫ ⎪⎝⎭,所以12OM k =,故1AB k =−,显然M 在直线l 上,所以直线l 的方程为()112y x −=−−,化简得:2230x y +−= 【答案】2230x y +−=变式3 (2013·新课标Ⅰ卷)已知椭圆2222:1x y E a b+=()0a b >>的右焦点为()3,0F ,过点F 的直线交椭圆E 于A 、B 两点,若AB 的中点坐标为()1,1−,则E 的方程为( )A.2214536x y += B .2213627x y += C.2212718x y += D.221189x y += 【解析】如图,设AB 中点为M ,由中点弦结论,22AB OM b k k a⋅=−,由题意,1OM k =−,由图可知,()011312AB MF k k −−===−,所以()22112b a ⨯−=−,整理得:222a b =又椭圆E 的右焦点为()3,0F ,所以229a b −=, 故218a =,29b =,从而椭圆E 的方程为221189x y +=【答案】D【反思】看到椭圆的弦中点,联想到中点弦斜率积结论22AB OMb k k a⋅=−【例3】设P 是左、右顶点分别为A 、B 的双曲线221x y −=上的一点,若直线PA 的倾斜角为23π,则直线PB 的倾斜角为( ) A.6πB.34π C.56π D.1112π【解析】由题意,()1,0A −,()1,0B ,设()00,P x y ,则22001x y −=,所以22001y x =−,从而220000220000111111PA PBy y y x k k x x x x −⋅=⋅===+−−−, 直线PA的倾斜角为22tan 33PA k ππ⇒==所以13PB PA k k ==−,故直线PB 的倾斜角为56π. 【答案】C变式1 已知A 、B 、P 是双曲线22221x y a b−=()0,0a b >>上不同的三点,且A 、B 连线经过坐标原点,若直线PA 、PB 的斜率乘积为1,则该双曲线的离心率为______.【解析】由题意,可设()11,A x y ,()11,B x y −−,()22,P x y ,则2211221x y a b−=,所以()222222111221x b y b x a a a⎛⎫=−=− ⎪⎝⎭,同理,()2222222b y x a a =−,从而()()()22222222222212121222b b b y y x a x a x x a a a−=−−−=−,故222212121222212121PA PBy y y y y y b k k x x x x x x a −+−⋅=⋅==−+−,由题意,1PA PB k k ⋅=,所以221b a =,故b a =,不妨设1a b ==,则c =变式2 (2015·新课标Ⅱ卷)已知A 、B 是双曲线E 的左、右顶点,点M 在E 上,ABM为等腰三角形,且顶角为120°,则E 的离心率为( )B.2【解析】解法1:设双曲线2222:1x y E a b−=()0,0a b >>,如图,不妨设P 在第一象限,过M作MN x ⊥轴于N ,由题意,120ABM =∠︒,2AB BM a ==, 所以18060MBN ABM ∠=︒−∠=︒,从而cos60BN BM a =⋅︒=,sin 60AB BM =⋅︒=,故M 点的坐标为()2a ,代入双曲线方程得:())222221a ab−=,化简得:22a b =,所以222a c a =−,故离心率ce a==. 解法2:设双曲线2222:1x y E a b−=()0,0a b >>,由题意,120ABM =∠︒,30BAM BMA ∠=∠=︒,18060MBN ABM ∠=︒−∠=︒所以直线AM 和直线BM 的斜率分别为3和,由双曲线第三定义,211MA MB k k e ⋅===−,所以离心率e =【答案】D【例4】过点()1,2M 作斜率为12的直线与双曲线2222:1x y C a b−=()0,0a b >>相交于A 、B 两点,若M 点恰为弦AB 的中点,则双曲线C 的离心率为______.【解析】设()11,A x y ,()22,B x y ,则22112222222211x y a b x y a b ⎧−=⎪⎪⎨⎪−=⎪⎩,两式作差得:22221212220x x y y a b −−−=, 整理得:2121221212y y y y b x x x x a +−⋅=+−,即22122OM AB b k k a ⋅=⨯=,所以22a b =,从而222a c a =−,故ce a==.变式1 已知双曲线22:122x y C −=,过点()1,2M 的直线l 与双曲线C 交于A 、B 两点,若M恰好为AB 的中点,则直线l 的方程为______.【解析】设直线l 的斜率为k ,由中点弦结论,221OM b k k a⋅==,又点M 的坐标为()2,1,所以12OM k =,故2k =,显然直线l 过点M ,所以直线l 的方程为()122y x −=−,化简得:23y x =−【答案】23y x =−变式2 已知双曲线2222:1x y C a b−=()0,0a b >>的右焦点为()2,0F ,过点F 的直线交双曲线C 于A 、B 两点,若AB 中点为()1,3M −−,则双曲线C 的方程为______. 【解析】由中点弦结论,22303312OM ABb k k a−−⋅=⨯==−−,所以223b a =,又双曲线C 的右焦点为()2,0F ,所以224a b +=,从而21a =,23b =,故双曲线C 的方程为2213y x −= 【答案】2213y x −=强化训练1.(★★★)过点()1,1M −作斜率为13的直线与椭圆2222:1x y C a b+=()0a b >>相交于A 、B 两点,若M 是线段AB 的中点,则椭圆C 的离心率为______.【解析】用中点弦结论,21113AB OM k k e ⋅=−⨯=−,所以椭圆C的离心率e =.2.(★★★)已知椭圆22:162x y C +=的左、右顶点分别为A 和B ,P 为椭圆C 上不与A 、B重合的一点,若直线PA 的斜率的取值范围是[]1,2,则直线PB 的斜率的取值范围是______.【解析】设PA 、PB 的斜率分别为1k 、2k ,由椭圆第三定义,1213k k =−,所以2113k k =−,由题意,112k ≤≤,所以11112k ≤≤,故1111336k −≤−≤−,即直线PB 的斜率的取值范围是11,36⎡⎤−−⎢⎥⎣⎦【答案】11,36⎡⎤−−⎢⎥⎣⎦3.(★★★)已知双曲线2222:1x y C a b−=()0,0a b >>的离心率为2,A 、B 为双曲线C 的左、右顶点,P 为C 上不与A 、B 重合的一点,若直线PA 的斜率的取值范围是[]2,3,则直线PB 的斜率的取值范围是______.【解析】设PA 、PB 的斜率分别为1k 、2k ,由双曲线第三定义,21213k k e =−=,所以213k k =, 由题意,123k ≤≤,所以13312k ≤≤,故直线PB 的斜率的取值范围是31,2⎡⎤⎢⎥⎣⎦【答案】31,2⎡⎤⎢⎥⎣⎦4.(★★★)设P 是左、右顶点分别为A 、B 的双曲线2213y x −=上的一点,若直线PA 的斜率为1−,则直线PB 的斜率为______.【解析】由题意,1PA k =−,由双曲线第三定义,223PA PB b k k a ⋅==,所以33PB PAk k ==−.【答案】3−5.(★★★)设椭圆2222:1x y C a b+=()0a b >>上的A 和B 两点关于原点对称,点P 为椭圆C上一点且直线PA 、PB 的斜率之积为14−,则椭圆C 的离心率为______. 【解析】由椭圆第三定义的推广结论,2114PA PB k k e ⋅=−=−,所以椭圆C的离心率e =.6.(★★★)直线l 与椭圆2222:1x y C a b +=()0a b >>相交于A 、B 两点,O 为原点,M 为AB的中点,若直线OM 与直线l 的斜率之积为13−,则椭圆C 的离心率为______.【解析】由中点弦结论,21133OM AB k k e e ⋅=−=−⇒=.7.(★★★)已知双曲线22:13x C y −=,过点()3,1M 的直线l 与双曲线C 交于A 、B 两点,若M 恰好为AB 的中点,则直线l 的方程为______.【解析】设直线l 的斜率为k ,由中点弦结论,2213OM b k k a ⋅==,又点M 的坐标为()3,1,所以13OM k =,故1k =,显然直线l 过点M ,所以直线l 的方程为13y x −=−,化简得:2y x =− 【答案】2y x =−8.(★★★★)已知椭圆2222:1x y C a b+=()0a b >>的左、右顶点分别为A 、B ,P 是椭圆C 上的动点,直线PA 、PB 的斜率分别为1k 、2k ,若12k k +的最小值为43,则椭圆C 的离心率为______.【解析】由椭圆第三定义,21210k k e =−<,所以12k k +≥==当且仅当12k k =时取等号,结合120k k <知此时12k k =−,P 为椭圆短轴端点,所以12k k +的最小值为43=,解得:3e =.【答案】39.(★★★★)已知椭圆2222:1x y C a b+=()0a b >>的左右顶点分别为A 和B ,直线l 过点B且与x 轴垂直,P 为椭圆C 上不与A 、B 重合的动点,直线PA 与直线l 交于点M ,且OM PB ⊥,则椭圆C 的离心率为______.【解析】如图,不妨设P 在x 轴上方,设直线PA 、PB 的斜率分别为1k 、2k , 由椭圆第三定义,2121k k e =−, 由图可知12tan 2tan 212OM MB MB MBk MOB MAB k OBAB AB =∠====∠=, 因为OM PB ⊥,所以21OM k k ⋅=−,从而1221k k =−,即()2211e −=−,解得:2e =.10.(★★★)已知椭圆2222:1x y E a b+=()0a b >>的右焦点为()3,0F ,过点F 的直线交椭圆E 于A 、B 两点,若AB 中点M 的坐标为12,2⎛⎫⎪⎝⎭,则椭圆E 的方程为______.【解析】易求得12OMk =,12AB MF k k ==−,由中点弦结论,22OM AB b k k a ⋅=−,所以2214b a −=−,故224a b =,又椭圆E 的右焦点为()3,0F ,所以229a b −=,从而212a =,23b =,故椭圆E 的方程为221123x y +=.【答案】221123x y += 11.(★★★★)如下图所示,1A 、2A 为椭圆22195x y +=的左右顶点,O 为坐标原点,S 、Q 、T 为椭圆上不同于1A 、2A 的三点,且1QA 、2QA 、OS 、OT 围成一个平行四边形OPQR ,则22OS OT +=( )A.5B.3C.9D.14【解析】解法1:125599QA QA OT OS k k k k ⋅=−⇒⋅=−,设直线OT 的斜率为k ,则OS 的斜率为59k −,联立225945y kx x y =⎧⎨+=⎩可求得224559x k =+,2224559k y k =+,所以()22245159k OT k +=+, 将k 替换成59k −整理可得:222812559k OS k +=+,从而()2222224518125145959k k OS OT k k +++=+=++.解法2(极限位置分析法):让点Q 无限接近1A ,此时S 无限接近1A ,T 无限接近椭圆的上顶点,所以22OS OT +无限接近9514+=,故选D. 【答案】D12.(★★★★)如下图所示,直线l 交双曲线2222:1x y C a b−=()0,0a b >>的右支于M 、N 两点,交x 轴于点P ,M 在第一象限,N 在第四象限,O 为原点,直线MO 交双曲线C 的左支于点Q ,连接QN ,若60MPO ∠=︒,30MNQ ∠=︒,则双曲线C 的离心率为______.【解析】如图,过点Q 作x 轴的平行线交MN 于点T ,由题意,又60MPO ∠=︒,所以60MTQ ∠=︒,又30MNQ ∠=︒,所以30TQN ∠=︒, 从而直线MN 和直线NQ的斜率分别为3−, 显然M 、Q 关于原点对称,由双曲线第三定义的推广,21MN NQ k k e ⋅=−,所以2113e ⎛−=−= ⎝⎭,故双曲线C的离心率e =13.(★★★★)如下图所示,1A 、2A 分别是椭圆22162x y +=的上、下顶点,点P 是椭圆上不与1A 、2A 重合的动点,点Q 满足11QA PA ⊥,22QA PA ⊥,则12PA A 与12QA A 的面积之比1212PA A QA A S S=_______.【解析】解法1:设直线1PA 的斜率为()0k k ≠,由椭圆第三定义的推广结论,1213PA PA k k ⋅=−,所以213PA k k =−,因为11QA PA ⊥,22QA PA ⊥,所以11QA k k=−,23QA k k =,显然(1A,(20,A ,所以直线1AQ的方程为1y x k=−+,直线2A Q的方程为3y kx =, 联立直线1AQ 和2A Q的方程可解得:231x k =+,所以点Q的横坐标231Qx k =+, 直线1PA的方程为y kx =22162x y +=消去y 整理得:()22310k x ++=,解得:0x =或,所以点P的横坐标px =,由图可知12123PA A P QA A QSx Sx ===.解法2(特值法):不妨取P 为椭圆右顶点,此时P、Q 的位置如图所示,易求得1OA =OP =11tan OP OA P OA∠=,从而160OA P ∠=︒,结合11QA PA ⊥可得130OAQ ∠=︒,故11tan 3OQ OA OAQ =⋅∠=,所以12123PA A QA A S OP SOQ==【答案】314.(★★★★)已知双曲线2222:1x y C a b −=()0,0a b >>的左、右顶点分别为A 、B ,圆()222:2D x y a a +−=与双曲线C 在第一象限的交点为P ,记直线PA 、PB 的斜率分别为1k 、2k ,若212k k −=,则双曲线C 的离心率为______.【解析】如图,记PAB α∠=,PBA β∠=,则1tan k α=,()2tan tan k πββ=−=−, 由题意,(),0A a −,(),0B a ,()0,D a ,所以ABD 是以D 为直角顶点的等腰直角三角形, 容易验证A 、B 两点都在圆D 上,所以124APB ADB π∠=∠=,从而tan 1APB ∠=,另一方面,()()tan tan tan tan tan 1tan tan APB αβπαβαβαβ+∠=−−=−+=−−,所以tan tan 11tan tan αβαβ+−=−①由双曲线第三定义,2121k k e =−,所以()2tan tan 1e αβ⋅−=−,从而2tan tan 1e αβ=−,又212k k −=,所以tan tan 2βα−−=,故tan tan 2βα+=−,代入式①可得()22111e −−=−−,解得:e =15.(★★★★)已知斜率为13−的直线l 与椭圆22197x y +=相交于不同的两点A 、B ,M 为y 轴上一点,且MA MB =,则点M 的纵坐标的取值范围是______.【解析】如图,设AB 中点为()00,N x y ,由中点弦结论,001739y x −⋅=−,所以0073y x =①,因为N 为AB 中点,所以点N 在椭圆内部,从而2200197x y +<将式①代入可解得:0x < 因为M 在y 轴上,且MA MB =,所以点M 是AB 的中垂线与y 轴的交点, 易求得AB 的中垂线的方程为()003y y x x −=− 即0033y x y x =+−,从而点M 的纵坐标003M y y x =−,将式①代入可得023M y x =−,因为044x −<<,所以22M y −<<.【答案】22⎛⎫⎪ ⎪⎝⎭。
【例1】若椭圆()0122 n m n y m x =+与双曲线221x y a b-=)0( b a 有相同的焦点F 1,F 2,P 是两条曲线的一个交点,则|PF 1|·|PF 2|的值是 ( )A. a m -B. ()a m -21C. 22a m -D. a m -【解析】椭圆的长半轴为()121PF PF ∴+=()122PF PF ∴-=±()()()2212121244PF PF m a PF PF m a -⋅=-⇒⋅=-:,故选A.【评注】严格区分椭圆与双曲线的第一定义,是破解本题的关键.【例2】已知双曲线127922=-y x 与点M (5,3),F 为右焦点,若双曲线上有一点P ,使PM PF21+最小,则P 点的坐标为 【分析】待求式中的12是什么?是双曲线离心率的 倒数.由此可知,解本题须用双曲线的第二定义.【解析】双曲线的右焦点F (6,0),离心率2e =,右准线为32l x =:.作MN l ⊥于N ,交双曲线右支于P ,连FP ,则122PF e PN PN PN PF ==⇒=.此时PM 1375225PF PM PN MN +=+==-=为最小.在127922=-y x 中,令3y =,得212x x x =⇒=±∴0,取x =所求P 点的坐标为().(2)渐近线——双曲线与直线相约天涯对于二次曲线,渐近线为双曲线所独有. 双曲线的许多特性围绕着渐近线而展开.双曲线的左、右两支都无限接近其渐近线而又不能与其相交,这一特有的几何性质不仅很好地界定了双曲线的范围.由于处理直线问题比处理曲线问题容易得多,所以这一性质被广泛应用于有关解题之中.【例3】过点(1,3)且渐近线为x y 21±=的双曲线方程是【解析】设所求双曲线为()2214x y k -=点(1,3)代入:135944k=-=-.代入(1): 22223541443535x y x y -=-⇒-=即为所求. 【评注】在双曲线22221x y a b-=中,令222200x y x y a b a b -=⇒±=即为其渐近线.根据这一点,可以简洁地设待求双曲线为2222x y k a b -=,而无须考虑其实、虚轴的位置.XYO F(6,0)M(5,3)P N P ′N ′X=32(3)共轭双曲线—— 虚、实易位的孪生弟兄将双曲线22221x y a b -=的实、虚轴互易,所得双曲线方程为:22221x y b a-=.这两个双曲线就是互相共轭的双曲线.它们有相同的焦距而焦点的位置不同;它们又有共同的渐近线而为渐近线所界定的范围不一样;它们的许多奇妙性质在解题中都有广泛的应用.【例4】两共轭双曲线的离心率分别为21,e e ,证明:221211e e +=1.【证明】双曲线22221x y a b -=的离心率22221122c c a b e e a a a +=⇒==;双曲线22221x y b a-=的离心率22222222c c a b e e b b b +=⇒==.∴2222222212111a b e e a b a b+=+=++.(4)等轴双曲线——和谐对称 与圆同美实、虚轴相等的双曲线称为等轴双曲线,等轴双曲线的对称性可以与圆为伴.【例5】设CD 是等轴双曲线的平行于实轴的任一弦,求证它的两端点与实轴任一顶点的连线成直角. 【证明】如图设等轴双曲线方程为()2221x y a -=,直线CD :y=m.代入(1):22x x m=±+.故有:()()2222,,,C x m m Dx m m-++.取双曲线右顶点(),0Ba .那么:()()2222,,,BC x m a m BD x m a m=-+-=+-()22220,BC BD a a m m BC BD ⎡⎤⋅=-++=∴⊥⎣⎦.即∠CBD=90°. 同理可证:∠CAD=90°.● 通法 特法 妙法(1)方程法——为解析几何正名解析法的指导思想是函数方程思想,其主要手段是列、解方程、方程组或不等式.【例6】如图,1F 和2F 分别是双曲线)0,0(12222>>=-b a by a x 的两个焦点,A 和B 是以O 为圆心,以1F O 为半径的圆与该双曲线左支的两个交点,且△AB F 2是等边三角形,则双 曲线的离心率为( )(A )3 (B )5 (C )25 (D )31+XOYCDA B【解析1】设AB 交x 轴于M ,并设双曲线半焦距为c ,∵△AB F 2是等边三角形,∴,.22c OM MA c ==点2c A ⎛⎫- ⎪ ⎪⎝⎭代入双曲线方程:()()2222222222222233444c b a c a b c c a a c a c a ⋅-⋅=⇒--=-.化简得:422442284084041c a c a e e e e -+=⇒-+=⇒=+=.(∵e >1,∴24e=-及1e =舍去)故选D.【解析2】连AF 1,则△AF 1F 2为直角三角形,且斜边F 1F 2之长为2c.令1122,.AF r AF r ==由直角三角形性质知:211221221222r r ar c r a c r c r r -=⎧=⎧⎪⇒⎨⎨=+⋅=⎩⎪⎩. ∵()222222222124,24220220r r c a c c c a ac c e e +=∴++=⇒+-=⇒--=.∵e ﹥1,∴取1e =.选D.【评注】即使是解析法解题,也须不失时机地引入几何手段.(2)转换法——为解题化归立意【例7】直线l 过双曲线12222=-by a x 的右焦点,斜率k =2.若l 与双曲线的两个交点分别在左右两支上,则双曲线的离心率e 的范围是 ( )A .e >2 B.1<e <3 C.1<e <5 D.e >5【分析】就题论题的去解这道题,确实难以下手,那就 考虑转换吧.其一,直线和双曲线的两支都有交点不好掌握, 但是和两条渐近线都有交点却很好掌握.其二,因为已知直线 的斜率为2,所以双曲线的两条渐近线中,倾斜角为钝角的 渐近线肯定与之相交,只须考虑倾斜角为锐角的渐近线也与 之相交.故有如下妙解.【解析】如图设直线l 的倾斜角为α,双曲线渐近线m 的倾斜角为β.显然。
当β>α时直线l 与双曲线的两个交点分别在左右两支上.由2222tan tan 245b c a e a aβαβα->⇒>⇒>⇒>⇒>. ∵双曲线中1e >,故取e >5.选D.(3)几何法——使数形结合带上灵性【例8】设P 为双曲线22112y x -=上的一点,12F F ,是该双曲线的两个焦点,若12||:||3:2PF PF =,则12PF F △的面积为XYO Fl( )A.B .12C. D .24【解析】双曲线的实、虚半轴和半焦距分别是:1,a b c ===.设;12123,2.22, 2.PF r PF r PF PF a r ==-==∴= 于是2221212126, 4.52PF PF PF PF F F ==+==,故知△PF 1F 2是直角三角形,∠F 1P F 2=90°.∴121211641222PF FS PF PF ∆=⋅=⨯⨯=.选B. 【评注】解题中发现△PF 1F 2是直角三角形,是事前 不曾想到的吧?可是,这一美妙的结果不是每个考生都能 临场发现的.将最美的结果隐藏在解题过程之中以鉴别考生的思维 能力,这正是命题人的高明之处.(4)设而不求——与借舟弃舟同理减少解析几何计算量的有效方法之一便是设而不求.请看下例: 【例9】双曲线122=-y x 的一弦中点为(2,1),则此弦所在的直线方程为 ( )A.12-=x y B. 22-=x y C. 32-=x y D. 32+=x y【解析】设弦的两端分别为()()1,12,2,Ax y B x y .则有:()()222222111212121222121222101x y y y x x x x y y x x y y x y ⎧-=-+⇒---=⇒=⎨-+-=⎩.∵弦中点为(2,1),∴121242x x y y +=⎧⎨+=⎩.故直线的斜率121212122y y x x k x x y y -+===-+. 则所求直线方程为:()12223y x y x -=-⇒=-,故选C.“设而不求”具体含义是:在解题中我们希望得到某种结果而必须经过某个步骤,只要有可能,可以用虚设代替而不必真地去求它. 但是,“设而不求”的手段应当慎用.不问条件是否成熟就滥用,也会出漏子.请看:【例10】在双曲线1222=-y x 上,是否存在被点M (1,1)平分的弦?如果存在,求弦所在的直线方程;如不存在,请说明理由. 如果不问情由地利用“设而不求”的手段,会有如下解法:【错解】假定存在符合条件的弦AB ,其两端分别为:A (x 1,y 1),B (x 2,y 2).那么:()()()()()22111212121222221112011212x y x x x x y y y y x y ⎧-=⎪⎪⇒-+--+=⎨⎪-=⎪⎩.∵M (1,1)为弦AB 的中点,∴()()()1212121212122022AB x x y y x x y y k y y x x +=⎧----=∴==⎨+=-⎩代入1:2,故存在符合条件的直线AB ,其方程为:()12121y x y x -=-=-,即.这个结论对不对呢?我们只须注意如下两点就够了:其一:将点M (1,1)代入方程1222=-y x ,发现左式=1-1122=<1,故点M (1,1)在双曲线的外部;其二:所求直线AB 的斜率2ABk =,而双曲线的渐近线为y =.2,说明所求直线不可能与双曲线相交,当然所得结论也是荒唐的.问题出在解题过程中忽视了直线与双曲线有公共点的条件. 【正解】在上述解法的基础上应当加以验证.由()()222221221224302221y x x x x x y x ⎧-=⎪⇒--=⇒-+=⎨⎪=-⎩这里16240∆=-,故方程(2)无实根,也就是所求直线不合条件.此外,上述解法还疏忽了一点:只有当12x x ≠时才可能求出k=2.若12120x x y ===,必有y .说明这时直线与双曲线只有一个公共点,仍不符合题设条件.结论;不存在符合题设条件的直线.(5)设参消参——换元自如 地阔天宽一道难度较大的解析几何综合题,往往牵涉到多个变量.要从中理出头绪,不能不恰当地处理那些非主要的变量,这就要用到参数法,先设参,再消参.【例11】如图,点F 为双曲线C 的左焦点,左准线l 交x1||||==FQ PQ ,且线段PF 的中点M 在双曲线C 的左支上.(Ⅰ)求双曲线C 的标准方程;(Ⅱ)若过点F 的直线m 与双曲线C 的左右 两支分别交于A 、B 两点,设FA FB λ=,当),6[+∞∈λ时,求直线m 的斜率k 的取值范围.【分析】第(Ⅰ)问中,线段PF 的中点M 的坐标是主要变量,其它都是辅助变量.注意到点M 是直角三角形斜边的中点,所以利用中点公式是设参消参的主攻方向第(Ⅱ)中,直线m 的斜率k 是主要变量,其它包括λ都是辅助变量. 斜率k 的几何意义是有关直线倾斜角θ的正切,所以设置直线m 的参数方程,而后将参数λ用θ的三角式表示,是一个不错的选择.【解析】(Ⅰ)设所求双曲线为:22221x y a b-=.其左焦点为F (-c 。