单个点电荷产生的电场

什么是电场和磁场它们之间的关系是什么电场和磁场是物理学中两个重要的概念，它们分别描述了电荷和磁荷所产生的力场。

本文将会详细介绍电场和磁场的基本概念，以及它们之间的关系。

一、电场的概念与性质电场是由电荷所产生的力场，描述了电荷对其他电荷或物质所施加的力。

电荷在空间中产生电场，电场的强度和方向受到电荷的大小和符号的影响。

假设有一个点电荷q位于空间中的某一位置P，那么在离该点电荷一定距离r处，点电荷所产生的电场强度E的大小与距离r的平方成反比，即E∝1/r^2。

根据库仑定律，电场强度的大小还与电荷的大小q成正比，即E∝q/r^2。

因此，电场强度的大小与点电荷的大小和距离的平方成反比。

二、磁场的概念与性质磁场是由磁荷所产生的力场，描述了磁荷对其他磁荷或物质所施加的力。

磁荷是一种基本的物理概念，但在目前的物理学中并没有发现单个的磁荷存在，我们所讨论的磁场主要是由电流所产生的。

磁场的强度和方向由电流的大小和方向决定。

根据安培定律，电流元产生的磁场强度dH对距离r的矢量短元dL的影响与电流元的大小和方向有关，可以表示为dH=kI(dL×r)/r^3，其中I为电流的大小，dL×r为矢量叉乘，k为比例常数。

根据电流元对磁场的贡献是矢量叠加的原理，可以得到磁场强度H的大小和方向。

三、电场和磁场的关系电场和磁场在物理学中经常会相互作用，它们之间有着密切的关系。

根据麦克斯韦方程组，电场和磁场之间的相互作用可以用法拉第电磁感应定律和安培定律来描述。

法拉第电磁感应定律指出，磁场的变化可以产生感应电压，即电磁感应现象。

而安培定律则表明，电流元所产生的磁场可以影响到电荷的运动，进而改变电荷所受的力。

另外，从电场和磁场的数学表示可以看出它们之间的相互关系。

电场可以用电势表示，而磁场则可以用矢量磁势表示。

根据麦克斯韦方程组的推导可以发现，电场的旋度为零，而磁场的散度为零，这意味着电场是保守场，而磁场是无源场。

因此，在稳恒情况下，电场可以通过势函数来描述，而磁场则需要通过磁通量来描述。

等量异种点电荷电场线以及电势分布
不同种类点电荷的电场与电势分布
一、单独的正电荷
1.电场线：当一个单独的正电荷放置在多普勒空间中时，由其产生的电场线从电荷所在的空间点出发，沿着无穷远处的那个方向延伸出去，
并且这些电场线的密度随着离正电荷的距离而不断减少。

2.电势分布：当正电荷放置在多普勒空间中时，它的电势能随着离正电荷的距离而不断减少。

由此可以确定，电势分布表明，在多普勒空间中，从正电荷出发的所有方向上，距离电荷一定距离处的电势一定比
距离电荷更远处的电势小。

二、单独的负电荷
1.电场线：当一个单独的负电荷放置在多普勒空间中时，由其产生的电场线也从电荷所在的空间点出发，沿着无穷远处的那个方向延伸出去，但电场线的密度却在随着离负电荷的距离而增加。

2.电势分布：当负电荷放置在多普勒空间中时，由于它的电势会随着距离电荷的增加而不断增大，因此电势分布表明，在多普勒空间中，从
负电荷出发的所有方向上，距离负电荷一定距离处的电势一定比距离负电荷更远处的电势大。

三、负正混合电荷
1.电场线：当负正混合电荷放置在多普勒空间中时，由正负电荷及其相互之间的相互作用产生的电场线，从一个正电荷沿着一定的方向延伸出去，指向一个负电荷，并且再经过负电荷时直接折返，沿着原来的方向延伸；从一个负电荷出发则指向一个正电荷，并且与前述情况相对应。

2.电势分布：当负正混合电荷放置在多普勒空间中时，由于由正负电荷及其相互之间的相互作用所产生的电势会在正负电荷之间依次发生变化，其越近正电荷处的位置，则电势越大；越接近负电荷处的位置，则电势越小。

以此，可以准确地判断电势分布的变化规律，即正负电荷的电势分布发生的变化越来越接近线性的变化规律。

电场的分布规律在物理学中，电场是一个十分重要的概念。

它描述了电荷之间相互作用的力场，同时也对电荷的运动和电磁现象产生影响。

电场的分布规律是研究电荷分布情况及其相应电场分布的规律性规定。

本文将从不同电荷分布情况出发，探讨电场的分布规律。

一、点电荷的电场分布规律首先，让我们考虑最简单的情况，即一个点电荷的电场分布。

对于一个单个的正电荷，其电场按照与该点电荷距离的平方成反比的规律分布。

根据库仑定律，点电荷产生的电场强度E与距离r的关系可由以下公式表示：E = k * (Q / r^2)其中，E为电场强度，Q为电荷大小，r为距离，k为库仑常数。

从上述公式可以看出，点电荷的电场强度随距离的增加而减小，呈现出与距离r的平方成反比的关系。

二、均匀带电直线的电场分布规律接下来，我们考虑均匀带电直线的电场分布。

对于沿一条直线均匀分布的电荷，其电场分布具有轴对称性。

通过计算可以得出，均匀带电直线的电场强度E与距离r之间的关系为：E = (k * λ) / r其中，E为电场强度，λ为单位长度上的电荷密度，r为距离，k为库仑常数。

需要注意的是，在这种情况下，电场强度E与距离r呈反比的关系，但是与距离的平方没有直接关系。

三、均匀带电平面的电场分布规律除了直线分布的电荷，我们还可以考虑平面分布的电荷情况。

在均匀带电平面的情况下，平面上各点的电场方向相同且大小相等，其大小只与平面上的位置有关。

根据计算可以得到，均匀带电平面的电场强度E与距离关系没有直接的简单公式表示。

但是，我们可以得出以下结论：1. 与平面垂直方向的电场强度是均匀分布的，与距离无关。

2. 与平面平行方向的电场强度与距离成反比，但与距离的平方无直接关系。

四、其他电荷分布情况下的电场分布规律在实际情况中，我们会遇到各种复杂的电荷分布情况。

对于这些情况，我们可以通过应用高斯定律和数值计算等方法来得到电场分布的规律。

高斯定律是研究电场分布的重要方法之一，它表明电场通量与所选闭合曲面内电荷的总量成正比，与所选闭合曲面的形状无关。

6.4.5电势的计算方法一般说来，计算电势的方法有两种。

第一种方法是由电势的定义式通过场强的线积分来计算；另一种方法是下面马上就要介绍的电势叠加原理。

对不同的带电体系，本质上讲上述两种方法都能够计算出电势，但是选择不同的方法计算的难易程度是大不相同的。

通过后面内容的学习，大家要注意对不同的带电体系选择不同的计算方法。

下面我们介绍电势迭加原理。

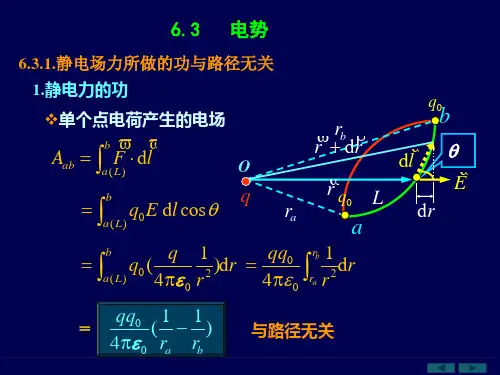
1、点电荷电场的电势如右图所示，一个点电荷q处于O点处。

在q所产生的电场中，距离O点为r处P点的电势，可以根据电势的定义式计算得到。

选无穷远处作为电势零点，积分路径沿O P方向由P点延伸到无穷远。

由于积分方向选取得与场强点电荷的电势的方向相同，P点电势可以很容易地计算出来此式给出点电荷电场中任意一点的电势大小，称作点电荷电势公式。

公式中视q的正负，电势V可正可负。

在正点电荷的电场中，各点电势均为正值，离电荷越远的点，电势越低，与r成反比。

在负点电荷的电场中，各点的电势均为负，离电荷越远的点，电势越高，无穷远处电势为零。

容易看出，在以点电荷为心的任意球面上电势都是相等的，这些球面都是等势面。

2、电势的叠加原理在前面的知识点中，大家学习了场强叠加原理。

该原理告诉我们，任意一个静电场都可以看成是多个或无限多个点电荷电场的叠加，即有其中E表示总电场，E1，E2，…为单个点电荷产生的电场。

根据电势的定义式，并应用场强叠加原理，电场中a点的电势可表示为上式最后面一个等号右侧被求和的每一个积分分别为各个点电荷单独存时在a点的电势。

即有式中V a i是第i个点电荷单独存在时在a点产生的电势。

显然，如果我们将带电体系分成若干部分（不一定是点电荷），上述结论仍然是正确的。

即，任意一个电荷体系的电场中任意一点的电势，等于带电体系各部分单独存在时在该点产生电势的代数和。

这个结论叫做电势叠加原理。

若一个电荷体系是由点电荷组成的，则每个点电荷的电势可以按上式进行计算，而总的电势可由电势叠加原理得到，即式中r i是从点电荷q i到a点的距离。

点电荷的电场线和等势线解析根据库仑定律，一试验电荷q 0与点电荷Q 相距为r 时，受到的静电力为F ＝kQq 0r 2 其中k 是静电力常量，k = 9×109N·m 2/C 2。

根据电场强度的定义，点电荷Q 在r 处产生的电场强度大小为E ＝F q 0＝kQ r 2 可见：点电荷的带电量Q 越大，在周围空间产生的场强越大；场强与距离的平方成反比。

如果Q 是正电荷，场强方向沿着径向向外；如果Q 是负电荷，场强方向沿着径向向内。

以无穷远处为电势零点，取一条从r 到无穷远处的电场线为积分路径，点电荷在r 处的电势为U ＝ E ⋅ⅆs ∞0＝ E ⅆr ∞0＝kQ r 2ⅆr ∞0＝kQ r可见：点电荷的电势与距离成反比。

图示点电荷的电场线是以点电荷为端点的射线。

对于正的点电荷，射线从点电荷射向四周；对于负的点电荷，射线从四周射向点电荷。

在点电荷的平面上，点电荷的等势线是以点电荷为中心的圆，相邻两个等势线之间的电势差应该相等。

不论是正电荷还是负电荷，场点离电荷距离越近，电场线越密，等势线也越密，场强越大。

注：上图的格式是emf，编辑有所不便，在此图基础上进行转换，如下图：算法为了计算数值，取某一点的距离r0作为参考距离，也就是距离的单位，则电场强度大小可表示为E＝kQr02(r/r0)2＝E0r*2其中，r*=r/r0，是无量纲的距离或约化距离；E0=kQ/r02是r0处的场强大小。

取E0为场强单位，E/E0就是无量纲的场强或约化场强。

显然：点电荷的无量纲场强E/E0与无量纲的距离的平方成反比。

电势可表示为U＝kQr0(r/r0)＝U0r*其中，U0=kQ/r0，是r0处的电势。

取U0为电势单位，U/U0是无量纲的电势或约化电势，与无量纲的距离成反比。

等势线通常用等值线指令contour绘制，由于点电荷的等势线是同心圆，也可用矩阵画线法绘制。

由于点电荷的电场线是射线，所以用箭杆指令quiver绘制比较简单。

电势能ep的公式电势能公式：ep=wao=q·φa=qua(ep表示电势能，φa表示a点的电势）：当φa\ue0时，q\ue0,则ep\ue0，q\uc0，则ep\uc0；当φa\uc0时，q\ue0，则ep\uc0，q\uc0，则ep\ue0。

wab=epa-epb。

1、电势能各类公式（1）电势与电势差：uab＝φa-φb，uab＝wab/q＝-δeab/q（2）势能：ea＝qφa｛ea:带电体在a点的电势能(j)，q:电量(c)，φa:a点的电势(v)｝电势能的变化δeab＝eb-ea｛带电体在电场中从a位置到b位置时电势能的差值｝电场力做功与电势能变化δeab＝-wab＝-quab(电势能的增量等于电场力做功的负值)2、排序电势的方法一般说来，计算电势的方法有两种。

第一种方法是由电势的定义式通过场强的线积分来计算；另一种方法是下面马上就要介绍的电势叠加原理。

对不同的带电体系，本质上讲上述两种方法都能够计算出电势，但是选择不同的方法计算的难易程度是大不相同的。

（1）点电荷电场的电势：点电荷电场中任一一点的电势大小，称为点电荷电势公式。

公式中视q的差值，电势v可正可负。

在也已点电荷的电场中，各点电势均为正值，距电荷越远的点，电势越高，与r成反比。

在负点电荷的电场中，各点的电势均为负，距电荷越远的点，电势越高，无穷远处电势为零。

难窥见，在以点电荷为心的任意球面上电势都就是成正比的，这些球面都就是等势面。

（2）电势的叠加原理：e表示总电场，e1，e2，…为单个点电荷产生的电场。

根据电势的定义式，并应用场强叠加原理，电场中a点的电势可表示为上式最后面一个等号右侧被求和的每一个积分分别为各个点电荷单独存时在a点的电势。

即有式中vai是第i个点电荷单独存在时在a点产生的电势。

3、电势能变化量（1）电场力做的功与电势能变化量起点和终点状态恒定的点电荷，电场力作功与电势能变化量的关系：电势能的变化量也可以则表示为△ep=epb-epa，因此存有wab=-△ep 。

点电荷产生的电场强度
电场是一种物理场，它可以通过电荷之间的相互作用来描述。

在电场中，点电荷产生的电场强度是一个重要的物理量，它描述了电场在空间中的强度和方向。

当一个点电荷Q存在时，它会在周围产生一个电场。

这个电场的强度可以通过电场强度公式来计算。

根据库仑定律，点电荷Q在距离r处产生的电场强度E可以表示为：
E = k Q / r^2。

其中，k是库仑常数，约为8.99 10^9 N·m^2/C^2，r是点电荷到观察点的距离。

从这个公式可以看出，点电荷产生的电场强度与电荷量Q成正比，与距离r的平方成反比。

这意味着电场强度随着距离的增加而减小，同时与电荷量的增加而增加。

电场强度的方向与电荷的正负有关，如果点电荷为正电荷，则电场强度指向远离电荷的方向；如果点电荷为负电荷，则电场强度
指向电荷的方向。

点电荷产生的电场强度在物理学中有着广泛的应用，它可以帮助我们理解电荷之间的相互作用，以及在电场中的电荷受到的力和运动。

同时，电场强度也是电场能量密度和电场势能的重要参数，对于电场的研究和应用具有重要意义。

总之，点电荷产生的电场强度是描述电场中电荷相互作用的重要物理量，通过电场强度公式可以计算出电场的强度和方向，它在物理学和工程技术中都有着重要的应用价值。

点电荷电场强度叠加公式
一、点电荷电场强度公式。

1. 单个点电荷的电场强度。

- 真空中静止点电荷Q在距离它r处产生的电场强度E = k(Q)/(r^2)，其中
k=(1)/(4πvarepsilon_0)，varepsilon_0是真空介电常数，k = 9.0×10^9N· m^2/C^2。

二、点电荷电场强度叠加原理。

1. 原理阐述。

- 电场强度是矢量，当空间存在多个点电荷时，某点的电场强度等于各个点电荷单独在该点产生的电场强度的矢量和。

2. 叠加公式。

- 设有n个点电荷Q_1,Q_2,·s,Q_n，在空间某点P的电场强度E为E =
E_1+E_2+·s+E_n，其中E_i = k(Q_i)/(r_i)^2r_i（r_i是从点电荷Q_i指向P点的单位矢量）。

- 具体计算时，需要先根据点电荷电场强度公式分别计算出每个点电荷在该点的电场强度大小和方向，然后再根据矢量加法的平行四边形定则（或三角形定则）进行矢量叠加。

例如在直角坐标系中，可以将各个电场强度分解为x、y、z方向的分量，分别叠加后再合成得到总电场强度。

大学物理静电场知识点总结1.电荷的基本特点：（1）分类：正电荷（同质子所带电荷），负电荷（同电子所带电荷）（2）量子化特征（3）是相对论性不变量（4）微观粒子所带电荷老是存在一种对称性2．电荷守恒定律：一个与外界没有电荷互换的孤立系统，不论发生什么变化，整个系统的电荷总量必然保持不变。

3．点电荷：点电荷是一个宏观范围的理想模型，在可忽视带电体自身的线度时才建立。

4．库仑定律：表示了两个电荷之间的静电互相作用，是电磁学的基本定律之一，是表示真空中两个静止的点电荷之间互相作用的规律r1 q1q2 rF1240 r123r 125．电场强度：是描绘电场状况的最基本的物理量之一，反应了电rr F场的基Eq0 6．电场强度的计算：（1）单个点电荷产生的电场强度，可直接利用库仑定律和电场强度的定义来求得（2）带电体产生的电场强度，能够依据电场的叠加原理来求解r1nq i r r1dq rE r i E r40 i 1 r i3r 340（3）拥有必定对称性的带电体所产生的电场强度，能够依据高斯定理来求解（4）依据电荷的散布求电势，而后经过电势与电场强度的关系求得电场强度7．电场线：是一些虚假线，引入其目的是为了直观形象地表示电场强度的散布（1）电场线是这样的线： a．曲线上每点的切线方向与该点的电场强度方向一致b．曲线散布的疏密对应着电场强度的强弱，即越密越强，越疏越弱。

（2）电场线的性质： a．起于正电荷（或无量远），止于负电荷（或无量远）。

b．不闭合，也不在没电荷的地方中止。

c．两条电场线在没有电荷的地方不会订交8．电通量：e s r r E dS（1）电通量是一个抽象的观点，假如把它与电场线联系起来，能够把曲面 S 的电通量理解为穿过曲面的电场线的条数。

（2）电通量是标量，有正负之分。

9．高斯定理：òs r r1E dS q i0（ S里）r（1）定理中的E是由空间全部的电荷（包含高斯面内和面外的电荷）共同产生。

§1-2 电场 电场强度一、电场库仑定律确定了点电荷之间的相互作用力的规律，但这种力究竟是怎样进行的？近代物理学认为：电荷周围存在着一种特殊的物质，借以传递电荷之间的相互作用，这种特殊的物质就是电场。

两电荷之间的静电力实际上是每一个电荷的电场作用在另一个电荷上的作用力——电场力。

这种作用力可图示为二、电场强度1、 试探电荷0q （约定为正）为了研究电场中各点的性质，我们引入这样一种点电荷，它需要满足以下两个条件⎧⎨⎩线度小到可以看作一个几何点电量小到引入它时不影响原电场的分布，这种点电荷称为试探电荷，它本身带电可正、可负，但一般约定为正。

2、 电场强度将试探电荷放到电场中不同点时，他受到的力的大小和方向一般是不同的。

为了表征电场的这种力的性质，我们引入电场强度这个物理量。

如图，把一个电荷Q 放在真空中，在其周围空间就产生了电场，若0q 在此场中某点受力为F ，则0Fq就称为该点的电场强度，用E 表示，即FE q = （场强定义式）物理意义：电场中某点的电场强度，在量值和方向上等于一个单位正电荷在该点所受的力。

说明：⑴E 不是0q 产生的，E是否存在与0q 无关；⑵E 是矢量 电场中某点电场强度的大小：0FE q = ，等于单位电荷在该点所受电场力的大小；方向：与正电荷在该点受力方向相同。

⑶E 是矢量点函数，在直角坐标系中可记作(),,E x y z；如果空间各点的E 相同，则称该空间存在一个匀强电场。

⑷单位（SI ）：()1N C -⋅牛顿库仑（定义式可给出），或者，()1V m -⋅伏特米。

（UE d=可给出） 三、电场强度的计算1、 单个点电荷产生的电场把一个点电荷q 放在真空中，在其周围就产生了电场，利用场强的定义式和库仑定律，可给出其中空间任意一点P 的场强。

引入试探电荷。

由库仑定律，q 对0q 的作用力 02014qq F r rπε= ，其中r 是场源电荷q 指向场点P 的单位矢量；•Q 0q F则再由场强的定义式，可得到单个点电荷在空间某点P 产生的场强为20014F q E r q r πε==。

大学物理静电场知识点总结1.电荷的基本特征：（1）分类：正电荷（同质子所带电荷），负电荷（同电子所带电荷）（2）量子化特性（3）是相对论性不变量（4）微观粒子所带电荷总是存在一种对称性2．电荷守恒定律：一个与外界没有电荷交换的孤立系统，无论发生什么变化，整个系统的电荷总量必定保持不变。

3．点电荷：点电荷是一个宏观范围的理想模型，在可忽略带电体自身的线度时才成立。

4．库仑定律：表示了两个电荷之间的静电相互作用，是电磁学的基本定律之一，是表示真空中两个静止的点电荷之间相互作用的规律r1 q1q2 rF1240 r123r 125．电场强度：是描述电场状况的最基本的物理量之一，反映了电rr F场的基 Eq0 6．电场强度的计算：（1）单个点电荷产生的电场强度，可直接利用库仑定律和电场强度的定义来求得（2）带电体产生的电场强度，可以根据电场的叠加原理来求解r 1nq i r r 1 dq rE r i E r4 0 i 1 r i3 r 34 0（3）具有一定对称性的带电体所产生的电场强度，可以根据高斯定理来求解（4）根据电荷的分布求电势，然后通过电势与电场强度的关系求得电场强度7．电场线：是一些虚构线，引入其目的是为了直观形象地表示电场强度的分布（1）电场线是这样的线： a．曲线上每点的切线方向与该点的电场强度方向一致b．曲线分布的疏密对应着电场强度的强弱，即越密越强，越疏越弱。

（2）电场线的性质： a．起于正电荷（或无穷远），止于负电荷（或无穷远）。

b．不闭合，也不在没电荷的地方中断。

c．两条电场线在没有电荷的地方不会相交8．电通量：e s r r E dS（1）电通量是一个抽象的概念，如果把它与电场线联系起来，可以把曲面 S 的电通量理解为穿过曲面的电场线的条数。

（2）电通量是标量，有正负之分。

9．高斯定理：òs r r 1E dS q i0（ S 里）r（1）定理中的E是由空间所有的电荷（包括高斯面内和面外的电荷）共同产生。