点电荷的电场

电场中的点电荷与电势能电场是物理学中重要的概念，是描述电荷间相互作用的力场。

在电场中，点电荷的存在会引发一系列的现象，其中之一就是电势能的变化。

本文将以电场中的点电荷与电势能为主题，探讨其中的关系和相关概念。

一、电场介绍电场是由电荷产生的力场，其中正电荷会引起电场线从该点指向外部空间，负电荷则相反。

电场的方向是指电力所能使正电荷运动的方向，而电场的强弱则由电场强度表示。

电场强度的大小与距离的平方成反比，与电荷量成正比。

二、点电荷点电荷是物理学中用来模拟电荷分布的理想化模型。

在电场中，点电荷的电场强度和电势能分别由库仑定律和电势能公式表示。

库仑定律指出，点电荷的电场强度与其电荷量成正比，与距离的平方成反比。

而电势能公式则描述了点电荷在电场中的能量分布情况。

三、电势能电势能是描述电荷在电场中能量状态的物理量。

在电场中，电势能可以分为势能球和势能面两种描述方式。

势能球是以点电荷为中心构成的球面，球面上每一点的势能相同。

而势能面则是以等势线所构成的面，面上每一点的势能也相同。

根据电场中电势能的定义，点电荷所具有的电势能与其位置有关，距离点电荷越近，则电势能越高。

四、电势能的计算要计算点电荷在电场中的电势能，可以利用电势能公式。

电势能公式为E=(1/4πε₀)*(q/r)，其中E表示电势能，ε₀为真空中的介电常数，q为点电荷的电荷量，r为点电荷与参考点的距离。

通过该公式，我们可以计算出点电荷在电场中的电势能分布情况。

五、电势能的应用电势能的概念和计算方法不仅在理论研究中有重要应用，也在实际生活中有着广泛的应用。

电势能是电动势和电势差的重要组成部分，对于电路分析和电子设备设计都具有重要意义。

同时，在电场中，根据电势能的分布情况，我们可以推导出电场线的形状，进而分析电荷的运动轨迹和电场的分布情况。

六、总结电场中的点电荷与电势能是电学中重要且常见的概念。

点电荷的存在会引发电场的产生，并使电势能发生变化。

通过电势能公式和电场分布情况，我们可以计算和分析点电荷在电场中的电势能分布和电场线的形状。

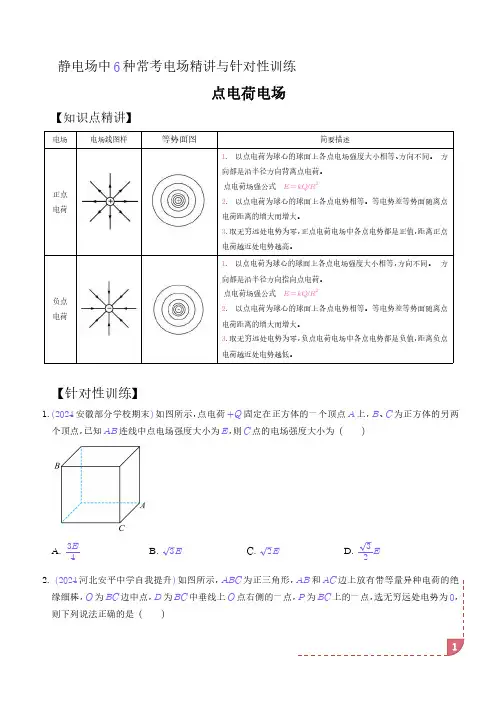
静电场中6种常考电场精讲与针对性训练点电荷电场【知识点精讲】电场电场线图样等势面图简要描述正点电荷1.以点电荷为球心的球面上各点电场强度大小相等、方向不同。

方向都是沿半径方向背离点电荷。

点电荷场强公式E =kQ /R 22.以点电荷为球心的球面上各点电势相等。

等电势差等势面随离点电荷距离的增大而增大。

3.取无穷远处电势为零，正点电荷电场中各点电势都是正值，距离正点电荷越近处电势越高。

负点电荷1.以点电荷为球心的球面上各点电场强度大小相等，方向不同。

方向都是沿半径方向指向点电荷。

点电荷场强公式E =kQ /R 22.以点电荷为球心的球面上各点电势相等。

等电势差等势面随离点电荷距离的增大而增大。

3.取无穷远处电势为零，负点电荷电场中各点电势都是负值，距离负点电荷越近处电势越低。

【针对性训练】1.(2024安徽部分学校期末)如图所示，点电荷+Q 固定在正方体的一个顶点A 上，B 、C 为正方体的另两个顶点，已知AB 连线中点电场强度大小为E ，则C 点的电场强度大小为()A.3E 4B.3EC.2ED.32E 2.(2024河北安平中学自我提升)如图所示，ABC 为正三角形，AB 和AC 边上放有带等量异种电荷的绝缘细棒，O 为BC 边中点，D 为BC 中垂线上O 点右侧的一点，P 为BC 上的一点，选无穷远处电势为0，则下列说法正确的是()A.O 点和D 点场强可能大小相等，方向相同B.D 点的电势一定低于P 点C.将一正检验电荷沿直线从O 点运动到D 点，电势能不变D.将一正检验电荷沿直线从O 点运动到P 点，电场力做负功3.(2024河南驻马店期末)地球是一个带电体，且电荷均匀分布于地球表面。

若地球所带电荷量为Q 、半径为R ，认为地球所带电荷量集中于地球中心，静电力常量为k ，则地球表面附近的电场强度大小为()A.kQR B.2kQR C.kQR 2 D.2kQ R 24.真空中某点电荷的等势面示意图如图所示,图中相邻等势面间电势差相等。

第4节点电荷的电场匀强电场核心素养物理观念科学思维1.推导点电荷的电场强度公式。

2.知道电场强度的叠加原理，并能应用这一原理进行简单的计算。

3.知道匀强电场及其电场线的特点。

通过场强叠加原理，更加熟悉矢量的合成法则——平行四边形定则。

知识点一点电荷的电场1.计算公式：E＝k Qr2(Q为场源电荷的电荷量)。

2.方向：当Q为正电荷时，E的方向沿Q与该点的连线向外，背离Q，当Q为负电荷时，E的方向沿Q与该点的连线向内，指向Q。

[思考判断](1)A、B两个异号电荷，A受到B的吸引力是因为A电荷处于B产生的电场中。

(√)(2)以点电荷为球心的球面上各点电场强度处处相同。

(×)(3)公式E＝Fq与E＝kQr2中q与Q含义不同。

(√)知识点二场强叠加原理1.如果有多个电荷同时存在，电场中任一点的电场强度等于这些点电荷各自在该点产生电场强度的矢量和，这个结论称为场强叠加原理。

2.若已知电荷分布，就可以求出电场中某点电场强度矢量叠加后的总强度。

[思考判断](1)电场强度是矢量，电场强度的叠加遵循平行四边形定则。

(√)(2)如果几个电场强度在同一直线上，其合场强为它们的大小之和。

(×)知识点三匀强电场1.定义：电场强度的大小和方向处处相同的电场。

2.电场线是间距相等的平行直线。

[思考判断](1)如果某空间中的电场线是直线，那么在同一条电场线上各处的场强相同。

(×) (2)匀强电场的电场线可以是曲线。

(×)在计算式E ＝kQr 2中，r →0时，电荷量为Q 的物体就不能看成是点电荷了，电场强度E 不可以认为无穷大。

研究均匀带电球体(或球壳)在球外产生的电场时，可以认为全部电荷集中在球心。

等量异种点电荷 等量同种正点电荷匀强电场的表示核心要点点电荷的电场 匀强电场[要点归纳] 1.点电荷的电场(1)E ＝k Q r 2是真空中点电荷场强的决定式，E ∝Q ，E ∝1r 2。

Q 为产生电场的场源电荷所带电荷量，r 为电场中某点与场源电荷间的距离。

电场与电势的计算方法在电学领域，电场和电势是两个重要的概念。

电场描述了电荷在空间中产生的力的作用，而电势则是描述了电荷在电场中所具有的能量状态。

了解电场和电势的计算方法对于理解和解决电学问题非常重要。

本文将介绍电场和电势的计算方法，并为读者提供实用的应用示例。

一、电场的计算方法电场是描述电荷在空间中产生的力对其他电荷的作用的物理量。

通常用电场强度来表示，它的计算方法如下：1. 对于点电荷的电场计算对于一个带电粒子，比如正电荷q1，它产生的电场强度E在距离r处的大小可以通过库仑定律计算得到：E = k * q1 / r^2其中，k为库仑常数，近似值为9×10^9 N•m^2/C^2。

电场的方向则是从正电荷指向测试点的方向。

2. 对于多个点电荷的电场计算对于多个点电荷，每个点电荷产生的电场强度可以通过叠加原理进行计算。

即将每个点电荷的电场强度矢量按照矢量相加的方式求和。

3. 对于连续分布电荷的电场计算公式如下：E = ∫ (k * dq) / r^2其中，dq表示电荷微元，通过对电荷分布的密度函数进行积分可以得到总的电场强度。

在实际应用中，可以使用数值模拟的方法来进行连续分布电荷的电场计算。

二、电势的计算方法电势是描述电荷在电场中具有的能量状态的物理量。

电势的计算方法如下：1. 对于点电荷的电势计算对于一个带电粒子，比如正电荷q1，它在距离r处的电势V可以通过库仑定律计算得到：V = k * q1 / r其中，k为库仑常数。

2. 对于多个点电荷的电势计算对于多个点电荷，每个点电荷产生的电势可以通过叠加原理进行计算。

即将每个点电荷的电势按照标量相加的方式求和。

3. 对于连续分布电荷的电势计算如下：V = ∫ (k * dq) / r其中，dq表示电荷微元，通过对电荷分布的密度函数进行积分可以得到总的电势。

在实际应用中，可以使用数值模拟的方法来进行连续分布电荷的电势计算。

三、电场和电势的应用示例1. 平行板电容器的电场和电势平行板电容器是电学中常见的电路元件，其中两个平行金属板之间填充了绝缘体介质。

点电荷的电场线和等势线解析根据库仑定律，一试验电荷q 0与点电荷Q 相距为r 时，受到的静电力为F ＝kQq 0r 2 其中k 是静电力常量，k = 9×109N·m 2/C 2。

根据电场强度的定义，点电荷Q 在r 处产生的电场强度大小为E ＝F q 0＝kQ r 2 可见：点电荷的带电量Q 越大，在周围空间产生的场强越大；场强与距离的平方成反比。

如果Q 是正电荷，场强方向沿着径向向外；如果Q 是负电荷，场强方向沿着径向向内。

以无穷远处为电势零点，取一条从r 到无穷远处的电场线为积分路径，点电荷在r 处的电势为U ＝ E ⋅ⅆs ∞0＝ E ⅆr ∞0＝kQ r 2ⅆr ∞0＝kQ r可见：点电荷的电势与距离成反比。

图示点电荷的电场线是以点电荷为端点的射线。

对于正的点电荷，射线从点电荷射向四周；对于负的点电荷，射线从四周射向点电荷。

在点电荷的平面上，点电荷的等势线是以点电荷为中心的圆，相邻两个等势线之间的电势差应该相等。

不论是正电荷还是负电荷，场点离电荷距离越近，电场线越密，等势线也越密，场强越大。

注：上图的格式是emf，编辑有所不便，在此图基础上进行转换，如下图：算法为了计算数值，取某一点的距离r0作为参考距离，也就是距离的单位，则电场强度大小可表示为E＝kQr02(r/r0)2＝E0r*2其中，r*=r/r0，是无量纲的距离或约化距离；E0=kQ/r02是r0处的场强大小。

取E0为场强单位，E/E0就是无量纲的场强或约化场强。

显然：点电荷的无量纲场强E/E0与无量纲的距离的平方成反比。

电势可表示为U＝kQr0(r/r0)＝U0r*其中，U0=kQ/r0，是r0处的电势。

取U0为电势单位，U/U0是无量纲的电势或约化电势，与无量纲的距离成反比。

等势线通常用等值线指令contour绘制，由于点电荷的等势线是同心圆，也可用矩阵画线法绘制。

由于点电荷的电场线是射线，所以用箭杆指令quiver绘制比较简单。

电场的概念及点电荷电场强度的计算2.1 电场的概念及点电荷电场强度的计算1、电场的定义2、点电荷电场强度的计算1、电场的定义(1) 什么是电场？这种存在于电荷周围，能对其他电荷产生作用力的特殊的物质称为电场。

可见电荷是产生电场的源。

(2) 电场强度的定义单位正电荷在电场中某点受到的作用力称为该点的电场强度。

电场强度严格的数学表达式为：0limt q tFE q →=21122120214πR q q F a R ε=(3) 库仑定律1q 2q 21R 其中：为真空中介电常数。

0ε91201108.851036πε--=?=?F/m2. 电场强度的计算20?4πRq E a Rε=其中：是源电荷指向场点的方向。

?R a ——点电荷电场强度的计算公式0limt q tFE q →=qtq R由库仑定律：20?4πtR qq F a Rε=电场强度定义：可得：例：在直角坐标系中，设一点电荷q 位于点，计算空间点的电场强度。

(5,3,4)P (3,2,2)P 'P 'Pr 'r Rxyzo解：如图,点电荷的电场强度为322x y z r aa a '=++534x y z r aa a =++20?4πRq E a Rε=其中：212?||3x y z R aa a R a R ++==222||2123R R ==++=所以:02124π27x y z aa a q E ε++=?212x y z R r r aa a '=-=++(3,2,2)P '(5,3,4)P r 'rRxyzo则:结论：()()()()()()3/2222104ni x i y i z i i i i i x x ay y a z z a q E x x y y z z ='''-+-+-=πε??'''-+-+-??∑在直角坐标系中，若源电荷所在点的坐标为，场点P 的坐标为，则P 点的电场强度为：q (,,)x y z '''(,,)x y z 3322200()()()4π||4π()()()x y zx x a y y a z z a q R q E R x x y y z z εε??'''-+-+-??=?=??'''-+-+-??多个点电荷产生的电场：如果有多个点电荷源,场域中某点的电场强度应该是所有点电荷在该场中产生的电场强度的矢量和。

一、场强分布图
点电荷的电场线
等量异种点电荷电场线等量同种正电荷电场线
二、列表比较
孤立的正点电荷电场
线
直线，起于正电荷，终止于无穷远。

场强
离场源电荷越远，场强越小；与场源电荷等距的各点组成的球面上场强大小相等，方向不同。

电势
离场源电荷越远，电势越低；与场源电荷等距的各点组成的球面是等势面，每点的电势为正。

等势
面
以场源电荷为球心的一簇簇不等间距的球面，离场源电荷越近，等势面越密。

孤立的负点电荷电场
线
直线，起于无穷远，终止于负电荷。

场强
离场源电荷越远，场强越小；与场源电荷等距的各点组成的球面上场强大小相等，方向不同。

电势
离场源电荷越远，电势越高；与场源电荷等距的各点组成的球面是等势面，每点的电势为负。

等势
面
以场源电荷为球心的一簇簇不等间距的球面，离场源电荷越近，等势面越密。

等量同种负点电荷电场
线
大部分是曲线，起于无穷远，终止于负电荷；有两条电场线是直线。

电势每点电势为负值。

连
线
上
场强
以中点最小为零；关于中点对称的任意两点场强大小相等，方向相反，都是背离中点；由连线的
一端到另一端，先减小再增大。

电势
由连线的一端到另一端先升高再降低，中点电势最高不为零。

中
垂
线
上
场强
以中点最小为零；关于中点对称的任意两点场强大小相等，方向相反，都沿着中垂线指向中点；
由中点至无穷远处，先增大再减小至零，必有一个
位置场强最大。

电势中点电势最低，由中点至无穷远处逐渐升高至零。

点电荷的电场 (选修3-1第一章：静电场的第三节电场强度)★★★★○○○1、点电荷周围的电场 （1）公式：2rQ kE （2）适用条件：（1）真空；（2）点电荷。

（3）由场源电荷Q 和场源电荷到该点的距离r 共同决定2、正的点电荷周围的场强方向都是由正电荷指向外；负的点电荷周围的场强方向都是指向负电荷。

等量点电荷的电场强度的比较 比较项目等量异种点电荷等量同种点电荷电场线分布图连线中点O 处的场强最小，指向负电荷一方为零连线上的场强大小(从左到右) 沿连线先变小，再变大 沿连线先变小，再变大 连线上的场强方向平行于两个电荷的连线垂直于两个电荷的连线 沿中垂线由O 点向外场强大小 O 点最大，向外逐渐减小O 点最小，向外先变大后变小关于O 点对称的A 与A′、B与B′的场强等大同向等大反向（四川省宜宾市一中2020-2020学年高二上学期）如图所示，空间中A 、B 、C 三点的连线恰构成一直角三角形，且∠C＝30°，AB ＝L ，在B 、C 两点分别放置一点电荷，它们的电量分别是＋Q 与－Q(静电力常量为k)．求斜边AC 的中点D 处的电场强度．【答案】23kQL，方向水平向右。

1、(贵州省思南中学2020-2020学年高二上学期第一次月考)对于由点电荷Q 产生的电场，下列说法正确的是（ ）A. 电场强度的表达式为E=EQ，式中的Q 就是产生电场的点电荷所带电荷量 B. 在真空中，点电荷产生电场强度的表达式为E=2kQr，式中Q 就是产生电场的点电荷所带电荷量 C. 在真空中E=2kQr ，式中Q 是试探电荷所带电荷量 D. 点电荷产生电场强度的表达式E=2kQr，与是否真空无关【答案】B2、（上海市金山中学2020-2020学年高二上学期期末）如图，O 、P 、Q 三点不在一条直线上，OP<OQ ，在O 处有一正点电荷。

若P 、Q 两点的电场强度分别为E P 、E Q ，则（ ）A. E P <E Q ，且方向相同B. E P >E Q ，且方向相同C. E P <E Q ，且方向不同D. E P >E Q ，且方向不同 【答案】D【精细解读】点电荷周围的电场的方向由正点电荷指向外，可知P 与Q 点的电场强度的方向不同；由点电荷的电场强度的公式： 2QE kr，可知因为距离OP<OQ ，所以E P >E Q ，故D 正确，ABC 错误。

点电荷和点电荷系电场强度计算方法点电荷和点电荷系电场强度的计算方法是一个基本的物理学问题，可以经由电学理论解释电场内部的磁体分布。

基本原理是：一个点电荷位于空间中的某一点，周围上下左右都有电势，因此它产生出一种电场。

单位电荷q乘以充电半径r就是点电荷，在它周围空间内可以看到有一个强大的电磁场，我们可以把这种电场简称为点电荷系电场。

点电荷系电场强度就是它能够产生的电势在特定位置是多少。

每一个点电荷产生的电场强度都是由电学定律公式表达的，即：
E=kq/r^2 。

其中 E 表示电场强度，取决于单位电荷 q 的大小，k 为环境常数，r 为点电荷与监测点的距离，它是电荷间作用力的参数，该定律描述点电荷电场强度由它们之间的立体距离给出，它表明越近点电荷强度就越大，即隔着距离越远，电场强度就越弱。

由于点电荷系电场强度可以根据点电荷的参数计算出来，因此在实际应用中，可以根据需要设置多个点电荷进行测量，然后用这些数据计算出多个点电荷系电场强度的大小，这样就能够得到一个稳定的电场强度结果。

当需要计算出一个空间的电场强度时，只需将此空间离散化成许多点电荷即可计算出各个点的电场强度，最后可以计算出该空间中电场强度的完整图形。

综上所述，点电荷和点电荷系电场强度的计算方法是一个基本的物理学问题，它是从单个点电荷的参数和位置去计算电场的强度，也可以离散化地计算空间内电场强度的图形。

由此可见，这个计算方法可用
于任何按照这个方法计算的空间电场强度的实际测量和应用中，都可以取得更精确的结果。

等量的点电荷形成的电场中的场强和电势特点在等量的点电荷形成的电场中，场强表征电场的力量或效应的大小。

场强的计算公式为场强等于电荷的大小除以距离的平方。

对于等量的点电荷，它们的大小相等，因此它们在同一距离处产生的场强也是相等的。

这意味着在等量的点电荷形成的电场中，场强的大小在空间中保持均匀分布。

这是因为电场中的每个点电荷都会对周围的空间产生相同大小和方向的力，使得场强保持一致。

此外，等量的点电荷形成的电场中，场强的方向呈放射性。

场强的方向从正电荷指向负电荷，与指向统一矢量相反。

这是因为正电荷和负电荷之间存在电力线，电力线是场强的方向标志。

在等量的点电荷形成的电场中，电力线从正电荷出发，沿着放射线向外发散，指向负电荷。

由于等量的点电荷的方向是相同的，所以电力线和场强的方向也是相同的，呈放射性分布。

除了场强，另一个特点是电势。

电势是描述电场中的能量转换的量。

在等量的点电荷形成的电场中，电势的大小与电荷的大小和距离有关。

在距离电荷较远的地方，电势较小，而在距离电荷较近的地方，电势较大。

这是因为电荷会使空间中的能量分布发生变化，能量在电场中沿着电势梯度的方向传递。

在等量的点电荷形成的电场中，电势呈球对称形态，类似于一个球面。

球面上的每个点的电势是相等的，而且与距离电荷的距离成反比。

由于点电荷的大小相同，所以球面上每个点到电荷的距离相同，因此电势在整个球面上保持均匀。

此外，电势的方向是从正电荷指向负电荷的。

电势与电力线的方向相同，都是从正电荷指向负电荷。

这是因为电场中的能量转换主要是由正电荷向负电荷转移的。

综上所述，等量的点电荷形成的电场中，场强呈放射性分布，大小均匀；而电势呈球对称分布，大小与距离成反比。

这些特点揭示了等量的点电荷形成的电场的规律性和对电场中物体的作用效应。

点电荷电场的散度
电场是描述电荷相互作用的物理量，而电荷的分布情况对电场的形态和强度有着决定性的影响。

在研究电场的性质时，散度是一个十分重要的概念。

散度是一个向量场的量，描述了该向量场在一个点附近的流动性质。

在电场中，散度可以用来描述电荷的分布情况。

如果电荷在某个区域内密集分布，那么该区域内的电场散度将会很大；相反，如果电荷分布比较稀疏，那么该区域内的电场散度将会较小。

点电荷是电荷分布最简单的情形，它的电场分布具有轴对称性。

根据高斯定理，点电荷电场的散度在距离电荷很远的地方为零，因为电荷的作用只能影响其周围比较小的区域。

而在电荷附近，电场散度会很大，因为电荷会对周围区域的电场强度和方向产生较大的影响。

总之，散度是描述电场的重要概念之一，它可以很好地反映电荷分布的情况。

对于点电荷电场来说，散度的大小和位置是由电荷的性质决定的。

- 1 -。