双点电荷所形成电场的等势面分布
- 格式:docx
- 大小:447.97 KB
- 文档页数:7

电场中的电势分布与等势面电场是物质中产生的一种物理现象,它是由电荷的存在和运动引起的。
在电场中,电势分布和等势面是研究电场性质的重要概念。
一、电势分布电势是描述电场中某一点的物理量,它表示单位正电荷在该点处所具有的势能。
在电场中,电势的分布是非常重要的,它决定了电荷在电场中的运动方式。
在电场中,电势分布受电荷的分布和电场的性质所决定。
当电荷分布对称时,电势分布也会呈现对称性;当电荷分布不对称时,电势分布则会体现出不对称的特点。
在均匀电场中,电势分布是匀速变化的。
沿着电场的方向,电势由高到低逐渐降低。
通过测量电势的变化可以判断电场的方向和强弱。
电势的正负表示了电势能增加或减少的方向。
二、等势面等势面是电场中的一种特殊情况,它指的是在电场中具有相同电势值的点所构成的面。
等势面与电势线是相互垂直的。
在电场中,等势面是沿着电场的方向均匀分布的。
高于等势面上的点具有较高的电势,低于等势面上的点具有较低的电势。
等势面的密度表示了电势的变化速率。
密集的等势面表示电势的变化较快,电场的强度较大;疏松的等势面表示电势的变化较慢,电场的强度较小。
通过绘制等势面,可以更直观地了解电场的性质。
等势面在物理实验中起到了重要的作用。
例如,当需要在两个点之间传递电荷时,可以选择沿着等势面移动,这样无需克服电势的变化,从而提高传输效率。
三、电势分布与等势面的应用电势分布和等势面在物理学、工程学等领域具有广泛的应用。
在物理学中,通过研究电势分布和等势面,可以探索电场的性质,推导出电场的数学表达式,进而揭示电场与电荷的相互作用规律。
在工程学中,电势分布和等势面的研究可以为电场的设计和应用提供指导。
例如,在电势分布较强的区域可以布置电场传感器,用于检测电场强度的变化。
同时,通过控制电势分布,可以实现对电场的调节和优化,以提高电子设备的性能。
此外,在医学领域中,电势分布和等势面的研究也有一定的应用。
例如,通过检测人体表面的电势分布,可以了解身体某部位的神经活动情况,从而辅助诊断和治疗。

电势电势能电势差场强之间的关系场强(矢量)——对应的是力;电势(标量)——对应的是能;两者通过力做功——造成能量变化,而联系在一起;-------------电场线与场强的关系:电场线越密的地方表示场强越大,电场线上每点的切线方向表示该点的场强方向。
电场线与电势的关系:沿着电场线方向,电势越来越低。
电场线与等势面的关系:电场线越密的地方等势面也越密,电场线与通过该处的等势面垂直。
场强数值与电势数值无直接关系:场强大(或小)的地方电势不一定大(或小),零电势可人为选取,而场强是否为零则由电场本身决定。
从电势和电势能的关系来看:ε=Uq由于通常规定无穷远处的电势为零,正的场电荷电场中的各点电势都为正值,负的场电荷的电场中的各点电势都为负值。
这一点与检验电荷的电性和电量无关。
这样,我们知道:ε=Uq1)正的场源电荷电场中:U>0,负检验电荷在场中,电量为负值,因此它的电势能为负值;正检验电荷在场中,电量为正值,因此它的电势能为正值;2)负的场源电荷电场中:U<0,负检验电荷在场中,电量为负值,因此它的电势能为正值;正检验电荷在场中,电量为正值,因此它的电势能为负值;从电势能的特点来看,正电荷在正电荷的电场中电势能为正值,负电荷在负电荷的电场中电势能也为正值,同种电荷之间为斥力的作用,其势能为斥力势能,斥力势能大于零,相当于若规定地球上的海平面为重力势能的零点,物体在海拔高于海平面处(高山)的重力势能则为正值一样;另一方面,正电荷在负电荷的电场中电势能为负值,负电荷在正电荷电场中电势能也为负值,异种电荷之间为引力的作用,其势能为引力势能,引力势能小于零,相当于若规定地球上的海平面为重力势能的零点,物体在海拔低于海平面处(盆地)的重力势能则为负值一样。
二、电势差。
电场中两点间的电势的差值叫做电势差,即:UAB =UA-UB,UBA=UB-UA,在电场中A、B两点间移动电荷时,电场力的功等于电量q和这两点间的电势差UAB 的乘积。
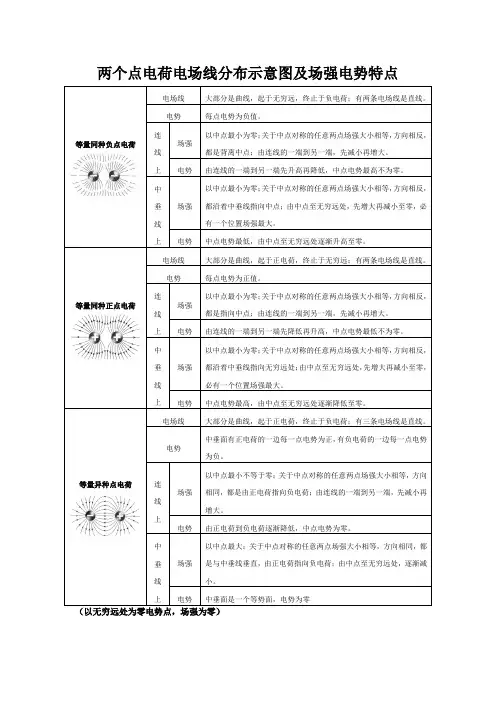
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量同种正点电荷电场线大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最高,由中点至无穷远处逐渐降低至零。
等量异种点电荷电场线大部分是曲线,起于正电荷,终止于负电荷;有三条电场线是直线。
电势中垂面有正电荷的一边每一点电势为正,有负电荷的一边每一点电势为负。
连线上场强以中点最小不等于零;关于中点对称的任意两点场强大小相等,方向相同,都是由正电荷指向负电荷;由连线的一端到另一端,先减小再增大。
电势由正电荷到负电荷逐渐降低,中点电势为零。
中垂线上场强以中点最大;关于中点对称的任意两点场强大小相等,方向相同,都是与中垂线垂直,由正电荷指向负电荷;由中点至无穷远处,逐渐减小。
电势中垂面是一个等势面,电势为零(以无穷远处为零电势点,场强为零)(以无穷远处为零电势点,场强为零)注意:电场线、等势面的特点和电场线与等势面间的关系:①电场线的方向为该点的场强方向,电场线的疏密表示场强的大小。


静电场模型一、夯实基础知识1、深刻理解库仑定律和电荷守恒定律。
(1)库仑定律:真空中两个点电荷之间相互作用的电力,跟它们的电荷量的乘积成正比,跟它们的距离的二次方成反比,作用力的方向在它们的连线上。
即:221r q kq F =其中k 为静电力常量, k =9.0×10 9 N m 2/c 2成立条件:①真空中(空气中也近似成立),②点电荷。
即带电体的形状和大小对相互作用力的影响可以忽略不计。
(这一点与万有引力很相似,但又有不同:对质量均匀分布的球,无论两球相距多近,r 都等于球心距;而对带电导体球,距离近了以后,电荷会重新分布,不能再用球心间距代替r )。
(2)电荷守恒定律:系统与外界无电荷交换时,系统的电荷代数和守恒。
2、深刻理解电场的力性质。
电场的最基本的性质是对放入其中的电荷有力的作用。
电场强度E 是描述电场的力的性质的物理量。
⑴定义:放入电场中某点的电荷所受的电场力F 跟它的电荷量q 的比值,叫做该点的电场强度,简称场强。
qFE=这是电场强度的定义式,适用于任何电场。
其中的q 为试探电荷(以前称为检验电荷),是电荷量很小的点电荷(可正可负)。
电场强度是矢量,规定其方向与正电荷在该点受的电场力方向相同。
⑵点电荷周围的场强公式是:2r kQE =,其中Q 是产生该电场的电荷,叫场源电荷。
⑶匀强电场的场强公式是:dUE =,其中d 是沿电场线方向上的距离。
3、深刻理解电场的能性质。
(1)电势φ:是描述电场能的性质的物理量。
○1电势定义为φ=qE,是一个没有方向意义的物理量,电势有高低之分,按规定:正电荷在电场中某点具有的电势能越大,该点电势越高 。
○2电势的值与零电势的选取有关,通常取离电场无穷远处电势为零;实际应用中常取大地电势为零。
○3当存在几个“场源”时,某处合电场的电势为各“场源”在此处电场的电势的代数和 。
○4电势差,A 、B 间电势差U AB =ΦA -ΦB ;B 、A 间电势差U BA =ΦB -ΦA ,显然U AB =-U BA ,电势差的值与零电势的选取无关。

两个正点电荷等势面以两个正点电荷等势面为标题,我们来探讨一下正点电荷和等势面之间的关系。
正点电荷是电荷量非常小但集中在一个点上的电荷。
正点电荷的电场是一个以该电荷为中心的球对称电场,电场强度与距离的平方成反比。
等势面是指空间中的各点在电场中具有相同电势的面。
等势面与电场线垂直,且等势面之间的电势差是恒定的。
当存在两个正点电荷时,它们之间会形成一个复杂的电场分布。
我们可以通过计算或者实验来确定两个正点电荷之间的等势面。
考虑两个正点电荷相距比较远时的情况。
假设两个正点电荷的电荷量分别为q1和q2,它们之间的距离为r。
根据库仑定律,两个电荷之间的电势差可以表示为V=k(q1/r1+q2/r2),其中k为库仑常数。
在这种情况下,等势面的形状近似为以两个正点电荷为中心的球面,且等势面的电势差随着距离的增加而逐渐减小。
接下来,考虑两个正点电荷相距比较近时的情况。
在这种情况下,由于两个正点电荷之间的相互作用较强,等势面的形状会发生变化。
具体来说,等势面会发生偏移,呈现出不规则的形状。
这是因为两个正点电荷之间的相互作用导致了电势分布的不均匀。
除了以上两种情况,当两个正点电荷的电荷量相等时,等势面的形状会更为特殊。
此时,等势面将成为一个以两个正点电荷连线的中点为中心的球面。
这是因为两个正点电荷的电势大小相等,导致了等势面的形状对称。
在实际应用中,我们可以利用等势面来研究电场的分布和特性。
例如,在电学实验中,我们可以通过在等势面上放置试验电荷来测量电场强度。
另外,等势面也可以帮助我们理解电场力线的分布规律,从而描绘出整个电场的形态。
总结起来,两个正点电荷之间的等势面与电场强度和电势分布密切相关。
通过研究等势面的形状和分布,我们可以深入理解电场的特性和行为。
这对于解决实际问题和应用电学知识具有重要意义。


等量同种点电荷的等势面在电场中,等势面是指位于同一电势的点构成的曲面。
等势面可以帮助我们理解电场分布和电势分布,并对电场中的电荷运动和电场强度的变化有重要的指导意义。
当电场中存在等量同种点电荷时,其等势面的分布情况将受电势分布的影响,下面我们将详细探讨等量同种点电荷的等势面。
等量同种点电荷在电场中的分布会导致电势分布的变化,从而形成各种不同形状的等势面。
根据库仑定律,两个等量同种点电荷之间的电势是与它们之间的距离成反比的,因此电势分布呈现出一种特定的形式。
为了更好地理解等量同种点电荷的等势面,我们可以通过数学公式和图像来进行分析和描述。
首先,我们可以利用数学公式来推导等势面的分布。
假设有两个等量同种点电荷q1和q2,它们之间的距离为r,那么它们之间的电势可以表示为V=kq1q2/r,其中k为库仑常数。
根据这个公式,我们可以得到在不同距离下的电势数值,然后将这些数值连接起来,就可以得到等势面的分布情况。
在这个过程中,我们通常会采用数值计算和图形绘制的方法来帮助我们更直观地理解等势面的形状和分布。
其次,我们可以通过图像来展示等量同种点电荷的等势面。
在电场模拟软件中,我们可以设置等量同种点电荷的参数,然后通过软件自动生成电势分布和等势面的图像。
这样我们就能够清晰地看到等势面的形状和分布情况,从而对电场中等量同种点电荷的影响有更直观的认识。
在实际的研究和教学中,等量同种点电荷的等势面往往会成为重要的教学内容和研究对象。
通过对等势面的分布进行分析和描述,可以帮助我们更深入地理解电场中电势的分布规律,从而为相关领域的研究和应用提供重要的理论基础。
总之,等量同种点电荷的等势面是电场中重要的研究对象,它对于我们理解电场分布和电势分布有着重要的指导意义。
通过数学公式和图像的分析,我们可以更好地探讨等势面的形状和分布情况,从而深入理解电场中等量同种点电荷的影响。
相信随着我们的深入研究和实践,等势面的相关理论和应用也将不断得到拓展和发展。

两个无限大平面电荷等势面
当涉及到两个无限大平面电荷的等势面时,我们需要考虑电场
的分布和电势的变化。
首先,让我们考虑两个无限大平面电荷分别
位于x-y平面上方和下方。
假设它们的电荷密度分别为σ1和σ2。
首先,我们来讨论第一个无限大平面电荷的等势面。
由于这是
一个无限大平面,电场在垂直于平面的方向上是均匀的。
因此,等
势面将是与这个平面平行的平面。
电场线将垂直于这些等势面,并
且等势面之间的距离将随着距离电荷平面的距离而变化。
接下来,我们考虑第二个无限大平面电荷的等势面。
同样,由
于这也是一个无限大平面,电场在垂直于平面的方向上是均匀的。
因此,等势面将是与这个平面平行的平面,并且电场线将垂直于这
些等势面。
当这两个无限大平面电荷彼此靠近时,它们的电场线会相互影响,并且等势面也会相互影响。
在它们之间的区域,等势面将会发
生变形,形成一种交错的模式,以适应两个电场的影响。
这些变形
的等势面将呈现出一种复杂的图案,反映了两个电场的相互作用。
总的来说,两个无限大平面电荷的等势面将呈现出一种复杂的交错模式,反映了它们之间相互作用的电场线的影响。
这种模式在数学上可能比较复杂,但可以通过计算来确定这些等势面的具体形状和分布。

电场在等位面上的电势分布导言:电势(potential)是描述电场中空间各点电势能的物理量。
电势分布是指空间中各点的电势数值分布情况。
在等位面上,表示电势相等的点构成一条曲线,被称为等位线。
本文将探讨电场在等位面上的电势分布及其特点。
一、电势的定义与计算电势是描述电场的一种性质,指的是单位正电荷在某处所具有的电势能。
电势可以通过以下公式进行计算:\[V=\frac{U}{q}\]其中,V表示电势,U表示电势能,q表示单位正电荷。
在电场中,电势随着距离的变化而改变,从而形成了不同点的电势分布。
二、电场在等位面上的特点1. 等位线的定义等位线是指一组在同一等势位上的点构成的曲线。
等势位是一组电势相等的点所在的平面或曲面,被称为等位面。
电场在等位面上的电势分布是描述电势在等位面上的变化情况。
2. 等位线的性质(1)等位线与电场线垂直相交在电场中,电场线表示电场的方向和强度。
等位线与电场线垂直相交,这是因为等位线所表示的点处具有相同电势,而电场线的方向是电场力的方向,两者之间垂直交叉。
(2)等位线的间距在等势面上,等位线的间距越小,表示电势变化越剧烈;间距越大,表示电势变化越缓慢。
在电势分布中,等位线的间距可以反映电场中电势的变化情况。
(3)等位线的曲率等位线一般具有曲率,曲率的大小反映了电势变化的速率。
曲率大的地方,电势变化剧烈;曲率小的地方,电势变化缓慢。
曲率可以通过等位线的弯曲程度来描述。
三、电势分布的实例以两个平行带电板构成的均匀带电场为例,来探讨电势分布在等位面上的表现。
带电板1带正电荷,带电板2带负电荷,它们之间的距离为d。
在两板中间的某一水平面上,构成了一个等势面。
这个等势面是垂直于带电板的平面,带电板上各点电势相等。
在该等势面上,靠近正带电板的区域电势较大,远离正带电板的区域电势较小。
等位线由电势相等的点构成,可以看做离正带电板越远,等位线密度越小;离正带电板越近,等位线密度越大。
同样,离负带电板越近的地方,等位线密度越大;离负带电板越远的地方,等位线密度越小。

两个不等量同种点电荷电场线和等势面
不等量同种点电荷产生的电场线和等势面在形状上会有很大的差异。
首先,电场线是描述电场强度的线条,而等势面是描述电场势能相等的面。
电场线是垂直于等势面的,因为电场线代表电场的方向,而电场的方向和力的方向是垂直的。
所以电场线和等势面是相交的,但不重合。
对于不等量的同种点电荷,电场线的形状会受到电荷的量的影响。
电荷量越大,电场线越密集。
电场线从正电荷向外辐射,而从负电荷指向内部。
因此,在正电荷附近,电场线会从电荷向外散开;在负电荷附近,电场线会从外部汇聚到电荷。
而在两个不等量点电荷之间的区域,电场线会趋向于沿着电荷间连接线的直线方向排列。
而等势面的形状则与电荷的量无关。
等势面是电场势能相等的面,所以等势面上的每一点上的电势相同。
对于同种电荷,等势面是以电荷为中心的球面,且球面越接近电荷,电势越高。
综上所述,两个不等量同种点电荷产生的电场线和等势面在形状上会有所差异,电场线的形状受电荷量的影响,而等势面主要以球面形式存在。
电场(一)-----两个点电荷专题一:两个静止的带相等电荷量的点电荷-----同种电荷注意:两个带相等电荷量的同种电荷连线的中点合场强最小,等于零,中垂线上的合场强方向沿中垂线方向。
练习题:1.两个带等量正电的点电荷Q1和Q2的等势面分布如图所示,a、b、c、d为电场中的四个点,其中b、c两点关于两电荷连线对称,a、d两点在两电荷连线上,且a点到Q1的距离和d 点到Q2的距离相等。
则()A.b点的场强与c点的场强相同B.a点的场强比d点的场强大C.a点的电势比b点的电势高D.电子在a点的电势能比在c点的电势能大2.如图所示,A、B为两个等量正点电荷连线上的两点(其中B为连线中点),C为连线中垂线上的一点。
今将一带负电的试探电荷自A沿直线移到B再沿直线移到C。
下列说法中正确的是()A.B点的场强比C点的场强大B.A点的电势比C点的电势高C.从A点移到B点的过程中,电场力对该试探电荷做正功D.从B点移到C点的过程中,该试探电荷的电势能保持不变专题二:两个静止的带相等电荷量的点电荷-----异种电荷注意:两个带相等电荷量的异种电荷连线的中点合场强最大,等于=k,中垂线上的合场强方向与中垂线垂直。
(r 为点电荷到重点的距离。
)1.图示平面内固定两个等量异种点电荷,M 、N 两点关于两电荷的连线对称,M 、P 两点关于两电荷连线的中垂线对称。
下列说法正确的是()A .M 、P 两点的电场强度相同B .N 、P 两点的电场强度相同C .N 、P 两点的电势相等D .电子在M 点的电势能比在N 点的大2.如图所示,O 为等量异种点电荷连线的中点,A 、B 为连线上的点,C 、D 为其中垂线上的点,且A 、B 、C 、D 距O 点距离相等,取无穷远处的电势为零。
下列说法正确的是()A.A 、B 两点电势相等B.C 、D 两点电场强度不相同C.O 点电势为零,电场强度也为零D.沿中垂线移动电荷,静电力始终不做功3.如图所示,真空中两个等量异号的点电荷Q -和Q +分别位于A 点和A '点,以AA '连线中点O 建立空间直角坐标系O xyz -,B 、C 、M 、P 是坐标轴上的4个点,其中BO OC =。
四个等势面电场模型电场是物理学中的一个重要概念,用来描述电荷之间的相互作用。
在电场中,电荷会受到电场力的作用,从而产生运动或发生其他变化。
为了更好地理解电场的分布情况,科学家们提出了各种电场模型。
本文将介绍四个等势面电场模型,分别是均匀电场、点电荷电场、电偶极子电场和导体表面电场。
一、均匀电场均匀电场是指电场强度在空间中保持恒定的电场。
在均匀电场中,电场线是平行且等距离分布的,等势面则是垂直于电场线的平面。
这种电场模型常见于两个平行金属板之间的电场分布,如平行板电容器。
在平行板电容器中,两个平行金属板上的电荷分布均匀,形成了一个均匀电场。
二、点电荷电场点电荷电场是指由一个电荷点产生的电场。
在点电荷电场中,电荷点周围的电场强度呈放射状分布,电场线从正电荷指向负电荷。
等势面则是以电荷点为中心的等距离球面。
这种电场模型常见于电荷之间的相互作用,如原子核周围的电子云。
三、电偶极子电场电偶极子电场是指由一个正电荷和一个负电荷之间形成的电场。
在电偶极子电场中,电场线从正电荷指向负电荷,电场强度在两个电荷之间较强,两个电荷之外则较弱。
等势面则呈现出类似于电偶极子的形状,即两个电荷之间的等距离椭圆。
这种电场模型常见于分子中的电荷分布,如水分子中的氧原子和氢原子。
四、导体表面电场导体表面电场是指位于导体表面的电场分布。
在导体表面电场中,电场线与导体表面垂直,并且电场强度在导体表面处于最大值。
等势面则与导体表面平行,并且等势线之间的间距相等。
这种电场模型常见于导体的静电平衡状态,如金属外壳中的电荷分布。
通过以上四个等势面电场模型的介绍,我们可以更好地理解电场的分布情况。
均匀电场、点电荷电场、电偶极子电场和导体表面电场分别适用于不同的场景,但都遵循电场线与等势面的垂直关系。
这些电场模型为我们研究电场提供了有力的工具,帮助我们更好地理解电荷之间的相互作用。
在实际应用中,我们可以根据需要选择适当的电场模型来描述和分析电场问题,从而更好地应用电场理论解决实际问题。
常见电场电场线分布规律————————————————————————————————作者:————————————————————————————————日期:常见电场电场线分布规律电场强度、电场线、电势部分基本规律总结整理:胡湛霏一、几种常见电场线分布:二、等量异种电荷电场分析1、场强:①在两点电荷连线上,有正电荷到负电荷,电场强度先减小后增大,中点O的电场强度最小。
电场强度方向由正电荷指向负电荷;②两点电荷的连线的中垂线上,中点O的场强最大,两侧场强依次减小。
各点电场强度方向相同。
2、电势:①由正电荷到负电荷电势逐渐降低;②连线的中垂线所在的、并且与通过的所有电场线垂直的平面为一等势面;③若规定无限远处电势为0,则两点电荷连线的中垂线上各点电势即为0。
3、电势能:(设带电粒子由正电荷一端移向负电荷一端)①带电粒子带正电:电场力做正功,电势降低,电势能减少;②带电粒子带负点:电场力做负功,电势降低,电势能增加。
三、等量同种电荷电场分析1、场强:①两点电荷的连线上,由点电荷起,电场强度越来越小,到终点O的电场强度为0,再到另一点电荷,电场强度又越来越大;②两点电荷连线的中垂线上,由中点O向两侧,电场强度越来越大,到达某一点后电场强度又越来越小;③两点电荷(正)连线的中垂线上,电场强度方向由中点O指向外侧,即平行于中垂线。
2、电势:①两正点电荷连线上,O点电势最小,即由一个正点电荷到另一正点电荷电势先降低后升高。
连线的中垂线上,O电电势最大,即O点两侧电势依次降低。
②两负点电荷连线上,O点电势最大,即由一个负点电荷到另一负点电荷电势先增高后降低。
连线的中垂线上,O点电势最小,即O点两侧电势依次升高。
③其余各点电势由一般规律判断,顺着电场线方向电势逐渐降低。
3、电势能:①由电势判断:若带电粒子为正电荷,则电势越高,电势能越大;若带电粒子为负电荷,则电势越高,电势能越小。
②由功能关系判断:若电场力做负功,则电势能增加;若电势能做正功,则电势能减少。
等量“双电荷”电场线和等势面的分布特点及应用一、等量“双电荷”电场线和等势面的分布特点图一、图二分别为等量异种电荷和等量同种电荷(以正电荷为例)的电场线和等势面分布图。
由图我们可以得出下述结论:1. 它们都是关于两电荷连线及其中垂线对称分布的空间立体图形。
2. 电场线与等势面垂直,电场线从电势高的等势面指向电势较低的等势面。
在图中找两个点,我们可以比较它们的电势的高低,也可以判断在这两点间移动电荷时电场力的做功情况。
(图一)3. 越靠近电荷,电场线越密,场强越强,运用这一点我们可以比较其中两点场强的大小。
4. 等量异种电荷,其连线上场强先减小后增大,中点最小但不为零,电势由高到低。
它们连线的中垂线上,电势相等,都为零(取无穷远处电势为零,下同);而场强由中点向两侧到无穷远,不断减小,到无穷远处为零。
可以看到,电势相等处,场强不一定相等。
(图二)5. 两个带等量正电荷的点电荷,其连线中点处的合场强等于零;但电势不等于零。
此点就是一个场强为零而电势不为零的实例。
连线的中垂线上的电场线指向无穷远处,说明电势不断降低,到无穷远处为零;而场强由零先增大后减小,到无穷远处也为零。
由此可见,电势为零,场强也同为零。
二、“双电荷”电场线和等势面分布特点的应用3. 等量异种点电荷的连线和其中垂线如图五所示,现将一个带负电的检验电荷先从图中a点沿直线移到b点,再从b点沿直线移到c点。
则检验电荷在此全过程中A .所受电场力的方向将发生改变B. 所受电场力的大小恒定C. 电势能一定减小D. 电势能先不变后减小4. 如图六所示,水平平面内有两个点电荷A和B,带等量正电荷Q,在点电荷A、B连线的中垂线上某点P由静止释放一电子,试分析电子运动情况及能量转化情况。
5. 如图七所示,一电子沿等量异种电荷的中垂线由A-O-B匀速飞过,则电子除受电场力外,所受的另一个力的大小变化和方向的情况是A .先变大后变小,B. 先变大后变小,C. 先变小后变大,D. 先变小后变大,6. 如图八所示,A、B的平面上,对称地在A、B之间取a、b、c、d四点。
双点电荷所形成电场的等势面分布
崔丽波
双点电荷所形成的的电场是我们在高中阶段学习过的一种物理模型,我们当时对这个模型只做过定性分析,只是大概的了解了空间里的一些等势面电场线分布情况,一些具体的细节我们不明究竟,现在通过MATLAB软件我们可以清楚的描绘出此模型的电场分布情况,让我们再来深刻认识一下这个模型。
要了解空间的电场分布情况,我们可以先把等势面分布情况想清楚了,通过等势面上的电场线与等势面垂直,很容易就可以画出电场线的分布情况,所以重点在于判断空间的等势面分布情况。
下面我们分别来看看可能会出现的一些情况:
等量异种电荷的等势面分布
此种情况我们关注的重点应该在两点电荷的中垂线上,在这条线上电
势为0,场强方向为水平。
等量同种电荷的等势面分布
此种情况我们关注的重点在两点电荷连线的中心处,此处是一个奇点,等势面相交,场强为0,通过场强方向垂直于等势面的结论,我们可以想象一下,此点附近场强比较奇怪。
非等量同种电荷等势面分布
此种情况同等量同种电荷类似,不同的是奇点位置向电量小的偏移。
非等量异种电荷等势面分布(左正右负,正大负小)此种情况较为特殊,我们来详细介绍一下。
我们先来看两个特殊的位置:下图中蓝色为电势为0的等势面,红色等势面的两个部分在一处相交,相交处场强为0,大圈向外电势逐渐降低,小圈向里电势也逐渐降低。
电势为0和正值的等势面是这样的:
电势为0和负值的等势面是这样的:
然后组合到一起就是我们上面看到的等势面分布。