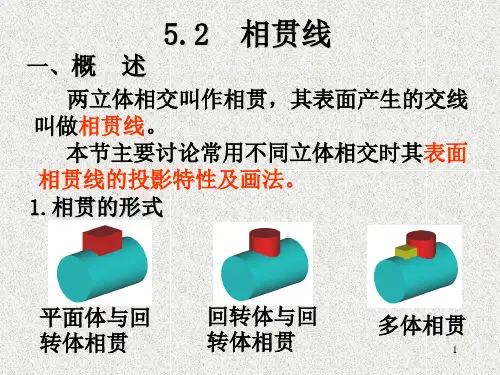
9.1 两平面立体相贯9.2 同坡屋面9.3 平面立体与曲面立体相贯9.4 两曲面立体相贯9.5 常见曲面立体相贯线的讨论两立体相交，也称两立体相贯，它们表面的交线称为相贯线。
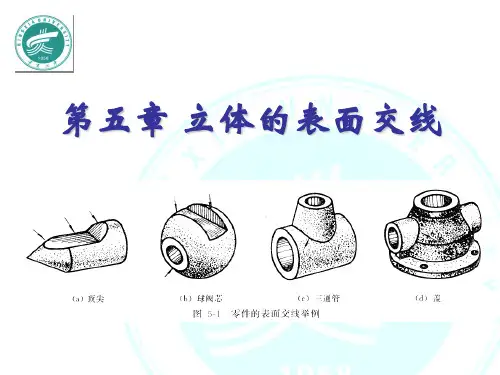
工程形体一般是多种几何形体的组合，当这些基本几何体表面相交时，会产生相贯线。
相贯线是几何体表面的分界线。
在绘制工程形体的视图时，需要画出相贯线的投影。
坝体与闸墩之间、进水口处、两廊道相交处均有相贯线。
立体与立体相贯可分为三种情况：(1)两平面立体相交。
(2)平面立体与曲面立体相交。
(3)两曲面立体相交。
由于立体的形状、大小及相互位置的不同，相贯线的形状也各不相同，可能是直线段或平面曲线段的组合，也可能是空间曲线。
但是，所有相贯线都有下列基本性质：1. 相贯线是相交两立体表面的共有线，它的投影必在两立体投影重叠部分的范围以内；2. 由于立体有一定的范围，所以相贯线一般是封闭的；3. 相贯线是相交立体表面间的分界线，每个参加相交的立体的轮廓线都不能穿过相贯线而进入另一立体内部。
当一立体全部棱线或素线与另一立体表面相交时称为全贯，全贯时一般有两条相贯线；当两立体都只有部分棱线或素线与另一立体表面相交时称为互贯，互贯时则只有一条相贯线。
求相贯线实质上是求两立体表面一系列共有点，然后依次光滑连接，并判别可见性。
一般地说这些共有点是一个立体的素线与另一立体表面的交点，也称为贯穿点。
求相贯线的步骤一般如下：1.分析两立体的相对位置及其相对于投影面的位置；2.分析相贯线的性质——空间形状及投影情况，选择解题方法；3.求相贯线上的控制点及中间点。
控制点包括：轮廓线（棱线）上的点，极限位置点——最高最低点、最左最右点、最前最后点，相贯线端点，曲线特征点（如椭圆的长短轴端点、曲线的拐点等）；4.根据相贯线的性质依次连接所求各点；5.区别相贯线各段的可见性，并补全立体的投影。
判别相贯线可见性的原则只有位于两形体都可见的表面上的交线，是可见的。
只要有一个表面不可见，则交线就不可见。
