冀教版八年级上16.2 线段的垂直平分线 能力培优训练(含答案)

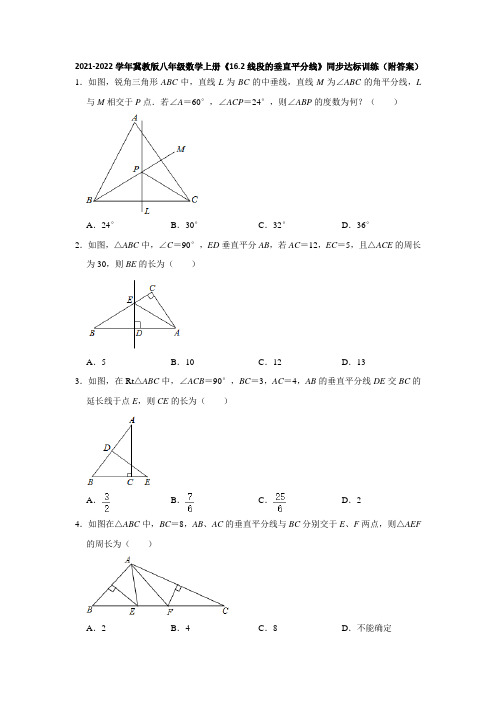
2021-2022学年冀教版八年级数学上册《16.2线段的垂直平分线》同步达标训练（附答案）1．如图，锐角三角形ABC中，直线L为BC的中垂线，直线M为∠ABC的角平分线，L 与M相交于P点．若∠A＝60°，∠ACP＝24°，则∠ABP的度数为何？（）A．24°B．30°C．32°D．36°2．如图，△ABC中，∠C＝90°，ED垂直平分AB，若AC＝12，EC＝5，且△ACE的周长为30，则BE的长为（）A．5B．10C．12D．133．如图，在Rt△ABC中，∠ACB＝90°，BC＝3，AC＝4，AB的垂直平分线DE交BC的延长线于点E，则CE的长为（）A．B．C．D．24．如图在△ABC中，BC＝8，AB、AC的垂直平分线与BC分别交于E、F两点，则△AEF 的周长为（）A．2B．4C．8D．不能确定5．已知：如图，在△ABC中，边AB的垂直平分线分别交BC、AB于点G、D，若△AGC 的周长为31cm，AB＝20cm，则△ABC的周长为（）A．31cm B．41cm C．51cm D．61cm6．如图，△ABC中，∠A＝70°，点O是AB、AC垂直平分线的交点，则∠BCO的度数是（）A．40°B．30°C．20°D．10°7．如图，DE是△ABC中AC边的垂直平分线，若BC＝6cm，AB＝8cm，则△EBC的周长为（）A．14cm B．18cm C．20cm D．22cm8．如图，在△ABC中，AB、AC的垂直平分线l1、l2相交于点O，若∠BAC等于82°，则∠OBC等于（）A．8°B．9°C．10°D．11°9．如图，已知AD是△ABC的角平分线，AD的中垂线交AB于点F，交BC的延长线于点E．以下四个结论：（1）∠EAD＝∠EDA；（2）DF∥AC；（3）∠FDE＝90°；（4）∠B ＝∠CAE．恒成立的结论有（）A．（1）（2）B．（2）（3）（4）C．（1）（2）（4）D．（1）（2）（3）（4）10．在△ABC中，∠ABC＝45°，AD，BE分别为BC、AC边上的高，AD、BE相交于点F，下列结论：①∠FCD＝45°，②AE＝EC，③S△ABF：S△AFC＝BD：CD，④若BF＝2EC，则△FDC周长等于AB的长．正确的是（）A．①②B．①③C．①④D．①③④11．如图，在△ABC中，DE是AC的垂直平分线，分别交BC，AC于点D，E，连接AD，若△ABD的周长C△ABD＝16cm，AB＝5cm，则线段BC的长度等于（）A．8cm B．9 cm C．10 cm D．11 cm12．如图，在Rt△ABC中，∠ACB＝90°，BC＝3，AC＝4，AB的垂直平分线DE的延长线于点E，则DE的长为（）A．B．C．D．13．如图地面上有三个洞口A、B、C，老鼠可以从任意一个洞口跑出，猫为能同时最省力地顾及到三个洞口（到A、B、C三个点的距离相等），尽快抓到老鼠，应该蹲守在（）A．△ABC三边垂直平分线的交点B．△ABC三条角平分线的交点C．△ABC三条高所在直线的交点D．△ABC三条中线的交点14．如图，在△ABC中，AB边的中垂线DE，分别与AB边和AC边交于点D和点E，BC 边的中垂线FG，分别与BC边和AC边交于点F和点G，又△BEG周长为16，且GE＝1，则AC的长为（）A．13B．14C．15D．1615．如图所示，在△ABC中，内角∠BAC与外角∠CBE的平分线相交于点P，BE＝BC，PB 与CE交于点H，PG∥AD交BC于F，交AB于G，连接CP．下列结论：①∠ACB＝2∠APB；②S△P AC：S△P AB＝AC：AB；③BP垂直平分CE；④∠PCF＝∠CPF．其中，正确的有（）A．1个B．2个C．3个D．4个16．如图，△ABC中，D是AB的中点，DE⊥AB，∠ACE+∠BCE＝180°，EF⊥AC交AC 于F，AC＝12，BC＝8，则AF＝．17．如图，在△ABC中，∠B＝40°，∠C＝45°，AB的垂直平分线交BC于点D，AC的垂直平分线交BC于点E，则∠DAE＝．18．如图，线段AB、BC的垂直平分线l1、l2相交于点O，若∠1＝39°，则∠AOC＝．19．如图，在△ABC中，AC＝BC＝2，∠C＝90°，AD是△ABC的角平分线，DE⊥AB，垂足为E，AD的垂直平分线交AB于点F，则△DEF的面积为．20．如图，△ABC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．若∠A＝60°，∠ACF＝48°，则∠ABC的度数为．21．如图，△ABC中，BC的垂直平分线DP与∠BAC的角平分线相交于点D，垂足为点P，若∠BAC＝85°，则∠BDC＝．22．如图，已知AE＝BE，DE是AB的垂直平分线，BF＝12，CF＝3，则AC＝．23．如图，在△ABC中，AB边的垂直平分线l1交BC于点D，AC边的垂直平分线l2交BC 于点E，l1与l2相交于点O，连接OB，OC，若△ADE的周长为6cm，△OBC的周长为16cm．（1）求线段BC的长；（2）连接OA，求线段OA的长；（3）若∠BAC＝120°，求∠DAE的度数．24．如图，Rt△ABC中，∠ACB＝90°，D是AB上一点，BD＝BC，过点D作AB的垂线交AC于点E，求证：BE垂直平分CD．25．已知△ABC中，AD是∠BAC的平分线，AD的垂直平分线交BC的延长线于F．求证：∠BAF＝∠ACF．26．如图，在△ABC中，∠A＝60°，点D是BC边的中点，DE⊥BC，∠ABC的角平分线BF交DE于△ABC内一点P，连接PC．（1）若∠ACP＝24°，求∠ABP的度数；（2）若∠ACP＝m°，∠ABP＝n°，请直接写出m，n满足的关系式．参考答案1．解：∵直线M为∠ABC的角平分线，∴∠ABP＝∠CBP．∵直线L为BC的中垂线，∴BP＝CP，∴∠CBP＝∠BCP，∴∠ABP＝∠CBP＝∠BCP，在△ABC中，3∠ABP+∠A+∠ACP＝180°，即3∠ABP+60°+24°＝180°，解得∠ABP＝32°．故选：C．2．解：∵ED垂直平分AB，∴BE＝AE，∵AC＝12，EC＝5，且△ACE的周长为30，∴12+5+AE＝30，∴AE＝13，∴BE＝AE＝13，故选：D．3．解：∵∠ACB＝90°，BC＝3，AC＝4，根据勾股定理得：AB＝5，而AB的垂直平分线DE交BC的延长线于点E，∴∠BDE＝90°，∠B＝∠B，∴△ACB∽△EDB，∴BC：BD＝AB：（BC+CE），又∵BC＝3，AC＝4，AB＝5，∴3：2.5＝5：（3+CE），从而得到CE＝．解法二：连接AE．∵DE垂直平分线段AB，∴AE＝BE，设AE＝BE＝x，则EC＝x﹣3，在Rt△ACE中，∵AE2＝AC2+EC2，∴x2＝42+（x﹣3）2，解得x＝，∴EC＝﹣3＝．故选：B．4．解：∵AB的中垂线交BC于E，AC的中垂线交BC于F，∴EA＝EB，F A＝FC，则△AEF的周长＝AE+EF+AF＝BE+EF+FC＝BC＝8，故选：C．5．解：∵DG是AB的垂直平分线，∴GA＝GB，∵△AGC的周长为31cm，∴AG+GC+AC＝BC+AC＝31cm，又AB＝20cm，∴△ABC的周长＝AB+AC+BC＝51cm，故选：C．6．解：连接OA、OB，∵∠BAC＝70°，∴∠ABC+∠ACB＝110°，∵O是AB，AC垂直平分线的交点，∴OA＝OB，OA＝OC，∴∠OAB＝∠OBA，∠OCA＝∠OAC，OB＝OC，∴∠OBA+∠OCA＝70°，∴∠OBC+∠OCB＝110°﹣70°＝40°，∵OB＝OC，∴∠BCO＝∠CBO＝20°，故选：C．7．解：∵DE是△ABC中AC边的垂直平分线，∴AE＝CE，∴CE+BE＝AB＝8cm．∵BC＝6cm，∴△EBC的周长＝BC+CE+BE＝BC+AB＝6+8＝14（cm）．故选：A．8．解：连接OA，∵∠BAC＝82°，∴∠ABC+∠ACB＝180°﹣82°＝98°，∵AB、AC的垂直平分线交于点O，∴OB＝OA，OC＝OA，∴∠OAB＝∠OBA，∠OAC＝∠OCA，∴∠OBC+∠OCB＝98°﹣（∠OBA+∠OCA）＝16°，∴∠OBC＝8°，故选：A．9．解：（1）∵EF是AD的垂直平分线，∴EA＝ED，F A＝FD，又∵EF＝EF，∴△AEF≌△DEF（SSS），∴∠AEF＝∠DEF，又∵AD⊥EF，∴∠EAD＝∠EDA；（2）∵EF是AD的垂直平分线，∴F A＝FD，∴∠FDA＝∠F AD，∵AD平分∠BAC，∴∠F AD＝∠CAD，∴∠FDA＝∠CAD，∴DF∥AC；（3）∵FD与BE不一定互相垂直，∴∠FDE＝90°不成立；（4）由（1）（2）得：∠EAD＝∠EDA，∠F AD＝∠CAD，又∵∠EDA＝∠B+∠F AD，∠EAD＝∠CAD+∠CAE，∴∠B＝∠CAE．故选：C．10．解：∵△ABC中，AD，BE分别为BC、AC边上的高，∴AD⊥BC，而△ABF和△ACF有一条公共边，∴S△ABF：S△AFC＝BD：CD，∴③正确；∵∠ABC＝45°，∴AD＝BD，∠DAC和∠FBD都是∠ACD的余角，而∠ADB＝∠ADC＝90°，∴△BDF≌△ADC，∴FD＝CD，∴∠FCD＝∠CFD＝45°，∴①正确；若AE＝EC，BE⊥AC，可得AB＝BC，与题意不符合，故②错误．若BF＝2EC，根据①得BF＝AC，∴AC＝2EC，即E为AC的中点，∴BE为线段AC的垂直平分线，∴AF＝CF，BA＝BC，∴AB＝BD+CD＝AD+CD＝AF+DF+CD＝CF+DF+CD，即△FDC周长等于AB的长，∴④正确．故选：D．11．解：∵AC的垂直平分线分别交BC、AC于点D、E，∴AD＝DC，∴△ABD的周长为AB+AD+BD＝AB+DC+BD＝AB+BC，∵C△ABD＝16cm，AB＝5cm，∴BC＝11cm，故选：D．12．解：设CE＝x，连接AE．∵DE是线段AB的垂直平分线，∴AE＝BE＝BC+CE＝3+x，∴在Rt△ACE中，AE2＝AC2+CE2，即（3+x）2＝42+x2，解得x＝．在Rt△ABC中，AB＝＝5，∴BD＝AD＝，在Rt△BDE中，DE＝＝，故选：B．13．解：∵三角形三边垂直平分线的交点到三个顶点的距离相等，∴猫应该蹲守在△ABC三边垂直平分线的交点处．故选：A．14．解：∵DE是线段AB的中垂线，GF是线段BC的中垂线，∴EB＝EA，GB＝GC，∵△BEG周长为16，∴EB+GB+EG＝16，∴EA+GC+EG＝16，∴GA+EG+EG+EG+EC＝16，∴AC+2EG＝16，∵EG＝1，∴AC＝14，故选：B．15．解：∵P A平分∠CAB，PB平分∠CBE，∴∠P AB＝∠CAB，∠PBE＝∠CBE，∵∠CBE＝∠CAB+∠ACB，∠PBE＝∠P AB+∠APB，∴∠ACB＝2∠APB；故①正确；过P作PM⊥AB于M，PN⊥AC于N，PS⊥BC于S，∴PM＝PN＝PS，∴PC平分∠BCD，∵S△P AC：S△P AB＝（AC•PN）：（AB•PM）＝AC：AB；故②正确；∵BE＝BC，BP平分∠CBE∴BP垂直平分CE（三线合一），故③正确；∵PG∥AD，∴∠FPC＝∠DCP∵PC平分∠DCB，∴∠DCP＝∠PCF，∴∠PCF＝∠CPF，故④正确．故选：D．16．解：连接AE，BE，过E作EG⊥BC于G，∵D是AB的中点，DE⊥AB，∴DE垂直平分AB，∴AE＝BE，∵∠ACE+∠BCE＝180°，∠ECG+∠BCE＝180°，∴∠ACE＝∠ECG，又∵EF⊥AC，EG⊥BC，∴EF＝EG，∠FEC＝∠GEC，∵CF⊥EF，CG⊥EG，∴CF＝CG，在Rt△AEF和Rt△BEG中，，∴Rt△AEF≌Rt△BEG（HL），∴AF＝BG，设CF＝CG＝x，则AF＝AC﹣CF＝12﹣x，BG＝BC+CG＝8+x，∴12﹣x＝8+x，解得x＝2，∴AF＝12﹣2＝10．故答案为：10．17．解：∵点D、E分别是AB、AC边的垂直平分线与BC的交点，∴AD＝BD，AE＝CE，∴∠B＝∠BAD，∠C＝∠CAE，∵∠B＝40°，∠C＝45°，∴∠B+∠C＝85°，∠BAC＝95°，∴∠BAD+∠CAE＝85°，∴∠DAE＝∠BAC﹣（∠BAD+∠CAE）＝95°﹣85°＝10°，故答案为：10°18．解：解法一：连接BO，并延长BO到P，∵线段AB、BC的垂直平分线l1、l2相交于点O，∴AO＝OB＝OC，∠BDO＝∠BEO＝90°，∴∠DOE+∠ABC＝180°，∵∠DOE+∠1＝180°，∴∠ABC＝∠1＝39°，∵OA＝OB＝OC，∴∠A＝∠ABO，∠OBC＝∠C，∵∠AOP＝∠A+∠ABO，∠COP＝∠C+∠OBC，∴∠AOC＝∠AOP+∠COP＝∠A+∠ABC+∠C＝2×39°＝78°；解法二：连接OB，∵线段AB、BC的垂直平分线l1、l2相交于点O，∴AO＝OB＝OC，∴∠AOD＝∠BOD，∠BOE＝∠COE，∵∠DOE+∠1＝180°，∠1＝39°，∴∠DOE＝141°，即∠BOD+∠BOE＝141°，∴∠AOD+∠COE＝141°，∴∠AOC＝360°﹣（∠BOD+∠BOE）﹣（∠AOD+∠COE）＝78°；故答案为：78°．19．解：∵AD是△ABC的角平分线，∠ACB＝90°，DE⊥AB，∴∠CAD＝∠EAD，DE＝CD，AE＝AC＝2，∵AD的垂直平分线交AB于点F，∴AF＝DF，∴∠ADF＝∠EAD，∴∠ADF＝∠CAD，∴AC∥DE，∴∠BDE＝∠C＝90°，∴△BDF、△BED是等腰直角三角形，设DE＝x，则EF＝BE＝x，BD＝DF＝2﹣x，在Rt△BED中，DE2+BE2＝BD2，∴x2+x2＝（2﹣x）2，解得x1＝﹣2﹣2（负值舍去），x2＝﹣2+2，∴△DEF的面积为（﹣2+2）×（﹣2+2）÷2＝6﹣4．故答案为：6﹣4．20．解：∵BD平分∠ABC，∴∠DBC＝∠ABD，∵∠A＝60°，∴∠ABC+∠ACB＝120°，∵∠ACF＝48°，∵BC的中垂线交BC于点E，∴BF＝CF，∴∠FCB＝∠FBC，∴∠ABC＝2∠FCE，∴3∠FCE＝120°﹣48°＝72°，∴∠FCE＝24°，∴∠ABC＝48°，故答案为：48°21．解：如图，过点D作DE⊥AB，交AB延长线于点E，DF⊥AC于F，∵AD是∠BOC的平分线，∴DE＝DF，∵DP是BC的垂直平分线，∴BD＝CD，在Rt△DEB和Rt△DFC中，，∴Rt△DEB≌Rt△DFC（HL）．∴∠BDE＝∠CDF，∴∠BDC＝∠EDF，∵∠DEB＝∠DFC＝90°，∴∠EAF+∠EDF＝180°，∵∠BAC＝85°，∴∠BDC＝∠EDF＝95°，故答案为：95°．22．解：∵DE是AB的垂直平分线，∴AF＝BF∴AC＝AF+CF＝BF+CF＝12+3＝15．23．解：（1）∵l1是AB边的垂直平分线∴DA＝DB，∵l2是AC边的垂直平分线，∴EA＝EC，BC＝BD+DE+EC＝DA+DE+EA＝6cm；（2）∵l1是AB边的垂直平分线，∴OA＝OB，∵l2是AC边的垂直平分线，∴OA＝OC，∵OB+OC+BC＝16cm，∴OA＝0B＝OC＝5cm；（3）∵∠BAC＝120°，∴∠ABC+∠ACB＝60°，∵DA＝DB，EA＝EC，∴∠BAD＝∠ABC，∠EAC＝∠ACB，∴∠DAE＝∠BAC﹣∠BAD﹣∠EAC＝60°．24．证明：∵∠ACB＝90°，DE⊥AB，∴∠ACB＝∠BDE＝90°，在Rt△BDE和Rt△BCE中，，∴Rt△BDE≌Rt△BCE，∴ED＝EC，∵ED＝EC，BD＝BC，∴BE垂直平分CD．25．证明：∵AD是∠BAC的平分线，∴∠1＝∠2，∵FE是AD的垂直平分线，∴F A＝FD（线段垂直平分线上的点到线段两端的距离相等），∴∠F AD＝∠FDA（等边对等角），∵∠BAF＝∠F AD+∠1，∠ACF＝∠FDA+∠2，∴∠BAF＝∠ACF．26．解：（1）∵点D是BC边的中点，DE⊥BC，∴PB＝PC，∴∠PBC＝∠PCB，∵BP平分∠ABC，∴∠PBC＝∠ABP，∴∠PBC＝∠PCB＝∠ABP，∵∠A＝60°，∠ACP＝24°，∴∠PBC+∠PCB+∠ABP＝120°﹣24°，∴3∠ABP＝120°﹣24°，∴∠ABP＝32°；（2）∵点D是BC边的中点，DE⊥BC，∴PB＝PC，∴∠PBC＝∠PCB，∵BP平分∠ABC，∴∠PBC＝∠ABP，∴∠PBC＝∠PCB＝∠ABP＝n°，∵∠A＝60°，∠ACP＝m°，∴∠PBC+∠PCB+∠ABP＝120°﹣m°，∴3∠ABP＝120°﹣m°，∴3n°+m°＝120°，故答案为：m+3n＝120．。

线段的垂直平分线与角平分线的性质【思维入门】1．如图1－3－1，在△ABC 中，∠ABC ＝50°， ∠ACB ＝60°，点E 在BC 的延长线上，∠ABC 的平分线BD 与∠ACE 的平分线CD 相交于点D ，连结AD .下列结论不正确的是( )A ．∠BAC ＝70°B ．∠DOC ＝90° C ．∠BDC ＝35°D ．∠DAC ＝55°2．如图1－3－2，BD 是∠ABC 的平分线，P 是BD 上的一点，PE ⊥BA 于点E ，PE ＝4 cm ，则点P 到边BC 的距离为____cm.图1－3－23．如图1－3－3，在Rt △ABC 中，∠A ＝90°，∠ABC 的平分线BD 交AC 于点D ，AD ＝5，BC ＝12，则△BDC 的面积是____．图1－3－34．如图1－3－4，在△ABC 中，DE ，FG 分别是△ABC 的边AB ，AC 的垂直平分线，若BC ＝10，则△ADF 的周长是多少？图1－3－45．已知，如图1－3－5所示，AB ＝AC ，BD ＝CD ，DE ⊥AB 于点E ，DF ⊥AC 于点F，求证：DE＝DF.【思维拓展】6．如图1－3－6，AD是△ABC中∠BAC的平分线，DE⊥AB于点E，S△ABC＝7，DE＝2，AB＝4，则AC的长是()5A．3 B．4C．6D．7．已知△ABC中，∠C＝90°，AD平分∠BAC交BC于D，若BC＝32，且BD∶CD＝9∶7，则D到AB的距离为()A．18 B．16 C．14 D．128．如图1－3－7，直线l1，l2，l3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则供选择的地址有()A．1处B．2处C．3处D．4处Array 9．如图1－3－8，在△ABC中，∠C＝90°，AB＝10，AD是△ABC的一条角平分线．若CD＝3，则△ABD的面积为____．。

自我小测
1、三角形的三边的垂直平分线的交点( )
A、必在三角形的内部
B、必在三角形的外部
C、必在三角形的一边上
D、以上都有可能
2、在△ABC内部有一点P，到△ABC的三个顶点的距离相等，即PA=PB=PC，则点P 一定是( )
A、三角形三条中线的交点
B、三角形三条高的交点
C、三角形三边垂直平分线的交点
D、三角形三个内角的平分线的交点
3、如图16–2–14所示，在△ABC中，BC=15，PQ，MN分别为AB，AC的垂直平分线，则△APM的周长为、
4、已知如图16–2–15所示，过点A作△ABC边BC上的高、(保留作图痕迹，不写作法)
图16–2–14 图16–2–15
参考答案
1、D 解析：由锐角三角形三边的垂直平分线的交点在三角形的内部，直角三角形三边的垂直平分线的交点在三角形的斜边上，钝角三角形三边的垂直平分线的交点在三角形的外部、
2、C 解析：到三个顶点距离相等的点是三角形三边垂直平分线的交点、
3、15 解析：由PQ垂直平分AB知，AP=BP、由MN垂直平分AC知，AM=CM、
∴△APM的周长为BC的长、
4、解：如图D–16–2所示、
AM为△ABC边BC上的高、
图D–16–2。

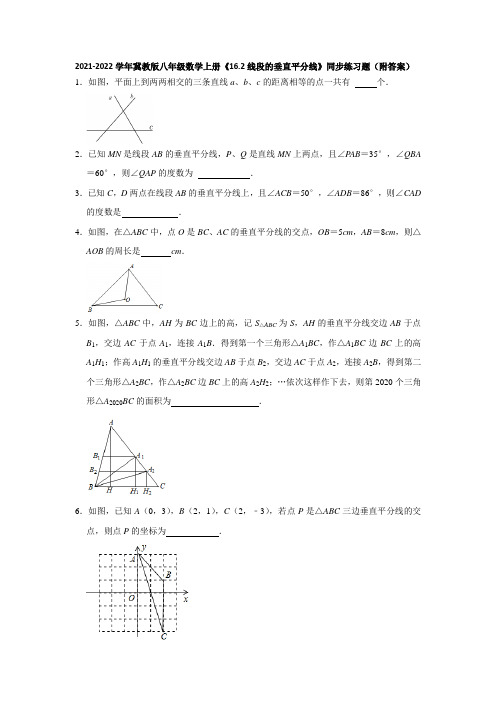
2021-2022学年冀教版八年级数学上册《16.2线段的垂直平分线》同步练习题（附答案）1．如图，平面上到两两相交的三条直线a、b、c的距离相等的点一共有个．2．已知MN是线段AB的垂直平分线，P、Q是直线MN上两点，且∠P AB＝35°，∠QBA ＝60°，则∠QAP的度数为．3．已知C，D两点在线段AB的垂直平分线上，且∠ACB＝50°，∠ADB＝86°，则∠CAD 的度数是．4．如图，在△ABC中，点O是BC、AC的垂直平分线的交点，OB＝5cm，AB＝8cm，则△AOB的周长是cm．5．如图，△ABC中，AH为BC边上的高，记S△ABC为S，AH的垂直平分线交边AB于点B1，交边AC于点A1，连接A1B．得到第一个三角形△A1BC，作△A1BC边BC上的高A1H1；作高A1H1的垂直平分线交边AB于点B2，交边AC于点A2，连接A2B，得到第二个三角形△A2BC，作△A2BC边BC上的高A2H2；…依次这样作下去，则第2020个三角形△A2020BC的面积为．6．如图，已知A（0，3），B（2，1），C（2，﹣3），若点P是△ABC三边垂直平分线的交点，则点P的坐标为．7．如图，在△ABC中，∠C＝90°，点E是AC上的点，且∠1＝∠2，DE垂直平分AB，垂足是D，S△AED：S△ABC＝．8．如图，将△ABC放在每个小正方形边长均为1的网格中，点A、B、C均落在格点上，若点B的坐标为（3，﹣1），点C的坐标为（2，2），则到△ABC三个顶点距离相等的点的坐标为．9．如图，在△ABC中，AB边的垂直平分线l1交BC于D，AC边的垂直平分线l2交BC于E，l1与l2相交于点O，△ADE的周长为8cm．（1）求BC的长；（2）分别连结OA、OB、OC，若△OBC的周长为18cm，求OA的长．10．在△ABC中，AB的垂直平分线分别交线段AB，BC于点M，P，AC的垂直平分线分别交线段AC，BC于点N，Q．（1）如图，当∠BAC＝80°时，求∠P AQ的度数；（2）当∠BAC满足什么条件时，AP⊥AQ，说明理由；（3）在（2）的条件下，BC＝10，求△APQ的周长．11．如图，在△ABC中，点E是BC边上的一点，连接AE，BD垂直平分AE，垂足为F，交AC于点D，连接DE．（1）若△ABC的周长为18，△DEC的周长为6，求AB的长．（2）若∠ABC＝30°，∠C＝45°，求∠CDE的度数．12．如图，在四边形ABCD中，BD所在的直线垂直平分线段AC，过点A作BC的平行线AF交CD于F，延长AB、DC交于点E．求证：（1）AC平分∠EAF；（2）∠F AD＝∠E．13．如图，在△ABC中，DM，EN分别垂直平分边AC和边BC，交边AB于M，N两点，DM与EN相交于点F．（1）若AB＝3cm，求△CMN的周长．（2）若∠MFN＝70°，求∠MCN的度数．14．如图，在△ABC中，AB边的垂直平分线l1交BC于点D，AC边的垂直平分线l2交BC 于点E，l1与l2相交于点O，连接OB，OC．若△ADE的周长为12cm，△OBC的周长为32cm．（1）求线段BC的长；（2）连接OA，求线段OA的长；（3）若∠BAC＝n°（n＞90），直接写出∠DAE的度数°．15．已知：△ABC是三边都不相等的三角形，点O和点P是这个三角形内部两点．（1）如图①，如果点P是这个三角形三个内角平分线的交点，那么∠BPC和∠BAC有怎样的数量关系？请说明理由；（2）如图②，如果点O是这个三角形三边垂直平分线的交点，那么∠BOC和∠BAC有怎样的数量关系？请说明理由；（3）如图③，如果点P（三角形三个内角平分线的交点），点O（三角形三边垂直平分线的交点）同时在不等边△ABC的内部，那么∠BPC和∠BOC有怎样的数量关系？请直接回答．16．已知：如图，AB＝AC，DB＝DC，点E在AD上，求证：EB＝EC．17．如图，AD与BC相交于点O，OA＝OC，∠A＝∠C，BE＝DE．求证：OE垂直平分BD．18．如图，在△ABC中，∠ABC＝45°，CD⊥AB于点D，AC的垂直平分线BE与CD交于点F，与AC交于点E．（1）判断△DBC的形状并证明你的结论．（2）求证：BF＝AC．（3）试说明CE＝BF．19．如图，OE，OF分别是AC，BD的垂直平分线，垂足分别为E，F，且AB＝CD，∠ABD ＝120°，∠CDB＝38°，求∠OBD的度数．20．如图，在△ABC中，∠ACB＝90°，∠A＝30°，AB的垂直平分线分别交AB和AC于点D，E．求证：DE＝EC．（用三种方法证明）21．如图，Rt△ABC中，∠ACB＝90°，D是AB上一点，BD＝BC，过点D作AB的垂线交AC于点E，求证：BE垂直平分CD．参考答案1．解：如图，到三条直线a、b、c的距离都相等的点一共有4个．故答案为：4．2．解：当点P、Q在AB的同旁时，∵MN是线段AB的垂直平分线，∴QA＝QB，∵∠QBA＝60°，∴∠QAB＝∠QBA＝60°，∴∠QAP＝∠QAB﹣∠P AB＝60°﹣35°＝25°，当点P、Q′在AB的两旁时，∴∠Q′AP＝∠Q′AB+∠P AB＝60°+35°＝95°，故答案为：25°或95°．3．解：∵C、D两点在线段AB的中垂线上，∴CA＝CB，DA＝DB，∵CD⊥AB，∴∠ACD＝∠ACB＝×50°＝25°，∠ADC＝∠ADB＝×86°＝43°，当点C与点D在线段AB两侧时，∠CAD＝180°﹣∠ACD﹣∠ADC＝180°﹣25°﹣43°＝112°，当点C与点D′在线段AB同侧时，∠CAD′＝∠AD′C﹣∠ACD′＝43°﹣25°＝18°，故答案为：18°或112°．4．解：∵点O是BC、AC的垂直平分线的交点，∴OA＝OB＝5cm，∴△AOB的周长＝OA+OB+AB＝18（cm），故答案为：18．5．解：如图所示，连接A1H，∵AH的垂直平分线交边AB于点B1，交边AC于点A1，∴AA1＝HA1，∴∠HAC＝∠AHA1，又∵AH⊥BC，∴∠HAC+∠C＝∠AHA1+∠CHA1＝90°，∴∠C＝∠CHA1，∴HA1＝CA1，∴AA1＝CA1，∴A1是AC的中点，∴△A1BC的面积＝S△ABC＝S，同理可得，A2是A1C的中点，∴△A2BC的面积＝S△A1BC＝S，同理可得，△A3BC的面积＝S△A2BC＝，……，∴第2020个三角形△A2020BC的面积为，故答案为：．6．解：如图所示：分别作线段AB、BC的垂直平分线交于点P，点P的坐标为（﹣2，﹣1），故答案为：（﹣2，﹣1）．7．解：∵DE垂直平分AB，∴AD＝BD，∴S△ADE＝S△BDE，∵∠1＝∠2，∠C＝∠BDE＝90°，BE＝BE，∴△BDE≌△BCE（AAS），∴S△BDE＝S△BCE，∴S△AED：S△ABC＝1：3，故答案为：1：3．8．解：∵点P到△ABC三个顶点距离相等，∴点P是边AB、AC的垂直平分线的交点，如图所示：点P即为所求，此时点P的坐标为（1，0），故答案为：（1，0）．9．解：（1）在△ABC中，AB边的垂直平分线l1交BC于D，AC边的垂直平分线l2交BC 于E，l1与l2相交于点O，∴AD＝BD，AE＝CE，∵△ADE的周长为8cm．∴BC＝BD+DE+CE＝AD+DE+AE＝8cm；（2）连接OA、OB、OC，在△ABC中，AB边的垂直平分线l1交BC于D，AC边的垂直平分线l2交BC于E，l1与l2相交于点O，∴OA＝OB，OA＝OC，∴OA＝OB＝OC，∵△OBC的周长为18cm，∴OB+OC+BC＝18cm，∴OB＝OC＝5cm，∴OA＝5cm．10．解：（1）∵MP、NQ分别是AB、AC的垂直平分线，∴AP＝BP，AQ＝CQ，∵∠BAC＝80°，∴∠B+∠C＝180°﹣80°＝100°，∵AP＝BP，AQ＝CQ，∴∠BAP＝∠B，∠CAQ＝∠C，∴∠P AQ＝∠BAC﹣∠BAP﹣∠CAQ＝∠BAC﹣∠B﹣∠C＝100°﹣80°＝20°；（2）如图，∵AP⊥AQ，∴∠P AQ＝90°，由（1）得，∠BAP＝∠B，∠CAQ＝∠C，∴∠B+∠C＝180°﹣∠BAC，∠BAP+∠CAQ＝∠BAC﹣90°，∴180°﹣∠BAC＝∠BAC﹣90°，∴∠BAC＝135°；答：当∠BAC＝135°时，AP⊥AQ；（3）∵△APQ周长＝AP+PQ+AQ＝BP+PQ+QC＝BC，∵BC＝10，∴△APQ周长＝10．11．解：（1）∵BD是线段AE的垂直平分线，∴AB＝BE，AD＝DE，∵△ABC的周长为18，△DEC的周长为6，∴AB+BE+EC+CD+AD＝18，CD+EC+DE＝CD+CE+AD＝6，∴AB+BE＝18﹣6＝12，∴AB＝6；（2）∵∠ABC＝30°，∠C＝45°，∴∠BAC＝180°﹣30°﹣45°＝105°，在△BAD和△BED中，，∴△BAD≌△BED（SSS），∴∠BED＝∠BAC＝105°，∴∠CDE＝∠BED﹣∠C＝105°﹣45°＝60°．12．证明：（1）∵BD所在的直线垂直平分线段AC，∴BA＝BC，∴∠BAC＝∠BCA，∵BC∥AF，∴∠CAF＝∠BCA，∴∠CAF＝∠BAC，即AC平分∠EAF；（2）∵BD所在的直线垂直平分线段AC，∴DA＝DC，∴∠DAC＝∠DCA，∵∠DCA是△ACE的一个外角，∴∠DCA＝∠E+∠EAC，∴∠E+∠EAC＝∠F AD+∠CAF，∵∠CAF＝∠EAC，∴∠F AD＝∠E．13．解：（1）∵DM、EN分别垂直平分AC和BC，∴AM＝CM，BN＝CN，∴△CMN的周长＝CM+MN+CN＝AM+MN+BN＝AB＝3（cm）；（2）∵∠MFN＝70°，∴∠MNF+∠NMF＝180°﹣70°＝110°，∵∠AMD＝∠NMF，∠BNE＝∠MNF，∴∠AMD+∠BNE＝∠MNF+∠NMF＝110°，∴∠A+∠B＝90°﹣∠AMD+90°﹣∠BNE＝180°﹣110°＝70°，∵AM＝CM，BN＝CN，∴∠A＝∠ACM，∠B＝∠BCN，∴∠MCN＝180°﹣2（∠A+∠B）＝180°﹣2×70°＝40°．14．解：（1）∵l1是AB边的垂直平分线，∴DA＝DB，∵l2是AC边的垂直平分线，∴EA＝EC，BC＝BD+DE+EC＝DA+DE+EA＝12cm；（2）∵l1是AB边的垂直平分线，∴OA＝OB，∵l2是AC边的垂直平分线，∴OA＝OC，∵OB+OC+BC＝32cm，∴OA＝OB＝OC＝10cm；（3）∵∠BAC＝n°，∴∠ABC+∠ACB＝（180﹣n）°，∵DA＝DB，EA＝EC，∴∠BAD＝∠ABC，∠EAC＝∠ACB，∴∠DAE＝∠BAC﹣∠BAD﹣∠EAC＝n°﹣（180°﹣n°）＝2n°﹣180°．故答案为：（2n﹣180）．15．解：（1）∠BPC＝90°+∠BAC∵BP平分∠ABC，CP平分∠ACB，∴∠PBC＝∠ABC，∠PCB＝∠ACB，∴∠BPC＝180°﹣（∠PBC+∠PCB）＝180°﹣（∠ABC+∠ACB）＝180°﹣（∠ABC+∠ACB）＝180°﹣（180°﹣∠BAC）＝90°+∠BAC；（2）∠BOC＝2∠BAC如图，连接AO．∵点O是这个三角形三边垂直平分线的交点，∴OA＝OB＝OC，∴∠OAB＝∠OBA，∠OAC＝∠OCA，∠OBC＝∠OCB，∴∠AOB＝180°﹣2∠OAB，∠AOC＝180°﹣2∠OAC，∴∠BOC＝360°﹣（∠AOB+∠AOC）＝360°﹣（180°﹣2∠OAB+180°﹣2∠OAC），＝2∠OAB+2∠OAC＝2∠BAC；（3）4∠BPC﹣∠BOC＝360°，∵点P为三角形三个内角平分线的交点，∴∠BPC＝90°+∠BAC由∠BAC＝2∠BPC﹣180°点O为三角形三边垂直平分线的交点∠BOC＝2∠BAC，∴∠BOC＝2（2∠BPC﹣180°）＝4∠BPC﹣360°，即4∠BPC﹣∠BOC＝360°．16．解：∵AB＝AC，DB＝DC，∴AD是线段BC的垂直平分线，∵点E在AD上，∴EB＝EC．17．证明：在△AOB与△COD中，，∴△AOB≌△COD（ASA），∴OB＝OD，∴点O在线段BD的垂直平分线上，∵BE＝DE，∴点E在线段BD的垂直平分线上，∴OE垂直平分BD．18．解：（1）△DBC是等腰直角三角形，理由：∵∠ABC＝45°，CD⊥AB，∴∠BCD＝45°，∴BD＝CD，∴△DBC是等腰直角三角形；（2）∵BE⊥AC，∴∠BDC＝∠BEC＝90°，∵∠BFD＝∠CFE，∴∠DBF＝∠ACD，在△BDF与△CDA中，，∴△BDF≌△CDA，∴BF＝AC；（3）∵BE是AC的垂直平分线，∴CE＝AC，∴CE＝BF．19．解：连接OA，OC，∵OE，OF分别是AC，BD的垂直平分线，∴OA＝OC，OB＝OD，∵AB＝CD，∴△ABO≌△CDO（SSS），∴∠ABO＝∠CDO，设∠OBD＝∠ODB＝α，∠ABO＝∠CDO＝β，∴α+β＝120°，β﹣α＝38°，∴α＝41°，∴∠OBD＝41°．20．证明：方法一：如图1，连接BE，∵DE是AB的垂直平分线，∴BE＝AE，∠ABE＝∠A＝30°，∵∠ACB＝90°，∠A＝30°，∴∠ABC＝60°，∴∠CBE＝∠DBE＝30°，∵DE⊥AB，CE⊥BC，∴CE＝DE；方法二：如图2，连接CD，∵在△ABC中，∠ACB＝90°，∠A＝30°，∴∠B＝60°，∵点D是AB的中点，∴CD＝BD＝AB，∴△BDC是等边三角形，∴∠BCD＝∠BDC＝60°，∵∠BDE＝∠ACB＝90°，∴∠EDC＝∠ECD＝30°，∴DE＝CE；方法三：如图3，延长DE交BC的延长线于F，∵∠ACB＝90°，∠A＝30°，∴∠B＝60°，BC＝AB，∵DE垂直平分AB，∴BD＝AD＝AB，∠BDF＝90°，∴∠F＝30°，∴BD＝BF，∴CF＝BD＝AD，在△ADE与△FCE中，∴△ADE≌△FCE（AAS），∴DE＝CE．21．证明：∵∠ACB＝90°，DE⊥AB，∴∠ACB＝∠BDE＝90°，在Rt△BDE和Rt△BCE中，，∴Rt△BDE≌Rt△BCE，∴ED＝EC，∵ED＝EC，BD＝BC，∴BE垂直平分CD．。

自我小测
1．三角形的三边的垂直平分线的交点( )
A．必在三角形的内部B．必在三角形的外部
C．必在三角形的一边上D．以上都有可能
2．在△ABC内部有一点P，到△ABC的三个顶点的距离相等，即PA=PB=PC，则点P 一定是( )
A．三角形三条中线的交点B．三角形三条高的交点
C．三角形三边垂直平分线的交点D．三角形三个内角的平分线的交点
3．如图16–2–14所示，在△ABC中，BC=15，PQ，MN分别为AB，AC的垂直平分线，则△APM的周长为．
4．已知如图16–2–15所示，过点A作△ABC边BC上的高．(保留作图痕迹，不写作法)
图16–2–14 图16–2–15
参考答案
1．D 解析：由锐角三角形三边的垂直平分线的交点在三角形的内部，直角三角形三边的垂直平分线的交点在三角形的斜边上，钝角三角形三边的垂直平分线的交点在三角形的外部．
2．C 解析：到三个顶点距离相等的点是三角形三边垂直平分线的交点．
3．15 解析：由PQ垂直平分AB知，AP=BP．由MN垂直平分AC知，AM=CM．∴△APM的周长为BC的长．
4．解：如图D–16–2所示．
AM为△ABC边BC上的高．
图D–16–2。

八年级数学上册线段的垂直平分线的性质练习一、单选题1．到三角形的三个顶点距离相等的点是（ ）． A ．三角形三条中线的交点B ．三角形三边垂直平分线的交点C ．三角形三条角平分线的交点D ．三角形三条高的交点2．如图，DE 为ABC 中AC 边的中垂线，8,10BC AB ==，则EBC 的周长是（ ）A ．16B ．18C ．26D ．283．下列条件中，不能判定直线CD 是线段AB (C ，D 不在线段AB 上)的垂直平分线的是（ ） A ．CA =CB ，DA =DBB ．CA =CB ，CD ⊥ABC ．CA =DA ，CB =DBD ．CA =CB ，CD 平分AB4．如图，直线PO 与AB 交于点O ，PA PB =，下列结论中正确的是（ ）A ．AO BO =B ．PO AB ⊥C ．PO 是AB 的垂直平分线D ．点P 在AB 的垂直平分线上5．如图，AD BE ⊥，BD DE =，点E 在线段AC 的垂直平分线上，若6cm AB =，3cm BD =，则DC 的长为（ ）A ．3cmB ．6cmC ．9cmD ．12cm6．如图，有A 、B 、C 三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在（ ）．A ．在 AC 、BC 两边高线的交点处B ．在 AC 、BC 两边垂直平分线的交点处 C ．在 AC 、BC 两边中线的交点处D ．在∠A 、∠B 两内角平分线的交点处二、填空题 7．如图，在ABC 中，10AB =，AD 垂直平分线段BC ，垂足为点D ，点E 是AC 的中点，则EC 的长为________．8．如图，在ABC 中，90,ACB DE ∠=︒是AB 的垂直平分线，:4:1CAE EAB ∠∠=，则B 的度数为_______．9．如图，撑伞时，把伞“两侧的伞骨”和支架分别看作AB 、AC 和DB 、DC ，始终有,AB AC DB DC ==，请大家考虑一下伞杆AD 与B 、C 的连线BC 的位置关系为________．10．已知线段AB 及一点P ，PA=PB=3cm ，则点P 在__________上．11．如图，△ABC 中，DE 是AC 的垂直平分线，AE=5cm ，△ABD 的周长为14cm ，则△ABC 的周长为________cm ．12．如图，△ABC 中，∠C ＝90°，DE 是AB 的垂直平分线，且BC ＝8，AC ＝6，则△ACD 的周长为_____．三、解答题13．如图，求作一点P ，使PC PD =，并且点P 到AOB ∠两边的距离相等．14．如图，A ，B 表示两个仓库，要在A ，B 一侧的河岸边建造一个码头，使它到两个仓库的距离相等，码头应建造在什么位置？15．已知：如图，AB 是线段CD 的垂直平分线，E ，F 是AB 上的两点．求证：ECF EDF ∠=∠．16．如图，甲､乙两个单位分别位于一条封闭式街道的两旁，现准备合作修建一座过街天桥．（1）天桥建在何处才能使由甲到乙的路线最短？注意：天桥必须与街道垂直． （2）天桥建在何处才能使甲､乙到天桥的距离相等？17．已知：如图，P 是AOB ∠平分线上的一点，,⊥⊥PC OA PD OB ，垂足分别为C ，D ． 求证：（1）OC OD =；（2）OP 是CD 的垂直平分线．18．如图，小河边有两个村庄A 、B ．要在河边建一自来水厂向A 村与B 村供水． （1）若要使水厂到A 、B 村的距离相等，则应选择在哪建厂？（2）若要使水厂到A 、B 村的水管最省料，应建在什么地方？（保留作图痕迹，不写作法）参考答案1．B 【解析】解： 线段的垂直平分线上的点到线段的两个端点的距离相等， ∴ 到三角形的三个顶点距离相等的点是三角形三边的垂直平分线的交点. 故选：B2．B【解析】∵DE 是ABC ∆中AC 边的垂直平分线，∴AE CE =，∴10AE BE CE BE +=+=，∴EBC ∆的周长81018BE CE BC =++=+=．故选：B ．3．C【解析】解：A 、CA =CB ，DA =DB ，可以判定直线CD 是线段AB (C ，D 不在线段AB 上)的垂直平分线，不符合题意；B 、CA =CB ，CD ⊥AB ，可以判定直线CD 是线段AB (C ，D 不在线段AB 上)的垂直平分线，不符合题意；C 、CA =DA ，CB =DB ，不能判定直线CD 是线段AB (C ，D 不在线段AB 上)的垂直平分线，符合题意；D 、CA =CB ，CD 平分AB ，可以判定直线CD 是线段AB (C ，D 不在线段AB 上)的垂直平分线，不符合题意．故选：C ．4．D【解析】解：因为直线PO 与AB 交于点O ，且P A =PB ，所以P 在线段AB 的垂直平分线上，故选：D ．5．C【解析】解：AD BE ⊥，BD DE =，6AE AB ∴==，点E 在线段AC 的垂直平分线上，EA EC ∴=，9()DC DE EC AB BD cm ∴=+=+=，故选：C ．6．B【解析】解：根据线段垂直平分线上的点到线段两个端点的距离相等， 可知超市应建在AC 、BC 两边垂直平分线的交点处，故选：B ．7．5【解析】∵AD 垂直平分BC ，10AB =，∴10AC AB ==，∵点E 是AC 的中点， ∴152EC AC ==． 故答案为：5．8．15°【解析】解：∵在Rt △ABC 中，90ACB ∠=︒，∵DE 是AB 的垂直平分线∴∠B =∠BAE∵∠CAE ：∠EAB =4：1∴6∠B =90°∴∠B =15°故答案为:15°．9．垂直【解析】解：如图，连接BC 、AD ，∵,AB AC DB DC ==，∴点A 在线段BC 的垂直平分线上，点D 在线段BC 的垂直平分线上， ∴根据两点确定一条直线得出直线AD 是线段BC 的垂直平分线，故答案为：垂直．10．线段AB的垂直平分线【解析】因为PA=PB=3cm，所以P点一定在线段AB的垂直平分线上．故答案为：线段AB的垂直平分线．11．24【解析】∵DE是AC的垂直平分线∴AD=CD,AE=EC=5cm,∴AC=10cm∵△ABD的周长为14cm∴AB+BD+AD=14，△ABC的周长为AB+BC+AC= AB+ BD+ CD+AC= AB+BD+AD+AC=14+10=24cm. 12．14．【解析】∵DE是AB的垂直平分线，∴DA＝DB，∴△ACD的周长＝AC+CD+AD＝AC+CD+DB ＝AC+BC＝14．故答案为14．13．图见解析【解析】解：如下图所示，点P就是所求的点．14．见解析．【解析】解：连接AB，分别以A和B为圆心，以大于1AB为半径的两弧交于点E和F，2作直线EF，与河岸交于点C，如图，则码头应建在点C处．15．证明见解析 【解析】证明：AB 是线段CD 的垂直平分线，E ，F 是AB 上的两点， ∴,EC ED FC FD ==，又EF EF =，∴EDF ECF △≌△（SSS ），∴ECF EDF ∠=∠．16．（1）见解析；（2）见解析 【解析】解：（1）如图（1），将点A 沿竖直向下的方向平移，平移距离等于桥长，到达点1A ，连接1A B ，与街道靠近B 的一侧交于点1B ，过1B 点建桥即符合要求； （2）如图（2），作点B 关于街道的对称点2B ，连接2AB ，作2AB 的垂直平分线，与街道靠近A 的一侧相交于点2A ，过2A 点建桥即符合要求．17．（1）证明见解析；（2）证明见解析． 【解析】解：（1）证明：∵P 是∠AOB 平分线上的一点，PC ⊥OA ，PD ⊥OB ， ∴PC =PD ，在Rt △POC 与Rt △POD 中，∵PC PD OP OP =⎧⎨=⎩，∴Rt △POC ≌Rt △POD （HL ）， ∴OC =OD ；（2）证明：∵P 是∠AOB 平分线上的一点，∴∠COP =∠DOP∵由（1）知，OC =OD ，∴在△COE 与△DOE 中，OC OD COP DOP OE OE =⎧⎪∠=∠⎨⎪=⎩， ∴△COE ≌△DOE ，∴CE =DE ，OE ⊥CD ，即OP 是CD 的垂直平分线．18．（1）答案见解析；（2）答案见解析． 【解析】解：（1）作出AB 的中垂线与EF 的交点M ，交点M 即为厂址所在位置；（2）如图所示：作A 点关于直线EF 的对称点A′，再连接A′B 交EF 于点N ，点N 即为所求．。

冀教版八年级数学上册《16.2线段的垂直平分线》同步测试题带答案学校:___________班级：___________姓名：___________考号：___________一、选择题1．A、B、C三名选手站在一个三角形的三个顶点的位置上，他们在玩抢凳子游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的最适当的位置是在△ABC的（）A．三边中线的交点B．三边垂直平分线的交点C．三条角平分线的交点D．三边上高的交点2．如图，在Rt△ABC中∠C=90°，分别以点A，B为圆心，大于12AB长为半径画弧，两弧分别相交于AB两侧的M，N两点，直线MN交AB于点D，交AC于点E，若∠B=55°，则∠CBE=（）A．15°B．20°C．35°D．55°3．如图，DE是△ABC中AC边的垂直平分线，若BC=6厘米，AB=10厘米，则△EBC的周长为（）A．14厘米B．16厘米C．24厘米D．26厘米4．图，在ΔABC中AC=5，线段AB的垂直平分线交AC于点D,ΔBCD的周长是9，则BC的长为（）A．3B．4C．5D．65．如图，在四边形ABCD中AB∥DC，E为BC的中点，连接DE、AE，AE⊥DE，延长DE交AB的延长线于点F．若AB=5，CD=3，则AD的长为（）A．2B．5C．8D．116．如图，在△ABC中∠B=70°,∠C=34°，分别以点A和点C为圆心，大于12AC的长为半径画弧，两弧相交AC的两侧于点M，N，作直线MN，交BC于点D，连接AD，则∠BAD的度数为（）A．52°B．42°C．32°D．22°7．如图所示，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在（）A．在AC、BC两边高线的交点处B．在AC、BC两边中线的交点处C．在AC、BC两边垂直平分线的交点处D．在∠A、∠B两内角平分线的交点处8．如图，在△ABC中∠BAC=90°，AB=3，AC=4，BC=5，EF垂直平分BC，点P为直线EF上的任一点，则AP+BP的最小值是（）A．3B．4C．5D．69．两组邻边分别相等的四边形叫做“筝形”．如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB 小明在探究筝形的性质时，连结了AC，BD，并设交点为O，得到了如下结论，其中错误的是（）A．AC⊥BD B．AO=CO=12ACC．△ABD≌△CBD D．AO+DO=BO10．如图，在△ABC中，AB的垂直平分线分别交AB，BC于点D，E，AC的垂直平分线分别交AC，BC于点F，G，且△AEG的周长是20，则线段BC的长为（）A．40B．20C．15D．1011．如图，在△ABC中，AB＝AC，△A＝36°，分别以A和B为圆心，大于12AB的长为半径作弧，两弧相交于M，N两点，作直线MN分别交AB、AC于点F、D，作DE△BC于E．有下面三个结论：①BD平分△ABC；②DE＝DF；③BC+CD＝2AF；其中，正确的结论的个数是（）A．3B．2C．1D．0二、填空题12．如图，已知AB平分∠CAD，AC=AD，E在AB上，结论：①BC=BD；②CE=DE；③BA平分∠CBD；④AB所在的直线是CD的垂直平分线．其中正确的是（填序号）13．如图，在△ABC中∠A=90°，点D为AB上一点，将△ABC沿CD所在直线折叠，点A恰好落在BC边上的点E处，且CE=BE，则∠B的度数为．14．如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，若BC=9，AC=7，则△ACE的周长为．15．如图，在四边形ABCD中，AB//DC，E为BC的中点，连接DE、AE，AE△DE，延长DE交AB 的延长线于点F．若AB＝5，CD＝3，则AD的长为．16．如图，在△ABC中∠A=80°，点D是BC上一点，BD，CD的垂直平分线分别交AB，AC于点E，F，则∠EDF=度．17．如图，直线l垂直平分△ABC的AB边，在直线l上任取一动点O，连结OA、OB、OC．若OA=5，则OB=．若AC=9，BC=6，则△BOC的最小周长是．三、解答题18．如图，△ABC中AD⊥BC，EF垂直平分AC，交AC于点F，交BC于点E，且BD=DE．（1）若∠BAE=40°，求∠C的度数：（2）若△ABC周长13cm，AC=6cm，求DC长．19．如图，在△ABC中∠C=90°，分别以A、B为圆心，大于12AB长为半径画弧，两弧相交于点M、N，作直线MN与AB交于点D，与BC交于点E，连接AE．（1）由作图可知：直线MN是线段AB的______；（2）当∠B=35°，求∠CAE的大小；（3）当AC=3，BC=4时，求△ACE的周长．参考答案1．B2．B3．B4．B5．C6．B7．C8．B9．D10．B11．A12．①②③④13．30°14．1615．816．8017．5；15 18．（1）35°（2）3.5cm 19．（1）垂直平分线（2）∠CAE=20°（3）△ACE的周长为7。

最新精选冀教版数学八年级上册16.2 线段的垂直平分课后辅导练习第六十一篇第1题【单选题】下列说法错误的是( )A、若E、D是线段AB的垂直平分线上的两点，则AD=BD，AE=BEB、若AD=BD，AE=BE，D、E是不同的两点，则直线DE是线段AB的垂直平分线C、若PA=PB，则点P在线段AB的垂直平分线上D、若PA=PB，则过点P的直线是线段AB的垂直平分线【答案】：【解析】：第2题【单选题】如图，在△ABC 中，∠BAC=90°，∠ABC=2∠C，BE 平分∠ABC 交AC 于E，AD⊥BE 于D，下列结论：①AC﹣BE=AE；②点 E 在线段BC 的垂直平分线上；③∠DAE=∠C；④BC=4AD，其中正确的个数有( )A、1 个B、2 个C、3 个D、4 个【答案】：【解析】：第3题【单选题】已知等腰三角形的底边长为a，底边上的高为h，用直尺和圆规作这个等腰三角形时，甲同学的作法是：先作底边BC=a，再作BC的垂直平分线MN交BC于点D，并在DM上截取DA=h，最后连结AB、AC，则△ABC即为所求作的等腰三角形；乙同学的作法是：先作高AD=h，再过点D作AD的垂线MN，并在MN上截取BC=a，最后连结AB、AC，则△ABC即为所求作的等腰三角形．对于甲乙两同学的作法，下列判断正确的是( )A、甲正确，乙错误B、甲错误，乙正确C、甲、乙均正确D、甲、乙均错误【答案】：【解析】：第4题【单选题】如图所示，已知AB是∠CAD的平分线，AC=AD，点E在线段AB上，下列结论：①BC=BD；②CE=DE；③BA平分∠CBD；④AB是CD的垂直平分线．其中正确的是( )A、①②④B、②③④C、①③④D、①②③④【答案】：【解析】：第5题【单选题】如图，AD是角平分线，E是AB上一点，AE=AC，EF∥BC交AC于F．下列结论①△ADC≌△ADE；②EC平分∠DEF；③AD垂直平分CE．其中结论正确的有( )个A、1B、2C、3D、0【答案】：【解析】：第6题【单选题】如图，将30°的直角三角尺ABC绕直角顶点A逆时针旋转到ADE的位置，使B点的对应点D落在BC 边上，连接EB，EC，则下列结论：①∠DAC=∠DCA；②ED为AC的垂直平分线；③∠BED=30°；④ED=2AB．其中正确的是( )A、①②③B、①②④C、②③④D、①②③④【答案】：【解析】：第7题【填空题】如图所示，已知线段AB=6，现按照以下步骤作图：①分别以点A，B为圆心，以大于有误AB的长为半径画弧，两弧相交于点C和点D；②连结CD交AB于点P．则线段PB的长为______．【答案】：【解析】：第8题【填空题】如图，AB＝AC＝8cm，DB＝DC，若∠ABC＝60°，则BE＝______cm.【答案】：【解析】：第9题【填空题】在矩形ABCD中，点P在AD上，AB=有误，AP=1．将直角尺的顶点放在P处，直角尺的两边分别交AB、BC于点E、F，连接EF（如图1）．当点E与点B重合时，点F恰好与点C重合（如图2）.将直角尺从图2中的位置开始，绕点P顺时针旋转，当点E和点A重合时停止．在这个过程中，从开始到停止，线段EF的中点所经过的路径长为．【答案】：【解析】：半径等于12的圆中，垂直平分半径的弦长为______．【答案】：【解析】：第11题【解答题】如图，在△ABC中，PM，PN分别为边AB，AC的垂直平分线，且它们交于点P，求证：点P也在边BC的垂直平分线上．【答案】：【解析】：如图,PA,PB分别切☉O于A,B,连结PO,AB,相交于点D,C是☉O上一点,∠C=60°.求∠APB的大小;若PO=20 cm,求△AOB的面积.【答案】：【解析】：第13题【综合题】如图，AB、AC分别是⊙O的直径和弦，OD⊥AC于点D，过点A作⊙O的切线与OD的延长线交于点P，PC、AB的延长线交于点F.求证：PC是⊙O的切线；若∠ABC=600,AB=10,求线段CF的长，【答案】：【解析】：第14题【综合题】如图（1）将长方形纸片ABCD的一边CD沿着CQ向下折叠，使点D落在边AB上的点P处．试判断线段CQ与PD的关系，并说明理由；如图（2），若AB=CD=5，AD=BC=3．求AQ的长；如图（2），BC=3，取CQ的中点M，连接MD，PM，若MD⊥PM，求AQ（AB+BC）的值．【答案】：【解析】：第15题【综合题】已知如图，以Rt△ABC的AC边为直径作⊙O交斜边AB于点E，连接EO并延长交BC的延长线于点D，点F为BC的中点，连接EF．求证：EF是⊙O的切线；若⊙O的半径为3，∠EAC=60°，求AD的长．【答案】：【解析】：。