【推荐】华东师大初中数学八年级上册勾股定理(提高)巩固练习.doc

B CA 14.2 勾股定理的应用课内训练1．如图，某人欲横渡一条河，由于水流的影响，实际上岸地点C 偏离了欲到达点B240m ，已知他在水中游了510m ，求该河宽度．2．在一棵树10m 高的B 处，有两只猴子，一只爬下树走到离树20m 处的池塘A 处；•另外一只爬到树顶D 处后直接跃到A 外，距离以直线计算，如果两只猴子所经过的距离相等，试问这棵树有多高？3．如图，正方形网格中，每个小正方形的边长为1，则网格上的三角形ABC中，边长为无理数的边数是（ ） A ．0 B ．1 C ．2 D ．345．如图，已知△ABC 中，AB=10，BC=9，AC=17，求BC 边上的高．B CA课外演练1．如图，一电线杆AB 的高为10米，当太阳光线与地面的夹角为60°时，其影长AC1.732，结果保留三个有效数字）（ ） A ．5.00米 B ．8.66米 C ．17.3米 D ．5.77米2．如图，一架25分米的梯子，斜立在一竖直的墙上，•这时梯的底部距墙底端7分米，如果梯子的顶端沿墙_A_C_B下滑4分米，那么梯的底部将平滑（ ）A ．9分米B ．15分米C ．5分米D ．8分米 3．一轮船以16海里/时的速度从A 港向东北方向航行，另一艘船同时以12海里/时的速度从A 港向西北方向航行，经过1.5小时后，它们相距________海里． 4．小明想知道学校旗杆的高，他发现旗杆上的绳子垂到地面还多1m ，当他把绳子的下端拉开5m•后，••发现下端刚好接触地面，你能帮助他把旗杆的高度求出来是__________．5．如图，铁路上A 、B 两点相距为25km ，C 、D 为两村庄，DA ⊥AB 于A ，CB•⊥AB 于B ，已知DA=15km ，CB=10km ，现在要在铁路AB 上建一个货运站E ，使得C 、D 两村到E•站距离相等，问E 站应建在离A 多少千米处？BCAED6．如图，△ABC 中，CD ⊥AB 于D ，若AD=2BD ，AC=6，BC=3，则BD 的长为（ ）A ．3B ．12C ．1D ．4 7．等腰三角形底边上的高为8，周长为32，则该等腰三角形面积为_______．8．如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫格点，以格点为顶点分别按下列要求画三角形： （1）使三角形的三边长分别为3； （2）使三角形为钝角三角形且面积为4（在图乙中画一个即可）．甲乙9．（1）四年一度的国际数学家大会于2002年8月20日在北京召开．•大会会标如图甲，它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形．•若大正方形的面积为13，每个直角三角形两直角边的和是5，求中间小正方形的面积；C AD （2）现有一张长为6.5cm ，宽为2cm 的纸片，如图乙，请你将它分割成6块，再拼合成一个正方形．乙10．如图，某公园内有一棵大树，为测量树高，•小明在C 处用测角仪测得树顶端A 的仰角为30°，已知测角仪高DC=1.4m ，BC=30m ，请帮助小明计算出树高AB取1.732，结果保留三个有效数字）．答案: 课内训练1．450米 2．15米3．C 点拨：5,BC ==． 4．作出两直角边长分别为2和35．8 点拨：过A 作BC 边上的高AD ，不妨设BD=x ，列方程102-x 2=172-（9+x ）2． 课外演练1．D 点拨：BC=2AC ，有AC 2+102=4AC 2，5.77．2．D分米，平滑后高为24-4=20（分米），即平滑15-7=8 （分米）．3．30 点拨：根据题意画出方位图，运用勾股定理解． 4．12米5．解：在直角三角形ADE 中，由勾股定理，得DE 2=AD 2+AE 2．_B _C_D_A在直角三角形BEC中，•由勾股定理，得EC2=BE2+BC2．因为DE=EC，因此DE2=EC2，所以AD2+AE2=BE2+BC2．所以152+AE2=（25-AE）2+102，解得AE=10（km）．6．A 点拨：设BD为x，则36-（2x）2=9-x2，x=3．7．48 点拨：设底边长为2x，则腰长为16-x，有（16-x）2=82+x2，x=6，∴S=12×2x×8=48．8．图略9．解：（1）设较长直角边为b，较短直角边为a，则小正方形的边长为：a-b．• 而斜边即为大正方形边长，且其平方为13，即a2+b2=13①，由a+b=5，两边平方，得a2+b2+2ab=25．•将①代入，得2ab=12．所以（b-a）2=b2+a2-2ab=13-12=1．即小正方形面积为1；（2）由（2）题中矩形面积为6.5×2=13与（1）题正方形面积相等，仿照甲图可得，算出其中a=2，b=3，如图．10．解：过点D作DE⊥AB于点E，则ED=BC=30m，EB=DC=1．4m．设AE=x米，在Rt△ADE中，∠ADE=30°，则AD=2x．由勾股定理，得AE2+ED2=AD2，即x2+302=（2x）2，解得x≈17.32．∴AB=AE+EB=17.32+1.4≈18.7（m）．答：树高AB约为18．7m．点拨：构造直角三角形，利用30°角所对的直角边等于斜边的一半和勾股定理建立方程．在利用勾股定理进行计算时，无直角三角形的情况下，•可适当添加垂线构造直角三角形，并利用勾股定理．。

2022-2023学年度华东师大版八年级数学上册课堂提升训练第14章勾股定理14.2 勾股定理的应用知识点勾股定理及其逆定理的应用1.(2022四川巴中平昌期末)如图,某超市为了吸引顾客,在超市门口离地高4.5 m的墙上,装有一个由传感器控制的门铃A,如图①所示,人只要移至距该门铃5 m及5 m以内的范围时,门铃就会自动发出语音“欢迎光临”.如图②所示,一个身高1.5 m的学生走到D处,门铃恰好自动响起,CE为该学生头顶所在的水平线,则BD的长为( )图①图②A.3 mB.4 mC.5 mD.7 m2.(2022吉林长春朝阳期末)如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9 cm,内壁高12 cm.若这支铅笔长为18 cm,则这只铅笔在笔筒外面部分的长度不可能是( )A.3 cmB.5 cmC.6 cmD.8 cm3.(2022江苏苏州铜罗中学月考)如图,两树高分别为10米和4米,相距8米,一只鸟从一树的树梢A飞到另一树的树梢C,则小鸟至少飞行米.4.(教材P128变式题)《九章算术》记载:“今有竹高一丈,末折抵地,去根四尺,问折者高几何?”译文:有一根直立的竹子高1丈(1丈=10尺),竹子从某处折断,竹梢触地面离竹子底部4尺处,如图,则竹子折断处离地面尺.5.(2022江西吉安期中)如图,台阶每一级高20 cm,宽40 cm,长90 cm.一只蚂蚁从A点爬到B点,最短路程是cm.6.(2022广东揭阳揭东月考)一艘轮船以16 km/h的速度离开港口向东北方向航行,另一艘轮船同时离开港口以30 km/h的速度向东南方向航行,它们离开港口半小时后相距km.7.(2022山东济南济阳期末)如图,小刚想知道学校旗杆的高度,他发现旗杆顶端A处的绳子垂到地面B处后还多2米.当他把绳子拉直并使下端刚好接触到地面C处时,发现绳子下端到旗杆下端的距离为6米,请你帮小刚求出旗杆的高度AB长.8.某运动会本着环保、舒适、温馨的出发点,对运动员休息区进行了精心设计.如图,四边形ABCD为休闲区域,四周是步道,中间是花卉种植区域,为减少拥堵,中间穿插了氢能源环保电动步道AC.经测量AB=9,BC=12,CD=8,AD=17.(1)求氢能源环保电动步道AC的长;(2)证明:AC⊥CD.9.(2022四川成都向阳桥中学月考)一架云梯长25 m,按如图所示的方式斜靠在一面墙上,梯子底端C离墙7 m.(1)这个梯子的顶端A距地面有多高?(2)如果梯子的顶端下滑了4 m,那么梯子的底部在水平方向滑动了多少米?能力提升全练10.(2021湖北襄阳中考,9,)我国古代数学著作《九章算术》中记载了一个问题:“今有池方一丈,葭(jiā)生其中央,出水一尺.引葭赴岸,适与岸齐.问水深几何?”(丈、尺是长度单位,1丈=10尺)其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度是多少?则水深为( )A.10尺B.11尺C.12尺D.13尺11.(2021湖南岳阳中考,15,)《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺8寸,门对角线的长恰好为1丈.问门高、宽各是多少?(1丈=10尺,1尺=10寸)如图,设门高AB为x尺,根据题意,可列方程为.12.(2019江苏南京中考,12,)无盖圆柱形杯子的展开图如图所示.将一根长为20 cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有cm.13.(2022吉林长春德惠期末,22,)《城市交通管理条例》规定:小汽车在城市街路上的行驶速度不得超过70千米/时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到车速检测仪A正前方30米的C处,过了2秒后,小汽车行驶至B处,若小汽车与观测点间的距离AB为50米,则这辆小汽车是否超速?请通过计算说明.素养探究全练14.[数学运算]台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力,如图,有一台风中心沿东西方向AB由A行驶向B,已知点C为一海港,且点C与直线AB 上的两点A,B的距离分别为AC=300 km,BC=400 km,又AB=500 km,以台风中心为圆心周围250 km以内为受影响区域.(1)求∠ACB的度数;(2)海港C受台风影响吗?为什么?(3)若台风的速度为20千米/小时,当台风运动到点E处时,海港C刚好受到影响,当台风运动到点F时,海港C刚好不受影响,即CE=CF=250 km,则台风影响该海港持续的时间有多长?答案全解全析基础过关全练1.B 由题意可知,BE=CD=1.5 m,AE=AB-BE=4.5-1.5=3 m,AC=5 m, 由勾股定理得BD=CE=√52-32=4(m),故选B.2.D 如图,根据题意可得AB=12 cm,BC=9 cm,△ABC是直角三角形,在Rt△ABC中,AC=√AB2+BC2=√122+92=15(m),所以18-15=3(cm),18-12=6(cm).则这只铅笔在笔筒外面部分的长度在3 cm～6 cm之间.观察选项,只有选项D中长度不可能,符合题意.故选D.3.10解析两棵树高度差为AE=10-4=6米,两树之间的距离为BD=CE=8米,∴在Rt△ACE中,AC=√62+82=10米,即小鸟至少要飞10米.4.4.2解析设竹子折断处离地面x尺,即AC=x尺,则AB=(10-x)尺,根据题意得x2+42=(10-x)2,解得x=4.2.5.150解析如图所示,∵台阶的每一级的高为20 cm,宽为40 cm,长为90 cm,∴AB=√902+[2×(20+40)]2=150 (cm).故蚂蚁沿着台阶面从点A爬行到点B的最短路程是150 cm.6.17解析作出图形,因为东北方向和东南方向的夹角为90°,所以△ABC为直角三角形.在Rt△ABC中,AC=16×0.5=8 km,BC=30×0.5=15 km,则AB=√152+82=17 km.7.解析设旗杆的高度为x米,则绳子的长度为(x+2)米,根据勾股定理可得x2+62=(x+2)2,解得x=8.答:旗杆的高度为8米.8.解析(1)∵AB=9,BC=12,∴在Rt△ABC中,由勾股定理得AC=√AB2+BC2=√92+122=15.∴氢能源环保电动步道AC的长是15.(2)证明:∵CD=8,AD=17,AC=15,∴AD2=CD2+AC2,∴△ACD是直角三角形,且∠ACD=90°,∴AC⊥CD.9.解析(1)在Rt△ABC中,∠ABC=90°,AC=25 m,BC=7 m,∴AB=√AC2-BC2=24 m.答:这个梯子的顶端A距地面24 m.(2)在Rt△DBE中,BD=24-4=20 m,DE=25 m,∴BE=√DE2-BD2=15 m,∴CE=BE-BC=15-7=8 m.答:如果梯子的顶端下滑了4 m,那么梯子的底部在水平方向滑动了8 m.能力提升全练10.C 设水深为h尺,则芦苇长为(h+1)尺,根据勾股定理,得(h+1)2-h2=(10÷2)2,解得h=12,∴水深为12尺,故选C.11.x2+(x-6.8)2=102解析 ∵门高AB 为x 尺,∴门的宽为(x-6.8)尺,AC=1丈=10尺,依题意得AB 2+BC 2=AC 2,即x 2+(x-6.8)2=102.12.5解析 由题意可得杯子内的筷子长度最长为√122+92=15 cm, 则筷子露在杯子外面的长度最短为20-15=5(cm).13.解析 超速.由勾股定理可得BC=√AB 2-AC 2=√502-302=40(米), ∵40米=0.04千米,2秒=11 800小时, ∴小汽车的速度为0.04÷11 800=72千米/时>70千米/时.∴超速了.素养探究全练 14.解析 (1)∵AC=300 km,BC=400 km,AB=500 km, ∴AC 2+BC 2=AB 2,∴△ABC 是直角三角形,∠ACB=90°.(2)海港C 受台风影响.理由:过点C 作CD⊥AB,∵△ABC 是直角三角形,∴12×AC×BC=12×CD×AB, ∴12×300×400=12×500×CD,∴CD=240(km),∵以台风中心为圆心周围250 km以内为受影响区域,240<250, ∴海港C受台风影响.(3)当EC=250 km,FC=250 km时,正好影响C港口,∴ED=√EC2-CD2=70(km),∴EF=140 km,∵台风的速度为20千米/小时,∴140÷20=7(小时).答:台风影响该海港持续的时间为7小时.。

2022-2023学年华东师大版八年级数学上册《14.2勾股定理的应用》解答题专题提升训练（附答案）1．如图，一只小鸟旋停在空中A点，A点到地面的高度AB＝20米，A点到地面C点（B、C两点处于同一水平面）的距离AC＝25米．若小鸟竖直下降12米到达D点（D点在线段AB上），求此时小鸟到地面C点的距离．2．某海上有一小岛，为了测量小岛两端A，B的距离，测量人员设计了一种测量方法，如图，已知B是CD的中点，E是BA延长线上的一点，且∠CED＝90°，测得AE＝16.6海里，DE＝60海里．CE＝80海里．（1）求小岛两端A、B的距离；（2）过点C作CF⊥AB交AB的延长线于点F，求的值．3．如图，有一空心圆柱，高为12cm，底面周长为15cm，在圆柱内的下底面A处有一只蝴蝶，它想和上底面B处的同伴汇合，则这只蝴蝶经过的最短距离是多少cm？（π取3）4．如图，三个村庄A、B、C之间的距离分别为AB＝4km，AC＝3km，BC＝5km，要从A 修一条公路AD直达BC，已知公路的造价为26000元/km，求这条公路的最低造价是多少万元？5．（1）如图1，矩形的两邻边长分别为5和3，某一动点从点A运动到点C的最短路线长是；（2）如图2，在棱长分别为5，3，11的长方体模型中，若设定动点P从顶点C1以1个单位/秒的速度在长方体的外部沿C1→C向下匀速运动，同时动点Q从顶点A出发在长方体外部侧面上匀速运动，若要使动点Q在第5秒时恰好拦截到动点P，则动点Q的速度至少应设定为多少？6．如图，明明在距离水面高度为5m的岸边C处，用绳子拉船靠岸，开始时绳子BC的长为13m．若明明收绳6m后，船到达D处，则船向岸A移动了多少米？7．如图，有一个长方形水池，它的长是4米，池中央长了一棵芦苇，露出水面1米，将芦苇拽至池边，它的顶端刚好与水面一样平，求水有多深？芦苇有多长？8．如图，某块四边形的实验田ABCD，经测量可知∠B＝90°，AB＝24米，BC＝7米，CD ＝15米，AD＝20米．（1）判断∠D是否为直角，并说明理由．（2）求四边形ABCD的面积．9．如图，一条笔直的竹竿斜靠在一道垂直于地面的增面上，一端在墙面A处，另一端在地面B处，墙角记为点C．（1）若AB＝6.5米，BC＝2.5米．①竹竿的顶端A沿墙下滑1米，那么点B将向外移动多少米？②竹竿的顶端从A处沿墙AC下滑的距离与点B向外移动的距离，有可能相等吗？如果不可能，请说明理由；如果可能，请求出移动的距离（保留根号）．（2）若AC＝BC，则顶端A下滑的距离与底端B外移的距离，有可能相等吗？若能相等，请说明理由；若不等，请比较顶端A下滑的距离与底端B外移的距离的大小．10．如图，一架梯子AB长13米，斜靠在一面墙上，梯子底端离墙5米．（1）这个梯子的顶端距地面有多高？（2）如果梯子的顶端下滑了5米，那么梯子的底端在水平方向滑动了多少米？11．如图，一根直立的旗杆高8m，因刮大风旗杆从点C处折断，顶部B着地且离旗杆底部A4m．（1）求旗杆距地面多高处折断；（2）工人在修复的过程中，发现在折断点C的下方1.25m的点D处，有一明显裂痕，若下次大风将旗杆从点D处吹断，则距离旗杆底部周围多大范围内有被砸伤的危险？12．如图，小颖和她的同学荡秋千，秋千AB在静止位置时，下端B′离地面0.6m，荡秋千到AB的位置时，下端B距静止位置的水平距离EB等于2.4m，距地面1.4m，求秋千AB 的长．13．已知：在Rt△ABC中，∠C＝90°∠A、∠B、∠C所对的边分别记作a、b、c．如图1，分别以△ABC的三条边为边长向外作正方形，其正方形的面积由小到大分别记作S1、S2、S3，则有S1+S2＝S3；（1）如图2，分别以△ABC的三条边为直径向外作半圆，其半圆的面积由小到大分别记作S1、S2、S3，请问S1+S2与S3有怎样的数量关系，并证明你的结论；（2）分别以直角三角形的三条边为直径作半圆，如图3所示，其面积由小到大分别记作S1、S2、S3，根据（2）中的探索，直接回答S1+S2与S3有怎样的数量关系；（3）若Rt△ABC中，AC＝6，BC＝8，求出图4中阴影部分的面积．14．一艘轮船以16海里/时的速度离开港口（如图），向北偏东40°方向航行，另一艘轮船同时以12海里/时的速度向北偏西某一角度的航向行驶，已知它们离港口一个半小时后相距30海里（即BA＝30），问另一艘轮船的航行的方向是北偏西多少度？15．如图，某校科技创新兴趣小组用他们设计的机器人，在平坦的操场上进行走展示．输入指令后，机器人从出发点A先向东走10米，又向南走40米，再向西走20米，又向南走40米，再向东走70米到达终止点B．求终止点B与原出发点A的距离AB．16．如图是一个三级台阶，每级台阶都是长、宽和高分别等于90cm，25cm和15cm的长方体，A和B是这个台阶的两个相对的端点．在A点处有一只蚂蚁，想到B点去吃可口的食物，请你算一算，这只蚂蚁从A点出发，沿着台阶面爬到B点，最短路程是多少？17．一块钢板形状如图所示，量得AB＝3，BC＝4，AC＝5，CD＝12，AD＝13，请你计算一下这块钢板的面积．18．如图，圆柱形无盖玻璃容器，高18cm，底面圆的直径为cm，在外侧距下底1cm的点C处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇，试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度．（结果保留根号）19．某单位有一块四边形的空地，∠B＝90°，量得各边的长度如图（单位：米）．现计划在空地内种草，若每平方米草地造价30元，这块地全部种草的费用是多少元？20．如图，某公路稽查站设立了如下测速方法：先在公路旁选取一点C，再在笔直的车道l 上确定点D，使CD与l垂直，测得CD的长等于21m，∠ACD＝60°，∠BCD＝30°．某辆汽车从A到B用时为2s，本路段对汽车限速为40km/h，这辆汽车是否超速？说明理由．（≈1.732）参考答案1．解：由题意可知，∠B＝90°，∵AB＝20，AC＝25，∴BC＝（米），∵AD＝12，∴DB＝AB﹣AD＝20﹣12＝8（米），∴DC＝（米），即小鸟到地面C点的距离为4米．2．解：（1）在Rt△CED中，由勾股定理得：CD＝＝＝100（海里），∵∠CED＝90°，B点是CD的中点，∴BE＝CD＝×100＝50（海里），∴AB＝BE﹣AE＝50﹣16.6＝33.4（海里），答：小岛两端A、B的距离为33.4海里；（2）设BF＝x海里，∵B点是CD的中点，∴BC＝CD＝×100＝50（海里），在Rt△CFB中，由勾股定理得：CF2＝BC2﹣BF2＝502﹣x2＝2500﹣x2，在Rt△CFE中，由勾股定理得：CF2+EF2＝CE2，即2500﹣x2+（50+x）2＝802，解得：x＝14，∴＝＝．3．解：如图，将圆柱的侧面沿过A点的一条母线剪开，得到长方形ADFE，连接AB，则线段AB的长就是蝴蝶爬行的最短距离，其中C，B分别是AE，DF的中点．∵AD＝12cm，DB＝πr＝7.5cm，∴AB故蝴蝶经过的最短距离为：（cm）．答：这只蝴蝶经过的最短距离是cm．4．解：如图，由垂线段最短可知，当AD⊥BC时，这条公路的造价最低，∵AB＝4km，AC＝3km，BC＝5km，∴AB2+AC2＝25＝BC2，∴△ABC是直角三角形，且∠BAC＝90°，∴，即，解得．则这条公路的最低造价为（元）＝6.24（万元），答：这条公路的最低造价是6.24万元．5．解：（1）如图1中，连接AC．∵四边形ABCD是矩形，∴∠B＝90°，BC＝AD＝3，∴AC＝＝＝．故答案为：．（2）把长方体展开，如图3中，t＝5秒时，C1P＝5，∴CP＝CC1﹣C1P＝6，∵AC＝AB+BC＝5+3＝8，∴AP＝＝＝10，∴点Q是运动速度为＝2单位/秒．6．解：∵开始时绳子BC的长为13m．明明收绳6m后，船到达D处，∴CD＝13﹣6＝7（m），由题意得：CA⊥AB，∴∠CAB＝90°，∴AD＝＝＝2（m），AB＝＝＝12（m），∴BD＝AB﹣AD＝（12﹣2）（m），∴船向岸A移动了（12﹣2）米，答：船向岸A移动了（12﹣2）米．7．解：设水深x米，则芦苇有（x+1）米，由勾股定理：x2+22＝（x+1）2，解得：x＝1.5，x+1＝2.5，答：水深1.5米，芦苇的长度是2.5米．8．解：（1）∠D是直角，理由：连接AC，∵∠B＝90°，AB＝24米，BC＝7米，∴AC＝（米），∵CD＝15米，AD＝20米，∴CD2+AD2＝AC2，∴△ACD为直角三角形，∠D＝90°；（2）S四边形ABCD＝S△ABC+S△ACD＝＝＝234．9．解：（1）①在Rt△ABC中，AB＝6.5米，BC＝2.5米，∴AC2＝AB2﹣BC2＝6.52﹣2.52＝36，∴AC＝6米，∵AA1＝1米，∴A1C＝AC﹣AA1＝5米，在Rt△A1B1C中，A1B1＝AB＝6.5米，∴B1C2＝A1B12﹣A1C2＝6.52﹣52＝，∴B1C＝米，∴B1B＝B1C﹣BC＝﹣2.5＝米，答：点B将向外移动米；②相等．∵AC＝6米，AA1＝BB1，∴A1C＝AC﹣AA1＝6﹣AA1＝6﹣BB1，∵B1C＝BC+BB1＝2.5+BB1，B1C2＝A1B12﹣A1C2，∴（2.5+BB1）2＝6.52﹣（6﹣BB1）2，解得BB1＝3.5或0（舍去），故竹竿的顶端从A处沿墙AC下滑的距离与点B向外移动的距离会相等，移动距离为3.5米；（2）不相等．当AC＝BC时，AB＝6.5米，在Rt△ABC中，AC2+BC2＝AB2，∴AC2+BC2＝6.52，解得AC＝BC＝，在Rt△A1B1C中，B1C2+A1C2＝A1B12，即（+BB1）2+（﹣AA1）2＝6.52，解得，∴AA1＞BB1，故顶端A下滑的距离大于底端B外移的距离．10．解：（1）根据勾股定理：所以梯子距离地面的高度为：AO＝＝＝12（米）；答：这个梯子的顶端距地面有12米高；（2）梯子下滑了5米即梯子距离地面的高度为OA′＝12﹣5＝7（米），根据勾股定理：OB′＝＝＝2（米），∴BB′＝OB′﹣OB＝（2﹣5）米答：当梯子的顶端下滑5米时，梯子的底端水平后移了（2﹣5）米．11．解：（1）由题意可知：AC+BC＝8米，∵∠A＝90°，∴AB2+AC2＝BC2，又∵AB＝4米，∴AC＝3米，BC＝5米，故旗杆距地面3米处折断；（2）如图，∵D点距地面AD＝3﹣1.25＝1.75米，∴B'D＝8﹣1.75＝6.25米，∴AB′＝米，∴距离杆脚周围6米大范围内有被砸伤的危险．12．解：设AB＝AB′＝xm，由题意可得出：B′E＝1.4﹣0.6＝0.8（m），则AE＝AB﹣0.8，在Rt△AEB中，∵AE2+BE2＝AB2，∴（x﹣0.8）2+2.42＝x2解得：x＝4，答：秋千AB的长为4m．13．解：（1）∵，根据勾股定理可知：S1+S2＝S3；（2）S1+S2＝S3；（3）S阴影部分＝S1+S2﹣（S3﹣S△ABC）＝S△ABC＝×6×8＝24．14．解：由题意可知，OA＝16×1.5＝24（海里），OB＝12×1.5＝18（海里），AB＝30海里，∵242+182＝302，即OA2+OB2＝AB2，∴△OAB是直角三角形，∵∠AOD＝40°，∴∠BOD＝90°﹣40°＝50°，即另一艘轮船的航行的方向是北偏西50度．15．解：如图所示：过点A作AC⊥CB于C，则在Rt△ABC中，AC＝40+40＝80（米），BC＝70﹣20+10＝60（米），故终止点与原出发点的距离AB＝＝100（米），答：终止点B与原出发点A的距离AB为100m．16．解：展开后由题意得：∠C＝90°，AC＝3×25+3×15＝120，BC＝90，由勾股定理得：AB＝＝＝150cm，答：最短路程是150cm．17．解：∵42+32＝52，52+122＝132，即AB2+BC2＝AC2，故∠B＝90°，同理，∠ACD＝90°，∴S四边形ABCD＝S△ABC+S△ACD＝×3×4+×5×12＝6+30＝36．18．解：画圆柱的展开图，如图所示：过C作CM⊥DE于M，由题意得：BC＝DF＝1，DE＝AB＝18，∴FM＝DE﹣DF﹣ME＝18﹣1﹣1＝16，CM＝π××＝10，由勾股定理得：CF＝＝＝2，答：急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度为2cm．19．解：连接AC，∵∠B＝90°，∴在Rt△ABC中，AC2＝AB2+BC2＝32+42＝52，在△ACD中，CD2＝132，AD2＝122，∵52+122＝132，∴AC2+AD2＝CD2，∴∠DAC＝90°，∴S四边形ABCD＝S△BAC+S△DAC＝AB•BC+AC•AD＝36cm2，∵36×30＝1080（元），∴这块地全部种草的费用是1080元20．解：超速．理由：由题意得，在Rt△ADC和Rt△BCD中，∠ACD＝60°，∠BCD＝30°，∠CAD＝∠ACB＝30°，故AB＝BC，在Rt△BDC中AB＝BC＝14≈24.2（米），∵汽车从A到B用时2秒，∴速度为24.2÷2＝12.1（米/秒），∵12.1×3600＝43560（米/时），∴该车速度为43.56千米/小时，∵大于40千米/小时，∴此校车在AB路段超速．。

第14章勾股定理一、选择题（共2小题〉1.如图，在边长为1个单位长度的小正方形组成的网格中，点A、B都是格点，则线段AB的长度为（）A. 5B. 6C. 7D. 252.如图，在AABC 中，ZC二90° , AC=2,点 D 在BC±, ZADC二2ZB, AD=,则BC 的长为（）A. - 1B. +1C. - 1D. +1点E是AD的中点，且AE=1, BE的垂直平分线MN恰好过点C.则3.如图，矩形纸片ABCD中,矩形的一边AB的长度为（）A. 1B.C.D. 24. AABC中，AB二AC二5, BC二8,点P是BC边上的动点，过点P作PD丄AB于点D, PE丄AC于点E,则PD+PE的长是（）A. 4. 8B. 4. 8 或 3. 8C. 3. 8 D・ 55. 如图，在RtAABC中，ZBAC二90° , ZABC的平分线BD交AC于点D, DE是BC的垂直平分线，点E是垂足.已知DC二8, AD二4,则图中长为4 的线段有（）A. 4条B. 3条C. 2条D・1条6.如图，在四边形ABCD中，AD〃BC, DE±BC,垂足为点E,连接AC交DE于点F,点G为AF 的中点，ZACD 二2ZACB.若DG二3, ECh ,则DE 的长为（）A. 2B.C. 2D.7. 在边长为正整数的AABC中，AB二AC,且AB边上的中线CD将AABC的周长分为仁2的两部分，贝OAABC面积的最小值为（）A. B・C・ D.8. 如图，AABC中，BC二AC, D、E两点分别在BC与AC上，AD丄BC, BE丄AC, AD与BE相交于F 点.若AD二4, CD二3,则关于ZFBD、ZFCD、ZFCE的大小关系，下列何者正确？（）A. ZFBD>ZFCDB. ZFBDVZFCDC. ZFCE>ZFCDD. ZFCEVZFCD9.如图，在RtAABC中，ZACB二90°，点D是AB的中点，且CD二，如果RtAABC的面积为1,则它的周长为（）10.如图，AABC的顶点A、B、C在边长为1的正方形网格的格点上，BD丄AC于点D.则BD的长为（）A. B. C. D.二、填空题（共15小题〉门.如图，在AABC中，AB二BC二4, A0二BO, P是射线C0上的一个动点，ZA0C二60°,则当Z\PAB 为直角三角形时，AP的长为・12. 在AABC 中，AB=13cm, AC二20cm, BC 边上的高为12cm,则Z\ABC 的面积为 _____ cml13. 如图，四边形ABCD为矩形，过点D作对角线BD的垂线，交BC的延长线于点E,取BE的中点F,连接DF, DF二4.设AB二x, AD=y,贝lj x?+ （y-4）'的值为 .14. 正方形ABCD的边长是4,点P是AD边的中点，点E是正方形边上的一点.若APBE是等腰三角形，则腰长为—・15. 如图，在一张长为7cm,宽为5cm的矩形纸片上，现要剪下一个腰长为4cm的等腰三角形（要求：等腰三角形的一个顶点与矩形的一个顶点重合，其余的两个顶点在矩形的边上），则剪下的等腰三角形的面积为・16.如图，AABC中，CD丄AB于D, E是AC的中点.若AD二6, DE二5,则CD的长等于17. 等腰Z\ABC 中，AB二AC二10c叫BC=12cm,则BC 边上的高是cm.18. 已知直角三角形的两边的长分别是3和4,则第三边长为_・19. 如图，在等腰AABC中，AB=AC, BC边上的高AD二6cm,腰AB上的高CE二8cm,则Z\ABC的周长等于___ cm.20.如图，四边形ABCD 中，AB〃DC, ZB二90°,连接AC, ZDAC=ZBAC.若BC二4c叫AD二5c叫则AB 二cm.21.如图，点D在AABC的边BC上,ZC+ZBAD=ZDAC, tan Z BAD二AD 二,CD=13,则线段AC的长为22.如图，RtAABC 中，ZABC二90。

专训一：利用勾股定理巧解折叠问题名师点金：折叠图形的主要特征是折叠前后的两个图形绕着折线翻折能够完全重合，解答折叠问题就是巧用轴对称及全等的性质解答折叠中的变化规律；利用勾股定理解答折叠问题的一般步骤：(1)运用折叠图形的性质找出相等的线段或角；(2)在图形中找到一个直角三角形，然后设图形中某一线段的长为x ，将此直角三角形的三边长用数或含有x 的代数式表示出来；(3)利用勾股定理列方程求出x ；(4)进行相关计算解决问题．巧用全等法求折叠中线段的长1．(中考·泰安)如图①是一直角三角形纸片，∠A ＝30°，BC ＝4 cm ，将其折叠，使点C 落在斜边上的点C′处，折痕为BD ，如图②，再将②沿DE 折叠，使点A 落在DC′的延长线上的点A′处，如图③，则折痕DE 的长为( )(第1题)A .83 cmB ．2 3 cmC ．2 2 cmD ．3 cm巧用对称法求折叠中图形的面积2．如图所示，将长方形ABCD 沿直线BD 折叠，使点C 落在点C′处，BC′交AD 于E ，AD ＝8，AB ＝4，求△BED 的面积．(第2题)巧用方程思想求折叠中线段的长3．(2015·东莞)如图，在边长为6的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长EF交BC于点G，连接AG.(1)求证：△ABG≌△AFG；(2)求BG的长．(第3题)巧用折叠探究线段之间的数量关系4．如图，将长方形ABCD沿直线EF折叠，使点C与点A重合，折痕交AD于点E，交BC于点F，连接CE.(1)求证：AE＝AF＝EC＝CF；(2)设AE＝a，ED＝b，DC＝c，请写出一个a，b，c三者之间的数量关系式．(第4题)专训二：利用勾股定理巧求线段的最短问题名师点金：求最短距离的问题，第一种是平面图形，将分散的条件通过几何变换(轴对称)进行集中，然后借助勾股定理解决，第二种是立体图形，将立体图形展开为平面图形，在平面图形中将路程转化为两点间的距离，然后借助直角三角形利用勾股定理求出最短路程(距离)．巧用对称法、平移法求平面中的最短问题1．如图是一段楼梯的示意图，高BC是3 m，斜边AC是5 m．如果在楼梯上铺地毯，那么至少需要()长的地毯．A．5 m B．6 m C．7 m D．8 m(第1题)(第2题)2．如图，在正方形ABCD中，AB边上有一点E，AE＝3，EB＝1，在AC 上有一点P，使EP＋BP最短，则EP＋BP的最短长度是________．3．如图，A、B两个小镇在河流CD的同侧，到河的距离分别为AC＝10千米，BD＝30千米，且CD＝30千米，现在要在河边建一自来水厂，向A，B两镇供水，铺设水管的费用为每千米3万元，请你在河边CD上选择水厂的位置E，使铺设水管的费用最节省，并求出总费用．(第3题)巧用展开图法求立体图中的最短问题4．如图是一个长方体纸盒，它的长，宽，高分别为8，4，5，在盒内顶点A 处有一只壁虎，它发现盒内其对角顶点B处有一只苍蝇，于是壁虎沿盒壁向点B 爬行，求这只壁虎由点A爬行至点B的最短路程的平方．(第4题)5．已知：如图，观察图形回答下面的问题：(1)此图形的名称为________．(2)请你与同伴一起做一个这样的物体，并把它沿AS处剪开，铺在桌面上，则它的侧面展开图是一个________．(3)如果点C是SA的中点，在A处有一只蜗牛，在C处恰好有蜗牛想吃的食品，但它又不能直接爬到C处，只能沿圆锥表面爬行，你能画出蜗牛爬行的最短路线吗？(4)圆锥的母线长(SA)为10，侧面展开图的夹角为90°，请你求出蜗牛爬行的最短路程的平方．(第5题)答案专训一1．A2．解：由题意易知AD ∥BC ，∴∠2＝∠3.∵△BC′D 与△BCD 关于直线BD 对称，∴∠1＝∠2，∴∠1＝∠3，∴EB ＝ED.设EB ＝x ，则ED ＝x ，AE ＝AD －ED ＝8－x.在Rt △ABE 中，AB 2＋AE 2＝BE 2，∴42＋(8－x)2＝x 2，∴x ＝5，∴DE ＝5，∴S △BED ＝12DE·AB ＝12×5×4＝10.解题策略：解决此题的关键是证得ED ＝EB ，在Rt △ABE 中，BE 2＝AB 2＋AE 2，利用勾股定理列出方程即可求解．3．(1)证明：在正方形ABCD 中，AD ＝AB ＝BC ＝CD ，∠D ＝∠B ＝∠BCD ＝90°，∵将△ADE 沿AE 对折至△AFE ，∴AD ＝AF ，DE ＝EF ，∠D ＝∠AFE ＝90°，∴AB ＝AF ，∠B ＝∠AFG ＝90°，又∵AG ＝AG ，∴Rt △ABG ≌Rt △AFG(H .L .)．(2)解：∵△ABG ≌△AFG ，∴BG ＝FG ，设BG ＝FG ＝x ，则GC ＝6－x ，∵E 为CD 的中点，∴CE ＝EF ＝DE ＝3，∴EG ＝3＋x ，∴在Rt △CEG 中，32＋(6－x)2＝(3＋x)2，解得x ＝2，∴BG ＝2.4．(1)证明：由题意知，AF ＝CF ，AE ＝CE ，∠AFE ＝∠CFE ，又四边形ABCD 是长方形，故AD ∥BC ，∴∠AEF ＝∠CFE ，∴∠AFE ＝∠AEF ，∴AE ＝AF ＝EC ＝CF.(2)解：由题意知，AE ＝EC ＝a ，ED ＝b ，DC ＝c ，由∠D ＝90°知，ED 2＋DC 2＝CE2，即b2＋c2＝a2.专训二1．C2．5点拨：如图，连接BD交AC于O，连接ED与AC交于点P，连接BP.易知BD⊥AC，且BO＝OD，∴BP＝PD，则BP＋EP＝ED，此时最短．∵AE＝3，AD＝1＋3＝4，由勾股定理得ED2＝AE2＋AD2＝32＋42＝25＝52，∴ED＝5.即EP＋BP的最短长度为5.(第2题)(第3题)3．解：如图，作A点关于直线CD的对称点A′，连接BA′，与CD交于点E，则E点即为所求．连接AE，过点A′作A′F⊥BD交BD的延长线于F.在Rt△A′BF 中，A′B2＝A′F2＋BF2＝302＋402＝2 500，所以A′B＝50千米，故当AE＋BE＝A′B ＝50千米时，铺设水管的费用最节省，总费用为50×3＝150(万元)．4．解：将长方体中涉及点A和点B的相邻两个面展成平面图形，应有如图①②③三种可能情形，由勾股定理可知图①中，AB2＝(4＋8)2＋52＝169；图②中，AB2＝(5＋4)2＋82＝145；图③中，AB2＝(5＋8)2＋42＝185.因为185>169>145，所以最短路程的平方为145.(第4题)(第5题)5．解：(1)圆锥(2)扇形(3)如图所示，AC为蜗牛爬行的最短路线．(4)在Rt△ASC中，由勾股定理，得AC2＝102＋52＝125. 故蜗牛爬行的最短路程的平方为125.。

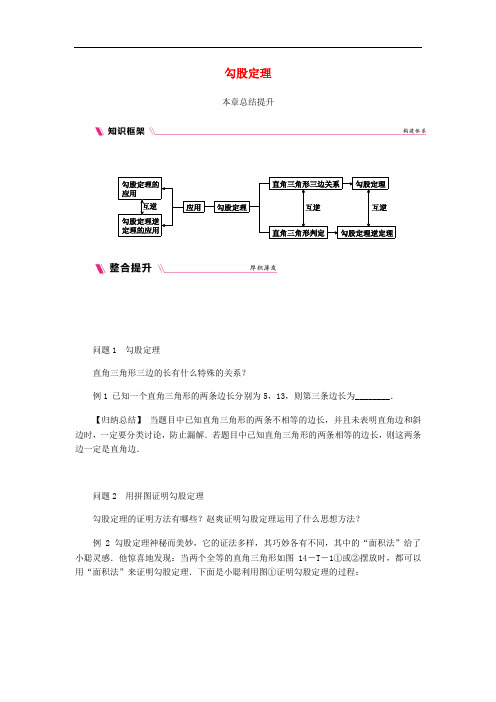
勾股定理本章总结提升问题1 勾股定理直角三角形三边的长有什么特殊的关系？例1 已知一个直角三角形的两条边长分别为5，13，则第三条边长为________．【归纳总结】当题目中已知直角三角形的两条不相等的边长，并且未表明直角边和斜边时，一定要分类讨论，防止漏解．若题目中已知直角三角形的两条相等的边长，则这两条边一定是直角边．问题2 用拼图证明勾股定理勾股定理的证明方法有哪些？赵爽证明勾股定理运用了什么思想方法？例 2 勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪灵感．他惊喜地发现：当两个全等的直角三角形如图14－T－1①或②摆放时，都可以用“面积法”来证明勾股定理．下面是小聪利用图①证明勾股定理的过程：① ②图14－T －1将两个全等的直角三角形按图①所示摆放，其中∠DAB ＝90°，求证：a 2＋b 2＝c 2. 证明：连结DB ，DC ，过点D 作BC 边上的高DF ，DF ＝EC ＝b －a . ∵S 四边形ADCB ＝S △ACD ＋S △ABC ＝12b 2＋12ab ，S 四边形ADCB ＝S △ADB ＋S △DCB ＝12c 2＋12a (b －a )，∴12b 2＋12ab ＝12c 2＋12a (b －a )． ∴a 2＋b 2＝c 2.请参照上述证法，利用图②完成下面的证明．将两个全等的直角三角形按图②所示摆放，其中∠DAB ＝90°. 求证：a 2＋b 2＝c 2.【归纳总结】 把图形进行“割”或“补”，这两种方法体现的是同一种思想——化归思想．问题3 勾股定理的应用勾股定理有哪些应用？运用勾股定理解决实际问题的关键是什么？例3 如图14－T －2所示，一架2.5米长的梯子AB 斜靠在一堵竖直的墙AO 上，这时梯脚B 到墙底端O 的距离为0.7米，如果梯子的顶端沿墙垂直下滑0.4米，那么梯脚将外移多少米？图14－T－2问题4 勾股定理与方程思想的综合运用已知一个三角形的三边长，怎样判断它是不是直角三角形？你判断的依据是什么？证明勾股定理的逆定理运用了什么方法？例4 如图14－T－3，在一棵树的10米高B处有两只猴子，其中一只爬下树走向离树20米的池塘C，而另一只爬到树顶D后直扑池塘C，结果两只猴子经过的路程相等，则这棵树有多高？图14－T－3【归纳总结】利用勾股定理建立方程是解决此类问题的关键．例5 如图14－T－4是一个三级台阶，它的每一级的长、宽和高均分别为5 dm、3 dm 和1 dm，A和B是这个台阶两个相对的端点，点A有一只蚂蚁，想到点B去吃可口的食物．请你想一想，这只蚂蚁从点A出发，沿着台阶上表面爬到点B的最短路程是______dm.图14－T－4【归纳总结】将立体图形展开为平面图形，构造直角三角形，利用勾股定理求线段的长度．例6 如图14－T－5所示，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，求这只蚂蚁要爬行的最短路程．图14－T－5【归纳总结】确定立体图形表面上两点之间的最短路程问题，解题思路是将立体图形展开，转化为平面图形，并借助勾股定理解决．当长方体的长、宽、高不同时，不同表面上两点之间的距离分三种情况讨论，展开方式不同，两点间的距离也可能不同．例7 如图14－T－6，在四边形ABCD中，已知AB∶BC∶CD∶DA＝2∶2∶3∶1，且∠B＝90°，试求∠DAB的度数．图14－T－6详解详析【整合提升】 例1 12或194例2 证明：证法一：连结BD ，过点B 作DE 边上的高BF ，则BF ＝b －a.∵S 五边形ACBED ＝S △ACB ＋S △ABE ＋S △AED ＝12ab ＋12b 2＋12ab ，S 五边形ACBED ＝S △ACB ＋S △ABD ＋S △BDE ＝12ab ＋12c 2＋12a(b －a)，∴12ab ＋12b 2＋12ab ＝12ab ＋12c 2＋12a(b －a)， ∴a 2＋b 2＝c 2.证法二：连结BD ，过点B 作DE 边上的高BF ，则BF ＝b －a. ∵S 五边形ACBED ＝S 梯形ACBE ＋S △AED ＝12b(a ＋b)＋12ab ，S 五边形ACBED ＝S △ACB ＋S △ABD ＋S △BDE ＝12ab ＋12c 2＋12a(b －a)，∴12b(a ＋b)＋12ab ＝12ab ＋12c 2＋12a(b －a)． ∴a 2＋b 2＝c 2.例3 [解析] 如图，AB ＝CD ＝2.5米，BO ＝0.7米，由勾股定理求得AO ＝2.4米．因此，OC ＝2.4－0.4＝2(米)．再由勾股定理求出OD 的长度，则可求出BD 的长度，即梯脚外移的距离．解：如图，在Rt △OAB 中，AO＝AB2－OB2＝ 2.52－0.72＝2.4(米)，OC＝2.4－0.4＝2(米)．在Rt△COD中，OD＝CD2－OC2＝ 2.52－22＝1.5(米)，∴BD＝OD－OB＝1.5－0.7＝0.8(米)．即梯脚将外移0.8米．例4解：设BD＝x米，则AD＝(10＋x)米，CD＝(30－x)米．根据题意，得(30－x)2－(10＋x)2＝202，解得x＝5.即树的高度是10＋5＝15(米)．例5[答案] 13[解析] 将台阶上表面展开，如图，因为AC＝3×3＋1×3＝12，BC＝5，所以AB2＝AC2＋BC2＝169，所以AB＝13dm，所以蚂蚁爬行的最短路程为13 dm.例6[解析] 沿长方体表面从点A爬到点B，考虑路线最短的问题有三种途径：(1)从右侧面和前面走；(2)从右侧面和上底面走；(3)从后侧面和上底面走．解：沿长方体的表面从点A爬到点B的走法有三种：(1)沿右侧面和前面走时，如图①所示，由勾股定理，得AB＝152＋202＝625＝25，即路线长l1＝25.(2)沿右侧面和上底面走时，如图②所示，由勾股定理，得AB＝（20＋5）2＋102＝725，即路线长l2＝725.(3)沿后侧面和上底面走时，如图③所示，由勾股定理，得AB＝52＋302＝925，即路线长l3＝925.因为l1＜l2＜l3，故这只蚂蚁要爬行的最短路程为25.例7解：如图，连结AC.在Rt△ABC中，∠B＝90°，且AB＝BC，所以∠BAC＝45°.由AB∶BC∶CD∶DA＝2∶2∶3∶1，设AB＝BC＝2x，CD＝3x，DA＝x.因为∠B＝90°，所以AC2＝AB2＋BC2＝8x2，所以AC2＋AD2＝8x2＋x2＝9x2＝CD2，故∠DAC＝90°，所以∠DAB＝∠BAC＋∠DAC＝135°.。

勾股定理（提高）：【学习目标】1. 掌握勾股定理的内容及证明方法，能够熟练地运用勾股定理由已知直角三角形中的两条边长求出第三条边长．2. 掌握勾股定理，能够运用勾股定理解决简单的实际问题，会运用方程思想解决问题．3. 熟练应用勾股定理解决直角三角形中的问题，进一步运用方程思想解决问题．【要点梳理】【 勾股定理 知识要点】要点一、勾股定理直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两直角边长分别为a b ，，斜边长为c ，那么222a b c +=.要点诠释：（1）勾股定理揭示了一个直角三角形三边之间的数量关系.（2）利用勾股定理，当设定一条直角边长为未知数后，根据题目已知的线段长可以建立方程求解，这样就将数与形有机地结合起来，达到了解决问题的目的.（3）理解勾股定理的一些变式：222a c b =-，222b c a =-， ()222c a b ab =+-.要点二、勾股定理的证明方法一：将四个全等的直角三角形拼成如图（1）所示的正方形.图（1）中，所以.方法二：将四个全等的直角三角形拼成如图（2）所示的正方形.图（2）中，所以.方法三：如图（3）所示，将两个直角三角形拼成直角梯形.，所以. 要点三、勾股定理的作用1. 已知直角三角形的任意两条边长，求第三边；2. 用于解决带有平方关系的证明问题；3. 利用勾股定理，作出长为的线段. 【典型例题】类型一、勾股定理的应用1、如图所示，在多边形ABCD 中，AB ＝2，CD ＝1，∠A ＝45°，∠B ＝∠D ＝90°，求多边形ABCD 的面积．【答案与解析】解：延长AD 、BC 相交于点E∵ ∠B ＝90°，∠A ＝45°∴ ∠E ＝45°，∴ AB ＝BE ＝2∵ ∠ADC ＝90°，∴ ∠DCE ＝45°，∴ CD ＝DE ＝1∴ 12222ABE S =⨯⨯=△，111122DCE S =⨯⨯=△． ∴ 13222ABE DCE ABCD S S S =-=-=△△四边形． 【总结升华】求不规则图形的面积，关键是将其转化为规则的图形（如直角三角形、正方形、等腰三角形等），转化的方法主要是割补法，然后运用勾股定理求出相应的线段，解决面积问题．举一反三：【变式】已知：如图，在△ABC，BC=2，S △ABC =3，∠ABC=135°，求AC 、AB 的长．【答案】解：如图，过点A 作AD⊥BC 交CB 的延长线于D ，在△ABC 中，∵S △ABC =3，BC=2， ∴AD===3，∵∠ABC=135°，∴∠ABD=180°﹣135°=45°， ∴AB=AD=3，BD=AD=3，在Rt△ADC 中，CD=2+3=5，由勾股定理得，AC===．2、已知直角三角形斜边长为2，周长为2【思路点拨】欲求Rt，结合勾股定理又得其平方和为4，于是可转化为用方程求解．【答案与解析】解：设这个直角三角形的两直角边长分别为a b 、，则222222a b a b ⎧++=+⎪⎨+=⎪⎩即224a b a b ⎧+=⎪⎨+=⎪⎩①②将①两边平方，得2226a ab b ++= ③ ③－②，得22ab =，所以1122ab = 因此这个直角三角形的面积为12． 【总结升华】此题通过设间接未知数a b 、，通过变形直接得出12ab 的值，而不需要分别求出a b 、 的值．本题运用了方程思想解决问题．3、长方形纸片ABCD 中，AD=4cm ，AB=10cm ，按如图方式折叠，使点B 与点D 重合，折痕为EF ，求DE 的长．【思路点拨】在折叠的过程中，BE=DE ．从而设BE 即可表示AE ．在直角三角形ADE 中，根据勾股定理列方程即可求解．【答案与解析】解：设DE=xcm ，则BE=DE=x ，AE=AB ﹣BE=10﹣x ，△ADE 中，DE 2=AE 2+AD 2，即x 2=（10﹣x ）2+16． ∴x=（cm ）．答：DE 的长为cm. 【总结升华】注意此类题中，要能够发现折叠的对应线段相等．类型二、利用勾股定理解决实际问题4、如图所示，在一棵树的10m 高的B 处有两只猴子，一只爬下树走到离树20m 处的池塘A 处，另外一只爬到树顶D 后直接跃到A 处，距离的直线计算，如果两只猴子所经过的距离相等，试问这棵树有多高？【思路点拨】其中一只猴子从B →C →A 共走了(10+20)=30m ，另一只猴子从B →D →A 也共走了30m ，并且树垂直于地面，于是这个问题可化归到直角三角形中利用勾股定理解决．【答案与解析】解：设树高CD 为x ，则BD ＝x －10，AD ＝30－(x －10)＝40－x ，在Rt △ACD 中，22220(40)x x +=-，解得：x ＝15．答：这棵树高15m ．【总结升华】本题利用距离相等用未知数来表示出DC 和DA ，然后利用勾股定理作等量关系列方程求解．举一反三：【变式】如图①，有一个圆柱，它的高等于12cm ，底面半径等于3cm ，在圆柱的底面A 点有一只蚂蚁，它想吃到上底面上与A 点相对的B 点的食物，需要爬行的最短路程是多少?(π取3)【答案】解：如图②所示，由题意可得：12AA '=，12392A B π'=⨯⨯= 在Rt △AA ′B 中，根据勾股定理得： 22222129225AB AA A B ''=+=+=则AB ＝15cm ．所以需要爬行的最短路程是15cm ．5、（2016•贵阳模拟）一架梯子长25米，斜靠在一面墙上，梯子底端离墙7米，（1）这个梯子的顶端距地面有多高？（2）如果梯子的顶端下滑了4米到A ′，那么梯子的底端在水平方向滑动了几米？【思路点拨】（1）利用勾股定理直接得出AB 的长即可；（2）利用勾股定理直接得出BC ′的长，进而得出答案．【答案与解析】解：（1）由题意得：AC=25米，BC=7米， AB==24（米），答：这个梯子的顶端距地面有24米；（2）由题意得：BA ′=20米，BC ′==15（米），则：CC ′=15﹣7=8（米），答：梯子的底端在水平方向滑动了8米．【总结升华】此题主要考查了勾股定理的应用，熟练利用勾股定理是解题关键．。

华东师大版八年级数学上册《14.1 勾股定理》练习题及答案班级：姓名：学号：分数：一、选择题1.下列各组线段能构成直角三角形的一组是( )A.5cm，9cm，12cmB.7cm，12cm，13cmC.30cm，40cm，50cmD.3cm，4cm，6cm2.由线段a、b、c组成的三角形不是直角三角形的是( )A.＝7，b＝24，c＝25；B.a＝13，b＝14，c＝15；C.a＝54，b＝1，c＝34； D.a＝41，b＝4，c＝5；3.已知一个直角三角形的两边长分别为3和4，则第三边长的平方是( )A.25B.14C.7D.7或254.Rt△ABC中，斜边BC＝2，则AB2＋AC2＋BC2的值为( )A.8B.4C.6D.无法计算5.等腰三角形的腰长为10，底长为12，则其底边上的高为( )A.13B.8C.12D.106.下列命题中，错误的是( )A.若x2＝5，则x＝5B.若a(a≥0)为有理数，则a是它的算术平方根C.化简（3－π）2的结果是π﹣3D.在直角三角形中，若两条直角边长分别是5，25，则斜边长为57.如下图中，边长k=5的直角三角形有( )A.1个B.2个C.3个D.4个8.如图所示：数轴上点A所表示的数为a，则a的值是( )A. 5 ＋1B.5﹣1C.﹣ 5 ＋1D.﹣5﹣19.如图，AE⊥AB且AE＝AB，BC⊥CD且BC＝CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是( )A.50B.62C.65D.6810.如图1是边长为1的六个小正方形组成的图形，它可以围成图2的正方体，则图1中小正方形顶点A，B在围成的正方体上的距离是( )A.0B.1C. 2D. 3二、填空题11.若三角形三边之比为3：4：5，周长为24，则三角形面积．12.如果△ABC的三边长a、b、c满足关系式(a＋2b﹣60)2＋｜b﹣18｜＋｜c﹣30｜＝0，则△ABC的形状是.13.已知a，b，c是△ABC的三边长，且满足关系式(a2－c2－b2)2＋∣c﹣b∣＝0，则△ABC的形状为_______________.14.如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝5，分别以A，B为圆心，大于1 2 AB的长为半径画弧，两弧交点分别为点P，Q，过P，Q两点作直线交BC于点D，则CD 的长是.15.已知在Rt△ABC中，∠C＝90°，若斜边c＝8，直角边a＋b＝10，则此△ABC面积为 .16.如图，在平面直角坐标系中，三角板的直角顶点P的坐标为(2，2)，一条直角边与x轴的正半轴交于点A，另一直角边与y轴交于点B，三角板绕点P在坐标平面内转动的过程中，当△POA为等腰三角形时，请写出所有满足条件的点B的坐标 .三、作图题17.分别在以下网格中画出图形．(1)在网格中画出一个腰长为10，面积为3的等腰三角形．(2)在网格中画出一个腰长为10的等腰直角三角形．四、解答题18.已知直角三角形的两条直角边长分别为a和b，斜边长为c.(1)如果a＝12，b＝5，求c；(2)如果a＝3，c＝4，求b；(3)如果c＝10，b＝9，求a.19.如图，在△ABC中，AD⊥BC，垂足为D，∠B＝60°，∠C＝45°.(1)求∠BAC的度数.(2)若AC＝2，求AD的长.20.如图，在△ABC中，AB＝17，BC＝21，AD⊥BC交边BC于点D，AD＝8，求边AC 的长.21.如图，四边形草坪ABCD中，∠B＝90°，AB＝24m，BC＝7m，CD＝15m，AD＝20m.(1)判断∠D是否是直角，并说明理由.(2)求四边形草坪ABCD的面积.22.已知,在直角三角形ABC中，∠ACB＝90°，CA＝CB，有一个圆心角为45°，半径长为CA的扇形CEF绕点C旋转，且直线CE、CF分别与直线AB交于点M、N．当扇形CEF绕点C在∠ACB的内部旋转时，如图，试说明MN2＝AM2＋BN2的理由．答案1.C.2.B.3.C4.A.5.B.6.A7.B.8.B9.A10.B11.答案为：24.12.答案为：直角三角形.13.答案为：等腰直角三角形.14.答案为：1.6.15.答案为：9；16.答案为：(0，2)，(0，0)，(0，4﹣22).17.解：(1)如图1所示：(2)如图2所示：18.解：(1)c＝a2＋b2＝122＋52＝13；(2)b＝c2－a2＝42－32＝7；(3)a＝c2－b2＝102－92＝19.19.解：(1)∠BAC＝180°﹣60°﹣45°＝75°；(2)∵AD⊥BC∴△ADC是直角三角形∵∠C＝45°∴∠DAC ＝45°∴AD ＝DC∵AC ＝2∴AD ＝ 2. 20.解：在Rt △ABD 中用勾股定理得BD 2＝AB 2﹣AD 2＝172﹣82＝225∴BD ＝15∴DC ＝6在Rt △ACD 中用勾股定理得AC 2＝AD 2＋DC 2＝100∴AC ＝10.21.解：(1)∠D 是直角，理由如下：连接AC∵∠B ＝90°，AB ＝24m ，BC ＝7m∴AC 2＝AB 2＋BC 2＝242＋72＝625∴AC ＝25(m).又∵CD ＝15m ，AD ＝20m ，152＋202＝252，即AD 2＋DC 2＝AC 2 ∴△ACD 是直角三角形，或∠D 是直角.(2)S 四边形ABCD ＝S △ABC ＋S △ADC＝12•AB •BC ＋12•AD •DC＝234(m 2).22.证明：如图，作△AMC 的对称△PMC ，连接PN ；∵∠ACB＝90°，CA＝CB，∠MCN＝45°∴∠A＝∠B＝45°，∠ACM＋∠BCN＝45°；由题意得：CP＝CA，∠ACM＝∠PCM(设为α) ∠MPC＝∠A＝45°；∵∠PCN＝45°﹣α，∠BCN＝45°﹣α∴∠PCN＝∠BCN；在△PCN与△BCN中PC＝BC，∠PCN＝∠BCN，NC＝NC∴△PCN≌△BCN(SAS)∴BN＝PN，∠NPC＝∠B＝45°∴∠MPN＝90°；由勾股定理得：MN2＝MP2＋NP2∵AM＝MP，BN＝NP∴MN2＝AM2＋BN2．。

【巩固练习】一.选择题1．如图，数轴上点A 所表示的数为a ，则a 的值是（ ）A 1B ．1C 1 D2．如图，所有三角形都是直角三角形，所有四边形都是正方形，已知S 1=4，S 2=9，S 3=8，S 4=10，则S=（ ）A ．25B ．31C ．32D ．403. 如图所示，折叠矩形ABCD 一边，点D 落在BC 边的点F 处，若AB ＝8cm ，BC ＝10cm ，EC 的长为（ ）cm ．A ．3B ．4C ．5D ．64．如图，长方形AOBC 中，点A 的坐标为（0，8)，点D 的纵坐标为3，若将矩形沿直线AD 折叠，则顶点C 恰好落在边OB 上E 处，那么图中阴影部分的面积为（ ）A. 30 B ．32 C ．34 D ．165．如图，已知△ABC 中，∠ABC ＝90°,AB ＝BC ，三角形的顶点在相互平行的三条直线1l ，2l ，3l 上，且1l ，2l 之间的距离为2 , 2l ，3l 之间的距离为3 ,则AC 的长是（ ）A ．172B ．52C ．24D ．76.（2016•漳州）如图，△ABC中，AB=AC=5,BC=8，D是线段BC上的动点（不含端点B、C）.若线段AD长为正整数，则点D的个数共有（）A．5个 B．4个C．3个D．2个二.填空题7．若一个直角三角形的两边长分别为12和5，则此三角形的第三边长为______．8. 如图，将长8cm，宽4cm的长方形纸片ABCD折叠，使点A与C重合，则折痕EF的长为__________cm.9.在△ABC中，AB=13cm，AC=20cm，BC边上的高为12cm，则△ABC的面积为cm2．10．（2016•黄冈校级自助招生）如图，它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形．如果大正方形的面积是13，小正方形的面积是1，直角三角形较短的直角边长为a，较长的直角边长为b，那么（a+b）2的值是_________ ．11. 已知长方形ABCD，AB＝3cm，AD＝4cm，过对角线BD的中点O做BD的垂直平分线EF，分别交AD、BC于点E、F，则AE的长为_______________.12．在直线上依次摆着7个正方形(如图)，已知倾斜放置的3个正方形的面积分别为1，2，3，水平放置的4个正方形的面积是1234S S S S ，，，，则1234S S S S +++=______．三.解答题13.如图所示，一架长为2.5米的梯子，斜靠在竖直的墙上，这时梯子的底端距离底0.7米，求梯子顶端离地多少米？如果梯子顶端沿墙下滑0.4m ，那么梯子底端将向左滑动多少m ？14. 现有10个边长为1的正方形，排列形式如左下图, 请把它们分割后拼接成一个新的正方形．要求： 在左下图中用实线画出分割线, 并在右下图的正方形网格图（图中每个小正方形的边长均为1）中用实线画出拼接成的新正方形.15. 将一副三角尺如图拼接：含30°角的三角尺（△ABC ）的长直角边与含45°角的三角尺（△ACD ）的斜边恰好重合．已知AB ＝2，P 是AC 上的一个动点．（1）当点P 在∠ABC 的平分线上时，求DP 的长；（2）当点PD ＝BC 时，求此时∠PDA 的度数.【答案与解析】一.选择题1.【答案】A ；【解析】－1所表示的点到点A OA 1.2.【答案】B ；【解析】解：如图，由题意得：AB 2=S 1+S 2=13，AC 2=S 3+S 4=18，∴BC 2=AB 2+AC 2=31，∴S=BC 2=31，故选B ．3.【答案】A ；【解析】设CE ＝x cm ，则DE ＝(8－x )cm ．在Rt △ABF 中，由勾股定理，得BF ＝=6cm ．∴ FC ＝10－6＝4(cm )．在Rt △EFC 中，由勾股定理，得222EF EC FC =+，即222(8)4x x -=+．解得3x =．即EC 的长为3cm ．4.【答案】A ；【解析】由题意CD ＝DE ＝5，BE ＝4，设OE ＝x ，AE ＝AC ＝4x +，所以()22284x x +=+，6x =，阴影部分面积为1168433022⨯⨯+⨯⨯=. 5.【答案】A ；【解析】如图，分别作CD ⊥3l 交2l 于点E ，作AF ⊥3l ，则可证△AFB ≌△BDC ，则AF ＝3＝BD,BF ＝CD ＝2＋3＝5，∴DF ＝5＋3＝8＝AE ，在直角△AEC 中，勾股定理得AC ＝.6. 【答案】C【解析】过点A 作AE ⊥BC,则由勾股定理得AE=3，点D 是线段BC 上的动点（不含端点B 、C ）.所以3≤AD ＜5，AD=3或4，共有3个符合条件的点.二.填空题7. 【答案】13【解析】没有指明这两边为直角边，所以要分类讨论，12也可能是斜边.8. 【答案】【解析】设AE ＝EC ＝x ，EB ＝8x -，则()22284x x -+=，解得5x =，过E 点作EH ⊥DC于H ，EH ＝4，FH ＝5－3＝2，EF =9. 【答案】126或66；【解析】解：当∠B 为锐角时（如图1），在Rt△ABD 中， BD===5cm ，在Rt△ADC 中， CD===16cm ，∴BC=21，∴S △ABC ==×21×12=126cm 2；当∠B 为钝角时（如图2），在Rt△ABD 中， BD===5cm ，在Rt△ADC 中， CD===16cm ，∴BC=CD﹣BD=16﹣5=11cm ，∴S △ABC ==×11×12=66cm 2， 故答案为：126或66．10．【答案】25；【解析】根据题意，结合勾股定理a 2+b 2=13，四个三角形的面积=4×ab=13﹣1， ∴2ab=12，联立解得：（a+b ）2=13+12=25．11.【答案】78cm ； 【解析】连接BE ，设AE ＝x ，BE ＝DE ＝4x -，则()22234x x +=-，78x =. 12．【答案】4；【解析】123413S S S S +=+=，故12344S S S S +++=.三.解答题13.【解析】解：由题意可得：AB=2.5m ，AO=0.7m ，故BO==2.4（m ）， ∵梯子顶端沿墙下滑0.4m ，∴DO=2m，CD=2.5m ，∴由勾股定理得CO=1.5m ，∴AC=CO﹣AO=1.5﹣0.7=0.8（m ）．答：梯子底端将向左滑动0.8m ．14.【解析】解：如图所示：15.【解析】解：（1）连接DP ，作DH ⊥AC ，在Rt △ABC 中，AB ＝2，∠CAB ＝30°，∴BC ＝１，AC ∵BP 是∠ABC 的角平分线，∴∠CBP ＝30°，CP .在Rt △ADC 中，DH ＝AH ＝HC ＝12AC ＝2，∴HP ＝236-=，DP ==. （2）当PD ＝BC ＝1时，P 点的位置可能有两处，分别为1P ，2P ，在Rt △1DHP 中，112HP ==， 所以∠1HDP ＝30°，∠1P DA ＝30°＋45°＝75°； 同理，∠2P DA ＝45°－30°＝15°.所以∠PDA 的度数为15°或75°.。

2022-2023学年华东师大版八年级数学上册《14.2勾股定理的应用》选择题专题提升训练（附答案）1．如图，在河道l的一侧有M，N两个村庄，现要铺设一条引水管道把河水引向M，N两个村庄．下列四种方案中，所需管道总长最短的是（）A．B．C．D．2．如图是一个圆柱形饮料罐，底面半径是3，高是4，上底面中心有一个小圆孔，则一条长10cm的直吸管露在罐外部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是（）A．5≤a≤6B．3≤a≤4C．2≤a≤3D．1≤a≤23．某工程的测量人员在规划一块如图所示的三角形土地时，在BC上有一处古建筑D，使得BC的长不能直接测出，工作人员测得AB＝130米，AD＝120米，BD＝50米，在测出AC＝150米后，测量工具坏了，使得DC的长无法测出，请你想办法求出BC的长度为（）A．90米B．120米C．140米D．150米4．如图，一架梯子AB长为5米，顶端A靠在墙AC上，这时梯子下端B与墙底端C的距离是3米，梯子下滑后停在DE的位置上，这时测得BE为1米，则梯子顶端A下滑了（）A．1米B．1.5米C．2米D．2.5米5．如图所示，甲渔船以8海里/时速度离开港口O向东北方向航行，乙渔船以6海里/时速度离开港口O向西北方向航行，同时出发，一个小时后，甲、乙两渔船相距（）海里．A．8B．10C．12D．136．如图，有一个水池，水面是一边长为8尺的正方形，在水池中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池的一边的中点，它的顶端恰好到达池边的水面，这根芦苇的长度是（）尺．A．7.5B．8C．D．97．如图，《九章算术》中记载“今有竹高一丈，末折抵地，去本三尺．问：折者高几何？”译文：一根竹子，原高一丈，虫伤有病，一阵风将竹子折断，其竹梢恰好着地，着地处离原竹子根部3尺远．问：原处还有多高的竹子？（1丈＝10尺）答：原处的竹子还有多少尺高．则高为（）A．B．C．D．8．如图，将一根长为16cm的橡皮筋固定在笔直的木棒上，两端点分别记为A，B，然后将中点C向上竖直拉升6cm至点D处，则拉伸后橡皮筋的长为（）A．20cm B．22cm C．28cm D．32cm9．如图，一艘轮船位于灯塔P北偏东60°方向，与灯塔P的距离为30海里的A处，轮船沿正南方向以每小时20海里的速度航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则此时轮船从A处到B处所用的时间为（）A．1小时B．2小时C．2.5小时D．3小时10．一个杯子的底面半径为6cm，高为16cm，则杯内所能容下的最长木棒为（）A．6cm B．12cm C．16cm D．20cm11．如图，一个圆桶底面直径为8cm，高为12cm，则桶内所能容下的最长木棒长度为（）A．8 cm B．10 cm C．4cm D．4cm 12．如图，长为12cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升8cm 至D点，则橡皮筋被拉长了（）A．5cm B．6cm C．8cm D．10cm13．如图是某学校的长方形水泥操场，如果一学生要从A角走到C角，至少走（）A．90米B．120米C．100米D．140米14．如图为某楼梯，测得楼梯的长为5米，高3米，计划在楼梯表面铺地毯，地毯的长度至少为（）A．4米B．8米C．9米D．7米15．两只蚂蚁在水平地面上从同一地点出发，一只以每分钟12cm的速度朝正东方向爬行，一只以每分钟16cm的速度朝正南方向爬行，10分钟之后两只蚂蚁相距（）A．120cm B．160cm C．200cm D．280cm16．如图，正方体的棱长为2cm，点B为一条棱的中点．蚂蚁在正方体表面爬行，从点A 爬到点B的最短路程是（）A．cm B．4cm C．cm D．5cm17．如图，有一个圆柱，它的高等于9cm，底面上圆的周长等于24cm，在圆柱下底面的点A处有一只蚂蚁，它想吃到上底面与点A相对的点B处的食物，则蚂蚁沿圆柱侧面爬行的最短路程是（）A．15cm B．17cm C．18cm D．20cm18．如图，有一架秋千，当它静止时，踏板离地0.5米，将它往前推3米时，踏板离地1.5米，此时秋千的绳索是拉直的，则秋千的长度是（）A．3米B．4米C．5米D．6米19．A，B，C三地两两的距离如图所示，B地在A地的正西方向，下面说法不正确的是（）A．C地在B地的正北方向上B．A地在B地的正东方向上C．C地在A地的北偏西60°方向上D．A地在C地的南偏东30°方向上20．如图，“赵爽弦图”是吴国的赵爽创制的．以直角三角形的斜边为边长得到一个正方形，该正方形由4个全等的直角三角形再加上中间的小正方形组成，在一次游园活动中，数学小组制作了一面“赵爽弦图锣”，其中∠AEB＝90°，AB＝13cm，BE＝5cm，则阴影部分的面积是（）A．169cm2B．25cm2C．49cm2D．64cm221．一个门框的尺寸如图所示，下列长×宽型号（单位：m）的长方形薄木板能从门框内通过的是（）A．2.6×2.5B．2.7×2.4C．2.8×2.3D．3×2.222．如图，长为16cm的橡皮筋放置在水平的x轴上，固定两端A和B，然后把中点C垂直向上拉升6cm至D点，则橡皮筋被拉长了（）A．2cm B．3cm C．4cm D．6cm23．如图，在同一水平线上有相距8m的两棵树AB和CD，其中树AB高8m，大风将树AB 折断，树的顶端B恰好落在AC的中点E处，则树的折断点离地面的高度是（）A．6m B．5m C．4m D．3m24．为预防新冠疫情，民生大院入口的正上方A处装有红外线激光测温仪（如图所示），测温仪离地面的距离AB＝2.4米，当人体进入感应范围内时，测温仪就会自动测温并报告人体体温．当身高为1.8米的市民CD正对门缓慢走到离门0.8米的地方时（即测温仪自动显示体温），则人头顶高测温仪的距离AD等于（）A．1.5米B．1.25米C．1.2米D．1.0米25．在操场上，小明沿正东方向走80m后，沿第二个方向又走了60m，再沿第三个方向走100m回到原地，小明走的第二个方向是（）A．正西方向B．东北方向C．正南方向或正北方向D．东南方向26．北京冬奥会期间，中国运动健儿取得优异成绩．冬奥会的志愿者团队，给人留下了深刻印象，人人都是志愿者．作为志愿者的小颖，从窗户向外望，看到一人为快速从A处到达居住楼B处，直接从边长为24米的正方形草地中穿过．为保护草地，小颖计划在A 处立一个标牌：“少走？米，踏之何忍”，已知B，C两处的距离为7米，那么标牌上？处的数字是（）A．3B．4C．5D．627．如图，有一个羽毛球场地是长方形ABCD，如果AB＝8m，AD＝6m．若你要从A走到C 至少要走（）A．14m B．12m C．10m D．9m28．如图，从笔直的公路l旁一点P出发，向西走6km到达l；从P出发向北走6km也到达l．下列说法错误的是（）A．公路l走向是南偏西45°B．公路l走向是北偏东45°C．从点P向北走3km后，再向西走3km到达lD．从点P向北偏西45°走3km到达l29．如图，正四棱柱的底面边长为4cm，侧棱长为6cm，一只蚂蚁从点A出发，沿棱柱外表面到点C'处吃食物，那么它需要爬行的最短路径的长是（）A．2cm B．14cm C．（2+4）cm D．10cm30．如图，长为16cm的橡皮筋放置在数轴上，固定两端A和B，然后把中点C向上拉升6cm至D点，则橡皮筋被拉长了（）A．4cm B．5cm C．6cm D．7cm参考答案1．解：依据垂线段最短，以及两点之间，线段最短，可得最节省材料的方案是：故选：B．2．解：如图，BC为饮料罐的底面直径，D为底面圆心，A为上底面中心，作射线BA、射线DA，∴AD⊥BC，AD＝4cm，BD＝CD＝3cm，∵∠ADB＝90°，∴AB＝＝＝5（cm），当吸管底端与点B重合时，则露在罐外部分a最短，此时a＝10﹣5＝5（cm）；当吸管底端与点D重合时，则露在罐外部分a最长，此时a＝10﹣4＝6（cm），∴a的取值范围是5≤a≤6，故选：A．3．解：∵AD2+BD2＝1202+502＝16900，AB2＝1302＝16900，∴AD2+BD2＝AB2，∴△ABD是直角三角形，且∠ADB＝90°，∴∠ADC＝180°﹣∠ADB＝90°，∴CD＝＝＝90（米），∴BC＝BD+CD＝50+90＝140（米），∴BC的长是140米，故选：C．4．解：∵在Rt△ABC中，AB＝5米，BC＝3米，∴AC＝＝＝4（米），在Rt△CDE中，∵DE＝AB＝5米，CE＝BC+BE＝3+1＝4（米），∴DC＝＝＝3（米），∴AD＝AB﹣DC＝4﹣3＝1（米）．答：梯子顶端A下落了1米，故选：A．5．解：∵甲渔船离开港口O向东北方向航行，乙渔船离开港口O向西北方向航行，∴∠AOB＝90°，∴出发一个小时后，OA＝8×1＝8（海里），OB＝6×1＝6（海里），∴AB＝＝＝10（海里），故选：B．6．解：设芦苇的长度为x尺，则AB的长为（x﹣1）尺，在Rt△ABC中，由勾股定理得：BC2＝AB2+AC2，即：，解得：x＝，即芦苇的长度为：尺，故选：C．7．解：设竹子折断处离地面x尺，则斜边为（10﹣x）尺，根据勾股定理得：x2+32＝（10﹣x）2，解得x＝．故选：B．8．解：Rt△ACD中，AC＝AB＝8cm，CD＝6cm；根据勾股定理，得：AD＝＝10（cm）；∴AD+BD＝2AD＝20（cm）；故拉伸后橡皮筋的长为20cm．故选：A．9．解：由题意可得：∠B＝30°，AP＝30海里，∠APB＝90°，∴AB＝2AP＝60（海里），∴轮船从A处到B处所用的时间为＝3（小时），答：则此时轮船从A处到B处所用的时间为3小时，故选：D．10．解：杯子最长对角线长为：＝20（cm），故选：D．11．解：如图，AC为圆桶底面直径，CB是桶高，∴AC＝8cm，CB＝12cm，∴线段AB的长度就是桶内所能容下的最长木棒的长度，∴AB＝＝＝4（cm）．故桶内所能容下的最长木棒的长度为4cm．故选：D．12．解：根据题意得：AD＝BD，AC＝BC，AB⊥CD，则在Rt△ACD中，AC＝AB＝6cm，CD＝8cm；根据勾股定理得：AD＝＝＝10（cm）；所以AD+BD﹣AB＝2AD﹣AB＝20﹣12＝8（cm）；即橡皮筋被拉长了8cm；故选：C．13．解：因为两点之间线段最短，所以AC的长即为从A到C的最短距离，根据矩形的对边相等，得，BC＝AD＝80米，再根据勾股定理，得，AC＝＝100（米）．故选：C．14．解：由勾股定理得：楼梯的水平宽度＝＝4（米），∵地毯铺满楼梯时其长度的和应该是楼梯的水平宽度与垂直高度的和，地毯的长度至少是3+4＝7（米）．故选：D．15．解：两只小蚂蚁10分钟所走的路程分别为120cm，160cm，∵正东方向和正南方向构成直角，∴由勾股定理得：＝200（cm），∴其距离为200cm．故选：C．16．解：如图，它运动的最短路程AB＝＝（cm）．故选：C．17．解：根据题意得出：蚂蚁沿圆柱侧面爬行的最短路程是指展开后线段AB的长，由题意得：AC＝9cm，BC＝12cm．由勾股定理得：AB＝＝＝15（cm），答：蚂蚁沿圆柱侧面爬行的最短路程是15cm．故选：A．18．解：设OA＝OB＝x米，∵BC＝DE＝3米，DC＝1.5米，∴CA＝DC﹣AD＝1.5﹣0.5＝1（米），OC＝OA﹣AC＝（x﹣1）米，在Rt△OCB中，OC＝（x﹣1）米，OB＝x米，BC＝3米，根据勾股定理得：x2＝（x﹣1）2+32，解得：x＝5，则秋千的长度是5米．故选：C．19．解：∵AB＝6km，BC＝6km，AC＝12km，∴AB2+BC2＝AC2＝144．∴△ABC是直角三角形，且∠B＝90°．∵BC＝AC，∴∠A＝30°．∴∠C＝60°．∴C地在B地的正北方向上，故选项A不符合题意；A地在B地的正东方向上，故选项B不符合题意；C地在A地的北偏西60°方向上，故选项C不符合题意；A地在C地的南偏西60°方向上，故选项D符合题意．故选：D．20．解：在Rt△ABE中，AE＝＝＝12，∵4个直角三角形是全等的，∴AH＝BE＝5，∴小正方形的边长＝AE﹣AH＝12﹣5＝7，∴阴影部分的面积＝72＝49（cm2），故选：C．21．解：连接AC，则AC与AB、BC构成直角三角形，根据勾股定理得AC＝＝＝≈2.236．四个选项中只有2，2＜2.236，∴只有3×2.2薄木板能从门框内通过，故选：D．22．解：Rt△ACD中，AC＝AB＝8cm，CD＝6cm；根据勾股定理，得：AD＝＝10（cm）；∴AD+BD﹣AB＝2AD﹣AB＝20﹣16＝4（cm）；故橡皮筋被拉长了4cm．故选：C．23．解：如图所示：根据题意可得，AE＝4m，设AF＝xm，则EF＝（8﹣x）m，在Rt△AEF中，AF2+AE2＝EF2，即x2+42＝（8﹣x）2，解得：x＝3，树的折断点离地面的高度是3m．故选：D．24．解：如图，过点D作DE⊥AB于点E，∵AB＝2.4米，BE＝CD＝1.8米，ED＝BC＝0.8米，∴AE＝AB﹣BE＝2.4﹣1.8＝0.6（米）．在Rt△ADE中，由勾股定理得到：AD＝＝＝1.0（米），故选：D．25．解：如图，AB＝80m，BC＝BD＝60m，AC＝AD＝100m，根据602+802＝1002得：∠ABC＝∠ABD＝90°，故小明向东走80m后，又走60m的方向是正南方向或正北方向，故选：C．26．解：由题意可知AB＝＝＝25（m），故居民直接到B时要走AB＝25m，若居民不践踏草地应走AC+BC＝24+7＝31（m），AC+BC﹣AB＝31﹣25＝6（m），故在？的地方应该填写的数字为6，故选：D．27．解：四边形ABCD是矩形可得∠D＝90°，CD＝AB＝8m，∴AC＝＝10（m）．∴要从A走到C，至少走10m．故选：C．28．解：如图，由题意可得△P AB是腰长6km的等腰直角三角形，则AB＝6km，如图所示，过P点作AB的垂线PC，则PC＝3km，则从点P向北偏西45°走3km到达l，选项D错误；则公路l的走向是南偏西45°或北偏东45°，选项A，B正确；则从点P向北走3km后到达BP中点D，此时CD为△P AB的中位线，故CD＝AP＝3km，故再向西走3km到达l，选项C正确．故选：D．29．解：当沿着平面ABB'A'、平面A'B'C'D'爬行时，如图所示，AC'＝＝2（cm），当沿着平面ABB'A'、平面BB'C'C爬行时，AC'＝＝10（cm），因为10＜2，所以蚂蚁需要爬行的最短路径的长是10cm，故选：D．30．解：Rt△ACD中，AC＝AB＝8cm，CD＝6cm；根据勾股定理，得：AD＝＝10（cm）；∴AD+BD﹣AB＝2AD﹣AB＝20﹣16＝4（cm）；故橡皮筋被拉长了4cm．故选：A．。