PROE九种常见曲面画法

ProE5.0曲面绘制方法第一节曲面编辑与修改曲面完成后，根据新的设计要求，可能需要对曲面进行修改与调整。

在曲面模型的建立过程中，恰当使用曲面编辑与修改工具，可提高建模效率。

本课重点练习偏移曲面、移动曲面、修剪曲面、镜像曲面、复制曲面、延伸曲面等编辑与修改工具。

一、曲面偏移曲面偏移有4种类型：“标准”、“展开”、“具有斜度”和“替代”。

在曲面偏移过程中，用户可以控制偏移的方式。

·垂直偏移：垂直于原始面进行偏移。

·自动调整：系统自动确定坐标系、比例，并沿其坐标轴控制偏移。

·控制调整：按用户定义的坐标系及指定的坐标轴来控制偏移。

·平移偏移：沿指定的方向移动曲面【练习12-1】：打开附盘“\ch12\12-1.prt”文件，使用【偏移】命令偏移复制选定的面，如图12-1所示。

图12-1 练习12-1操作示意图操作步骤提示1、选择图12-1中箭头指示的面，然后单击菜单【编辑】→【偏移】命令，打开偏移特征操控板。

2、设置偏移类型为“标准”。

3、设定偏移值为“10”，在【选项】面板中选中“侧面”选项。

【练习12-2】：打开附盘“\ch12\12-2.prt”文件，使用【偏移】命令偏移复制选定的面（偏移尺寸为25），如图12-2所示。

图12-2 练习12-2操作示意图使用展开型曲面偏移，可在选择的面之间创建连续的包容体，也可对开放曲面或实体表面的局部进行偏移。

【练习12-3】：打开附盘“\ch12\12-3.prt”文件，使用【偏移】命令偏移复制选定的面（偏移尺寸为15），如图12-3所示。

图12-3 练习12-3操作示意图操作步骤提示1、选择模型的上表面，单击菜单【编辑】→【偏移】命令，打开偏移特征操控板。

2、设置偏移类型为“展开”，设定偏移值为“15”。

3、在【控制】面板中选中“垂直偏移”选项，以垂直于上端面进行偏移。

4、在【选项】面板设置展开区域类型为“草绘区域”选项，在激活的“侧面类型”选项中选择“与草绘正交”，如图12-4所示。

PRO/E各种常见曲线方程及图示Eagles fly alone, but sheep flock together.1.碟形弹簧圓柱坐标方程：r = 5 theta = t*3600 z =(sin(3.5*theta-90))+24*t2.葉形线.笛卡儿坐標标方程：a=10x=3*a*t/(1+(t^3))y=3*a*(t^2)/(1+(t^3))3.螺旋线(Helical curve)圆柱坐标（cylindrical）方程： r=ttheta=10+t*(20*360)z=t*34.蝴蝶曲线球坐标方程：rho = 8 * t theta = 360 * t * 4 phi = -360 * t * 85.渐开线采用笛卡尔坐标系方程：r=1ang=360*ts=2*pi*r*tx0=s*cos(ang)y0=s*sin(ang)x=x0+s*sin(ang)y=y0-s*cos(ang)z=0Eagles fly alone, but sheep flock together.6.螺旋线笛卡儿坐标方程：x = 4 * cos ( t *(5*360)) y = 4 * sin ( t *(5*360))z = 10*t7.对数曲线笛卡尔坐标系方程：z=0x = 10*ty = log(10*t+0.0001)8.球面螺旋线采用球坐标系方程：rho=4theta=t*180phi=t*360*209.双弧外摆线卡迪尔坐标方程： l=2.5b=2.5x=3*b*cos(t*360)+l*cos(3*t*360) Y=3*b*sin(t*360)+l*sin(3*t*360)Eagles fly alone, but sheep flock together.10.星行线卡迪尔坐标方程：a=5x=a*(cos(t*360))^3 y=a*(sin(t*360))^311.心脏线圓柱坐标方程：a=10r=a*(1+cos(theta)) theta=t*36012.圆内螺旋线采用柱座标系方程：theta=t*360r=10+10*sin(6*theta) z=2*sin(6*theta)13.正弦曲线笛卡尔坐标系方程：x=50*ty=10*sin(t*360)z=0Eagles fly alone, but sheep flock together.14.费马曲线（有点像螺纹线）数学方程：r＊r = a*a*theta圓柱坐标方程1: theta=360*t*5a=4r=a*sqrt(theta*180/pi)方程2: theta=360*t*5a=4r=-a*sqrt(theta*180/pi)由于Pro/e只能做连续的曲线，所以只能分两做15.Talbot 曲线卡笛尔坐标方程：theta=t*360a=1.1b=0.666c=sin(theta)f=1x = (a*a+f*f*c*c)*cos(theta)/ay = (a*a-2*f+f*f*c*c)*sin(theta)/b16.Rhodonea 曲线采用笛卡尔坐标系方程：theta=t*360*4x=25+(10-6)*cos(theta)+10*cos((10/6-1)*theta)y=25+(10-6)*sin(theta)-6*sin((10/6-1)*theta)17.抛物线笛卡儿坐标方程：x =(4 * t)y =(3 * t) + (5 * t ^2)z =0Eagles fly alone, but sheep flock together.18.螺旋线圓柱坐标方程：r = 5theta = t*1800z =(cos(theta-90))+24*t19.三叶线圆柱坐标方程：a=1theta=t*380b=sin(theta)r=a*cos(theta)*(4*b*b-1)20.外摆线迪卡尔坐标方程：theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)* theta)y=(a+b)*sin(theta)-b*sin((a/b+1)* theta)z=0Eagles fly alone, but sheep flock together.21.Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta)22.长短幅圆内旋轮线卡笛尔坐标方程：a=5b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*thet a)y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)23.长短幅圆外旋轮线卡笛尔坐标方程：theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta) y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)24.三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360)) y = a*(2*sin(t*360)-sin(2*t*360))25.概率曲线！方程：笛卡儿坐标x = t*10-5y = exp(0-x^2)26.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)27.阿基米德螺线柱坐标a=100theta = t*400r = a*theta28.对数螺线柱坐标theta = t*360*2.2a = 0.005r = exp(a*theta)29.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x)for x30.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)31.双曲余弦x = 6*t-3y = (exp(x)+exp(0-x))/2Eagles fly alone, but sheep flock together.32.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/233.双曲正切x = 6*t-3y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x))34.一峰三驻点曲线x = 3*t-1.5 y=(x^2-1)^3+135.八字曲线x = 2 * cos ( t *(2*180)) y = 2 * sin ( t *(5*360)) z = 036.螺旋曲线r=t*(10*180)+1theta=10+t*(20*180)z=tEagles fly alone, but sheep flock together.37.圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 038.封闭球形环绕曲线rho=2theta=360*tphi=t*360*1039.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180)) y = 100*t * sin ( t *(5*180)) z = 040.蛇形曲线x = 2 * cos ( (t+1) *(2*180)) y = 2 * sin ( t *(5*360))z = t*(t+1)Eagles fly alone, but sheep flock together.41.8字形曲线柱坐标theta =t*360r=10+(8*sin(theta))^242.椭圆曲线笛卡尔坐标系 a = 10 b = 20theta = t*360 x = a*cos(theta) y = b*sin(theta)43.梅花曲线柱坐标theta = t*360r=10+(3*sin(theta*2.5))^244.另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2 z=4*sin(theta*3)^2Eagles fly alone, but sheep flock together.45.螺旋上升的椭圆线a = 10b = 20theta = t*360*3 x = a*cos(theta) y = b*sin(theta) z=t*1246.螺旋花曲线theta = t*360*4r=10+(3*sin(theta*2.5))^2 z = t*1647. 鼓形线笛卡尔方程r=5+3.3*sin(t*180)+t theta=t*360*10 z=t*1048. 长命锁曲线笛卡尔方程：a=1*t*359.5 b=q2*t*360c=q3*t*360 rr1=w1 rr2=w2 rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c) y=rr1*sin(a)+rr2*sin(b)+rr3*49. 簪形线球坐标 方程： rho=200*t theta=900*t phi=t*90*1050.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3 z=t^3*(t+1)51.蘑菇曲线rho=t^3+t*(t+1) theta=t*360phi=t^2*360*20*2052. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360) Y=b*sin(t*360)+a*sin(3*t*360)53.梅花曲线theta=t*360r=100+50*cos(5*theta)z=2*cos(5*theta)54.桃形曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*10*1055.名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24 56.环形二次曲线笛卡儿方程：x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)Eagles fly alone, but sheep flock together.57. 蝶线球坐标：rho=4*sin(t*360)+6*cos(t*360^2) theta=t*360phi=log(1+t*360)*t*36058.正弦周弹簧笛卡尔：ang1=t*360 ang2=t*360*20 x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2) z=sin(ang2)59.环形螺旋线x=（50+10*sin(t*360*15))*cos(t*360)y=(50+10*sin(t*360*15))*sin(t*360) z=10*cos(t*360*5)Eagles fly alone, but sheep flock together.60.内接弹簧x=2*cos(t*360*10)+cos(t*180*10) y=2*sin(t*360*10)+sin(t*180*10) z=t*661.多变内接式弹簧x=3*cos(t*360*8)-1.5*cos(t*480*8) y=3*sin(t*360*8)-1.5*sin(t*480*8) z=t*862.柱面正弦波线柱坐标：方程r=30theta=t*360z=5*sin(5*theta-90)63. ufo（漩涡线）球坐标：rho=t*20^2theta=t*log(30)*60 phi=t*7200Eagles fly alone, but sheep flock together.64. 手把曲线thta0=t*360 thta1=t*360*6 r0=400 r1=40r=r0+r1*cos(thta1) x=r*cos(thta0) y=r1*sin(thta1) z=065.篮子圆柱坐标r=5+0.3*sin(t*180)+t theta=t*360*30 z=t*566. 圆柱齿轮齿廓的渐开线方程：afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa) x=10*sin(afa)-pi*10*afa/180*cos(afa) z=0注：afa为压力角，取值范围是0到60，10为基圆半径。

第3章Pro/ENGINEER曲面绘制本章主要介绍创建曲面造型特征的一些基本和高级的方法。

基本特征的创建方式主要有拉伸、旋转、扫描、混合等；而高级特征的创建方式比较多，主要有可变截面扫描、扫描混合、螺旋扫描、边界混合、截面至曲面、曲面至曲面、从文件、自由生成等。

本章以各个曲面创建命令为主线，就生成曲面的各种方法由简单到复杂，逐步深入地介绍曲面特征的创建方法。

同时，应当指出的是，由于有关曲面操作的详细介绍在《基础篇》中已给出，所以在绘制的过程中，一些简单操作可能一笔带过，不作详细说明。

本章知识要点：•基本曲面特征设计——包括对拉伸、旋转、扫描、混合等曲面基本创建方式进行介绍。

•高级曲面特征设计——介绍可变截面扫描、扫描混合、螺旋扫描、边界混合、截面至曲面、曲面至曲面、从文件、自由生成等高级曲面创建方法。

3.1 拉伸曲面（Extrude）拉伸曲面是指一条直线或一条曲线沿其垂直于绘图平面的一个或两个相对的方向拉伸所形成的一个曲面。

下面来看看创建拉伸曲面的过程。

（1）选取【Insert】|【Extend】然后将弹出【DashBoard】（仪表板）。

（2）点选曲面按钮，然后点选草图绘制按钮进入草图绘制模式。

（3）使用草绘工具绘制拉伸曲线如图3-1所示（4）设置好拉伸深度及方向，所生成的拉伸曲面如图3-2所示。

图3-1拉伸曲线草图图3-2拉伸曲面3.2 旋转曲面（Revolve）旋转曲面是指一条直线或曲面围绕一条中心轴，按一定的角度旋转而成的一个曲面。

下面来看看旋转曲面特征的创建过程。

（1）选取【Insert】|【Revolve】，然后将在屏幕下方出现【DashBoard】（仪表板）。

（2）点选曲面按钮，然后点选草图绘制按钮进入草图绘制模式。

（3）使用草绘工具绘制旋转曲线如图3-3所示。

注意必须绘制旋转轴。

（4）设置好旋转角度及方向，所生成的旋转曲面如图3-4所示。

图3-3旋转曲线草图图3-4旋转曲面3.3 扫描曲面（Sweep）扫描曲面是指一条直线或曲线沿某一条直线或曲线路径扫描所完成的一个曲面，下面来看看扫描曲面特征的创建过程。

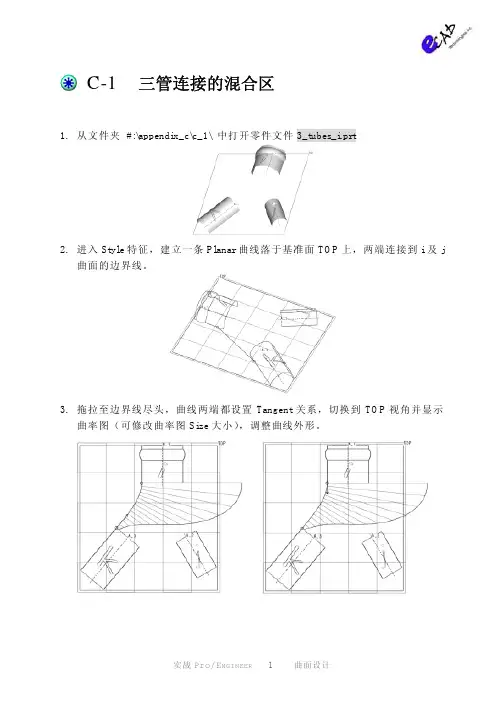
C-1 三管连接的混合区1. 从文件夹 #:\appendix_c\c_1\ 中打开零件文件3_tubes_i.prt2. 进入Style特征，建立一条Planar曲线落于基准面TOP上，两端连接到i及j曲面的边界线。

3. 拖拉至边界线尽头，曲线两端都设置Tangent关系，切换到TOP视角并显示曲率图（可修改曲率图Size大小），调整曲线外形。

4. 建立一条Free曲线，连接到i及j曲面的半圆弧边界线。

5. 切换至TOP视角，调整曲线两端点位置：在i曲面上的端点可置于半圆弧约1/4处、在j曲面上的端点可置于半圆弧约1/2处（或者设置Length Ration也可）。

两端点都必须设置Surface Tangent，显示曲率图，调整曲线外形。

6. 选用刚建立的两条曲线及两半圆弧围出曲面，进一步利用曲面连接设置，额外加上正交于基准面TOP，Length修改为10，完成后离开Style特征。

7. 依照上述步骤2~6，再建立一个Style特征，在i管与k管间建立Planar曲线、Free曲线、曲面，相关设置：Tangent、Surface Tangent等也须建立。

8. 再进入Style特征，建立一条Free曲线，两端连接到前面产生的两条Free曲线上，先在两端设定Surface Tangent于两个Style曲面再移动至曲线尽头。

不过，这条曲线外形并不容易调整到很好的情况，请读者务必多费心思！9. 建立曲面并且设置曲面连接关系，完成后离开。

10. 再建立Style特征，建立一条Planar曲线落于基准面TOP上，两端都设置Tangent。

拖拉到曲线尽头，配合曲率图调整外形。

11. 在前一个曲面上建立COS曲线，移动两端到两旁Style曲线上并调整外形（若步骤8的Free曲线外形不佳，会影响这条COS曲线）。

12. 建立曲面并额外加上正交于基准面TOP，完成后离开。

13. 目前共有7个曲面，包括原先3个i、j、k曲面。

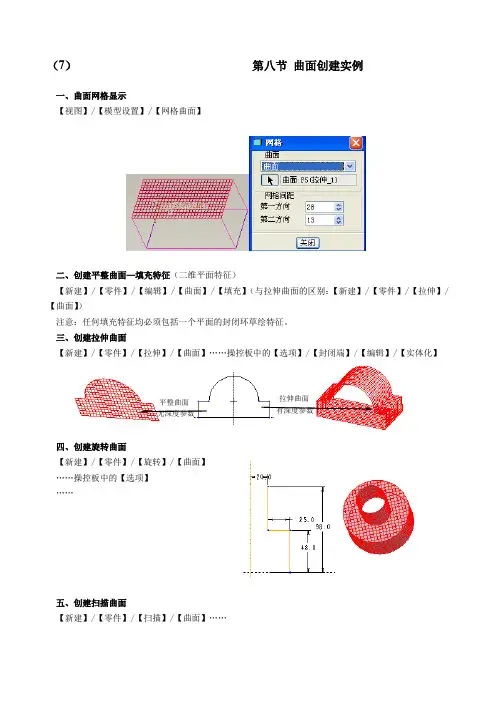
（7） 第八节 曲面创建实例一、曲面网格显示【视图】/【模型设置】/【网格曲面】二、创建平整曲面—填充特征（二维平面特征）【新建】/【零件】/【编辑】/【曲面】/【填充】（与拉伸曲面的区别：【新建】/【零件】/【拉伸】/【曲面】）注意：任何填充特征均必须包括一个平面的封闭环草绘特征。

三、创建拉伸曲面【新建】/【零件】/【拉伸】/【曲面】……操控板中的【选项】/【封闭端】/【编辑】/【实体化】四、创建旋转曲面【新建】/【零件】/【旋转】/【曲面】 ……操控板中的【选项】 ……五、创建扫描曲面【新建】/【零件】/【扫描】/【曲面】……相同的特征截面平整曲面无深度参数有深度参数拉伸曲面六、创建边界曲面边界混合曲面，即是在参照图元之间创建的混合曲面。

选取参照图元的规则如下：·曲线、棱形边、基准点、曲线、或边的端点可作为参照图元使用；·在每一个方向上，都必须按连续的顺序选择参照图元；·对于在两个方向上定义的混合曲面来说，其外部边界必须形成一个封闭的环，也就是外部边界必须相交。

边界混合曲面创建的一般过程·【文件】/【打开】/（2-SURFACE-BOUNDARY-BLENDED.PRT）P414·【插入】/【边界混合】·定义第一方向和第二方向的边界曲线（按Ctrl键选取边界曲线）例1：曲别针（paper_clip）（1）草绘曲线如图a；（2）【拉伸】创建曲面，轮廓如图b，宽度6，如图c图b样条线图c（3）将曲线投影至曲面【编辑】/【投影】一次选择曲线、曲面、基准面TOP，图d，投影曲线如图e。

图d图e（4）【插入】/【扫描混合】/【伸出项】 /【草绘截面】/【垂直于原始轨迹】/【完成】/【选取轨迹】/【依次】/【选取】，选取投影链如图f，【完成】；【自动】/【完成】，【正向】/【下一个】…输入旋转角度0，绘制截面如图g ，，绘制第二个截面，【确定】。

1、名称：正弦曲线建立环境：Pro/E软件、笛卡尔坐标系x=50*ty=10*sin(t*360)z=072、名称：螺旋线(Helical curve)建立环境：PRO/E；圆柱坐标（cylindrical）r=ttheta=10+t*(20*360)z=t*33、蝴蝶曲线球坐标PRO/E方程：rho = 8 * ttheta = 360 * t * 4phi = -360 * t * 84、Rhodonea 曲线采用笛卡尔坐标系theta=t*360*4x=25+(10-6)*cos(theta)+10*cos((10/6-1)*theta)y=25+(10-6)*sin(theta)-6*sin((10/6-1)*theta)5、圆内螺旋线采用柱座标系theta=t*360r=10+10*sin(6*theta)z=2*sin(6*theta)6、渐开线的方程r=1ang=360*ts=2*pi*r*tx0=s*cos(ang)y0=s*sin(ang)x=x0+s*sin(ang)y=y0-s*cos(ang)z=07、对数曲线z=0x = 10*ty = log(10*t+0.0001)8、球面螺旋线（采用球坐标系）rho=4theta=t*180phi=t*360*209、名称：双弧外摆线卡迪尔坐标l=2.5b=2.5x=3*b*cos(t*360)+l*cos(3*t*360) Y=3*b*sin(t*360)+l*sin(3*t*360)10、名称：星行线卡迪尔坐标a=5x=a*(cos(t*360))^3y=a*(sin(t*360))^311、名称：心脏线建立环境:pro/e,圆柱坐标a=10r=a*(1+cos(theta))theta=t*36012、名称:叶形线建立环境:笛卡儿坐标a=10x=3*a*t/(1+(t^3))y=3*a*(t^2)/(1+(t^3))13、笛卡儿坐标下的螺旋线x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t14、一抛物线s 笛卡儿坐标x =(4 * t)y =(3 * t) + (5 * t ^2)z =015、名称:碟形弹簧建立环境:pro/e 圆柱坐标r = 5z =(sin(3.5*theta-90))+24*t16、一软化弯月X=COS(360*T)+COS(2*T*360) Y=SIN(360*T)*2+SIN(360*T)*217、热带鱼笛卡儿坐标a=5x=(a*(cos(t*360*3))^4)*ty=(a*(sin(t*360*3))^4)*t18、燕尾剪笛卡儿坐标x=3*cos(t*360*4)y=3*sin(t*360*3)z=tw19、孔雀开屏球座标theta=360*t*20phi=360*t*520、一只手柱座标theta=t*360+180r=cos(360*t^3*6)*2+521、人民币符号:lol:柱座标theta=t*360+180r=cos(360*(t/(1+T^6))*6)*3+522、天蚕丝柱座标theta=t*3600r=(cos(360*t*20)*0.5*t+1)*t23、可爱的小白兔:lol:柱座标r=cos(360*(t/(1+t^(6.5)))*6*t)*3.5+524、心电图8Dr=sin(t*360*2)+0.2theta=10+t*(6*360)z=t*325、浪花一朵朵哦柱座标r=5theta=t*720z=(sin(3.5*theta-90))+2。

3.4 利用pro/e进行曲面造型曲面是一种没有厚度、质量、界限的薄膜。

一般对较规则的3D零件来说，实体特征提供了迅速且方便的造型建立方式。

但对复杂较高的造型设计而言，单单使用实体特征来建立3D 模型就显得很困难了，这是因为实体特征的造型建立方式较为固定化（如仅能使用拉伸、旋转、扫描、混合等方式来建立实体特征的造型），因此曲面特征应运而生，提供了非常弹性化的方式来建立单一曲面，然后将许多单一曲面集成为完整且没有间隙的曲面模型，通过封闭曲面转化为实体或者加厚曲面成为实体,来达到设计的目的。

它有别与实体造型,但是也和它息息相关。

曲面造型是一种用曲面表达实体形状的造型方法。

曲面特征的建立方式除了与实体特征相同的拉伸、旋转、扫描、混合等方式外，也可由点建立为曲线，再由曲线建立为曲面。

此外，曲面间也有很高的操作性，例如曲面的合并（merge），修剪（trim），延伸（extend）等（实体特征缺乏该类特征）。

由于曲面特征的使用较弹性化，因此其操作技巧性也较高3.4.1 基本曲面造型简介在造型的方法中,基本曲面由一下几种:填充、拉伸、旋转、扫描、混成。

第一种:填充曲面():以填充材料的方式构成曲面:先草绘封闭曲线,之后将在曲线边界内填充材料生成曲面,填充曲面一般为平面。

注意在pro/e中平面是有大小的,不像几何中的平面无限大,没有边界。

第二种:拉伸曲面(Extrude):拉伸曲面是指在绘图平面上的一条直线或曲线向垂直与绘图平面的一个或相对的两个方向拉伸说生成的曲面,平面是拉伸曲面最特殊的情况,结果类似与填充曲面。

第三种:旋转曲面(Revole):旋转曲面是指一条直线或曲线围绕一条中心轴线,按一定的角度旋所成的曲面(如图3-194所示图3-194第四种:扫描曲面(Sweep):扫描曲面是指一条直线或曲线(截面线)或直线或曲线(扫描路径)运动所生成的曲面,如图3-195所示。

图3-195第五种:混成曲面:混成曲面是由一系列直线或曲线的对应点串联所形成的曲面,混成曲面可根据对应点只见不同的数学过渡表达方式,可以是直线过渡,也可以是曲线过渡。