proe中曲线方程proe各种螺旋线画法教学提纲

基于Pro/E 3.0创建螺纹的三种方法——原创：哈尔滨工业大学翟万柱笔者是Pro/E的初学者，在这里仅就个人在Pro/E学习中的点滴心得与大家分享，希望大家提出宝贵意见、多多批评，以求共同进步。

螺纹机构是机械行业普遍应用的一种机构，为创建螺纹的方便Pro/E中设立有强大的螺旋扫描功能，可以实现螺纹、弹簧等基于螺旋线多种特征，其中的变节距螺旋扫描功能更是为螺旋类特征的灵活创建提供的广阔的空间，本文最后将介绍变节距弹簧的建模过程。

在掌握直接应用内建功能实现螺旋特征创建的同时，笔者认为从理论原理出发，通过基础建模功能实mouse曲面.prt.1现设想功能也是十分必要的。

不但对其他三维软件学习起到借鉴作用，同时也可以在内建功能不能满足要求的时候通过基础功能的灵活运用达到目的，并可以对Pro/E3.0的基本功能和机械基础知识增进了解。

方法一：首先，应用“插入”(Insert)>“扫描”(Sweep)>“伸出项”(Protrusion)功能进行普通梯形螺纹的建模。

想必大家对此功能都已熟悉，唯一值得讨论的地方也是重要的地方可能就是螺旋线的生成问题了。

简单易行的方法就是用方程建立曲线，而且可以容易的与参数建立关系，使得生成特征具有通用性。

常用参数方程如下：（应用时注意坐标系的选择与类型的设定）笛卡儿坐标下的螺旋线柱坐标下的螺旋线x = radia * cos ( t *(n*360)) r=radiay = radia * sin ( t * (n*360)) theta=theta0+t*(n*360)z = l*t z=t*l其中：radia为半径；n为指定长度上螺旋线的圈数；l为设定长度。

n=l/螺距；多头螺纹生成需要多条螺旋线，注意生成其他螺旋线时须设定参数方程中角度的初始值；对于左旋螺纹参数方程中角度值取负值。

生成螺旋曲线方法为：单击“插入”(Insert)>“模型基准”(Model Datum)>“曲线”(Curve)，或单击“基准”(Datum)工具栏上的按钮。

proe曲线方程式详解Proe是一种计算机辅助设计软件，可以帮助工程师设计和分析机械结构。

其中一个重要的功能就是创建和绘制曲线方程式。

本文将详细解释Proe曲线方程式的使用方法和应用场景。

1. Proe曲线方程式的定义和作用Proe曲线方程式是指通过数学表达式定义的曲线。

在Proe软件中，可以通过输入数学表达式的形式来表示曲线的形状和特征。

使用Proe曲线方程式可以方便地绘制各种复杂的曲线，如抛物线、椭圆曲线等，并对其进行调整和修改。

2. Proe曲线方程式的创建方法在Proe软件中，创建曲线方程式可以通过以下几个步骤进行：- 打开Proe软件并创建一个新的绘图文件。

- 在绘图界面选择“曲线”工具，并点击“创建曲线方程式”选项。

- 在弹出的对话框中输入数学表达式，如y=x^2，其中^表示乘方运算，即x的平方。

- 点击“确定”按钮，系统将根据输入的表达式生成相应的曲线。

3. Proe曲线方程式的应用场景Proe曲线方程式可以广泛应用于工程设计和分析领域，以下是一些常见的应用场景：- 产品设计：通过使用曲线方程式，工程师可以绘制出各种复杂形状的产品曲线，如汽车车身曲线、航空器曲线等，在产品设计过程中起到重要作用。

- 零件制造：曲线方程式在零件制造过程中也有很大的作用，工程师可以利用曲线方程式生成和调整零件的曲线轮廓，确保其符合设计要求。

- 动画效果：Proe曲线方程式还可以用于创建动画效果。

通过修改曲线方程式中的参数，可以产生各种不同的动画效果，如运动轨迹、形变动画等。

4. Proe曲线方程式的优势相比于传统的绘图方法，Proe曲线方程式具有以下几个优势：- 精确性：使用数学表达式定义曲线可以确保绘制的曲线形状精确无误，减少了绘图误差。

- 灵活性：通过修改数学表达式中的参数，可以快速调整曲线的形状和特征，提高了设计的灵活性。

- 高效性：Proe软件中的曲线方程式功能可以快速生成复杂的曲线，节省了绘图时间和人力成本。

基于PRO／E的各种螺旋线设计摘要针对螺旋线的设计，介绍了基于PRO/E的设计思路。

结合具体的设计案例，讲明了变螺距螺旋线的制作过程。

同时重点介绍了异型螺旋线的设计方法，并给出具体制作过程。

关键词PRO/E；螺旋线；设计Pro/E是美国PTC公司推出的功能强大的一款CAD/CAM/CAE集成软件，在三维建模方面有着广泛的应用。

在结构设计过程中，我们往往会遇到各种螺旋线的设计，特别是一些异型螺旋线的设计，造型往往比较复杂，这时，使用Pro/E 软件往往可以迅速达到设计要求。

Pro/E的造型能力十分强大，可以方便地按照用户的需求设计各类螺旋线，还可以实现变螺距螺旋线，椭圆螺旋线、方形螺旋线等异型螺旋线的设计。

1普通螺旋线的设计方法与普通螺旋线设计比较而言，Pro/E专门提供了一个螺旋扫描功能，可以十分方便地设计出螺旋线。

此功能可以方便的设计出变螺距螺旋线，喇叭形螺旋线，鼓形螺旋线等。

下面以图1的变螺距螺旋线为例，首先对普通螺旋线的设计过程加以说明。

1）进入Pro/E界面，点选“插入”→“螺旋扫描”→“伸出项”，在“属性”栏选取“可变螺距”和“垂直于原始轨迹”和“右手定则”。

选取草绘平面，进入草绘界面，按提示要求，绘制轨迹（注意:需要多少段不同螺距，则应绘制多少段轨迹）及螺旋线中心线后，点选“完成”。

3）输入轨迹起点和终点处的螺距值。

4）系统显示一个带有初始螺距图的子窗口，通过点选“增加点”，然后点击所画多段线段的节点，加入各段并输入螺距值。

点选“完成”，结束螺距的定义。

5）进入截面绘制界面，按图纸要求绘制螺旋线界面；点选“完成”→“确定”，即得到螺旋线。

2Pro/E设计异型螺旋线的方法在Pro/E中设计异型螺旋线的总体思路是:首先获得一个标准螺旋曲线，该螺旋线曲线的螺距应与要设计的螺旋线的螺距相同；然后通过修改螺旋线曲线的参数，或向某特定曲面投影，得到与所需螺旋线相同的螺旋曲线；最后使用变截面扫描，获得所需的螺旋线。

最全proe（creo）方程式曲线和表达式作者：登科螺旋曲线建立环境：Pro/E软件、笛卡尔坐标系半径是10，螺距是2，总长是20的螺旋线x=10*cos(t*10*360)y=10*sin(t*10*360)z=20*t名称：正弦曲线建立环境：Pro/E软件、笛卡尔坐标系x=50*ty=10*sin(t*360)z=0名称：螺旋线(Helical curve)建立环境：PRO/E；圆柱坐标（cylindrical）r=ttheta=10+t*(20*360)z=t*3蝴蝶曲线球坐标PRO/E方程：rho = 8 * ttheta = 360 * t * 4phi = -360 * t * 8Rhodonea 曲线采用笛卡尔坐标系theta=t*360*4x=25+(10-6)*cos(theta)+10*cos((10/6-1)*theta) y=25+(10-6)*sin(theta)-6*sin((10/6-1)*theta) *********************************圆内螺旋线采用柱座标系theta=t*360r=10+10*sin(6*theta)z=2*sin(6*theta)渐开线的方程r=1ang=360*ts=2*pi*r*tx0=s*cos(ang)y0=s*sin(ang)x=x0+s*sin(ang)y=y0-s*cos(ang)z=0对数曲线z=0x = 10*ty = log(10*t+0.0001)球面螺旋线（采用球坐标系）rho=4theta=t*180phi=t*360*20名称：双弧外摆线卡迪尔坐标方程：l=2.5b=2.5x=3*b*cos(t*360)+l*cos(3*t*360)Y=3*b*sin(t*360)+l*sin(3*t*360)名称：星行线卡迪尔坐标方程：a=5x=a*(cos(t*360))^3y=a*(sin(t*360))^3名稱:心臟線建立環境:pro/e,圓柱坐標a=10r=a*(1+cos(theta)) theta=t*360名稱:葉形線建立環境:笛卡儿坐標a=10x=3*a*t/(1+(t^3))y=3*a*(t^2)/(1+(t^3))笛卡儿坐标下的螺旋线x = 4 * cos ( t *(5*360)) y = 4 * sin ( t *(5*360)) z = 10*t一抛物线笛卡儿坐标x =(4 * t)y =(3 * t) + (5 * t ^2) z =0名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24*t 费马曲线（有点像螺纹线）数学方程：r＊r = a*a*theta圓柱坐标方程1: theta=360*t*5a=4r=a*sqrt(theta*180/pi)方程2: theta=360*t*5a=4r=-a*sqrt(theta*180/pi)由于Pro/e只能做连续的曲线，所以只能分两次做Talbot 曲线卡笛尔坐标方程：theta=t*360a=1.1b=0.666c=sin(theta)f=1x = (a*a+f*f*c*c)*cos(theta)/ay = (a*a-2*f+f*f*c*c)*sin(theta)/b.螺旋线圓柱坐标方程：r = 5theta = t*1800z =(cos(theta-90))+24*t三叶线圆柱坐标方程：a=1theta=t*380b=sin(theta)r=a*cos(theta)*(4*b*b-1)外摆线迪卡尔坐标方程：theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta)y=(a+b)*sin(theta)-b*sin((a/b+1)*theta)z=0Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta)长短幅圆内旋轮线卡笛尔坐标方程：a=5b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta)y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)长短幅圆外旋轮线卡笛尔坐标方程：theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta)y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360)) y = a*(2*sin(t*360)-sin(2*t*360))概率曲线！方程：笛卡儿坐标x = t*10-5y = exp(0-x^2)箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)阿基米德螺线柱坐标a=100theta = t*400r = a*theta对数螺线柱坐标theta = t*360*2.2 a = 0.005r = exp(a*theta)八字曲线x = 2 * cos ( t *(2*180))y = 2 * sin ( t *(5*360))z = 0螺旋曲线r=t*(10*180)+1theta=10+t*(20*180)z=t圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 0柱坐标螺旋曲线x = 100*t * cos ( t *(5*180))y = 100*t * sin ( t *(5*180))z = 0椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)梅花曲线柱坐标theta = t*360r=10+(3*sin(theta*2.5))^2笛卡尔方程r=5+3.3*sin(t*180)+t theta=t*360*10z=t*10环形二次曲线笛卡儿方程：x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)x=（50+10*sin(t*360*15)）*cos(t*360) y=(50+10*sin(t*360*15))*sin(t*360)z=10*cos(t*360*5)内接弹簧笛卡尔：x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*6ufo （漩涡线）球坐标：rho=t*20^2theta=t*log(30)*60 phi=t*7200手把曲线笛卡尔：thta0=t*360thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1) x=r*cos(thta0)y=r1*sin(thta1)z=0圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*5篮子圆柱齿轮齿廓的渐开线方程：笛卡尔坐标afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注：afa为压力角，取值范围是0到60，10为基圆半径笛卡尔：theta=t*360r=30+10*sin(theta*30) z=0太阳线r=1.5*cos(50*theta)+1 theta=t*360z=0迪卡尔坐标x=200*t*sin(t*3600) y=250*t*cos(t*3600) z=300*t*sin(t*1800)蕊theta = t*360r=5-(3*sin(theta*3))^2 z=(r*sin(theta*3))^2。

中曲线方程各种螺旋线画法概述螺旋线是一种具有特殊曲线形状的图形，它是由一个点沿着一定规律进行旋转或移动所形成的。

中曲线方程是描述螺旋线形状的数学方程，它可以通过绘制曲线来呈现出来。

本文将介绍一些常见的中曲线方程，并提供相应的画法。

1. Archimedean Spiral（阿基米德螺旋）阿基米德螺旋是最常见的螺旋线之一，其数学方程可以表示为：r = a + b * θ其中，r 为极坐标到原点的距离，a 和 b 是常数，θ为极坐标的角度。

这个方程描述了一个等距的螺旋线，通常以极坐标系来绘制。

画法为了绘制阿基米德螺旋，我们可以采用以下步骤：1.初始化绘图空间2.设置绘图参数，包括线条的颜色、粗细等3.循环生成一系列极坐标点4.将极坐标点转换为笛卡尔坐标系中的点5.使用绘图库绘制线条，连接转换后的点下面是一个使用 Python 的 Matplotlib 库来绘制阿基米德螺旋的示例代码：import numpy as npimport matplotlib.pyplot as plta = 0.2b = 0.1theta = np.linspace(0, 2*np.pi, 1000)r = a + b * thetax = r * np.cos(theta)y = r * np.sin(theta)plt.plot(x, y)plt.axis('equal')plt.show()2. Logarithmic Spiral（对数螺旋）对数螺旋是另一种常见的螺旋线形状，其数学方程可以表示为：r = a * exp(b * θ)其中，exp(x) 是自然对数的指数函数，a 和 b 是常数，θ是极坐标的角度。

对数螺旋的特点是，螺旋线距离原点的距离随着角度的增加呈指数增长。

画法绘制对数螺旋的方法与绘制阿基米德螺旋类似，我们需要生成一系列极坐标点，并将其转换为笛卡尔坐标系中的点。

下面是一个使用 Python 的 Matplotlib 库来绘制对数螺旋的示例代码：import numpy as npimport matplotlib.pyplot as plta = 0.05b = 0.2theta = np.linspace(0, 10*np.pi, 1000)r = a * np.exp(b * theta)x = r * np.cos(theta)y = r * np.sin(theta)plt.plot(x, y)plt.axis('equal')plt.show()3. Fermat’s Spiral（费马螺旋）费马螺旋是一种以远离原点的速度不变的方式膨胀的螺旋线，其数学方程可以表示为：r = c * sqrt(θ)其中，c 是常数，θ是极坐标的角度。

基于Pro/E 3.0创建螺纹的三种方法——原创：哈尔滨工业大学翟万柱笔者是Pro/E的初学者，在这里仅就个人在Pro/E学习中的点滴心得与大家分享，希望大家提出宝贵意见、多多批评，以求共同进步。

螺纹机构是机械行业普遍应用的一种机构，为创建螺纹的方便Pro/E中设立有强大的螺旋扫描功能，可以实现螺纹、弹簧等基于螺旋线多种特征，其中的变节距螺旋扫描功能更是为螺旋类特征的灵活创建提供的广阔的空间，本文最后将介绍变节距弹簧的建模过程。

在掌握直接应用内建功能实现螺旋特征创建的同时，笔者认为从理论原理出发，通过基础建模功能实现设想功能也是十分必要的。

不但对其他三维软件学习起到借鉴作用，同时也可以在内建功能不能满足要求的时候通过基础功能的灵活运用达到目的，并可以对Pro/E3.0的基本功能和机械基础知识增进了解。

方法一：首先，应用“插入”(Insert)>“扫描”(Sweep)>“伸出项”(Protrusion)功能进行普通梯形螺纹的建模。

想必大家对此功能都已熟悉，唯一值得讨论的地方也是重要的地方可能就是螺旋线的生成问题了。

简单易行的方法就是用方程建立曲线，而且可以容易的与参数建立关系，使得生成特征具有通用性。

常用参数方程如下：（应用时注意坐标系的选择与类型的设定）笛卡儿坐标下的螺旋线柱坐标下的螺旋线x = radia * cos ( t *(n*360)) r=radiay = radia * sin ( t * (n*360)) theta=theta0+t*(n*360)z = l*t z=t*l其中：radia为半径；n为指定长度上螺旋线的圈数；l为设定长度。

n=l/螺距；多头螺纹生成需要多条螺旋线，注意生成其他螺旋线时须设定参数方程中角度的初始值；对于左旋螺纹参数方程中角度值取负值。

生成螺旋曲线方法为：单击“插入”(Insert)>“模型基准”(Model Datum)>“曲线”(Curve)，或单击“基准”(Datum)工具栏上的按钮。

[原创教程]螺纹混合收尾教程
参考2001下螺纹柱的教程，做了这个wildfire下的螺纹教程
1 创建实体
2 螺旋扫描
3 投影-参照-选取下拉框中的-投影草绘
3.1 在草绘中用--"使用边"命令选取螺纹
3.2 绘制连接螺纹的-弧
3.3 删除--使用边--生成的螺纹
3.4 退出草绘后定义曲面和方向参照
4 扫描混合
4.1 定义一点(作为螺尾最细的口)
4.2 定义另一端的螺纹切口
5 OK了
1．如图做个圆柱
2．用螺旋扫描切除螺纹
属性定义如下
选front为草绘平面，接受系统提供的缺省参照后，进入草绘模式，绘制
如图的螺纹轨迹线
起始点设置在实体特征外部，这样可以将实体下端的螺纹切到端面，上端螺纹收尾的处理稍后给出
退出草绘模式
系统提示输入节距值：5.00
确定，再次进入草绘，绘制如图截面
退出草绘模式，确定后螺纹生成
现在要处理螺纹收尾了，用扫描混合工具，之前需先生成轨迹线选取“投影“工具，进入，投影草绘
草绘平面选front，进入
选右边的使用边工具
选择螺纹线，如图
如图绘圆弧
删去螺纹线，剩下圆弧
退出草绘
选择投影曲面如图，红色部分
如下图，选择投影方向
扫描混合工具来收尾处理
混合选项
选取轴线
然后选取刚刚投影处来的轨迹线作为轨迹线
截面角度为0，进入1截面的草绘模式，绘制一个点
退出草绘，端点类型：光滑
进入2截面，角度为0，进入草绘
绘制如图三角形
确定，就ok了
. .。

基于Pro/E 3.0创建螺纹的三种方法——原创：哈尔滨工业大学翟万柱笔者是Pro/E的初学者，在这里仅就个人在Pro/E学习中的点滴心得与大家分享，希望大家提出宝贵意见、多多批评，以求共同进步。

螺纹机构是机械行业普遍应用的一种机构，为创建螺纹的方便Pro/E中设立有强大的螺旋扫描功能，可以实现螺纹、弹簧等基于螺旋线多种特征，其中的变节距螺旋扫描功能更是为螺旋类特征的灵活创建提供的广阔的空间，本文最后将介绍变节距弹簧的建模过程。

在掌握直接应用内建功能实现螺旋特征创建的同时，笔者认为从理论原理出发，通过基础建模功能实现设想功能也是十分必要的。

不但对其他三维软件学习起到借鉴作用，同时也可以在内建功能不能满足要求的时候通过基础功能的灵活运用达到目的，并可以对Pro/E3.0的基本功能和机械基础知识增进了解。

方法一：首先，应用“插入”(Insert)>“扫描”(Sweep)>“伸出项”(Protrusion)功能进行普通梯形螺纹的建模。

想必大家对此功能都已熟悉，唯一值得讨论的地方也是重要的地方可能就是螺旋线的生成问题了。

简单易行的方法就是用方程建立曲线，而且可以容易的与参数建立关系，使得生成特征具有通用性。

常用参数方程如下：（应用时注意坐标系的选择与类型的设定）笛卡儿坐标下的螺旋线柱坐标下的螺旋线x = radia * cos ( t *(n*360)) r=radiay = radia * sin ( t * (n*360)) theta=theta0+t*(n*360)z = l*t z=t*l其中：radia为半径；n为指定长度上螺旋线的圈数；l为设定长度。

n=l/螺距；多头螺纹生成需要多条螺旋线，注意生成其他螺旋线时须设定参数方程中角度的初始值；对于左旋螺纹参数方程中角度值取负值。

生成螺旋曲线方法为：单击“插入”(Insert)>“模型基准”(Model Datum)>“曲线”(Curve)，或单击“基准”(Datum)工具栏上的按钮。

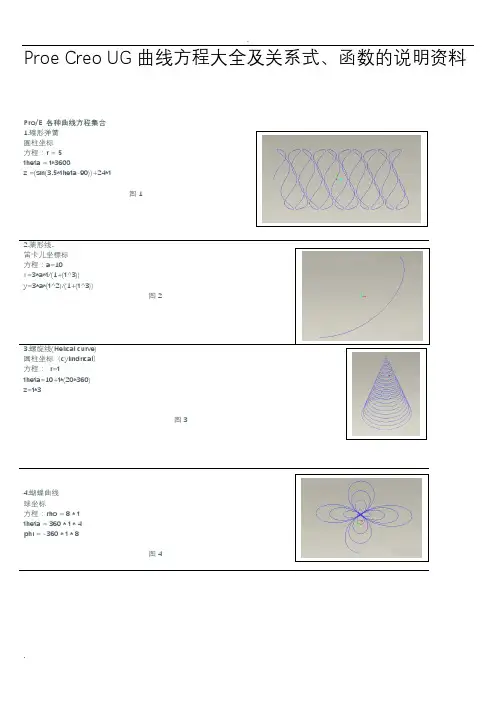
Proe Creo UG 曲线方程大全及关系式、函数的说明资料Pro/E 各种曲线方程集合 1.碟形弹簧 圓柱坐标 方程：r = 5 theta = t*3600z =(sin(3.5*theta-90))+24*t图1圆柱坐标（cylindrical ） 方程： r=ttheta=10+t*(20*360) z=t*3图34.蝴蝶曲线 球坐标方程：rho = 8 * t theta = 360 * t * 4 phi = -360 * t * 8图4图5笛卡儿坐标方程：x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t图611.心脏线圓柱坐标方程：a=10r=a*(1+cos(theta))theta=t*360Pro/E 各种曲线方程集合（二）Array22.外摆线迪卡尔坐标方程：theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta)y=(a+b)*sin(theta)-b*sin((a/b+1)*theta)z=0图22 23. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta) Array图23 24.长短幅圆内旋轮线卡笛尔坐标方程：a=5b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta)y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)图2425.长短幅圆外旋轮线卡笛尔坐标方程：theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta)y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)图2526. 三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360))y = a*(2*sin(t*360)-sin(2*t*360))图2627.概率曲线！方程：笛卡儿坐标x = t*10-5y = exp(0-x^2)图2728.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)图2829.阿基米德螺线柱坐标a=100theta = t*400r = a*theta图2930.对数螺线柱坐标theta = t*360*2.2a = 0.005r = exp(a*theta)图3031.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x)for x图3132.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)图3233.双曲余弦x = 6*t-3y = (exp(x)+exp(0-x))/2图3334.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/2图34 35.双曲正切y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x))图3536.一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3+1图3637.八字曲线x = 2 * cos ( t *(2*180))y = 2 * sin ( t *(5*360))z = 0图37r=t*(10*180)+1theta=10+t*(20*180)z=t图3839.圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 0图39 40.封闭球形环绕曲线rho=2theta=360*tphi=t*360*10图4041.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180))y = 100*t * sin ( t *(5*180))z = 0Pro/E 各种曲线方程集合（三）42.蛇形曲线x = 2 * cos ( (t+1) *(2*180))y = 2 * sin ( t *(5*360))z = t*(t+1)图4243.8字形曲线柱坐标theta = t*360r=10+(8*sin(theta))^2图4344.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)图4445.梅花曲线柱坐标theta = t*360r=10+(3*sin(theta*2.5))^2图4546.另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2z=4*sin(theta*3)^2图4647.改一下就成为空间感更强的花曲线了;)theta = t*360r=10-(3*sin(theta*3))^2z=(r*sin(theta*3))^2图4748.螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*12图4849.甚至这种螺旋花曲线theta = t*360*4r=10+(3*sin(theta*2.5))^2z = t*16图4950 鼓形线笛卡尔方程r=5+3.3*sin(t*180)+ttheta=t*360*10z=t*10图50 51 长命锁曲线笛卡尔方程：a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c)y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)图5152 簪形线球坐标方程：rho=200*ttheta=900*tphi=t*90*10图52 53.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3z=t^3*(t+1)图5354.蘑菇曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*20*20图5455. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360)Y=b*sin(t*360)+a*sin(3*t*360)图5556.梅花曲线theta=t*360r=100+50*cos(5*theta)z=2*cos(5*theta)图5657.桃形曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*10*10图5758.名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24图5859.环形二次曲线笛卡儿方程：x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)图5960 蝶线球坐标：rho=4*sin(t*360)+6*cos(t*360^2)theta=t*360phi=log(1+t*360)*t*360图6061.正弦周弹簧笛卡尔：ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2)z=sin(ang2)Pro/E 各种曲线方程集合（四）62.环形螺旋线x=（50+10*sin(t*360*15))*cos(t*360)y=(50+10*sin(t*360*15))*sin(t*360)z=10*cos(t*360*5)图6263.内接弹簧x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*6图6364.多变内接式弹簧x=3*cos(t*360*8)-1.5*cos(t*480*8)y=3*sin(t*360*8)-1.5*sin(t*480*8)z=t*8图6465.柱面正弦波线柱坐标：方程r=30theta=t*360z=5*sin(5*theta-90)图65 66. ufo （漩涡线）. 球坐标：rho=t*20^2theta=t*log(30)*60phi=t*7200图6667. 手把曲线thta0=t*360thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1)x=r*cos(thta0)y=r1*sin(thta1)z=0图6768.篮子圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*5图6869. 圆柱齿轮齿廓的渐开线方程：afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注：afa为压力角，取值范围是0到60，10为基圆半径。

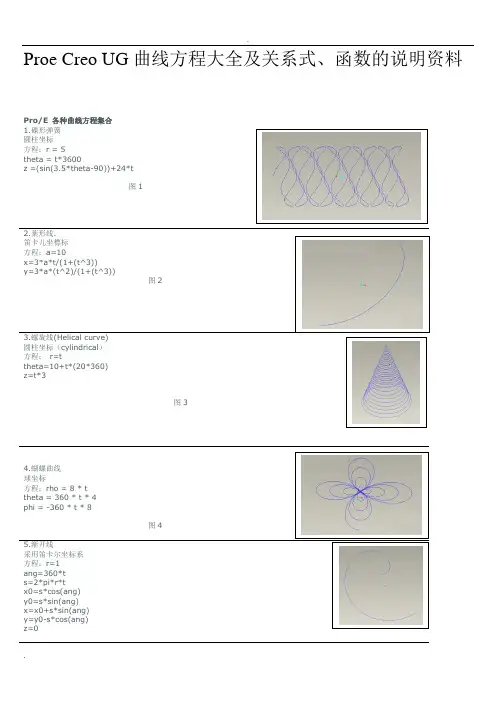
Proe Creo UG 曲线方程大全及关系式、函数的说明资料Pro/E 各种曲线方程集合 1.碟形弹簧 圓柱坐标 方程：r = 5theta = t*3600z =(sin(3.5*theta-90))+24*t图12.葉形线.圆柱坐标（cylindrical ） 方程： r=ttheta=10+t*(20*360) z=t*3图3图5笛卡儿坐标方程：x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t图611.心脏线圓柱坐标方程：a=10r=a*(1+cos(theta))theta=t*360Pro/E 各种曲线方程集合（二）Array22.外摆线迪卡尔坐标方程：theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta)y=(a+b)*sin(theta)-b*sin((a/b+1)*theta)z=0图22 23. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta)图23 24.长短幅圆内旋轮线卡笛尔坐标b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta)y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)图24 25.长短幅圆外旋轮线卡笛尔坐标方程：theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta)y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)图2526. 三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360))y = a*(2*sin(t*360)-sin(2*t*360))图26 27.概率曲线！方程：笛卡儿坐标x = t*10-5y = exp(0-x^2)图27 28.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)图28 29.阿基米德螺线柱坐标a=100theta = t*400r = a*theta图29 30.对数螺线柱坐标theta = t*360*2.2a = 0.005r = exp(a*theta)图30 31.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x)for x图31 32.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)图32 33.双曲余弦x = 6*t-3y = (exp(x)+exp(0-x))/2图33 34.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/2图34 35.双曲正切y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x))图35 36.一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3+1图36 37.八字曲线x = 2 * cos ( t *(2*180))y = 2 * sin ( t *(5*360))z = 0图37r=t*(10*180)+1theta=10+t*(20*180)z=t图38 39.圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 0图39 40.封闭球形环绕曲线rho=2phi=t*360*10图40 41.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180))y = 100*t * sin ( t *(5*180))z = 0Pro/E 各种曲线方程集合（三）42.蛇形曲线x = 2 * cos ( (t+1) *(2*180))y = 2 * sin ( t *(5*360))z = t*(t+1)图42 43.8字形曲线柱坐标theta = t*360r=10+(8*sin(theta))^2图43 44.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)图44 45.梅花曲线柱坐标theta = t*360r=10+(3*sin(theta*2.5))^2图45 46.另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2z=4*sin(theta*3)^2图46 47.改一下就成为空间感更强的花曲线了;)theta = t*360r=10-(3*sin(theta*3))^2z=(r*sin(theta*3))^2图4748.螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*12图48 49.甚至这种螺旋花曲线theta = t*360*4r=10+(3*sin(theta*2.5))^2z = t*16图49 50 鼓形线笛卡尔方程r=5+3.3*sin(t*180)+ttheta=t*360*10z=t*10图50 51 长命锁曲线笛卡尔方程：a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c)y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)图51 52 簪形线球坐标方程：rho=200*ttheta=900*tphi=t*90*10图52 53.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3z=t^3*(t+1)图53 54.蘑菇曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*20*20图54 55. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360)Y=b*sin(t*360)+a*sin(3*t*360)图55 56.梅花曲线theta=t*360r=100+50*cos(5*theta)z=2*cos(5*theta)图5657.桃形曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*10*10图57 58.名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24图58 59.环形二次曲线笛卡儿方程：x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)图59 60 蝶线球坐标：rho=4*sin(t*360)+6*cos(t*360^2)theta=t*360phi=log(1+t*360)*t*360图60 61.正弦周弹簧笛卡尔：ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2)z=sin(ang2)Pro/E 各种曲线方程集合（四）62.环形螺旋线x=（50+10*sin(t*360*15))*cos(t*360)y=(50+10*sin(t*360*15))*sin(t*360)z=10*cos(t*360*5)图62 63.内接弹簧x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*6图63 64.多变内接式弹簧x=3*cos(t*360*8)-1.5*cos(t*480*8)y=3*sin(t*360*8)-1.5*sin(t*480*8)z=t*8图64 65.柱面正弦波线柱坐标：方程r=30theta=t*360z=5*sin(5*theta-90)图65 66. ufo （漩涡线）球坐标：rho=t*20^2theta=t*log(30)*60phi=t*7200图66 67. 手把曲线thta0=t*360thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1)x=r*cos(thta0)y=r1*sin(thta1)z=0图67 68.篮子圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*5图68 69. 圆柱齿轮齿廓的渐开线方程：afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注：afa为压力角，取值范围是0到60，10为基圆半径。

proe内外螺纹的画法 proe外螺纹的画法: 1,先做个实体,(例如:φ12*100) 2,插入--螺旋扫描--伸出项,右侧点击"完成". 3,选平面--正向--缺省. 4,菜单草绘--参照--点击边缘线--画螺纹长度--中心线--挑勾完成输入节距--画牙形--挑勾完成--预览--确定. 实体螺纹生成. proe内螺纹的画法: 1,先做个实体,(例如:φ12*100) 2,插入--螺旋扫描--切口,右侧点击"完成". 3,选平面--正向--缺省. 4,菜单草绘--参照--点击边缘线--画螺纹长度--中心线--挑勾完成输入节距--画牙形--挑勾完成--正向--预览--确定. 实体内螺纹生成.
1，先做个实体，（例如：φ12*100）
2，插入--螺旋扫描--切口，右侧点击“完成”。
3，选平面--正向--缺省。
4，菜单草绘--参照--点击边缘线--画螺纹长度--中心线--挑勾完成输入节距--画牙形--挑勾完成--正向--预览--确定。
实体内螺纹生成。
proe内外ቤተ መጻሕፍቲ ባይዱ纹的画法
proe外螺纹的画法:
1，先做个实体，（例如：φ12*100）
2，插入--螺旋扫描--伸出项，右侧点击“完成”。
3，选平面--正向--缺省。
4，菜单草绘--参照--点击边缘线--画螺纹长度--中心线--挑勾完成输入节距--画牙形--挑勾完成--预览--确定。
实体螺纹生成。
Proe内螺纹的画法:

v1.0可编辑可修改Proe曲线方程大全及pro/e关系式、函数的相关说明资Pro/E各种曲线方程集合1. 碟形弹簧圓柱坐标方程：r = 5theta = t*3600z =(sin*theta-90))+24*t2. 葉形线.笛卡儿坐標标方程：a=10x=3*a*t/(1+(t A3))y=3*a*(t A2)/(1+(t A3))3. 螺旋线(Helical curve) 圆柱坐标(cylindrical ) 方程：r=ttheta=10+t*(20*360) z=t*34.蝴蝶曲线球坐标方程：rho = 8 * ttheta = 360 * t * 4phi = -360 * t * 85.渐开线采用笛卡尔坐标系方程：r=1 ang=360*ts=2*pi*r*t x0=s*cos(ang)y0=s*sin(ang) x=x0+s*sin(ang) y=y0-s*cos(a ng) z=06.螺旋线.笛卡儿坐标方程：x = 4 * cos ( t *(5*360)) y = 4 * sin ( t *(5*360))z = 10*t7.对数曲线笛卡尔坐标系方程：z=0x = 10*ty = log(10*t+8.球面螺旋线采用球坐标系方程：rho=4theta=t*180phi=t*360*209.双弧外摆线卡迪尔坐标方程：1=b=x=3*b*cos(t*360)+l*cos(3*t*360)Y=3*b*sin(t*360)+l*sin(3*t*360)10.星行线卡迪尔坐标方程：a=5x=a*(cos(t*360))A3y=a*(sin(t*360))A3图1011.心脏线圓柱坐标方程：a=10r=a*(1+cos(theta))theta=t*360v1.0可编辑可修改Pro/E 各种曲线方程集合（二）22.外摆线迪卡尔坐标theta=t*720*5方程：b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta)y=(a+b)*sin(theta)-b*sin((a/b+1)*theta)z=0图2223. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta)图2324. 长短幅圆内旋轮线卡笛尔坐标方程：a=5b=7c=theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta) y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)图2425. 长短幅圆外旋轮线卡笛尔坐标方程：theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta) y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)26. 三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360)) y = a*(2*sin(t*360)-sin(2*t*360))27. 概率曲线！方程：笛卡儿坐标x = t*10-5y = exp(0-x A2)图2728. 箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a A3/(x A2+4*a A2)图2829. 阿基米德螺线柱坐标a=100theta = t*400r = a*thetav1.0可编辑可修改图2930.对数螺线柱坐标theta = t*360*a =r = exp(a*theta)图3031.蔓叶线笛卡儿坐标系a=10v1.0可编辑可修改y=t*100-50 solvex A3 = yA2*(2*a-x)for x图31曲线笛卡儿坐标系x = t*y = tan(x*20)v1.0可编辑可修改图3233.双曲余弦x = 6*t-3y = (exp(x)+exp(0_x))/2图3334.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/2图3435. 双曲正切x = 6*t-3 y = (exp(x)-exp(O-x))/(exp(x)+exp(O-x))图3536. 一峰三驻点曲线x = 3*y=(x A2-1)A3+1图3637. 八字曲线x = 2 * cos ( t *(2*180))y = 2 * sin ( t *(5*360))z = 038. 螺旋曲线r=t*(10*180)+1 theta=10+t*(20*180)z=t图3839. 圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 040. 封闭球形环绕曲线rho=2theta=360*t phi=t*360*10图4041. 柱坐标螺旋曲线x = 100*t * cos ( t *(5*180))y = 100*t * sin ( t *(5*180))Pro/E各种曲线万程集合(三) 42. 蛇形曲线x = 2 * cos ( (t+1) *(2*180)) y = 2 * sin ( t *(5*360))z = t*(t+1)字形曲线柱坐标theta = t*360r=10+(8*sin(theta))A2图4344.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta) y = b*sin(theta)图4445.梅花曲线柱坐标theta = t*360r=10+(3*sin(theta*F2图4546.另一个花曲线theta = t*360r=10-(3*sin(theta*3))A2z=4*sin(theta*3)A2图4647. 改一下就成为空间感更强的花曲线了；theta = t*360 r=10-(3*sin(theta*3)F2z=(r*sin(theta*3)F2图4748. 螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*12图4849. 甚至这种螺旋花曲线theta = t*360*4 r=10+(3*sin(theta*F2 z = t*16图4950鼓形线笛卡尔方程r=5+*sin(t*180)+ttheta=t*360*10z=t*10图5051长命锁曲线笛卡尔方程：a=1*t*b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c)y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)图5152簪形线球坐标方程：rho=200*ttheta=900*t phi=t*90*10图5253. 螺旋上升曲线r=t A10theta=tA3*360*6*3+U3*360*3*3 z=t A3*(t+1)图5354. 蘑菇曲线rho=tA3+t*(t+1)theta=t*360 phi=tA2*360*20*20图5455. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360)Y=b*sin(t*360)+a*sin(3*t*360)ff5556. 梅花曲线theta=t*360r=100+50*cos(5*theta)z=2*cos(5*theta)图5657. 桃形曲线rho=t A3+t*(t+1)theta=t*360phi=tA2*360*10*10v1.0可编辑可修改图5758. 名稱：碟形弹簧建立環境：pro/e圓柱坐r = 5theta = t*3600z =(sin*theta-90))+24图5859. 环形二次曲线笛卡儿方程：x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)图5960蝶线球坐标：rho=4*sin(t*360)+6*cos(t*360A2)theta=t*360phi=log(1+t*360)*t*360图661. 正弦周弹簧笛卡尔：ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2)z=sin(ang2)Pro/E各种曲线方程集合（四）62. 环形螺旋线x= (50+10*sin(t*360*15))*cos(t*360)y=(50+10*sin(t*360*15))*sin(t*360)z=10*cos(t*360*5)图62 63. 内接弹簧x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*6图63 64. 多变内接式弹簧x=3*cos(t*360*8)*cos(t*480*8)y=3*sin(t*360*8)*sin(t*480*8)z=t*8图6465. 柱面正弦波线柱坐标：方程r=30theta=t*360z=5*sin(5*theta-90)图65 66. ufo (漩涡线)球坐标：rho=t*20A2theta=t*log(30)*60phi=t*7200图6667. 手把曲线thta0=t*360thta 1=t*360*6r0=400r1=40 r=r0+r1*cos(thta1) x=r*cos(thta0) y=r1*sin(thta1) z=0图6768. 篮子圆柱坐标r=5+*sin(t*180)+ttheta=t*360*30z=t*5图6869. 圆柱齿轮齿廓的渐开线方程：afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注：afa为压力角，取值范围是0到60, 10为基圆半径。

如何製作螺旋線（Helical Curve）製作螺旋線有下列二個方法：1、formed curve；2、利用方程式（from equation）一.Formed curve：1、首先建立缺省的datum plan；並建立一個參數p，用來控制螺旋圈數（setup/parameters/create/real parameters ,初始值可以設為：1）2、建立圓柱體（或者圓柱曲面），如圖1：圖13、建立form curve,選擇tang plane 為sketching plane,選擇圓柱體的頂面為top,然後繪製如圖2直線：圖2注意事項：a、對齊直線的兩個端點（右上端點對齊圓柱的top面，左下端點對齊圓柱軸線和tang plane的交點）b、建立coordinate system，並對齊直線的左下端點)4、建立relation：sd#=L*P*PI*D[L為圓柱的長度；P 為參數（第一步建立的參數）； D 為圓柱的直徑；PI 為π]5、regenerate後你可以看到生成的helical curve(圖3)了。

圖3二、利用方程式：1、首先建立缺省的datum plan，coordinate system(系統座標)2、建立datum curve ,選擇 from equation3、選擇coordinate system, 圓柱座標（cylindrical）卡笛爾座標(Cartesian)球座標(sphereical)此時出現下列資訊：/* For cylindrical coordinate system, enter parametric equation/* in terms of t (which will vary from 0 to 1) for r, theta and z/* For example: for a circle in x-y plane, centered at origin/* and radius = 4, the parametric equations will be:/* r = 4/* theta = t * 360/* z = 0/*-------------------------------------------------------------------其中螺旋線的方程式為：r = 螺旋線的最小半徑 + t * (螺旋線的主要半徑-螺旋線的最小半徑)theta = t * (螺旋線的螺距 * 360 * 引導角的度數 (if any) z = 要求高度 + t在彈出的資訊文檔內輸入下列數值：4、存檔退出後按ok5、你所建立的螺旋線如下圖：。

结束语
感谢收看本课程，希望你 已经学到了有用的知识和 技能。
了解不同类型的螺纹的特点和绘制
方法。掌握如何使用Proe软件绘制
螺纹。
3
步骤三：绘制螺帽
介绍了螺帽的种类和绘制方法。具
体讲解了如何利用Proe画出螺帽的
步骤四：添加标注
4
轮廓和细节。
讲解了螺栓图的标注方式以及标注 的作用和规范。
注意事项
1 绘图的技巧
讲解了螺栓绘图中常见的技巧和窍门，以及如何使用Proe软件快速完成螺栓图。
Proe螺栓的画法
这是一份关于Proe螺栓绘图技巧的PPT课件。在这个课程中，你将学习如何使 用Proe软件绘制高品质的螺栓图。本课程旨在帮助你了解螺栓的基础知识并 掌握绘图技巧，以便在工程设计中更好地应用它们。
介绍
课程概述
介绍了课程内容和目标， 引导Hale Waihona Puke 制定课程学习计 划。学习目标
掌握螺栓的定义、螺纹 的种类和螺栓的类型； 使用Proe软件绘制螺栓 图；了解螺栓绘图技巧， 提高螺栓绘图效率。
2 绘图中常见错误及解决方法
针对螺栓绘图容易出现的问题，介绍了常见错误的原因和解决方法。
3 完成绘图后的检查
解释了如何对绘制好的螺栓图进行检查，以确保它满足设计要求。
课程总结
知识回顾
回顾本课程的重点内容， 总结螺栓基础知识和绘图 技巧。
课程展望
展望将来的学习方向，包 括更高级的螺栓绘图知识 和其他工程设计技术。
螺栓的定义
了解螺栓的组成、结构和用 途。
螺纹的种类
介绍了常见的螺纹类型，如 普通螺纹、紧固螺纹、管螺 纹等。
螺栓的类型
讲解了各种类型螺栓的区别 和用途，如传统螺栓、结构 螺栓、联接螺栓等。

总结词
调整材质和纹理
详细描述
为了提高螺栓的渲染效果，可以调整材质和纹理，如金属 光泽、表面粗糙度等，以呈现更加真实的视觉效果。同时 ，还可以使用贴图来增加细节和质感。
总结词
使用高级渲染技巧
详细描述
为了获得更加出色的渲染效果，可以学习并运用一些高级 渲染技巧，如景深、运动模糊和辉光等，以增强螺栓的视 觉冲击力。
优化渲染效果
总结词
优化渲染效果可以提升螺栓的可视化效果和真实感，使其更加逼真和具有吸引力。
详细描述
在Proe中，用户可以使用高级渲染功能来优化螺栓的渲染效果。通过调整光照、阴影、材质等参数， 可以创造出更加逼真的视觉效果，使螺栓更加引人注目。此外，还可以使用贴图、纹理等素材来增强 螺栓的细节和质感，提高整体的美观度。
详细描述：为了提高螺栓画法的效率和准确性，建议使 用Proe提供的模板进行绘制。这些模板已经预设了正 确的参数和尺寸，可以避免手动调整时出现误差。
如何提高螺栓画法的渲染效果？
总结词
选择合适的渲染器
详细描述
在Proe中，可以选择不同的渲染器来提高螺栓的渲染效 果。根据需要选择合适的渲染器，如光线追踪或全局照明 渲染器，以获得更加逼真的渲染效果。
总结词
基础操作，掌握基本流程
VS
详细描述
介绍如何使用Proe软件绘制标准螺栓， 包括创建基本圆柱体、切割圆柱体、创建 螺纹等步骤，强调操作流程的规范性和准 确性。
案例二：特殊形状螺栓的绘制
总结词
进阶技巧，创意设计
详细描述
介绍如何绘制具有特殊形状的螺栓，如异形 螺栓、带孔螺栓等，通过实例演示如何运用 Proe的参数化建模和特征创建功能，实现 创意设计。
批量处理和自动化

Proe Creo UG曲线方程大全与关系式、函数的说明资料Pro/E 各种曲线方程集合1.碟形弹簧圓柱坐标方程：r = 5theta = t*3600z =<sin<3.5*theta-90>>+24*t图12.葉形线.笛卡儿坐標标方程：a=10x=3*a*t/<1+<t^3>>y=3*a*<t^2>/<1+<t^3>>图23.螺旋线<Helical curve>圆柱坐标〔cylindrical〕方程：r=ttheta=10+t*<20*360>z=t*3图34.蝴蝶曲线球坐标方程：rho = 8 * ttheta = 360 * t * 4phi = -360 * t * 8图45.渐开线采用笛卡尔坐标系方程：r=1ang=360*ts=2*pi*r*tx0=s*cos<ang>y0=s*sin<ang>x=x0+s*sin<ang>y=y0-s*cos<ang>z=0图56.螺旋线.笛卡儿坐标方程：x = 4 * cos < t *<5*360>>y = 4 * sin < t *<5*360>>z = 10*t图6 7.对数曲线笛卡尔坐标系方程：z=0x = 10*ty = log<10*t+0.0001>图78.球面螺旋线采用球坐标系方程：rho=4theta=t*180phi=t*360*20图8 9.双弧外摆线卡迪尔坐标方程：l=2.5b=2.5x=3*b*cos<t*360>+l*cos<3*t*360>Y=3*b*sin<t*360>+l*sin<3*t*360>图910.星行线卡迪尔坐标方程：a=5x=a*<cos<t*360>>^3y=a*<sin<t*360>>^3图10 11.心脏线圓柱坐标方程：a=10r=a*<1+cos<theta>>theta=t*360Pro/E 各种曲线方程集合〔二〕22.外摆线迪卡尔坐标方程：theta=t*720*5b=8a=5x=<a+b>*cos<theta>-b*cos<<a/b+1>*theta>y=<a+b>*sin<theta>-b*sin<<a/b+1>*theta>z=0图22 23. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin<n*theta+c>y=b*sin<theta>图23 24.长短幅圆内旋轮线卡笛尔坐标方程：a=5b=7c=2.2theta=360*t*10x=<a-b>*cos<theta>+c*cos<<a/b-1>*theta>y=<a-b>*sin<theta>-c*sin<<a/b-1>*theta>图24 25.长短幅圆外旋轮线卡笛尔坐标方程：theta=t*360*10a=5b=3c=5x=<a+b>*cos<theta>-c*cos<<a/b+1>*theta>y=<a+b>*sin<theta>-c*sin<<a/b+1>*theta>图25 26. 三尖瓣线a=10x = a*<2*cos<t*360>+cos<2*t*360>>y = a*<2*sin<t*360>-sin<2*t*360>>图26 27.概率曲线！方程：笛卡儿坐标x = t*10-5y = exp<0-x^2>图27 28.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/<x^2+4*a^2>图28 29.阿基米德螺线柱坐标a=100theta = t*400r = a*theta图29 30.对数螺线柱坐标theta = t*360*2.2a = 0.005r = exp<a*theta>图30 31.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*<2*a-x>for x图31 32.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan<x*20>图32 33.双曲余弦x = 6*t-3y = <exp<x>+exp<0-x>>/2图33 34.双曲正弦x = 6*t-3y = <exp<x>-exp<0-x>>/2图34 35.双曲正切x = 6*t-3y = <exp<x>-exp<0-x>>/<exp<x>+exp<0-x>>图35 36.一峰三驻点曲线x = 3*t-1.5y=<x^2-1>^3+1图36 37.八字曲线x = 2 * cos < t *<2*180>>y = 2 * sin < t *<5*360>>z = 0图37 38.螺旋曲线r=t*<10*180>+1theta=10+t*<20*180>z=t图38 39.圆x = cos < t *<5*180>>y = sin < t *<5*180>>z = 0图39 40.封闭球形环绕曲线rho=2theta=360*tphi=t*360*10图40 41.柱坐标螺旋曲线x = 100*t * cos < t *<5*180>>y = 100*t * sin < t *<5*180>>z = 0Pro/E 各种曲线方程集合〔三〕42.蛇形曲线x = 2 * cos < <t+1> *<2*180>>y = 2 * sin < t *<5*360>>z = t*<t+1>图42 43.8字形曲线柱坐标theta = t*360r=10+<8*sin<theta>>^2图43 44.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos<theta>y = b*sin<theta>图44 45.梅花曲线柱坐标theta = t*360r=10+<3*sin<theta*2.5>>^2图45 46.另一个花曲线theta = t*360r=10-<3*sin<theta*3>>^2z=4*sin<theta*3>^2图46 47.改一下就成为空间感更强的花曲线了;>theta = t*360r=10-<3*sin<theta*3>>^2z=<r*sin<theta*3>>^2图4748.螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos<theta>y = b*sin<theta>z=t*12图48 49.甚至这种螺旋花曲线theta = t*360*4r=10+<3*sin<theta*2.5>>^2z = t*16图49 50 鼓形线笛卡尔方程r=5+3.3*sin<t*180>+ttheta=t*360*10z=t*10图50 51 长命锁曲线笛卡尔方程：a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos<a>+rr2*cos<b>+rr3*cos<c>y=rr1*sin<a>+rr2*sin<b>+rr3*sin<c>图51 52 簪形线球坐标方程：rho=200*ttheta=900*tphi=t*90*10图52 53.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3z=t^3*<t+1>图53 54.蘑菇曲线rho=t^3+t*<t+1>theta=t*360phi=t^2*360*20*20图54 55. 8字曲线a=1b=1x=3*b*cos<t*360>+a*cos<3*t*360>Y=b*sin<t*360>+a*sin<3*t*360>图55 56.梅花曲线theta=t*360r=100+50*cos<5*theta>z=2*cos<5*theta>图56 57.桃形曲线rho=t^3+t*<t+1>theta=t*360phi=t^2*360*10*10图57 58.名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =<sin<3.5*theta-90>>+24图58 59.环形二次曲线笛卡儿方程：x=50*cos<t*360>y=50*sin<t*360>z=10*cos<t*360*8>图59 60 蝶线球坐标：rho=4*sin<t*360>+6*cos<t*360^2>theta=t*360phi=log<1+t*360>*t*360图60 61.正弦周弹簧笛卡尔：ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin<ang1>*5+cos<ang2>z=sin<ang2>Pro/E 各种曲线方程集合〔四〕62.环形螺旋线x=〔50+10*sin<t*360*15>>*cos<t*360>y=<50+10*sin<t*360*15>>*sin<t*360>z=10*cos<t*360*5>图62 63.内接弹簧x=2*cos<t*360*10>+cos<t*180*10>y=2*sin<t*360*10>+sin<t*180*10>z=t*6图63 64.多变内接式弹簧x=3*cos<t*360*8>-1.5*cos<t*480*8>y=3*sin<t*360*8>-1.5*sin<t*480*8>z=t*8图64 65.柱面正弦波线柱坐标：方程r=30theta=t*360z=5*sin<5*theta-90>图65 66. ufo 〔漩涡线〕球坐标：rho=t*20^2theta=t*log<30>*60phi=t*7200图66 67. 手把曲线thta0=t*360thta1=t*360*6r0=400r1=40r=r0+r1*cos<thta1>x=r*cos<thta0>y=r1*sin<thta1>z=0图67 68.篮子圆柱坐标r=5+0.3*sin<t*180>+ttheta=t*360*30z=t*5图68 69. 圆柱齿轮齿廓的渐开线方程：afa=60*tx=10*cos<afa>+pi*10*afa/180*sin<afa>x=10*sin<afa>-pi*10*afa/180*cos<afa>z=0注：afa为压力角,取值范围是0到60,10为基圆半径.图69 70.对数螺旋曲线柱坐标：r=sqrt<theta>theta=t*360*30z=0图70 71. 罩形线球坐标:rho=4theta=t*60phi=t*360*10图7172. 向日葵线theta=t*360r=30+10*sin<theta*30>z=0图72 73. 太阳线r=1.5*cos<50*theta>+1theta=t*360z=0图73 74 塔形螺旋线r=t*80+50theta=t*360*10z=t*80图74 75 花瓣线球坐标：rho=t*20theta=t*360*90phi=t*360*10图75 76 双元宝线r=sin<t*360*10>+30theta=sin<t*360*15>z=sin<t*3>图76 77 阿基米德螺线的变形〔自己想得〕不知前面有没有？？:what柱坐标下：theta=360*2*<t-0.5>r=10*thetaz=0图77 78 改过来的渐开线方程r=20ang = t*360x=r*cos<ang>+2*pi*r*t*sin<ang>y=r*sin<ang>-2*pi*r*t*cos<ang>z=0图78 79 双鱼曲线球坐标系rho=30+10*sin<t*360*10>theta=t*180*cos<t*360*10>phi=t*360*30图7980 蝴蝶结曲线x=200*t*sin<t*3600>y=250*t*cos<t*3600>z=300*t*sin<t*1800>图80 81 "两相望"曲线球坐标系rho=30theta=t*360*cos<t*360*20>phi=t*360*20图81 Pro/E 各种曲线方程集合〔五〕82 小蜜蜂笛卡尔坐标系：x=cos<t*360>+cos<3*t*360>Y=sin<t*360>+sin<5*t*360>图82 83 弯月x=cos<t*360>+cos<2*t*360>Y=sin<t*360>*2+sin<t*360>*2图83 84 热带鱼a=5x=<a*<cos<t*360*3>>^4>*ty=<a*<sin<t*360*3>>^4>*t图84 85 燕尾剪x=3*cos<t*360*4>y=3*sin<t*360*3>z=t图85 86 天蚕丝theta=t*3600r=<cos<360*t*20>*.5*t+1>*t图8687 心电图圆柱坐标系：r=sin<t*360*2>+.2theta=10+t*<6*360>z=t*388 变化后的星形线迪卡尔坐标系theta=t*360x=10*cos<theta>^3y=10*sin<theta>^3z=cos<theta>89 小白兔theta=t*360-90r=cos<360*<t/<1+t^<6.5>>>*6*t>*3.5+5图89 90 大家好theta=t*360+180r=cos<360*t^3*6>*2+5图90 91 蛇形线笛卡尔坐标系：x=2*cos<t*360*3>*ty=2*sin<t*360*3>*tz=<sqrt<sqrt<sqrt<t>>>>^3*5图91 92 五环柱坐标：theta=t*360*4r=cos<t*360*5>+1图92 93 蜘蛛网柱坐标：theta=t*360*5r=t*sin<t*360*25>*5+8图93 94 次声波笛卡尔:x=t*5y=t*cos<t*360*8>图94 95 十字渐开线柱坐标：theta=t*360*4r=<cos<t*360*16>*0.5*t+1>*t图95 96 内五环笛卡尔theta=t*360*4x=2+<10-5>*cos<theta>+6*cos<<10/6-1>*theta> y=2+<10-5>*sin<theta>-6*sin<<10/6-1>*theta>图96 97 蜗轨线柱坐标;theta=t*360*2r=cos<t*360*30>*t*0.5+t*2图97钣金件展开长度计算的推导在Pro/E钣金模块中,计算折弯部分的展开长度公式是：DL＝<pi/2*Ri+y_factor*t>*a/90式中：DL板材的中性层长度Ri 折弯内径y_factor Y轴比例因子T板材厚度a 折弯部分相对的圆心角以下是推导过程：其中,k为中性层系数〔即内壁到中性层距离与板厚的比值〕DL＝2＊pi〔Ri+k*T>*a/360＝<pi*Ri+pi*k*T>*a/180＝<pi/2*Ri+pi/2*k*T>*a/90令pi/2*k=y_factor则DL＝<pi/2*Ri+y_factor*T>*a/90我个人认为,其中的k因子对我们计算展开长度有直接意义,所以在设定折弯许可的时候,设定k因子就可以了.k值针对不同的材料有不同的值.普通钢板k值为0.45,实际取0.5,误差极小.关系中使用的函数数学函数下列运算符可用于关系〔包括等式和条件语句〕中.关系中也可以包括下列数学函数：cos <> 余弦tan <> 正切sin <> 正弦sqrt <> 平方根asin <> 反正弦acos <> 反余弦atan <> 反正切sinh <> 双曲线正弦cosh <> 双曲线余弦tanh <> 双曲线正切注释：所有三角函数都使用单位度.log<> 以10为底的对数ln<> 自然对数exp<> e的幂abs<> 绝对值ceil<> 不小于其值的最小整数floor<> 不超过其值的最大整数可以给函数ceil和floor加一个可选的自变量,用它指定要圆整的小数字数.带有圆整参数的这些函数的语法是：ceil<parameter_name或number, number_of_dec_places>floor <parameter_name 或 number, number_of_dec_places>其中number_of_dec_places是可选值：·可以被表示为一个数或一个使用者自定义参数.如果该参数值是一个实数,则被截尾成为一个整数.·它的最大值是8.如果超过8,则不会舍入要舍入的数〔第一个自变量〕,并使用其初值.·如果不指定它,则功能同前期版本一样.使用不指定小数部分位数的ceil和floor函数,其举例如下：ceil <10.2> 值为11floor <10.2> 值为 11使用指定小数部分位数的ceil和floor函数,其举例如下：ceil <10.255, 2> 等于10.26ceil <10.255, 0> 等于11 [ 与ceil <10.255>相同 ]floor <10.255, 1> 等于10.2floor <10.255, 2> 等于10.26曲线表计算曲线表计算使使用者能用曲线表特征,通过关系来驱动尺寸.尺寸可以是草绘器、零件或组件尺寸.格式如下：evalgraph<"graph_name", x> ,其中graph_name是曲线表的名称,x是沿曲线表x-轴的值,返回y值.对于混合特征,可以指定轨线参数trajpar作为该函数的第二个自变量.注释：曲线表特征通常是用于计算x-轴上所定义范围内x值对应的y值.当超出范围时,y值是通过外推的方法来计算的.对于小于初始值的x值,系统通过从初始点延长切线的方法计算外推值.同样,对于大于终点值的x值,系统通过将切线从终点往外延伸计算外推值.复合曲线轨道函数在关系中可以使用复合曲线的轨道参数trajpar_of_pnt.下列函数返回一个0.0和1.0之间的值：trajpar_of_pnt<"trajname", "pointname">其中trajname是复合曲线名,pointname是基准点名.轨线是一个沿复合曲线的参数,在它上面垂直于曲线切线的平面通过基准点.因此,基准点不必位于曲线上；在曲线上距基准点最近的点上计算该参数值.如果复合曲线被用作多轨道扫瞄的骨架,则trajpar_of_pnt与trajpar或1.0 - trajpar一致〔取决于为混合特征选择的起点〕.关于关系关系〔也被称为参数关系〕是使用者自定义的符号尺寸和参数之间的等式.关系捕获特征之间、参数之间或组件组件之间的设计关系,因此,允许使用者来控制对模型修改的影响作用.关系是捕获设计知识和意图的一种方式.和参数一样,它们用于驱动模型－改变关系也就改变了模型.关系可用于控制模型修改的影响作用、定义零件和组件中的尺寸值、为设计条件担当约束〔例如,指定与零件的边相关的孔的位置〕.它们用在设计过程中来描述模型或组件的不同部分之间的关系.关系可以是简单值〔例如,d1=4〕或复杂的条件分支语句.关系类型有两种类型的关系：·等式 - 使等式左边的一个参数等于右边的表达式.这种关系用于给尺寸和参数赋值.例如：简单的赋值：d1 = 4.75复杂的赋值：d5 = d2*<SQRT<d7/3.0+d4>>·比较 - 比较左边的表达式和右边的表达式.这种关系通常用于作为一个约束或用于逻辑分支的条件语句中.例如：作为约束：<d1 + d2> > <d3 + 2.5>在条件语句中；IF <d1 + 2.5> >= d7增加关系可以把关系增加到：·特征的截面〔在草绘模式中,如果最初通过选择"草绘器">"关系">"增加"来创建截面〕.·特征〔在零件或组件模式下〕.·零件〔在零件或组件模式下〕.·组件〔在组件模式下〕.当第一次选择关系菜单时,预设为查看或改变当前模型〔例如,零件模式下的一个零件〕中的关系.要获得对关系的访问,从"部件"或"组件"菜单中选择"关系",然后从"模型关系"菜单中选择下列命令之一：·组件关系 - 使用组件中的关系.如果组件包含一个或多个子组件, "组件关系"菜单出现并带有下列命令：─当前 - 缺省时是顶层组件.─名称 - 键入组件名.·骨架关系 - 使用组件中骨架模型的关系〔只对组件适用〕.·零件关系 - 使用零件中的关系.·特征关系 - 使用特征特有的关系.如果特征有一个截面,那么使用者就可选择：获得对截面〔草绘器〕中截面〔草绘器〕中关系的访问,或者获得对作为一个整体的特征中的关系的访问.·数组关系 - 使用数组所特有的关系.注释：─如果试图将截面之外的关系指派给已经由截面关系驱动的参数,则系统再生模型时给出错误信息.试图将关系指派给已经由截面之外关系驱动的参数时也同样.删除关系之一并重新生成.─如果组件试图给已经由零件或子组件关系驱动的尺寸变量指派值时,出现两个错误信息.删除关系之一并重新生成.─修改模型的单位元可使关系无效,因为它们没有随该模型缩放.有关修改单位的详细信息,请参阅"关于公制和非公制度量单位"帮助主题.关系中使用参数符号在关系中使用四种类型的参数符号：·尺寸符号 - 支持下列尺寸符号类型：─d# - 零件或组件模式下的尺寸.─d#:# - 组件模式下的尺寸.组件或组件的进程标识添加为后缀.─rd# - 零件或顶层组件中的参考尺寸.─rd#:# - 组件模式中的参考尺寸〔组件或组件的进程标识添加为后缀〕.─rsd# - 草绘器中〔截面〕的参考尺寸.─kd# - 在草绘〔截面〕中的已知尺寸〔在父零件或组件中〕.·公差 - 这些是与公差格式相关连的参数.当尺寸由数字的转向符号的时侯出项这些符号.─tp m# - 加减对称格式中的公差；#是尺寸数.─tp# - 加减格式中的正公差；#是尺寸数.─tm# - 加减格式中的负公差；#是尺寸数.·实例数 - 这些是整数参数,是数组方向上的实例个数.─p# - 其中#是实例的个数.注释：如果将实例数改变为一个非整数值,Pro/ENGINEER将截去其小数部分.例如,2.90将变为2.·使用者参数 - 这些可以是由增加参数或关系所定义的参数.例如：V olume = d0*d1*d2Vendor = "Stockton Corp."注释：─使用者参数名必须以字母开头〔如果它们要用于关系的话〕.─不能使用d#、kd#、rd#、tm#、tp#、或tpm#作为使用者参数名,因为它们是由尺寸保留使用的.─使用者参数名不能包含非字母数字字符,诸如!、、#、$.网上收集的一些曲线参数方程,和大家共享飞碟球坐标 rho=20*t^2 theta=60*log<30>*t phi=7200*t "rho=200*t" "theta=900*t" "phi=t*90*10"篮子圆柱坐标 r=5+0.3*sin<t*180>+t theta=t*360*30 z=t*5正弦曲线笛卡尔坐标系 eyf4 x=50*t y=10*sin<t*360> z=0螺旋线<Helical curve> 圆柱坐标 r=t theta=10+t*<20*360> z=t*3蝴蝶曲线球坐标 rho = 8 * t theta = 360 * t * 4 phi = -360 * t * 8Rhodonea 曲线采用笛卡尔坐标系 theta=t*360*4 x=25+<10-6>*cos<theta>+10*cos<<10/6-1>*theta> y=25+<10-6> *sin<theta>-6*sin<<10/6-1>*theta>圆内螺旋线采用柱座标系 theta=t*360 r=10+10*sin<6*theta> z=2*sin<6*theta>渐开线的方程 r=1 ang=360*t s=2*pi*r*t x0=s*cos<ang> y0=s*sin<ang> x=x0+s*sin<ang> y=y0-s*cos<ang> z=0 对数曲线 z=0 x = 10*t y = log<10*t+0.0001>球面螺旋线采用球坐标系 rho=4 theta=t*180 phi=t*360*20双弧外摆线卡迪尔坐标 l=2.5 b=2.5 x=3*b*cos<t*360>+l*cos<3*t*360> Y=3*b*sin<t*360>+l*sin<3*t*360>星行线卡迪尔坐标 a=5 x=a*<cos<t*360>>^3 y=a*<sin<t*360>>^3心臟線圓柱坐標 a=10 r=a*<1+cos<theta>> theta=t*360葉形線笛卡儿坐標 a=10 x=3*a*t/<1+<t^3>> y=3*a*<t^2>/<1+<t^3>>笛卡儿坐标下的螺旋线 x = 4 * cos < t *<5*360>> y = 4 * sin < t *<5*360>> z = 10*t抛物线 eyf13 笛卡儿坐标 x =<4 * t> y =<3 * t> + <5 * t ^2> z =0碟形弹簧eyf12圓柱坐标r =5 theta = t*3600 z =<sin<3.5*theta-90>>+24*t如何制作螺旋线〔Helical Curve〕________________________________________制作螺旋线有下列二个方法：1、formed curve ；2、利用方程式〔from equation〕________________________________________一.Formed curve：1、首先建立缺省的datum plan；并建立一个参数p,用来控制螺旋圈数〔set up/parameters/create/real parameters ,初始值可以设为：1〕2、建立圆柱体〔或者圆柱曲面〕,3、建立form curve,选择tang plane 为sketching plane,选择圆柱体的顶面为top,然后绘制如图2直线：图2注意事项：a、对齐直线的两个端点〔右上端点对齐圆柱的top面,左下端点对齐圆柱轴线和tang plane的交点〕b、建立coordinate system,并对齐直线的左下端点>4、建立relation：sd#=L*P*PI*D[L为圆柱的长度；P 为参数〔第一步建立的参数〕；D 为圆柱的直径；PI 为π]5、regenerate后你可以看到生成的helical curve<图3>了.图3二、利用方程式：1、首先建立缺省的datum plan,coordinate system<系统坐标>2、建立datum curve ,选择from equation3、选择coordinate system, 圆柱坐标〔cylindrical〕卡笛尔坐标<Cartesian>球坐标<sphereical>此时出现下列信息：/* For cylindrical coordinate system, enter parametric equation/* in terms of t <which will vary from 0 to 1> for r, theta and z/* For example: for a circle in x-y plane, centered at origin/* and radius = 4, the parametric equations will be:/* r = 4/* theta = t * 360/* z = 0/*-------------------------------------------------------------------其中螺旋线的方程式为：r = 螺旋线的最小半径+ t * <螺旋线的主要半径-螺旋线的最小半径>theta = t * <螺旋线的螺距* 360 * 引导角的度数<if any>z = 要求高度+ t在弹出的信息文文件内输入下列数值：4、存档退出后按ok5、你所建立的螺旋线如下图：.。

ProE曲线方程式大集合目录第1页：1碟形弹簧、2葉形线、3螺旋线(Helical curve)、4蝴蝶曲线和、5渐开线；第2页：6螺旋线、7对数曲线、8球面螺旋线、9双弧外摆线和、10星行线；第3页：11心脏线、12圆内螺旋线、13正弦曲线、14太阳线和、15费马曲线（有点像螺纹线）；第4页：16Talbot 曲线、17-4叶线、18Rhodonea 曲线、19抛物线和、20螺旋线；第5页：21三叶线、22外摆线、23Lissajous 曲线、24长短幅圆内旋轮线和、25长短幅圆外旋轮线；第6页：26三尖瓣线、27概率曲线、28箕舌线、29阿基米德螺线和、30对数螺线；第7页：31蔓叶线、32tan曲线、33双曲余弦、34双曲正弦和、35双曲正切；第8页：36一峰三驻点曲线、37八字曲线、38螺旋曲线、39圆和、40封闭球形环绕曲线；第9页：41柱坐标螺旋曲线、42蛇形曲线、43-8字形曲线、44椭圆曲线和、45梅花曲线；第10页：46花曲线、47空间感更强的花曲线、48螺旋上升的椭圆线、49螺旋花曲线和、50鼓形线；第11页：51长命锁曲线、52簪形线、53螺旋上升曲线、54蘑菇曲线和、55-8字曲线；第12页：56梅花曲线、57桃形曲线、58碟形弹簧、59环形二次曲线和、60蝶线；第13页：61正弦周弹簧、62环形螺旋线、63内接弹簧、64多变内接式弹簧和65、柱面正弦波线；第14页：66ufo（漩涡线）、67手把曲线、68篮子、69圆柱齿轮齿廓的渐开线方程和、70对数螺旋曲线；第15页：71罩形线、72向日葵线、73太阳线、74塔形螺旋线和、75花瓣线；第16页：76双元宝线、77阿基米德螺线的变形、78渐开线方程、79双鱼曲线和、80蝴蝶结曲线；第17页：81“两相望”曲线、82小蜜蜂、83弯月、84热带鱼和、85燕尾剪；第18页：86天蚕丝、87心电图、88变化后的星形线、89小白兔和、90大家好；第19页：91蛇形线、92五环、93蜘蛛网、94次声波和、95十字渐开线；第20页：96内五环和、97蜗轨线；1.碟形弹簧圓柱坐标方程：r = 5theta = t*3600z =(sin(3.5*theta-90))+24*t 此主题相关图片如下：1.jpg2.葉形线.笛卡儿坐標标方程：a=10x=3*a*t/(1+(t^3))y=3*a*(t^2)/(1+(t^3))此主题相关图片如下：2.jpg3.螺旋线(Helical curve)圆柱坐标（cylindrical）方程：r=ttheta=10+t*(20*360)z=t*3此主题相关图片如下：3.jpg4.蝴蝶曲线球坐标方程：rho = 8 * ttheta = 360 * t * 4phi = -360 * t * 8此主题相关图片如下：4.jpg5.渐开线采用笛卡尔坐标系方程：r=1ang=360*ts=2*pi*r*tx0=s*cos(ang)y0=s*sin(ang)x=x0+s*sin(ang)y=y0-s*cos(ang)z=0此主题相关图片如下：5.jpg6.螺旋线.笛卡儿坐标方程：x = 4 * cos ( t *(5*360)) y = 4 * sin ( t *(5*360))z = 10*t此主题相关图片如下：6.jpg7.对数曲线笛卡尔坐标系方程：z=0x = 10*ty = log(10*t+0.0001)此主题相关图片如下：7.jpg8.球面螺旋线采用球坐标系方程：rho=4theta=t*180phi=t*360*20此主题相关图片如下：8.jpg9.双弧外摆线方程：l=2.5b=2.5x=3*b*cos(t*360)+l*cos(3*t*360) Y=3*b*sin(t*360)+l*sin(3*t*360) 此主题相关图片如下：9.jpg10.星行线卡迪尔坐标方程：a=5x=a*(cos(t*360))^3y=a*(sin(t*360))^3此主题相关图片如下：10.jpg11.心脏线圓柱坐标方程：a=10r=a*(1+cos(theta))theta=t*360此主题相关图片如下：11.jpg采用柱座标系方程：theta=t*360r=10+10*sin(6*theta)z=2*sin(6*theta)此主题相关图片如下：12.jpg13.正弦曲线笛卡尔坐标系方程：x=50*ty=10*sin(t*360)z=0此主题相关图片如下：13.jpg14.太阳线（这本来是做别的曲线的，结果做错了，就变成这样了）此主题相关图片如下：14.jpg15.费马曲线（有点像螺纹线）数学方程：r＊r = a*a*theta圓柱坐标方程1: theta=360*t*5a=4r=a*sqrt(theta*180/pi)方程2: theta=360*t*5a=4由于Pro/e只能做连续的曲线，所以只能分两次做此主题相关图片如下：15.jpg16.Talbot 曲线卡笛尔坐标方程：theta=t*360a=1.1b=0.666c=sin(theta)f=1x = (a*a+f*f*c*c)*cos(theta)/ay = (a*a-2*f+f*f*c*c)*sin(theta)/b此主题相关图片如下：16.jpg17.4叶线（一个方程做的，没有复制）此主题相关图片如下：17.jpg18.Rhodonea 曲线采用笛卡尔坐标系方程：theta=t*360*4x=25+(10-6)*cos(theta)+10*cos((10/6-1)*theta) y=25+(10-6)*sin(theta)-6*sin((10/6-1)*theta)此主题相关图片如下：18.jpg19. 抛物线笛卡儿坐标方程：x =(4 * t)y =(3 * t) + (5 * t ^2)z =0此主题相关图片如下：19.jpg20.螺旋线圓柱坐标方程：r = 5theta = t*1800z =(cos(theta-90))+24*t此主题相关图片如下：20.jpg21.三叶线圆柱坐标方程：a=1theta=t*380b=sin(theta)r=a*cos(theta)*(4*b*b-1)此主题相关图片如下：21.jpg22.外摆线迪卡尔坐标方程：theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta) y=(a+b)*sin(theta)-b*sin((a/b+1)*theta) z=0此主题相关图片如下：22.jpg23. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta)此主题相关图片如下：23.jpg24.长短幅圆内旋轮线卡笛尔坐标方程：a=5b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta) y=(a-b)*sin(theta)-c*sin((a/b-1)*theta) 此主题相关图片如下：24.jpg25.长短幅圆外旋轮线卡笛尔坐标方程：theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta) y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)此主题相关图片如下：25.jpg26. 三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360)) y = a*(2*sin(t*360)-sin(2*t*360)) 此主题相关图片如下：26.jpg27.概率曲线！方程：笛卡儿坐标x = t*10-5y = exp(0-x^2)此主题相关图片如下：27.jpg28.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)此主题相关图片如下：28.jpg29.阿基米德螺线柱坐标a=100theta = t*400r = a*theta此主题相关图片如下：29.jpg30.对数螺线柱坐标theta = t*360*2.2a = 0.005r = exp(a*theta)此主题相关图片如下：30.jpg31.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x)for x此主题相关图片如下：31.jpg32.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)此主题相关图片如下：32.jpg33.双曲余弦x = 6*t-3y = (exp(x)+exp(0-x))/234.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/2此主题相关图片如下：34.jpg35.双曲正切x = 6*t-3y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x))36.一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3+1此主题相关图片如下：36.jpg37.八字曲线x = 2 * cos ( t *(2*180))y = 2 * sin ( t *(5*360))z = 0此主题相关图片如下：37.jpg38.螺旋曲线r=t*(10*180)+1theta=10+t*(20*180)z=t39.圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 0此主题相关图片如下：39.jpg40.封闭球形环绕曲线rho=2theta=360*tphi=t*360*1041.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180)) y = 100*t * sin ( t *(5*180)) z = 0此主题相关图片如下：41.jpg42.蛇形曲线x = 2 * cos ( (t+1) *(2*180)) y = 2 * sin ( t *(5*360))z = t*(t+1)43.8字形曲线柱坐标theta = t*360r=10+(8*sin(theta))^2此主题相关图片如下：43.jpg44.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)此主题相关图片如下：44.jpg45.梅花曲线柱坐标theta = t*360r=10+(3*sin(theta*2.5))^2此主题相关图片如下：45.jpg46.另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2z=4*sin(theta*3)^2此主题相关图片如下：46.jpg47.改一下就成为空间感更强的花曲线了;) theta = t*360r=10-(3*sin(theta*3))^2z=(r*sin(theta*3))^2此主题相关图片如下：47.gif48.螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*1249.甚至这种螺旋花曲线theta = t*360*4r=10+(3*sin(theta*2.5))^2z = t*16此主题相关图片如下：49.jpg50 鼓形线笛卡尔方程r=5+3.3*sin(t*180)+t theta=t*360*10z=t*1051 长命锁曲线笛卡尔方程：a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c) y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)此主题相关图片如下：51.jpg52 簪形线球坐标方程：rho=200*ttheta=900*tphi=t*90*10此主题相关图片如下：52.jpg53.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3 z=t^3*(t+1)此主题相关图片如下：53.jpg54.蘑菇曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*20*20此主题相关图片如下：54.jpg55. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360) Y=b*sin(t*360)+a*sin(3*t*360)此主题相关图片如下：55.jpg56.梅花曲线theta=t*360r=100+50*cos(5*theta)z=2*cos(5*theta)此主题相关图片如下：56.jpg57.桃形曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*10*10此主题相关图片如下：57.jpg58.名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+2459.环形二次曲线笛卡儿方程：x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)此主题相关图片如下：59.jpg60 蝶线球坐标：rho=4*sin(t*360)+6*cos(t*360^2) theta=t*360phi=log(1+t*360)*t*36061.正弦周弹簧笛卡尔：ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2)z=sin(ang2)此主题相关图片如下：61.jpg62.环形螺旋线x=（50+10*sin(t*360*15))*cos(t*360) y=(50+10*sin(t*360*15))*sin(t*360)z=10*cos(t*360*5)63.内接弹簧x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*6此主题相关图片如下：63.jpg64.多变内接式弹簧x=3*cos(t*360*8)-1.5*cos(t*480*8) y=3*sin(t*360*8)-1.5*sin(t*480*8)z=t*865.柱面正弦波线柱坐标：方程r=30theta=t*360z=5*sin(5*theta-90)此主题相关图片如下：65.jpg66. ufo （漩涡线）球坐标：rho=t*20^2theta=t*log(30)*60phi=t*720067. 手把曲线thta0=t*360thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1)x=r*cos(thta0)y=r1*sin(thta1)z=0此主题相关图片如下：67.jpg68.篮子圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*569. 圆柱齿轮齿廓的渐开线方程：afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注：afa为压力角，取值范围是0到60，10为基圆半径。