离散数学第四讲-推理规则与证明方法
- 格式:ppt
- 大小:487.00 KB
- 文档页数:20


命题逻辑的推理规则和证明方法命题逻辑是一种对简单命题和命题之间关系的形式化推理系统,广泛应用于数学、计算机科学和哲学等领域。
在命题逻辑中,推理规则和证明方法被用来推导出真实或假设的命题之间的关系。
本文将介绍命题逻辑的一些常见推理规则和证明方法。
1. 推理规则命题逻辑的推理规则是用来推导命题之间关系的规则。
以下是一些常见的推理规则:(1)析取引入规则(Disjunction Introduction Rule):如果命题P 成立,则P或Q成立。
表示为P -> (P ∨ Q)。
(2)析取消去规则(Disjunction Elimination Rule):如果P或Q 成立,且根据P和Q均能推导出命题R,则R成立。
表示为((P ∨ Q), (P -> R), (Q -> R)) -> R。
(3)合取引入规则(Conjunction Introduction Rule):如果P和Q 成立,则P且Q成立。
表示为(P, Q) -> (P ∧ Q)。
(4)合取消去规则(Conjunction Elimination Rule):如果P且Q 成立,则P和Q均成立。
表示为(P ∧ Q) -> (P, Q)。
(5)蕴含引入规则(Implication Introduction Rule):如果根据P 能推导出Q,则P蕴含Q成立。
表示为((P -> Q) -> Q) -> (P -> Q)。
(6)蕴含消去规则(Implication Elimination Rule):如果P和P蕴含Q成立,则Q成立。
表示为((P, (P -> Q)) -> Q)。
2. 证明方法证明是在命题逻辑中用于证明命题之间关系的方法。
以下是一些常见的证明方法:(1)直接证明法:假设前提命题成立,通过适当的推理规则证明出结论命题成立。
这种方法常用于证明蕴含关系。
(2)间接证明法(反证法):假设结论命题不成立,通过适当的推理规则推导出与已知事实相矛盾的命题,从而得出结论命题成立的结论。



离散数学是现代数学的一个重要分支,是计算机科学中基础理论的核心课程。
离散数学以研究离散量的结构和相互间的关系为主要目标,其研究对象一般地是有限个或可数个元素,因此他充分描述了计算机科学离散性的特点。
1、定义和定理多。
离散数学是建立在大量定义上面的逻辑推理学科。
因而对概念的理解是我们学习这门学科的核心。
在这些概念的基础上,特别要注意概念之间的联系,而描述这些联系的实体则是大量的定理和性质。
●证明等价关系:即要证明关系有自反、对称、传递的性质。
●证明偏序关系:即要证明关系有自反、反对称、传递的性质。
(特殊关系的证明就列出来两种,要证明剩下的几种只需要结合定义来进行)。
●证明满射:函数f:X Y,即要证明对于任意的y Y,都有x X,使得f(x)=y。
●证明入射:函数f:X Y,即要证明对于任意的x1、x2 X,且x1≠x2,则f(x1) ≠f(x2);或者对于任意的f(x1)=f(x2),则有x1=x2。
●证明集合等势:即证明两个集合中存在双射。
有三种情况:第一、证明两个具体的集合等势,用构造法,或者直接构造一个双射,或者构造两个集合相互间的入射;第二、已知某个集合的基数,如果为א,就设它和R之间存在双射f,然后通过f的性质推出另外的双射,因此等势;如果为א0,则设和N之间存在双射;第三、已知两个集合等势,然后再证明另外的两个集合等势,这时,先设已知的两个集合存在双射,然后根据剩下题设条件证明要证的两个集合存在双射。
●证明群:即要证明代数系统封闭、可结合、有幺元和逆元。
(同样,这一部分能够作为证明题的概念更多,要结合定义把它们全部搞透彻)。
●证明子群:虽然子群的证明定理有两个,但如果考证明子群的话,通常是第二个定理,即设<G,*>是群,S是G的非空子集,如果对于S中的任意元素a和b有a*b-1 S,则<S,*>是<G,*>的子群。


离散数学推理的三要素1.推理的形式结构(1)定义3.1:设A1,A2,A3...AK和B都是命题公式,若对于A1,A2,A3...AK和B中出现的命题变项的任意一组赋值,或者A1,A2,A3...AK为假,或者当A1,A2,A3...AK为真是,B也为真,则称由前提A1,A2,A3...AK推出结论B的推理是有效的或正确的,并称B是有效的结论。
由上面的推论可知,推理正确的并不能保证结论B一定成立,因为前提可能就不成立。
这与我们通常理解的推理是不同的。
通常只能认为在正确的前提下推出正确的结论才是正确的推理,而在这里,如果前提不正确,不论结论正确与否,都说推理正确。
(2)定理3.1:命题公式A1,A2……AK推导B的推理正确当且仅当A1,A2……AK>B为重言式。
要把推理的形式写成:前提:A1,A2……AK结论:B2自然推理系统P本节由前提A1,A2……,AK推B的正确推理的证明给出严格的形式描述。
“证明”是一个描述推理过程的命题公式序列,其中的每个公式或者是已知前提,或者是由前面的公式应用推理规则得到的结论(中间结论或推理中的结论)。
(1)定义3.2:一个形式系统I由下面4个部分组成:非空的字母表A(I);A(I)中符号构造的合式公式集E(I)E(I)中一些特殊的公式组成的公理集Ax(I)推理规则R(I)将I记为四元组<A(I),E(I),Ax(I),R(I)>.其中<A(I),E (I)>是I的形式语言系统,而<Ax(I),R(I)>为I的形式演算系统。
形式系统一般分为两类:一类是自然推理系统,它的特点是从任意给定的前提出发,应用系统中的推理规则进行推理演算,最后得到的命题公式是推理的结论(它是有效的结论,尔肯那个是重言式,也可能不是重言式)。
另一类是公理推理系统,他只能从若干条给定的公里出发,应用系统中的推理规则进行推理演算,得到的结论是系统中的重言式,成为系统中的定理。

离散数学Discrete Mathematics数理逻辑 1.5 推理规则与证明方法张晓 西北工业大学计算机学院 zhangxiao@ 2011-1-10引言什么时候数学论证是正确的? 用什么方法来构造数学论证? 数理逻辑的主要任务是用数学的方法来研究推理过 程。
所谓推理是指从前提出发推出结论的思维过程 前提是已知命题公式集合,结论是从前提出发应用 推理规则推出的命题公式。
要研究推理就应该给出推理的形式结构,为此,首 先应该明确什么样的推理是有效的或正确的。
2011-1-10离散数学21.5.1推理规则前几节所讲的命题演算, 本质上和简单的开 关代数一样, 简单的开关代数是命题演算的 一种应用。
现在, 我们从另一角度研究命题演算, 即从 逻辑推理角度来理解命题演算。
2011-1-10离散数学34个推理的例子设x属于实数, P: x是偶数, Q: x2是偶数。
例1 如果x是偶数, 则x2是偶数。
前提 x是偶数。
x2是偶数。
例2 如果x是偶数, 则x2是偶数。
x2是偶数。
2011-1-10P→Q P结论∴Q在每一例子中, 横线上的是前提, 横线下的是结论。
右侧是例子的 逻辑符表示。
P→Q Qx是偶数。
离散数学∴P4例3 如果x是偶数, 则x2是偶数。
x不是偶数。
x2不是偶数。
例4 如果x是偶数, 则x2是偶数。
x2不是偶数。
x不是偶数。
2011-1-10 离散数学P→Q P ∴ QP→Q Q ∴ P5例 1 中, 若不管命题的具体涵义, 那么它所应用的推理规则 就是 左侧规则的另一P →Q P ∴ Q种写法所对应的永真蕴 含式。
P ,P → Q 推得 QP∧(P→Q) ⇒ Q从这个永真蕴含式可看出, 它正是代表“如果 P 并且 P→Q 是真, 则 Q是 真”的意义, 这里P和Q表示任意命题。
它恰好代表左侧的推理规则。
这条推理规则叫假言推理, 从形式上看 结论Q是从P→Q中分离出来的, 所以又叫分离规则。
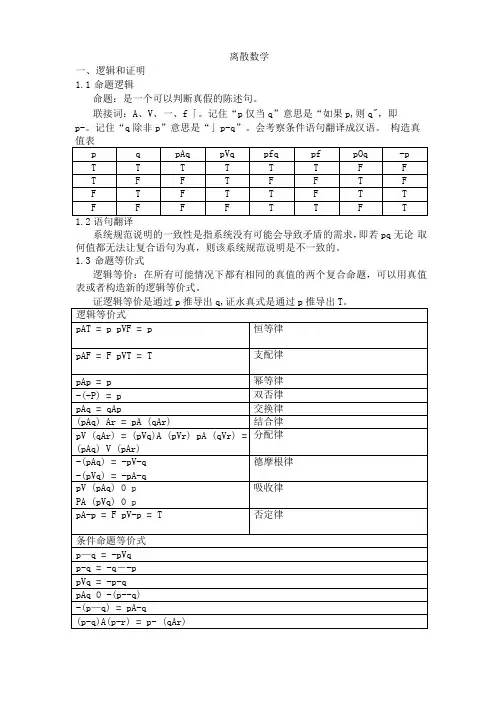
离散数学一、逻辑和证明1.1命题逻辑命题:是一个可以判断真假的陈述句。
联接词:A、V、一、f「。
记住“p仅当q”意思是“如果p,则q",即p-。
记住“q除非p”意思是“」p-q”。
会考察条件语句翻译成汉语。
构造真1.2语句翻译系统规范说明的一致性是指系统没有可能会导致矛盾的需求,即若pq无论取何值都无法让复合语句为真,则该系统规范说明是不一致的。
1.3命题等价式逻辑等价:在所有可能情况下都有相同的真值的两个复合命题,可以用真值表或者构造新的逻辑等价式。
证逻辑等价是通过p推导出q,证永真式是通过p推导出T。
(p—r)A(q-r) = (pVq)-r(p—q)V(p-r) = p—(qVr)(p—r)V(q-r) = (pAq)-r双条件命题等价式pf = (pfq) A (qfp)pf = -pfqpf Q (pAq) V(-pA-q)「(pf) = pfq1.4量词谓词+量词变成一个更详细的命题,量词要说明论域,否则没有意义,如果有约束条件就直接放在量词后面,如V x>0P(x)。
当论域中的元素可以一一列举,那么V xP(x)就等价于P(x1)AP(x2)...A P(xn)。
同理,3 xP(x)就等价于 P(x1)VP(x2)...VP(xn)。
两个语句是逻辑等价的,如果不论他们谓词是什么,也不论他们的论域是什么,他们总有相同的真值,如V x(P(x)AQ(x))和(V xP(x)) A (V xQ(x))。
量词表达式的否定:「V xP(x) Q 3 x-P(x),「3 xP(x) Q V x-P(x)。
1.5量词嵌套我们采用循环的思考方法。
量词顺序的不同会影响结果。
语句到嵌套量词语句的翻译,注意论域。
嵌套量词的否定就是连续使用德摩根定律,将否定词移入所有量词里。
1.6推理规则一个论证是有效的,如果它的所有前提为真且蕴含着结论为真。
但有效论证不代命题和量化命题的组合使用。
二、集合、函数、序列、与矩阵2.1集合£说的是元素与集合的关系,^说的是集合与集合的关系。


推理理论中的推理规则(离散数学)推理理论是一个研究推理方法与规则的学问,其中推理规则是重要的一部分。
推理规则是指在一定的条件下,由一个或多个命题出发,推出另一个命题的规则。
在离散数学中,推理规则包括一些基础的规则和一些复杂的规则。
1. 充分必要条件充分必要条件是指一个命题P能成立的充分必要条件是命题Q 成立。
即P⇔Q。
这里的充分必要条件是指两个命题是等价的,即当且仅当P成立时Q成立,Q成立时P也成立。
例如,一个三角形是等腰三角形的充分必要条件是它有两个相等的角。
2. 反证法反证法是一种常用的推理规则,它常用于证明一个命题的反命题成立。
即假设命题P不成立,通过推理得到矛盾,从而证明了P成立。
例如,证明“所有偶数都不是素数”这个命题可以采用反证法,假设有一个偶数是素数,然后推导出矛盾,从而证明“所有偶数都不是素数”。
3. 等价变形等价变形是指在推理过程中将命题变形成等价的命题。
例如,将P∧Q推导为Q∧P是一种等价变形。
等价变形可以通过逻辑符号的转换、语法规则的变换等方式实现。
4. 全称推理全称推理是指从一个全称命题出发,推出另一个全称命题。
例如,从“对于任意一个自然数n,n+1>n”这个全称命题可以推出“对于任意一个自然数m,m+2>m”。
5. 假言推理假言推理是指从一个条件命题和它的前件出发,推出它的后件的命题。
例如,从“如果今天下雨,那么他就不去逛公园。
今天不下雨”这两个命题可以推出“他会去逛公园”。
6. 假命题推理假命题推理是指从一个假命题出发进行推理,最终得到矛盾。
例如,从假设“1=2”出发,我们可以通过推导得到矛盾,并证明1不等于2。
7. 归谬法归谬法是指从前提推导出矛盾的方法,一般用于证明前提错误的情况。
例如,如果要证明“所有汉语拼音都是辅音加韵母”这个命题是错误的,可以通过归谬法证明,即找出一个汉语拼音不符合这个规则。
8. 消解法消解法是推理中常用的一种方法,可用于在两个命题中推导得到新的命题。
数理逻辑学推理与证明的规则数理逻辑学是一门关于推理和证明的学科,它涉及到符号和形式语言的运用,以及逻辑规则的应用。
在数理逻辑学中,推理和证明是重要的概念,它们是理解和应用逻辑规则的基础。
本文将介绍数理逻辑学中推理与证明的规则。
一、命题逻辑的推理规则命题逻辑是数理逻辑学中最基本的逻辑系统之一,它研究的是命题之间的逻辑关系。
在命题逻辑中,有一些重要的推理规则,以及与之对应的推理法则。
1. 求析取式的析取律对于任意两个命题p和q,根据析取律,我们可以推出以下推理规则:p ∨ q / q ∨ p这条规则表明,对于任意两个命题p和q,如果p或q为真,那么q或p也为真。
这是由于析取运算的交换律所导致的。
2. 求合取式的合取律对于任意两个命题p和q,根据合取律,我们可以推出以下推理规则:p ∧ q / q ∧ p这条规则表明,对于任意两个命题p和q,如果p和q都为真,那么q和p也为真。
这是由于合取运算的交换律所导致的。
3. 充分条件的推理规则命题p和q之间的充分条件可以表示为:p → q。
根据充分条件的定义,我们可以得到以下推理规则:p → q, p / q这条规则表明,如果p蕴含q,且p为真,那么q也为真。
这是由于充分条件的逻辑定义所导致的。
二、一阶逻辑的推理规则一阶逻辑是一种更为复杂的逻辑系统,它涉及到谓词和量词的运用。
在一阶逻辑中,也存在着一些重要的推理规则。
1. 全称量词的推理规则对于任意一个命题P(x),P(x)对于任意x都成立,根据全称量词的定义,我们可以得到以下推理规则:∀x P(x) / P(a)这条规则表明,如果对于任意x,P(x)都成立,那么可以通过实例化的方式,将全称量词中的变量替换为具体的个体,从而得到一个命题。
这是由于全称量词的逻辑定义所导致的。
2. 存在量词的推理规则对于任意一个命题P(x),存在一个x使得P(x)成立,根据存在量词的定义,我们可以得到以下推理规则:∃x P(x) / P(a)这条规则表明,如果存在一个x使得P(x)成立,那么可以通过实例化的方式,将存在量词中的变量替换为具体的个体,从而得到一个命题。
离散数学中的逻辑推理方法逻辑推理是离散数学中的重要概念,它是一种通过推理和论证来得出结论的方法。
逻辑推理在数学、计算机科学、哲学等领域都有广泛的应用。
本文将探讨离散数学中的逻辑推理方法,包括命题逻辑、谓词逻辑和推理规则。
命题逻辑是逻辑推理的基础,它研究的是命题之间的关系。
命题是陈述一个明确的陈述句,可以是真或假。
命题逻辑使用逻辑运算符来连接命题,包括合取、析取、蕴含和等价。
合取表示“且”,析取表示“或”,蕴含表示“如果...则”,等价表示“当且仅当”。
通过这些逻辑运算符,我们可以对命题进行逻辑推理。
谓词逻辑是命题逻辑的扩展,它研究的是命题中的变量和量词。
谓词逻辑引入了谓词符号和量词符号。
谓词符号表示一个命题中的属性或关系,而量词符号表示命题的范围。
谓词逻辑使用量词来限定变量的取值范围,包括全称量词和存在量词。
全称量词表示对于所有的变量都成立,存在量词表示存在一个变量成立。
通过谓词逻辑,我们可以推理出更加复杂的命题。
在逻辑推理中,我们可以使用一些推理规则来推导出新的命题。
其中最常用的推理规则有假言推理、析取三段论和拒取三段论。
假言推理是通过蕴含关系来推导新的命题。
如果我们知道一个条件蕴含另一个条件,那么我们可以推导出新的条件。
析取三段论是通过两个条件的析取来推导出一个新的条件。
拒取三段论是通过两个条件的否定来推导出一个新的条件。
这些推理规则可以帮助我们在逻辑推理中得出正确的结论。
除了推理规则,逻辑推理还涉及到一些重要的概念,如充分必要条件和等价条件。
充分必要条件是指一个条件是另一个条件的必要条件,同时另一个条件也是这个条件的充分条件。
等价条件是指两个条件互相蕴含,即一个条件成立时另一个条件也成立。
通过理解这些概念,我们可以更好地进行逻辑推理。
总之,离散数学中的逻辑推理方法是一种通过推理和论证来得出结论的方法。
命题逻辑和谓词逻辑是逻辑推理的基础,通过逻辑运算符和量词来连接和限定命题。
推理规则和重要概念如充分必要条件和等价条件可以帮助我们进行逻辑推理。
离散数学逻辑推理规则
嘿,朋友们!今天咱们来聊聊离散数学里的逻辑推理规则。
啥是离散数学的逻辑推理规则呢?简单说,就是在离散数学这个领
域里,咱们怎么根据已知的条件和信息,有理有据地推出新的结论。
先来说说允许的行为哈。
比如说,咱们可以根据给定的命题和已经
证明过的定理,一步一步地推导。
就像搭积木一样,一块一块稳稳地
往上加,只要每一步都有理有据,那就是被允许的。
再说说禁止的行为。
可千万别乱猜!不能毫无根据就得出结论,这
就像闭着眼睛走路,容易摔跟头。
也不能随便否定已经被严格证明过
的定理和规则,不然整个推理的大厦可就要摇摇欲坠啦。
举个例子哈,如果已知“所有的猫都会抓老鼠”,又知道“小花是一只猫”,那咱们就能得出“小花会抓老鼠”的结论。
这就是合理的推导。
但
要是说“因为我觉得小花长得可爱,所以它会抓老鼠”,这可就不行啦,这完全没逻辑嘛!
为啥要有这些规则呢?这就好比咱们玩游戏得有游戏规则,不然就
乱套啦。
在离散数学里,有了明确的逻辑推理规则,才能保证咱们得
出的结论是可靠的,是能站得住脚的。
而且哦,掌握好这些规则,能让咱们的思维更加清晰,解决问题更
加有条理。
就像在迷宫里有了地图,能更快找到出口。
总之呢,离散数学的逻辑推理规则很重要,咱们要遵守允许的,避开禁止的,这样才能在离散数学的世界里畅游,得出准确又靠谱的结论!好啦,希望大家都能玩转这些规则,在离散数学里玩得开心!。