热力学方程简单介绍补充

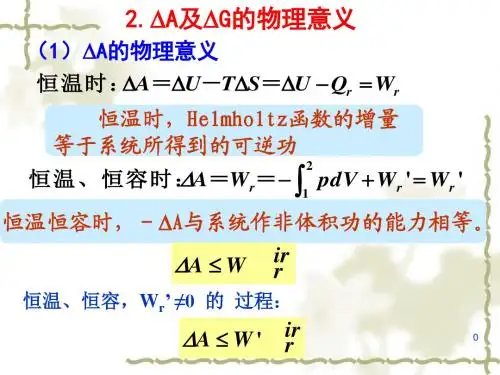
写出四个热力学基本方程
1.热力学的四个基本公式：dU=TdS-PdV；dH=TdS+VdP；
dF=-SdT-PdV；dG=-SdT+VdP。

热力学是从宏观角度研究物质的热运动性质及其规律的学科。

属于物理学的分支，它与统计物理学分别构成了热学理论的宏观和微观两个方面。

热力学定律，是描述物理学中热学规律的定律，包括热力学第零定律、热力学第一定律、热力学第二定律和热力学第三定律。

其中热力学第零定律又称为热平衡定律，这是因为热力学第一、第二定律发现后才认识到这一规律的重要性；热力学第一定律是能量守恒与转换定律在热现象中的应用；热力学第二定律有多种表述，也叫熵增加原理。

热力学第一定律也就是能量守恒定律。

自从焦耳以无以辩驳的精确实验结果证明机械能、电能、内能之间的转化满足守恒关系之后，人们就认为能量守恒定律是自然界的一个普遍的基本规律。

热力学第二定律的每一种表述，都揭示了大量分子参与的宏观过程的方向性，使人们认识到自然界中进行的涉及热现象的宏观过程都具有方向性。

2.热力学第二定律的英文解释是熵是趋向于总体增大,比如
1L90度水(A)和1L10度水(B)融合,不会是A的温度增加而 B的温度减小，因为如此的话，总体的熵减小。

如果A 温度降但B温度升高一点，其总体的熵增加。

热力学第三
定律通常表述为绝对零度时，所有纯物质的完美晶体的熵值为零。

或者绝对零度（T=0K即-273.15℃）不可达到。

R.H.否勒和 E.A.古根海姆还提出热力学第三定律的另一种表述形式：任何系统都不能通过有限的步骤使自身温度降低到0K，称为0K不能达到原理。

热力学知识：热力学中物态方程和状态方程导言：热力学是物理学中一个重要的分支，以研究物质的热现象和能源转化为主要内容。

物态方程和状态方程是其中的重要概念，作为建立热力学模型的重要工具，广泛应用于自然科学领域，特别是化学、材料科学、环境科学等领域。

本文将介绍物态方程和状态方程的概念、定义以及应用，帮助读者更加深入理解热力学基本知识。

一、物态方程的概念和定义物态方程，简称态方程，是热力学中描述物质状态的方程，它通过描述温度、压力、体积、物质的量等参数之间的关系，来表征物质的状态。

广义的物态方程可以描述固体、液体和气体的状态。

不同物质的物态方程不同，相同物质在不同环境下物态方程也不同。

下面我们逐一介绍几种常见的物态方程。

1.理想气体状态方程理想气体状态方程是描述理想气体状态的经典方程，其公式为：PV = nRT其中，P表示气体的压强，V表示气体的体积，n表示气体的物质的量，T表示气体的温度，R为普适气体常数。

这个方程表明，当方程两边保持相等的情况下，一定能够精确地描述理想气体的状态。

2.凝聚态物质状态方程凝聚态物质包括固体和液体两种状态，分别有不同的物态方程。

在热力学中，固体和液体状态的物态方程非常多，具体的方程也各自不同。

但是可以统一的是，凝聚态物质的物态方程需要考虑温度、压强、物质的密度等因素，其数学形式也更加复杂，不再是简单的线性函数关系。

3.物态方程的应用举例物态方程广泛应用于各种领域，如化学、材料科学、环境科学等。

例如在燃料电池中，物态方程可以帮助我们建立氢气氧气反应的热力学模型，以描绘反应的特性，从而满足燃料电池产生电能的需求。

再比如，在化学反应中，物态方程能够帮助我们确定气态反应物和产物的浓度，从而计算反应的进程。

二、状态方程的概念和定义状态方程是热力学的另一重要概念，通常定义为系统状态参数之间的函数关系。

与物态方程不同，状态方程是相对广义的，既可以描述单一物质的状态，也可以描述多相系物质的状态。

化学反应热力学方程解析与实验应用热力学是研究热量与能量转化的科学，而热力学方程则是描述化学反应过程中产生或吸收热量的数学表达式。

本文将解析化学反应热力学方程的基本原理，并探讨其在实验应用中的重要性。

一、热力学方程的基本原理1. 热化学方程的表示形式化学反应热力学方程一般采用如下形式表示：aA + bB → cC + dD + Q其中，a、b、c、d分别表示反应物与生成物的系数，Q表示反应过程释放或吸收的热量。

这种表示形式简洁明了，能够准确描述反应过程中的能量变化情况。

2. 热力学方程的计算在化学反应中，反应物与生成物的热化学方程式中，每个物质的系数代表其摩尔数比例。

根据热化学方程式，可以计算反应物与生成物的摩尔焓变（ΔH），即单位摩尔物质在反应过程中释放或吸收的热量。

ΔH可通过使用热量计等实验装置测量得到，也可以通过计算得出。

二、实验应用1. 反应热的测定热力学方程的应用之一是测定反应热。

通过实验控制反应物的摩尔比例，测量反应前后的温度变化，可以计算出反应的摩尔焓变（ΔH）。

这种方法被广泛应用于工业反应热的测定、燃料热值的测定等领域。

2. 化学平衡与热力学方程热力学方程对于描述化学反应平衡也起到了重要的作用。

根据热力学方程，可以计算出化学反应的标准焓变（ΔH°），并以此判断反应的热力学稳定性。

当ΔH°为负值时，反应为放热反应，有利于反应的进行；当ΔH°为正值时，反应为吸热反应，反应的进行受到限制。

3. 反应机理的解析热力学方程还可以帮助解析化学反应的机理。

通过对反应物与生成物之间的能量转化进行分析，可以揭示化学反应发生的具体过程。

这对于深入理解和控制化学反应过程具有重要意义。

4. 优化反应条件热力学方程可以用于优化化学反应的条件。

通过计算不同反应条件下的ΔH，可以确定在何种条件下反应的放热或吸热程度最大，从而确定最适宜的反应条件。

总结：化学反应热力学方程是研究化学反应热量变化的重要工具。

化学反应的热力学方程化学反应中的热力学方程是描述反应物质之间热能转化关系的数学表达式。

热力学方程可以帮助我们理解反应的热效应以及相关物质之间的能量转移。

本文将探讨化学反应的热力学方程及其应用。

一、热力学方程的基本概念热力学方程是根据反应物质之间的能量转化关系建立的数学模型，可以用来计算反应的热效应。

常见的热力学方程包括热动力学平衡方程、吉布斯自由能方程和麦克斯韦关系等。

1. 热动力学平衡方程热动力学平衡方程描述了反应的热力学平衡状态，其数学表达式为：ΔG = ΔH - TΔS其中，ΔG表示反应的自由能变化，ΔH表示反应的焓变化，T表示反应的温度，ΔS表示反应的熵变化。

2. 吉布斯自由能方程吉布斯自由能方程是描述化学反应的自由能变化的数学表达式，其数学表达式为：ΔG = ΔG° + RTlnQ其中，ΔG表示反应的自由能变化，ΔG°表示标准状态下的反应的自由能变化，R表示气体常数，T表示反应的温度，Q表示反应的反应物浓度之比。

3. 麦克斯韦关系麦克斯韦关系是描述热力学量之间的关系的数学公式。

其中，常见的麦克斯韦关系有以下几种：- 对于单一组分的系统：(∂ΔG/∂T)p = -ΔH/T^2- 对于多组分的系统：(∂ΔG/∂T)p = -ΔH/T^2 + (∂(ΔG/∂P)T)（∂ΔG/∂P)T为ΔG对压强的偏导数。

二、热力学方程的应用举例热力学方程在化学反应研究和工业应用中起着重要的作用。

下面以一些具体的实例，介绍热力学方程的应用。

1. 利用热力学方程计算反应热通过测量反应物质之间的热效应，可以计算出反应热。

例如，在燃烧反应中，通过测量产生的热量和反应物质的摩尔数，可以使用热力学方程计算出反应的热效应。

2. 优化化学反应条件热力学方程可以指导化学反应的条件优化。

通过对热力学方程的分析，可以确定最佳的温度、压力和反应物浓度等条件，以最大化反应的产率或改变反应平衡。

3. 导出其他热力学关系热力学方程还可以用来导出其他重要的热力学关系，例如吉布斯-亥姆霍兹方程、亚细亚稳态方程等。

热力学方程推导热力学是研究热与能量转化关系的学科，它揭示了自然界中能量流动和转化的规律。

热力学方程是描述物质热力学性质的基本方程，它们通过研究物质的热力学过程和性质之间的关系来描述和预测物质的行为。

本文将以简洁明了的方式，推导热力学方程。

1. 热力学第一定律热力学第一定律是关于能量守恒的基本定律。

它可以表示为：ΔU = Q - W其中，ΔU表示系统内能的变化，Q表示系统吸收的热量，W表示系统对外界所做的功。

2. 热力学第二定律热力学第二定律研究的是热能在能量转化中的特性，它将能量转化的方向和过程的可逆性联系起来，提出了熵增原理。

根据热力学第二定律，熵的变化可表达为：ΔS = Q/T其中，ΔS表示系统熵的变化，Q表示系统吸收的热量，T表示系统温度。

3. 热力学方程根据热力学定律，我们可以将热力学方程表示为：dU = T dS - P dV其中，dU表示系统内能的微小变化，T表示系统温度，dS表示系统熵的微小变化，P表示系统压强，dV表示系统体积的微小变化。

通过对上述方程的推导，我们可以得到热力学方程的一般形式。

4. 理想气体的热力学方程对于理想气体，我们可以根据气体状态方程，将熵的微小变化dS 表示为：dS = C_v dT/T + R dV/V其中，C_v表示气体的定容热容，R表示气体的气体常数。

将上述表达式代入热力学方程，我们可以得到理想气体的热力学方程：dU = T (C_v dT/T + R dV/V) - P dV整理后可得：dU = C_v dT + R/T dV - P dV5. 热力学方程的应用热力学方程是研究物质的热力学性质和行为的基本工具，它可以应用于各种物理和化学过程的分析和计算。

例如，在理想气体的等温过程中，我们可以根据热力学方程来计算系统内能的变化和所做的功。

在等容过程中，我们可以利用热力学方程推导出热容的表达式。

在等压过程中，我们可以根据热力学方程来计算系统内部能量和熵的变化。

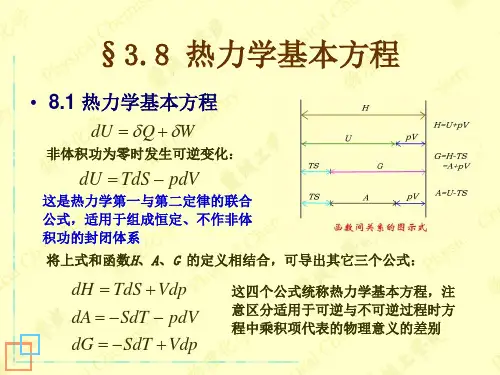
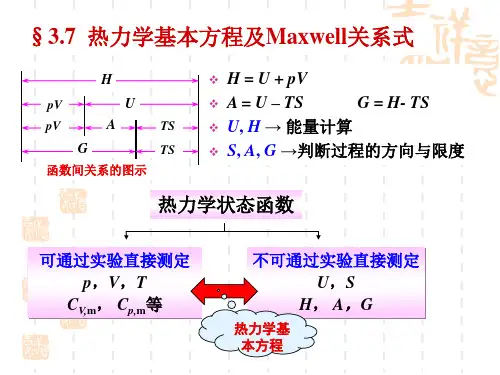
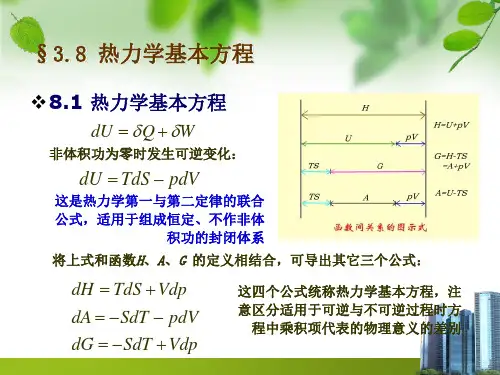
.1热力学基本方程 (Master equations of thermodynamics) 1、热力学函数定义式 H=U+PV F=U-TS G=H-TS这些函数之间的相对大小见右图。

2、特征微分方程对于定组成均相封闭系统（W ′=0），热一律dU=δQ-PdV , TdS-δQ ≥0,两律合并：dU ≤TdS-PdV.若为可逆过程，则dU=TdS-PdV (7.1)∵H=U+PV ，微分得：dH=dU+pdV+Vdp,将（7.1）式代入：dH=TdS-pdV+pdV+Vdp=TdS+Vdp(7.2) ∵F=U-TS ，微分得：dF=dU-TdS-SdT,将(7.1)式代入：dF=TdS-pdV-TdS-SdT=-SdT-pdV(7.3) ∵G=H-TS ，微分得：dG=dH-TdS-SdT ，将（7.2）式代入：dG=TdS+Vdp-TdS-SdT=-SdT+Vdp(7.4) 上述4式虽在可逆条件导出，但因涉及的均为状态函数，其改变量只与始、终态有关，而与过程是否可逆无关。

但应注意：（1）对有相变、化变的多组分多相体系不适应。

（2）在不可逆过程中，δQ R ≠TdS 及δW 体≠-pdV 。

上述4个基本方程式可见，U 、H 、F 、G 都只是两个独立变量的函数。

如U 可写为U=U （S,V ），又如G=G （T ，P ）。

即U 是S 、V 为独立变量的函数，G 是T 、P 的函数。

而U 、G 在这些独立变量作为限制条件下，其改变值可作为过程自发方向和限度的判据（但在其他变量下的改变量不能作判据）故U 相对于S 、V 变量为特征函数，G 相对于T 、P 亦是。

由此上述4式又称为特征微分方程。

6.2对应系数关系式将4个特征函数写成各自独立变量的全微分式，再与4个特征微分方程相比较，便可得出4对对应关系式。

1.关于U ：∵U=U （S 、V ），dU=dv V U ds S U sv ⎪⎭⎫⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂与dU=TdS-PdV 比较得：p V U T S U sv -=⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂, 2.关于H ：∵H=H （S ，P ），dH=dp P H ds S H sp ⎪⎭⎫⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂,与dH=TdS+VdP 比较：V P H T S H sp=⎪⎭⎫⎝⎛∂∂=⎪⎭⎫⎝⎛∂∂,。