青岛版九年级上册数学《解直角三角形》
- 格式:doc
- 大小:180.00 KB
- 文档页数:6





解直角三角形-青岛版九年级数学上册教案
一、教学目标
1.了解直角三角形的基本概念和定理;
2.掌握利用三角函数(正弦、余弦、正切)求解直角三角形的方法;
3.解决直角三角形的实际问题。
二、教学重难点
1.理解三角函数的概念和性质;
2.掌握求解应用题的方法。
三、教学内容和学生活动
1. 直角三角形的定义
学生通过PPT介绍、教师讲解及类比了解直角三角形是什么,并掌握直角三
角形的性质和基本概念;
•定义:一个三角形的其中一个角是90度,则称这个三角形为直角三角形;
•性质:直角三角形的对边为斜边,斜边的两个端点为直角和对角。
•基本概念:斜边、底边、高、角度符号等。
2. 特殊角的三角函数值
学生可以通过PPT演示、动画、练习等方式重点掌握以下角度的三角函数值:0度、30度、45度、60度、90度。
3. 三角函数的概念
•定义:在直角三角形中,正弦值、余弦值、正切值是一个角的三角比,分别表示为sin、cos、tan。
•性质:三角函数值的范围与特点。
4. 三角函数的计算方法
学生通过举例、练习等方式,使用计算器和三角函数表,掌握三角函数的计算方法。
5. 应用题例解
教师通过例题解析的方式,帮助学生理解掌握直角三角形应用题的解法,以确保学生可以应用所学知识解决实际问题。
四、教学方法
1.讲述
2.PPT演示
3.线上互动练习
五、学习评价
1.课堂小测验;
2.作业练习;
3.课后测试。
六、教学后记
通过互动形式将知识点梳理完整并同步,结合实际应用情景,丰富教学方式,激发学生的学习兴趣,提高教学效果。




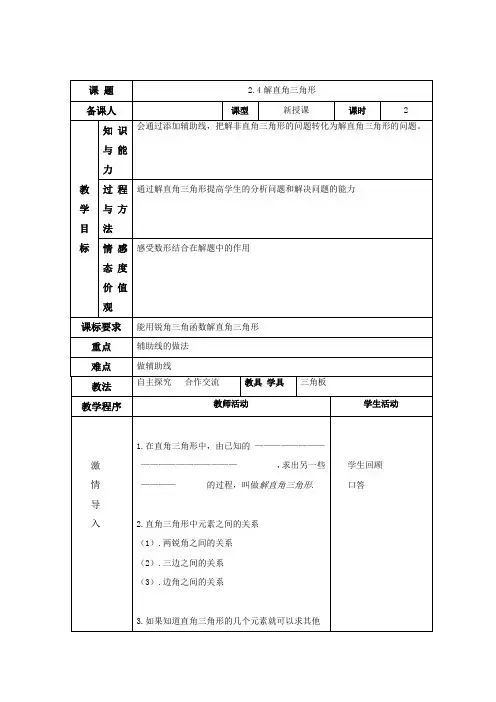
课题 2.4解直角三角形备课人课型新授课课时 2教学目标知识与能力会通过添加辅助线,把解非直角三角形的问题转化为解直角三角形的问题。
过程与方法通过解直角三角形提高学生的分析问题和解决问题的能力情感态度价值观感受数形结合在解题中的作用课标要求能用锐角三角函数解直角三角形重点辅助线的做法难点做辅助线教法自主探究合作交流教具学具三角板教学程序教师活动学生活动激情导入1.在直角三角形中,由已知的———————————————————,求出另一些————的过程,叫做解直角三角形.2.直角三角形中元素之间的关系(1).两锐角之间的关系(2).三边之间的关系(3).边角之间的关系3.如果知道直角三角形的几个元素就可以求其他学生回顾口答认定目标自主探究的元素?有几种情况?出示学习目标自学导航1、求下列各直角三角形中字母的值2、例1在△ABC中,已知∠A﹦60°,∠B﹦45°,AC﹦20厘米,求AB 的长思考(1)、∆ABC不是直角三角形怎么办?(2)、如果转化成直角三角形过那个顶点做垂线可以解决问题?3、例2、△ABC中,∠A=30°,∠ABC=135°,BC=2,求AC的长?思考(1)、∆ABC如何在不改变已知角的情况下转一生口述目标,其余生静听、领会快速利用解直角三角形的方法解决1题思考探究2、3中如何解决试写出解答过程标出困惑之处组内交流自学导航中(第5题)激情互动拓展应用化成直角三角形?指导生互动交流,解决生自学中的困惑问题点评:1、把解非直角三角形的问题转化为解直角三角形时添加辅助线一般保持原量不变。
1、自学导航2题2、自学导航3题3、课本52页练习1、2题的困惑问题,全组达成一致意见。
有困惑的组由科代表提出本组困惑问题,寻求其他组帮助,各组选派代表说明如何把解非直角三角形的问题转化为解直角三角形、添加辅助线的依据是什么?师生互动1题3号生板演完成2题2号生板演完成1号生点评、互改各组针对出现问题讨论、分析1题5号生板演完成2题4号生板演完成小结:指导生小结课堂作业互动53页3题1号生点评、互改各组针对出现问题讨论、分析生回顾浅谈收获学生当堂完成板书设计课题 2.4 解直角三角形(2)例题1例题2练习板演板演板演教学反思知识较复杂,学生运用知识解决问题是不知如何下手,特别是辅助线的作法,不知从哪个顶点作高,应加强这方面的练习。

《解直角三角形》(第1课时)教案 探究版
教学目标 知识与技能
1.掌握直角三角形中角与角(两锐角互余)、边与边(勾股定理)、角与边(锐角三角比)之间的关系.
2.已知直角三角形的两个元素(至少一个是边),会解直角三角形. 过程与方法
通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角比解直角三角形,逐步培养学生分析问题、解决问题的能力.
情感与态度
渗透数形结合的数学思想,培养学生综合运用知识的能力和良好的学习习惯. 教学重点
直角三角形的解法. 教学难点
锐角三角比在解直角三角形中的灵活运用. 教学过程 一、情景导入 教师用多媒体出示:
如图,在Rt △ABC 中,∠C =90°,
C
B
A
(1)若AC =h ,BC =l ,你能求出AB 及∠B 吗? (2)若AC =h ,∠B =α,你能求出AB 及BC 吗?
师生活动:师出示问题后,让学生分组讨论尝试求解. 师在学生充分讨论后,给出结论: (1)AB
sin ∠B
=AC
AB
=再利用计算器即可求出∠B ;
(2)AB =
sin sin AC h αα=,BC =tan tan AC h
αα
=
.
设计意图:通过具体的问题,引发学生解直角三角形的思考,为引出本节课的内容做好铺垫.
二、探究新知 观察与思考
(1)在Rt △ABC 中(如图所示),∠C =90°,∠A ,∠B ,∠C 的对边分别是a ,b ,c .除直角C 已知外,你会用含有这些字母的等式把其他5个元素之间的关系表示出来吗?与同学交流.
c a C
B A
师生活动:教师引导学生观察示意图,启发学生利用三角比的知识把除∠C 之外的5个元素之间的关系表示出来.最后把学生说出的等式按“角”、“边”、“角与边”加以分类,并进行总结.
师总结如下:
①角之间的关系:∠A +∠B =90°; ②边之间的关系:222a b c +=; ③角与边之间的关系:sin A =
a c ,cos A =
b
c ,tan A =a
b
. (2)观察上面的三组等式,你发现在直角三角形中,除直角以外,至少知道几个元素就可以求出其他的未知元素?
师生活动:教师应引导学生通过思考和交流,理解在直角三角形中,除直角外知道其中的两个元素(至少一个是边),就可以求出其他三个未知元素,由此引出解直角三角形的概念.
在讲解“除直角外知道其中的两个元素(至少一个是边),就可以求出其他三个未知元素”时师可让学生仔细观察②③两组等式,并重点讲解:
(1)在②③两组等式中,每个等式中都含有三个量.如果已知其中的两个量,则第三个量可由相应的等式求出,其中②中,三个量都是边,③中的三个量有一个是角,另外两个是边,因而在已知的两个元素中,至少有一个元素是边.“至少有一个”的含义是或者其中一个元素是边,或者两个元素都是边,因此,解直角三角形问题可分为两类:已知两边(两
条直角边或一直角边和斜边)解直角三角形,已知一边一锐角(一直角边和对角、一直角边和邻角、斜边和一锐角)解直角三角形.
(2)解直角三角形两类问题的理论依据:
已知直角三角形两边,根据基本事实“边角边”及“HL”定理,直角三角形被唯一确定,故它的未知元素可求;
已知直角三角形一边和一锐角,根据基本事实“角边角”或“角角边”定理,直角三角形也被唯一确定,故它的未知元素可求.
师在学生总结的基础上给出解直角三角形的定义:
由直角三角形中已知的元素求出未知元素的过程,叫做解直角三角形.
设计意图:通过学生的分组讨论和尝试,提高学生分析问题、归纳结论的能力,为后面的例题讲解做好理论上的铺垫.
三、例题精讲
例1 在Rt△ABC中,已知∠C=90°,a=17.5,c=62.5.解这个直角三角形.
师生活动:师可以让学生独立分析问题,在学生分析的基础上引导学生采用多种方法解决此例.
解:方法1 因为a2+b2=c2,所以60
b=.
由sin A=
17.5
62.5
a
c
==0.28,得∠A≈16°15′37″.
所以∠B=90°-∠A=90°-16°15′37″=73°44′23″.
方法2因为a2+b2=c2,所以60
b=.
由tan A=
17.5
60
a
b
=≈0.29,得∠A≈16°15′37″.
所以∠B=90°-∠A=90°-16°15′37″=73°44′23″.
方法3因为a2+b2=c2,所以60
b=.
由sin B=
60
62.5
b
c
==0.96,得∠B≈73°44′23″.
所以∠A=90°-∠B=90°-73°44′23″=16°15′37″.
设计意图:例1是已知直角三角形的两边解直角三角形的问题.解决的方法有很多,通过本例使学生明确解直角三角形时方法的多样性,培养了学生开放性思维的能力.例2 在Rt△ABC中,已知∠C=90°,c=128,∠B=52°.解这个直角三角形(边长精确到0.01).
师生活动:(1)本例是已知直角三角形的一边和一锐角解直角三角形的问题.在本例的基础上,师可以进一步提出问题“如果已知直角三角形的一条直角边和一个锐角,如何解直角三角形?”在此基础上,师引导学生归纳出解直角三角形的通法.
(2)通过本例,师引导学生探求出选择边角关系解直角三角形的两条原则:一是应当选择直接应用题目中已知条件的等式;二是应当尽量选择便于计算的等式.为此应让学生熟
悉直角三角形中边角关系式的变形,如由sin A=a
c
,变形为a=c•sin A,c=
sin
a
A
等.
解:在Rt△ABC中,由∠C=90°,∠B=52°,得∠A=90°-52°=38°.
由sin B=b
c
,得b=c•sin B=128•sin52°≈100.87;
由cos B=a
c
,得a=c•cos B=128•cos52°≈78.80.
规律方法解直角三角形的类型和解法
角形的不同类型和相应的解法,为后面的学习做好铺垫.
四、课堂练习
1.在Rt△ABC中,∠C=90°,∠A=30°,c=2,则a=______,b=_______.
2.在Rt△ABC中,∠C=90°,c=2,b=1,则a=_______,∠B=______.
3.在Rt△ABC中,∠C=90°.
(1)已知c=39,b=36,求a和∠B(精确到1′);
(2)已知a=22.5,b=12,求∠A和∠B(精确到1′).
4.在Rt△ABC中,已知∠C=90°,a=12,b=24,解这个直角三角形.
5.在Rt△ABC中,∠C=90°.
(1)已知c=15,∠B=60°,求a;
(2)已知∠A=35°,a=24,求b,c.
参考答案:
1.1
230°.
3.(1)a=15,∠B≈67°23′;
(2)∠A≈61°56′,∠B≈28°4′.
4.c=A≈26°33′54″,∠B≈63°26′6″.
5.(1)7.5;(2)b≈34.28;c≈41.84.
设计意图:通过练习熟悉解直角三角形的不同类型,巩固解不同类型直角三角形的方法.
五、课堂小结
1.理解直角三角形中角与角、边与边、角与边之间的关系.
2.知道什么是解直角三角形.
3.会区别解直角三角形的不同类型,并会选用相应的方法解直角三角形.
设计意图:通过课题小结,使学生加深对解直角三角形的理解,增强学生学习的目标性,增强学生解直角三角形的能力.
六、目标检测:
1.在△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,则有().A.tan
=⋅D.sin
c a A
=⋅
b a A
a c B
=⋅C.cos
=⋅B.sin
b c A
2.在Rt△ABC中,∠C=90°,∠B=60°,a=4,则b=______,c=_______.
3.在△ABC中,∠C=90°,试根据下表中给出的两个数值,填出其他元素的值:
4.在Rt△ABC中,已知∠C=90°,根据下列条件,解直角三角形:
(1)AC BC
(2)∠A=22.5°,b=12.
5.如图,已知直角梯形ABCD中,AD∥BC,∠D=90°,∠B=30°,CD
CA⊥AB,求AD和BC的长度.
参考答案:
1.C.
2.8.
3.(1)2,,30°;(2)3,,45°;(3)10,60°,30°;(4)6,45°,45°.
4.(1)AB=A=60°,∠B=30°;
(2)∠B=67.5°,a≈4.97,c≈12.99.
5.AD=9,BC=36.
设计意图:通过练习进一步巩固解直角三角形的能力.。