自由度(原理)

机械原理机构自由度计算要计算机械原理机构的自由度，首先需要确定机构中的连杆和连接关系。

连杆是构成机构的杆件，连接关系是将连杆连接在一起的方式。

机构中的连杆可以是刚性的或柔性的，连接关系可以通过铰链、滑动副或传动副来实现。

在计算自由度时，通常会假设连杆是刚性的，以简化计算。

计算机械原理机构的自由度时，有两种常见的方法可供选择：迭代法和非迭代法。

在迭代法中，我们首先假设机构的自由度为零，并逐步增加约束，直到无法增加为止。

每次增加约束时，我们需要检查相应的自由度是否减少。

如果自由度减少，则保留该约束；如果自由度没有减少，则将该约束排除。

通过迭代这一过程，我们最终可以得到机构的自由度。

相比之下，非迭代法更为直接。

我们可以根据机构中的约束条件和自由关系，直接计算出机构的自由度。

这种方法在约束较少或机构较简单的情况下尤其适用。

无论使用哪种方法，计算机械原理机构的自由度都需要考虑以下几个因素：1.连杆的数量：连杆的数量对机构的自由度有直接影响。

一个机构中的连杆数量越多，其自由度也就越高。

2.连杆的长度：连杆的长度决定了机构的运动幅度。

较长的连杆通常会增加机构的自由度。

3.连接关系：不同的连接关系会导致机构自由度的不同。

例如，一个通过滑动副连接的机构可能具有比通过传动副连接的机构更大的自由度。

通过对上述因素进行综合考虑，我们可以计算出机械原理机构的自由度，并据此来分析和优化机构的设计。

机构的自由度不仅与其运动性能和稳定性有关，还与动力学和控制系统的设计密切相关。

总结起来，机械原理机构的自由度计算是理解和设计复杂机构的重要步骤之一、通过迭代法或非迭代法，我们可以计算出机构的自由度，并据此分析和优化机构的性能。

在进行自由度计算时，我们需要考虑连杆的数量、长度和连接关系等因素。

这些计算为机构的设计和应用提供了理论依据。

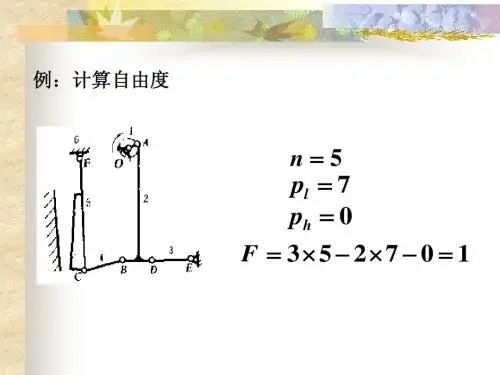
机构自由度的概念
机构自由度（Degree of Freedom, DoF）是机械原理中的一个核心概念，它描述了一个机构在没有外力或驱动力作用下能够独立完成的运动的数量。

具体来说：
机构自由度定义：
在一个机械机构中，为了确定该机构所有构件的相对位置和姿态，所需要的独立运动参数的数量称为机构的自由度。

- 对于单个构件而言，在三维空间中，它有6个自由度，包括沿三个正交方向（X、Y、Z轴）的平动自由度以及绕这三个轴的转动自由度。

- 当多个构件通过运动副（如铰链、滑块等）相互连接组成机构时，由于运动副对构件的约束作用，实际的机构自由度会小于各个独立构件自由度之和。

- 机构的总自由度计算公式为：总自由度= 各构件自由度之和- 约束数（即由运动副引入的约束数目）。

- 在实际应用中，如果机构具有一个或多个原动件（例如电机、气缸等驱动部件），并且原动件提供的独立输入变量与机构自由度相
匹配，则机构可以实现确定的、预设的运动。

平面机构自由度通常指机构在二维平面内的自由度，一般包括沿两个正交方向的移动自由度及一个绕垂直于平面轴的转动自由度。

总结来说，机构自由度是评价机构运动特性的重要指标，对于设计和分析机械设备有着至关重要的意义。

只有当机构的自由度等于零时，机构才是完全刚性固定的结构；而具有至少一个自由度的机构才能够产生相对运动，并可能成为有用的机械装置。

机械原理楔块机构自由度机械原理中的楔块机构是一种常见的机械传动装置，它利用楔形物体的力学原理实现力的放大和传递。

楔块机构的自由度是指其可自由运动的独立方向的数量。

在本文中，将详细介绍楔块机构的自由度及其影响因素。

楔块机构的自由度取决于其结构组成和约束条件。

一般来说，楔块机构由两个楔块和一个被楔块夹持的工件构成。

楔块机构的自由度可以分为平动自由度和旋转自由度两种。

我们来看楔块机构的平动自由度。

平动自由度是指楔块机构中楔块沿某一方向的自由移动能力。

通常情况下，楔块机构的平动自由度为1，即只能沿一个方向自由移动。

这是因为楔块机构的设计初衷就是为了实现工件的夹持和固定，所以只需要在一个方向上进行平动即可满足需求。

我们来看楔块机构的旋转自由度。

旋转自由度是指楔块机构中楔块绕某一轴线进行旋转的自由程度。

楔块机构的旋转自由度一般为0，也就是说楔块不能绕轴线旋转。

这是由于楔块机构的设计原理决定的，楔块的形状和夹持工件的方式使得其无法进行旋转。

楔块机构的自由度受到几个因素的影响。

首先是楔块的形状。

楔块的形状决定了其在工件夹持过程中的力学特性，从而影响了楔块机构的自由度。

其次是楔块的材料和表面处理状态。

楔块的材料和表面处理状态会影响楔块与工件之间的摩擦特性，进而影响楔块机构的自由度。

最后是楔块机构的工作环境和工况。

不同的工作环境和工况会对楔块机构的自由度造成一定影响，比如温度变化、润滑条件等。

总结起来，楔块机构的自由度是指其可自由运动的独立方向的数量，通常情况下平动自由度为1，旋转自由度为0。

楔块机构的自由度受到楔块的形状、材料和表面处理状态以及工作环境和工况等因素的影响。

了解楔块机构的自由度对于设计和应用具有重要意义，可以提高其性能和效率。

机械原理楔块机构自由度机械原理是研究机械结构和机械运动规律的一门学科，而楔块机构是其中的一种重要的机械原理。

楔块机构是利用楔形零件的变形特性来完成力的传递、定位和固定的机构。

本文将从楔块机构的自由度角度出发，探讨楔块机构的原理和应用。

我们来了解一下楔块机构的自由度。

自由度是指机构中独立运动的最小数目。

对于楔块机构来说，由于楔块的特殊形状和运动特性，其自由度是固定的，即为零。

这是因为楔块只能做直线运动，无法产生旋转运动。

因此，楔块机构在设计和应用时需要考虑其特殊的运动规律和力的传递方式。

楔块机构的主要特点之一是力的传递。

楔块机构通过楔形零件的变形来实现力的传递。

当外界施加力或载荷时，楔形零件会受到压力，从而发生变形。

利用楔形零件的变形特性，可以将外界施加的力传递给其他部件，实现力的定位和固定。

楔块机构广泛应用于各种工程领域，如夹具、刀具、锁紧装置等。

楔块机构的运动规律也是其重要的特点之一。

楔块机构的运动规律可以简单地描述为平移运动。

楔形零件在运动过程中只能沿着一条直线进行平移，不能产生旋转运动。

这种特殊的运动规律使得楔块机构在一些特殊的应用场景中具有独特的优势。

例如，在夹具中，楔块机构可以实现对工件的紧固和定位，确保工件在加工过程中的稳定性和精度。

楔块机构还具有结构简单、工作可靠等特点。

由于楔块机构的运动自由度为零，其结构相对简单，易于制造和维护。

同时，楔块机构的工作可靠性也较高，能够承受较大的载荷和变形，保证力的传递的稳定性和可靠性。

在实际应用中，楔块机构有着广泛的应用。

例如，在汽车制造中，楔块机构常用于发动机的曲轴和连杆的连接，实现动力传递；在建筑工程中，楔块机构常用于起重机的塔臂和基座的连接，确保起重机的稳定性；在工业生产中，楔块机构常用于夹具的设计，实现工件的夹紧和定位。

可以说，楔块机构在各个领域中都发挥着重要的作用。

楔块机构是一种重要的机械原理，其自由度为零。

楔块机构通过楔形零件的变形特性来实现力的传递、定位和固定。

机械原理自由度的定义The definition of degrees of freedom in mechanical principles deals with the number of independent movements a system has. 机械原理中对自由度的定义涉及系统具有的独立运动数量。

It is a critical conceptin understanding the behavior and constraints of mechanical systems. 这是理解机械系统行为和约束的重要概念。

Degrees of freedom can be understood as the number of parameters required to uniquely define the configuration of a mechanical system. 自由度可以理解为唯一定义机械系统配置所需的参数数量。

It is essential in design, analysis, and control of mechanical systems in various engineering fields. 在各种工程领域的机械系统的设计、分析和控制中至关重要。

Understanding degrees of freedom is crucial for engineers and researchers to optimize the performance and efficiency of mechanical systems. 理解自由度对于工程师和研究人员来说至关重要，以优化机械系统的性能和效率。

In mechanical systems, degrees of freedom are categorized as translational and rotational. 在机械系统中，自由度被归类为平移和旋转。