下载文档原格式
数据处理与实验设计考试卷一、单选题（每题3分，共30分）1. 在数据处理中，以下哪种统计量可以反映数据的集中趋势？（）A. 方差。
B. 标准差。
C. 平均数。
D. 极差。
2. 对于一组数据12，15，18，20，25，其中位数是（）。
A. 18.B. 19.C. 20.D. 15.3. 在实验设计中，以下哪种设计可以同时研究多个因素对实验结果的影响？（）A. 完全随机设计。
B. 随机区组设计。
C. 析因设计。
D. 拉丁方设计。
4. 当我们想要检验两个总体均值是否相等时，通常使用（）。
A. t检验。
B. F检验。
C. 卡方检验。
D. 秩和检验。
5. 在数据收集过程中，如果样本存在偏差，可能会导致（）。
A. 结果的准确性提高。
B. 结果的可靠性降低。
C. 结果不受影响。
D. 实验更容易进行。
6. 数据的离散程度可以用（）来衡量。
A. 众数。
B. 中位数。
C. 方差。
D. 平均数。
7. 在实验设计中，控制组的作用是（）。
A. 作为实验处理的对象。
B. 与实验组进行对比，排除无关因素的影响。
C. 增加实验的样本量。
D. 确定实验的变量。
8. 以下关于标准差的说法正确的是（）。
A. 标准差越大，数据越集中。
B. 标准差越小，数据越分散。
C. 标准差是方差的平方根。
D. 标准差与数据的集中趋势无关。
9. 若要研究施肥量和灌溉量对农作物产量的影响，最合适的实验设计是（）。
A. 单因素实验设计。
B. 双因素实验设计。
C. 多因素实验设计。
D. 重复测量设计。
10. 在进行数据分组时，分组的组数一般（）。
A. 越多越好。
B. 越少越好。
C. 根据数据的特点和研究目的确定。
D. 固定为5组。
二、多选题（每题5分，共25分）1. 以下属于数据处理步骤的有（）。
A. 数据收集。
B. 数据整理。
C. 数据分析。
D. 数据解释。
E. 数据删除。
2. 在实验设计中，影响实验结果的因素包括（）。
A. 自变量。
B. 因变量。
C. 控制变量。
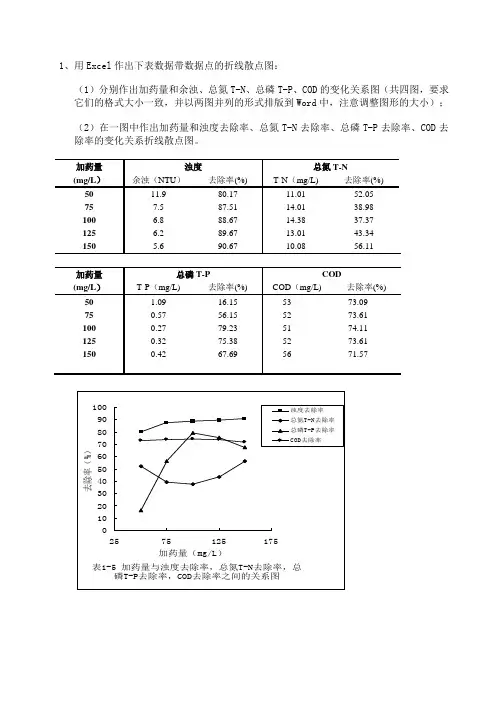
1、用Excel作出下表数据带数据点的折线散点图：（1）分别作出加药量和余浊、总氮T-N、总磷T-P、COD的变化关系图（共四图，要求它们的格式大小一致，并以两图并列的形式排版到Word中，注意调整图形的大小）；（2）在一图中作出加药量和浊度去除率、总氮T-N去除率、总磷T-P去除率、COD去除率的变化关系折线散点图。
2、对离心泵性能进行测试的实验中，得到流量Q v 、压头H 和效率η的数据如表所示，绘制离心泵特性曲线。
将扬程曲线和效率曲线均拟合成多项式。
（要求作双Y 轴图）流量Qv 、压头H 和效率η的关系数据序号1 2 3 4 5 6 Q v (m 3/h ) H/m 0.0 15.00 0.4 14.84 0.8 14.56 1.2 14.33 1.6 13.96 2.0 13.65 η0.00.0850.1560.2240.2770.333序号7 8 9 10 11 12Q v(m3/h)H/m η2.413.280.3852.812.810.4163.212.450.4463.611.980.4684.011.300.4694.410.530.4313、用荧光法测定阿司匹林中的水酸（SA），测得的工作曲线和样品溶液的数据如下表:C(SA)/μg.mL-10.50 1.00 1.50 2.00 3.00 样品1 样品2F(荧光强度) 10.9 22.3 33.1 43.5 65.4 38.2 39.2（1）列出一元线性回归方程，求出相关系数，并给出回归方程的精度；（2）求出未知液（样品）的水酸（SA）浓度。
(1)C(SA)/μg.mL-10.50 1.00 1.50 2.00 3.00 1.75 1.80F(荧光强度) 10.9 22.3 33.1 43.5 65.4 38.2 39.2(2)4、对某矿中的13个相邻矿点的某种伴生金属含量进行测定，得到如下一组数据：矿样点距离x 含量c 矿样点距离x 矿样点1 2 106.42 8 11 110.592 3 108.20 9 14 110.603 4 109.58 10 15 110.904 5 109.50 11 16 110.765 7 110.00 12 18 110.006 8 109.93 13 19 111.207 10 110.49试找出某伴生金属c与含量距离x之间的关系(要求有分析过程、计算表格以及回归图形)。
部分习题答案习题三1、62621086.6S 104.1ˆ002.74ˆ--⨯=⨯=σ=μ2、λ的极大似然估计和矩估计量均为x =λˆ 3、5、 6、（1）（5.608, 6.392） (2)(5.558, 6.442) 7、（1）（6.675, 6.681）, (6.8×10-6, 6.8×10-5) （2）(6.61, 6.667), (3.8×10-6, 5.06×10-5) 8、σ已知6.239；σ未知6.356 9、4.052610、接受H O 11、认为不合格 12、认为显著大于10 13、拒绝H O 19、接受H O习题四1、差异显著；2、只有浓度的影响是显著的.习题五1、 填料A 用量范围可能选低了.2、培烧温度与三氧化铝两个因素用量范围可能偏低.习题六1、（2）xy5503.129584.13ˆ+= （4）（11.82，13.28）（5）(19.66，20.18) 2、xy05886.06287.24ˆ+= 3、（2）)17.14,29.13)(3(,988.0104.0ˆx y+-=4、x0867318.0e 4556.32y ˆ-=5、2020381.00086.10333.19ˆx x y-+= 6、（1）31321x15.1x 575.09.9yˆ)2(x 15.1x 55.0x 575.09.9yˆ++=+++=习题七1、218.079.1419.300ˆz z y+-= 2、)1(21-=n c 212211,n n n b n n n a +=+=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛-+-⎪⎭⎫⎝⎛-+⨯+⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫⎝⎛++⎪⎭⎫⎝⎛-++=-625.1589625.1102879.11025.105613.0625.160073.0263.2ˆ332z z z z y3、 4、 5、 6、 最优工艺条件 7、 最优凝固条件 即 8、.078.1=γ习题八习题九(1) E(5， , 0) (2)(i)扩大反射)1(>α；(ii)内收缩)0(<α；（iii ）反射收缩)10(<α<；(3)B(2,4,3)，A ＇(1.5,3,3.5),D ＇(2.5,2.5,2.5),C ＇(3,3.5,2)习题十1、 A 3B 3C 32、A 2B 3CD3、最优工艺条件x 1=-0.076,x 2=-0.118,即z 1=3. 848，z 2=0. 753，9.37ˆ=y4、 最优适宜条件 x 1=-0.0135, x 2=0.2557,x 3=-0.3364, 即z 1=6.4865, z 2=112.7865,z 3=0.3318.习题十一1、3.3962、3.54, 3.463、 5、6、 7、有系统误差2221212122212121z 9.21z 676.0z z 469.4z 465.50z 566.8572.2x504.3x 704.2xx 575.3x 1.1x 833.0838.37yˆ---++=-----=323121232221321x x 3.5x x 35.2x x 78.2x 38.3x 8.2x 1.3x 95.0x 388.0x 163.04.37y ˆ---------=.nσ.T2l g⎪⎭⎫⎝⎛σ+⎪⎭⎫⎝⎛σ≈σ.VMVV,VW W M σ+σ+σ≈σ-=.z 0019.0z 0148.0z 1388.0z 1269.06250.47yˆ4321--++=.z z 2.2z 15.058.125y ˆ321+++-=.z 0201.0z 00225.0z 00184.0z 000885.0114.0y ˆ4321-+--=,x 041.0x 023.0.x x 002.0x 052.0x 017.0351.0yˆ22212121--+++=.371.0yˆ,576.8z ,9.119z ,644.0x ,398.0x 2121=====即xx 02.0xx 025.0x025.0x475.0x 400.0218.89yˆ-+-++=,x 896.0x947.0x 399.0x x 375.023222132---+,0735.0x ,261.0x,483.0x 321===.38.89yˆ,02.6z ,13.4z ,42.17z 321====3108、无系统误差 9、是异常数据.习题十二1、543.02、(1)0.695 (2) (3)0.4253、(1)(2)2.98； (3) 0.898;4、(-1.28, -0.255, 0.675, 1.645)习题十四（1）一般； 2.5888（介于良与一般之间）；（2）68.2245分.习题十五1、{}{}6,5,4,3,2,12、{}{}6,5,4,3,2,1习题十六2、ρ︒复相关系数上的投影在是其中与;),,,(L ˆ,)ˆ(*p *2*1***o*x x x y y y y⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=16.0431.06.0165.0431.065.01R )10.1,10.1,27.0,55.0,37.1,55.0(x)28.1,91.0,18.0,18.0,91.0,28.1(x ---=---=参考文献[1] Andenson T W. An Introduction to Multivariate StatisticalAnalysis. znd ed . New york: Wiley, 1984[2] 费荣昌试验设计与数据处理，4(1997)[3] 方开泰实用多元统计分析，上海：华东师范大学出版社，1989[4] 盛骤等概率论与数理统计，北京：高等教育出版社，1989[5] 朱道元等多元统计分析与软件SAS，南京：东南大学出版社，1999[6] 彭昭英SAS系统应用开发指南，北京：北京希望电子出版社，2000[7] 邓勃分析测试数据的统计处理方法，北京：清华大学出版社，1995[8] 中国现场统计会三次设计组，正交法和三次设计，北京：科学出版社，1985[9] 张尧庭、方开泰多元统计分析引论，北京：科学出版社，1983[10] 上海师范大学数学系回归分析及其试验设计，上海：上海教育出版社，1978[11] 韦博成、鲁国斌统计诊断引论，南京：东南大学出版社，1991[12] 张明淳工程矩阵理论，南京：东南大学出版社，1995[13] 赵德齐模糊数学，北京：中央民族大学出版社，1995[14] 胡永宏、贺思辉综合评价方法，北京：科学出版社，2000[15] 张崇甫等统计分析方法及其应用，重庆：重庆大学出版社，1995[16] 蒋尔雄等线性代数，北京：人民教育出版社，1978[17]王松桂线性模型的理论及其应用，合肥：安徽教育出版社，1987。
数据分析与处理答案 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】一、 简答题（5×2分， 共10分）1、请解释质量控制图中三条主要控制线的意义：CL 、UCL 、LCL 未学，不考2、请解释正交设计表“L 934” 这个符号所指代的意义。
如果要做6因素4水平实验，应该选择以下哪一个正交表（不考虑交互作用）：L 1645，L 3249 L: 正交； 9：9行或9次实验； 3：3个水平 ； 4：4列或4个因素 选L 3249二、计算题（90分）1、某分析人员分别进行4次平行测定，得铅含量分别是、、、、，试分别用3s法、Dixon 法和Grubbs 检验法判断是否为离群值。
（，4=， ,5=）（12分）x =, s=,3s 法：∣ 应保留 Dixon ：70.6360.080.89671.8560.08Q -==-> ,5=, 应舍去Grubbs: G 计= 60.0868.455/5.61-=> ，4，应舍去···2、4次测定结果为：%、%、%、%，根据这些数据估计此样品中铬的含量范围（P=95%）？（8分）( 2.353%903,10.0=⇒=t P ， 3.182%9530.05=⇒=，t P ，5.841%9930.01=⇒=，t P )x =%, s=%3、用一种新方法测定标准试样中的氧化铁含量（%），得到以下8个数据：、、、、、、、。
标准偏差为%，标准值为%问这种新方法是否可靠（P=95%，，7=）（10分）x = 34.3034.331.770.048t -==< ，7，所以新方法可靠4、某小组做加标回收试验考查方法的准确性，测得加标前1000mL样品浓度为L，加入浓度为1000mg/L的标准样品后，测得样品总浓度为L，求回收率是多少。
（8分）没讲，不考5、两分析人员测定某试样中铁的含量，得到如下结果：已知A的标准偏差s1=，B的标准偏差s2=，请比较两个人测定结果的精密度和准确的有无显着性差异。
一、单选题（题数：50，共 50.0 分）1在正交实验设计中,定量因素各水平的间距是( )（1.0分）1.0分正确答案：C 我的答案：C答案解析：2*随机单位设计要求( )。
（1.0分）0.0分单位组内没有个体差异,单位组间差异大正确答案：A 我的答案：3当组数等于2时,对于同一资料,方差分析结果与t检验结果( ) 。
（1.0分）0.0分t检验结果更准确完全等价且正确答案：D 我的答案：B答案解析：方差分析与t检验的区别与联系。
对于同一资料,当处理组数为2时,t检验和方差分析的结果一致且,因此,正确答案为D。
4下列结论正确的是( )①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.（1.0分）0.0分正确答案：C 我的答案：5在对两个变量,进行线性回归分析时,有下列步骤:①对所求出的回归直线方程作出解释;②收集数据、),,…,;③求线性回归方程;④求未知参数; ⑤根据所搜集的数据绘制散点图。
如果根据可行性要求能够作出变量具有线性相关结论,则在下列操作中正确的是( ) （1.0分）0.0分正确答案：D 我的答案：6*方差分析中变量变换的目的是( )。
（1.0分）0.0分正确答案：D 我的答案：7两个变量与的回归模型中,通常用来刻画回归的效果,则正确的叙述是( ) （1.0分）0.0分越小,残差平方和越小越大,残差平方和越大与残差平方和无关越小,残差平方和越大正确答案：D 我的答案：答案解析：8在一个正交实验中,因素A和B的水平数都为3,那么A和B的交互作用的自由度为( )（1.0分）0.0分正确答案：C 我的答案：答案解析：9单因素方差分析中,当P<0.05时,可认为( )。
（1.0分）0.0分正确答案：B 我的答案：答案解析：方差分析的检验假设及统计推断。
方差分析用于多个样本均数的比较,它的备择假设(H1)是各总体均数不等或不全相等,当P<0.05时,接受h1,即认为总体均数不等或不全相等。
1.在^xcel中用AVERAGE函数计算平均值，用STEDV函数计算标准偏差，得到结果如表1所示。
表1该污水厂进、出水水质标准偏差及平均值COD SS 氨氮进水出水进水出水进水出水标准偏差102.70497 5.6417987 40.44311 2.2590321 7.7226061 1.1480863 平均值368.39 42.05 243.39 16.65 33.77 1.85图1该污水厂进、出水水质示意图2.在excel中作图如下:（1）加药量（mg/L）加药量（mg/L）图6加药量与浊度去除率、总磷去除率、总氮去除率、COD 去除率的关系图3. (1)图2总磷随加药质的变化关系图 图3余浊随加药质的变化关系图5075 100125150加药量(mg/L)5075100125150加药量(mg/L)图4总氮随加药■的变化关系图 图5 COD 随加药■的变化关系图(8)瓣泰2 0164 2108 6 4 (T/SUONH50 49 485756554 3 2 155 5 5 (q/SUIQooo o Oo o o o O图7进水量Q 与SVI 关系图10.015.020.025.030.035.0水温(笆)图8水温与SVI 关系图0.0010.00 20.00 30.00 40.00 50.00 60.00 70.00SV30 (%)图9 SV30与SVI 关系图0.00 20.0025.00 45.00 2(10(1HUM Hloo O oo O O.O.O. 8 6 430.0035.00 40.00 进水流量Q (万m3/d)50.00II)2((T /SUI0.002.004.006.00 8.0010.0012.00MLSS (g/L)图10 MLSS 与SVI 关系图(2) 用excel 中correl 函数求出相关系数r,再根据0V|rl<l,存在一定线性关系：①0 VlrlVO.3,微弱相关；②0.3VIHV0.5,低度相关;③0.5<lrl<0.8,显著相关；④0.8 <lrlVl,高度相关。
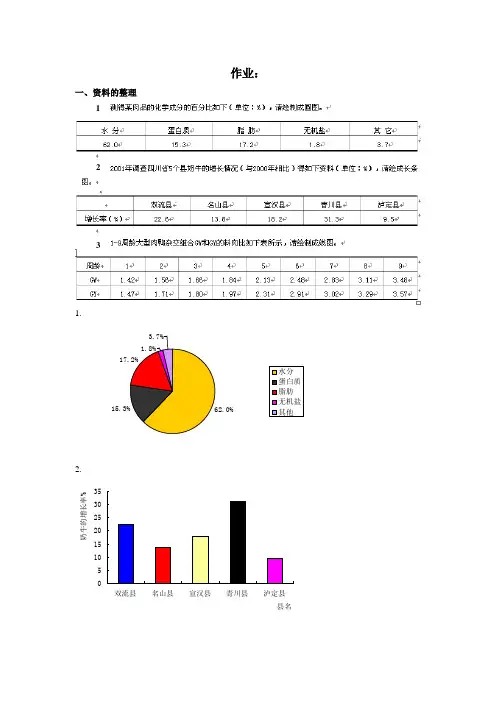
作业：一、资料的整理1.15.3%17.2%1.8%3.7%62.0%水分蛋白质脂肪无机盐其他2.5101520253035双流县名山县宣汉县青川县泸定县县名奶牛的增长率%1233.二、平均数、标准差1、10头母猪第一胎的产仔数分别为：9、8、7、10、12、10、11、14、8、9头。
试计算这10头母猪第一胎产仔数的平均数、标准差和变异系数。
（x =9.8头，S =2.098头，C ·V =21.40%）。
x =9.8头，S =2.098头，C ·V =21.40%2、调查甲、乙两地成年男性的体重（斤）如下表，试比较两地成年男性体重的变异程度。
甲地 137 133 130 128 127 119 136 132 乙地 128130129130131132129130（S 甲=5.75斤, C.V 甲=4.42%；S 乙=1.25斤，C.V 乙=0.96%）S=5.75斤，C.V=4.42%;S=1.25斤，CV=0.96%. 三、t 检验1、随机抽测了10只兔的直肠温度，其数据为：38.7、39.0、38.9、39.6、39.1、39.8、38.5、39.7、39.2、38.4（℃），已知该品种兔直肠温度的总体平均数0μ=39.5（℃），试检验该样本平均温度与0μ是否存在显著差异？（=t2.641 0.01<P <0.05）2、某猪场从10窝大白猪的仔猪中，每窝抽出性别相同、体重接近的仔猪2头，将每窝两头仔猪随机地分配到两个饲料组，进行饲料对比试验，试验时间30天，增重结果见下表。
试检验两种饲料喂饲的仔猪平均增重差异是否显著？（=t3.455 P <0.01）3、分别测定了10只大耳白家兔、11只青紫蓝家兔在停食18小时后正常血糖值如下，问该两个品种（=t12.455 P <0.01）四、方差分析第一题：单因素方差分析。
试检验这几种药物有没有差别。
16.为了比较4种饲料(A)和猪的3个品种(B)，从每个品种随机抽取4头猪(共12头)分别喂以4种不同饲料。
1、用Excel作出下表数据带数据点的折线散点图：（1）分别作出加药量和余浊、总氮T-N、总磷T-P、COD的变化关系图（共四张图，要求它们的格式大小一致，并以两张图并列的形式排版到Word中，注意调整图形的大小）；（2）在一张图中作出加药量和浊度去除率、总氮T-N去除率、总磷T-P去除率、COD 去除率的变化关系折线散点图。
【…2、对离心泵性能进行测试的实验中，得到流量Q v、压头H和效率η的数据如表所示，绘制离心泵特性曲线。
将扬程曲线和效率曲线均拟合成多项式。
（要求作双Y轴图）流量Qv、压头H和效率η的关系数据56序号123/4Q v(m3/h)H/m#η>9101112序号7)8Q v(m3/h)&H/mη:【3、用荧光法测定阿司匹林中的水杨酸（SA），测得的工作曲线和样品溶液的数据如下表:C(SA)/μ样品1样品2F(荧光强度)。
（1）列出一元线性回归方程，求出相关系数，并给出回归方程的精度；（2）求出未知液（样品）的水杨酸（SA）浓度。
(1)（C(SA)/μF(荧光强度){(2)4、对某矿中的13个相邻矿点的某种伴生金属含量进行测定，得到如下一组数据：矿样点距离x矿样点矿样点距离x|含量c128113914@23410！1545111657 (1218)68131910\7试找出某伴生金属c与含量距离x之间的关系(要求有分析过程、计算表格以及回归图形)。
提示：⑴作实验点的散点图，分析c~x之间可能的函数关系，如对数函数y=a+blgx、双曲函数(1/y)=a+(b/x)或幂函数y=dx b等；⑵对各函数关系分别建立数学模型逐步讨论，即分别将非线性关系转化成线性模型进行回归分析，分析相关系数：如果R≦，则建立的回归方程无意义，否则选取标准差SD最小（或R最大）的一种模型作为某伴生金属c与含量距离x之间经验公式。
上表为各种函数的对比由表可以看出多项式函数的R值最大，所以选择多项式函数。
5、在玻璃防雾剂的配方研究中，考察了三种主要成分用量对玻璃防雾性能的影响，三个因素的水平取值如下：因素 1 2 3[45 6 7PVA x 1/g（ZC x 2/g—LAS x 3/g试验结果y)已知试验指标y 与x 1 、x 2 、x 3间近似满足关系式：y ＝a+b 1x 1+b 3x 3+b 23 x 2x 3 。
试求待定系数，并给出方程精度。
项目 B 1 |B 3B 23 R 2 标准误差 a数值{6、 测定某铜合金中铜含量，五次平行测定的结果是：%、%、%、%、%，计算：（1）平均值；平均偏差；相对平均偏差；标准偏差；相对标准偏差；（2）若已知铜的标准含量为%，计算以上结果的绝对误差和相对误差。
解：(1) 平均值：x =nx i∑=%平均偏差：d =()nx x i∑- =%相对平均d /x =%/%)*100%=%标准偏差：S=()12-∑-n i xx =%~相对标准偏差:S r =S/x=%（2）绝对误差= x–μ=%%=%相对误差=（x–μ）/μ=%7、已知某合成试验的反应温度范围为340～420℃，通过单因素优选法得到：温度为400℃时，产品的合成率最高，如果使用的是法，问优选过程是如何进行的，共需作多少次实验。
假设在实验范围内合成率是温度的上单峰函数。
(要求详细列出计算过程)解：由题知，所给范围合成率是温度的上单单峰函数由法在区间(340,420)进行优选。
X1=340+(420-340)=X2=340+(420-340)=比较389℃和371℃下的实验数据，得389℃的数据较好,所以去掉340～370℃。
再次优选X3=370+(420-370)=401）X4=370+(420-370)=389由于389℃已在试验点，所以只需做三次不同温度的实验。
实验范围内合成率是温度的上单峰函数所以选择在401℃数据较好。
8、某农科站进行品种试验，共有4个因素：A（品种）、B（氮肥量/kg）、C（氮、磷、钾肥比例）、D（规格）。
因素A有四个水平，另外三个因素都有两个水平，具体数值如下表所示。
试验指标是产量，数值越大越好。
试验结果（产量/kg）依次为：195、205、220、225、210、215、185、190。
试找出最好的实验方案。
i=1234序号因素A B C、产量/kgD111111952220521、2321122202221225|453122101632122152218574】184211190400810820820{K1iK2i445835825>825K3i425K4i375（ki2444200205205:K1i/kiK2i/ki【K3i/kiK4i/ki.极差35$从上表可以看出，因素A的极差最大，因此A对实验的影响最大，因素B的极差仅次于A，对实验影响也仅次于A，因素C、D对实验影响较小，都以2水平较好。
因此最优实验方案为A2B2C2D2。
9、阅读下列材料：在高层建筑基础(如钻孔灌注桩和地下连续墙) 的施工过程中通常采用泥浆护壁技术,因此而产生大量的废弃泥浆,泥浆中含有大量的蒙脱石等粘土矿物和岩屑,稠度大,既不能直接排放,又难于自然沉降。
若不及时处理,不但影响施工,而且会造成环境污染或水质污染等二次公害。
废泥浆处理已成为施工单位和环卫部门十分关注的问题。
我们采用正交法安排试验,正交试验法是一种科学安排与分析多因素试验的方法。
通过正交试验法所特有的科学分析方法,用少数试验所获得试验数据,可推导出具有说服力的正确结论。
如:因素的主次关系、最优参数组合、指标与因素的关系等。
首先让泥浆固液分离,然后对固相进行强制脱水或化学固化。
本文着重讨论废泥浆固液分离的正交试验。
⑴固液分离中固相凝聚与絮凝的机理由于泥浆中的固相膨润土的吸水率强,颗粒表面积大,吸附阴离子而形成负溶胶。
向泥浆中投放混凝剂,通过物理的或化学的反应,使泥浆胶体脱稳而凝聚,从而达到泥水分离的目的。
混凝剂主要包括凝聚剂和絮凝剂。
所谓凝聚剂就是在分散体系中加入无机电解质,通过电性中和、压缩双电层、降低Zeta 电位,减少微粒间的排斥能,从而达到聚凝的目的。
常用的无机凝聚剂有FeCl3·Al2(SO4)3、Ca(OH)2等。
所谓絮凝剂就是带有许多活性官能团的高分子线状化合物;通过架桥作用,高分子絮凝剂能将许多微粒聚集在一起,形成一些较大体积的松散絮团,从而达到絮凝的目的。
常见的高分子絮凝剂有聚丙烯酰胺、聚乙烯胺等。
凝聚剂与絮凝剂两者可分别单独使用,也可根据各自性质组合使用。
⑵泥浆配制用膨润土制备不同浓度的泥浆,并加入增粘剂(为水重的0。
05%) 、分散剂(为水重的0。
2%) ,配成性能稳定的泥浆(接近工程用浆) 。
本次试验配备了3 个浓度泥浆(膨润土的含量为5%、8%、10%) 。
混凝试验在玻璃量筒中进行。
⑶正交试验方案设计正交试验设计就是利用一种规格化的表格——正交表来合理安排试验,其特点: ①每个不同水平在试验中出现相同次数; ②任何两个因素的任一水平搭配都出现一次,它具有因素搭配均衡的特点。
因此,正交试验法安排的试验是具有代表性的,能够较全面地反映各水平对指标影响。
本次试验选用正交表L27（313）安排试验,如表2 ,通过27次试验可代表81种情况。
正交试验方案设计包括: ①确定试验指标、因素和水平; ②选定正交表; ③设计表头;④列出试验方案。
指标:表征试验研究对象的指标。
本试验选用固相沉降率(上层清液体积与原浆体积之比) 和固相沉降速度为指标,来评定混凝效果。
因素:对试验指标可能会产生影响的要素,本试验中选用泥浆浓度、混凝剂种类、混凝剂的加量和搅拌时间为试验的“因素”。
水平:因素在试验中所选取的具体状态称为“水平”,本试验中均取3 个水平见表1。
￥试根据所给材料，对表2的试验结果进行分析：⑴对表2的试验结果进行数据处理，单独列出固相沉降率的试验分析表；⑵根据试验分析表的数据，讨论各因素对混凝效果（即试验指标）影响的主次顺序以及最佳处理组合；⑶绘制水平影响趋势图，并进行简要分析。
解：（1）t= 1min的分析表1如下序号i=1234.因素泥浆浓度A混凝剂种类B加量C时间DK1i25539180210|K2i187******** K3i175535225189、ki9999 K1i/ki2842023~K2i/ki2152424 K3i/ki19592521~极差95553由表1可以看出在t=1min时最佳方案是A1B3C3D2 t= 1h的分析表2如下序号i=12*34因素泥浆浓度A 混凝剂种类B加量C时间DK1i586428;476515K2i509463536501K3i467671】550546ki9999K1i/ki65485357K2i/ki57516056K3i/ki52756161极差132785由表2可以看出在t=1min时最佳方案是A1B3C3D2(2) 由（1）中表1和表2可以看出对于沉降率的影响由大到小依次是混凝剂种类、搅拌时间、加量、泥浆浓度，与沉降时间影响最小。
由于考虑经济效益，优先考虑搅拌时间，最佳选择A1B3C3D2即为最佳查理组合为泥浆浓度为5%，混凝剂种类(CO2CHCONH2)n，加量为20mL，搅拌时间为5分钟（3）图1、2、3、4为t=1min的坐标图。
图5、6、7、8为t=1h的坐标图。
10、结合自己的专业谈一谈学习本门课程的感受（收获与建议，不少于100字）。
通过为期将近2个月的学习，真的是收获了很多，才发现以前所掌握的一些excel用法是那么的浅显而不足。
不长的时间里，我学会了一些origin 和excel 的一些基本用法以及一些今后都会用到的实用技巧，虽说刚开始较晦涩难懂，但通过不断地练习与作业，总算能够独立的处理一些问题，为简便算法和步骤节约了时间。
能学会很好的处理数据和作图是这学期学习的基本要求，学会如何理解和列出多因素正交实验设计图及其设计方法，如法，对分法，均分法等，也学会如何对一系列的点做各种函数拟合来得到较优的拟合结果，以及单变量求解和各种函数计算，如加和，求均值，求标准偏差等，。
学习也不是一蹴而就，刚开始的时候可以说什么都不懂，通过同学间的相互帮助，耐心讲解，才逐渐学会怎样更好更快捷的使用那些技能。
所以说，学习也不是一个人的事，而是大家一起帮助一起成长的事。
总而言之，这门课程不仅让我学会了新的软件用法，拓宽了知识面，也明白了自己的不足，而且还提高了学习效率，是一门很实用很有效率的课程。
