当前位置：文档之家 › 第三节 三重积分的概念及性质

第三节 三重积分的概念及性质

  • 格式：pdf
  • 大小：121.10 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

三重积分

三重积分

∫∫∫ ( x2 + 5xy2 sin x2 + y2 )d x d y d z, 其中 Ω
Ω 由 z = 1 (x2 + y2 ), z = 1, z = 4围成. 2
解: I = ∫∫∫Ω x2 d x d y d z+ 5 ∫∫∫Ω xy2 sin x2 + y2 d x d y d z
利用对称性
∫∫ ∫ 记作 dxdy z2 (x, y) f (x, y, z)dz
D
z1( x, y)
z = z1(x, y)
y xD
dxd y 微元线密度≈ f (x, y, z) dxd y
1
例 1 化三重积分 I = ∫∫∫ f ( x, y, z)dxdydz为三
Ω
次积分，其中积分区域Ω为由曲面 z = x2 + 2 y2
Ω
D
z1( x, y)
方法2. “先二后一”
∫∫∫Ω
f
(
x,
y,
z
)
d
v
=
∫b a
d
z
∫∫DZ
f (x, y, z)dxdy
方法3. “三次积分”
∫∫∫ ∫ ∫ ∫ f (x, y, z)d v = Ω
b
dx
y2 (x) d y
a
y1( x)
z2 (x, y) f (x, y, z)d z
z1( x, y)
z
1
o
1
x
y
1
例 3 化三重积分∫∫∫ y 1 − x2dxdydz为三次积分，其中 Ω
Ω 由曲面 y = − 1 − x2 − z2 ， x2 + z2 = 1， y = 1所围成.

第三节三重积分的概念与计算

第三节三重积分的概念与计算
过 z轴且平行 xoy平面的平面去截 ，得截面
Dz ，则三重积分的计算可化为先对
z
x，y 求二重积分，再对 z 求定积分， b
即
Dz
f(x, y,z)dxdydz
b
a
dz f(x,y,z)dxdy
第八章 重积分 第三节 三重积分的概念与计算
一、三重积分的概念
问题的提出： 设空间立体 V 的密度函数为 f ( x, y, z )，求立体 V 的质量 M
为了求 V 的质量，仍采用：分割、近似代替、
求和、取极限四个步骤.
首先把 V 分成 n 个小块 V1 , V2 , . . . , Vn , Vi 的体积 记为 V i
x
zz2(x,y)
z2 S2
z1 S1
zz1(x,y)
D
(x, y) yy1(x)
y
yy2(x)
先x将 ,y看作定 f(x,值 y,z)只 ， 看 z的 将 作 函数，则
F (x,y)z2(x,y)f(x,y,z)dz z1(x,y)
再计F算 (x,y)在闭区 Dx间 y上的二重积分
f(x ,y ,z )d vF (x ,y )d[z 2 (x ,y )f(x ,y ,z )d ] d z.
VVdxdydz
例 3 求由曲面 z x2 2 y2及z 2 x2所围成 的闭区域 的体积.
解 由zzx222x2y2,
得 交 线 投 影 区 域 x2y21,
故 {x (,y,z)|x22y2z2x2,(x,y) D x}y 其D x 中 y {x (,y)|x2y21 }
的体积 1dxdydz
Dxy
Dxy
1
1x
xdx2 (1x2y)dy

三重积分的定义和性质

三重积分的定义和性质

三重积分的定义和性质三重积分是微积分中一种用于计算三维空间中曲面下体积、质量等物理量的方法。

在学习三重积分之前，我们需要了解它的定义和性质，以便能够正确地应用于问题的求解。

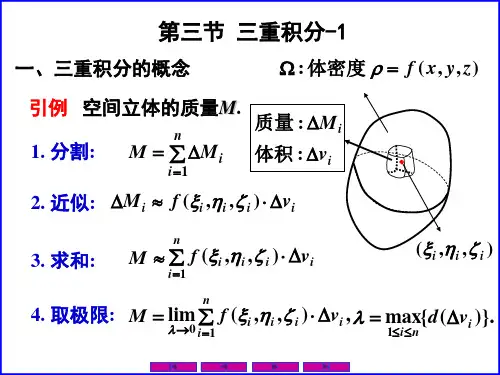
一、三重积分的定义三重积分的定义可以通过对立体进行切割、求和的方法来理解。

我们将三维空间切割成许多小的体积元，每个小体积元的体积近似于一个长方体。

假设我们要计算的函数为f(x,y,z)，则三重积分的定义可以表示为：∭f(x,y,z)dV = lim Σ f(x_i,y_i,z_i)ΔV其中，Σ表示对所有小体积元的求和，每个小体积元的体积为ΔV，该体积元的中心坐标为(x_i,y_i,z_i)。

当每个小体积元的体积趋近于零时，求和变成了对整个区域进行积分。

二、三重积分的性质1. 可加性三重积分具有可加性，即对于两个子区域A和B，有以下关系成立：∭(A∪B)f(x,y,z)dV = ∭Af(x,y,z)dV + ∭Bf(x,y,z)dV这意味着我们可以将一个复杂的区域划分成多个简单的子区域进行计算，再将结果进行相加，从而简化计算过程。

2. 反序性三重积分的计算顺序可以灵活选择，即可以按照x、y、z的任意次序进行求解。

这种性质的使用可以根据问题的要求来确定最佳求解顺序，从而简化计算过程。

3. 坐标变换在实际问题中，我们经常遇到需要进行坐标变换的情况。

通过适当的坐标变换，可以将原来的坐标系转化为更便于计算的形式。

常见的坐标变换包括柱坐标和球坐标等。

三、应用举例三重积分的应用非常广泛，下面举几个例子来说明其在实际问题中的应用。

例一：计算立体的体积假设我们需要计算一个球体的体积，其半径为R。

我们可以将球体切割成许多小的体积元，然后对所有体积元进行求和，即可得到球体的体积。

例二：计算立体的质量假设我们有一个密度分布函数为ρ(x,y,z)的立体，我们想要计算该立体的质量。

可以将立体切割成小的体积元，然后对每个体积元的质量进行求和，即可得到整个立体的质量。

三重积分的定义及性质

三重积分的定义及性质


0
f x, y, z f x, y, z


Байду номын сангаас
2
1
f
x,
y, z dv
f x, y, z f x, y, z
1 为 的对称部分中的一部分.
4、设积分区域 关于原点对称，则
f x, y, z dv

0



1、设积分区域 关于 xoy 坐标面对称，则
f x, y, z dv


0



2
1
f
x,
y, z dv
f x, y,z f x, y, z f x, y,z f x, y, z
1 为 的对称部分中的一部分.
2、设积分区域 关于 yoz 坐标面对称，则
n
并作和： f i ,i , i vi , i 1
设 是各小区域的直径中的最大值. 如果极限：
n
lim f
0 i1
i ,i , i
vi 存在,
则称此极限为函数 f x, y, z 在区域 上的三重积分.
记作： f x, y, z dv
i ,i , i
vi
定义 设 f x, y, z 是有界闭区域 上的有界函数.将
闭区域 任意分成 n 个小闭区域： v1 , v2 , …, vn ，其中 vi 也代表第 i 个小块的体积.
在每个 vi 上任取一点 i ,i , i ,作乘积：
f i ,i , i vi ( i 1, 2, , n ),


例 计算

0903三重积分-1

0903三重积分-1
过点 ( x , y ) ∈ D 作直线 , 穿出． 从 z1 穿入 , 从 z2 穿出．
x
o
z1
z2 S 2
Ω
S1
z = z1 ( x , y )
D
( x, y)
y
Ω = {( x , y , z ) | z1 ( x , y ) ≤ z ≤ z2 ( x , y ), ( x , y ) ∈ D }.
Ω
1
1− x
1− x − y
0
z dz
z
1 1 1− x 2 = ∫0 dx ∫0 (1 − x − y ) dy 2
1
1 1 1 3 = ∫0 (1 − x ) dx = . 6 24
o
y
1
x
1
读题 计算三重积分∫∫∫ z2dxdydz,其中Ω是由椭球面
x2 a2
+
y2 b2
+
z2 c2
Ω
= 1(a, b, c > 0)所围成的空间有界闭区 . 域
Ω
Ω1
Ω2
性质4 性质4 三重积分的几何意义 : ◆计算 ∫∫∫ 1 ⋅ dv = ∫∫∫ dv = ? 的体积 . Ω
Ω Ω
性质5 比较性质: 性质5 比较性质: 若在Ω上, 有 f ( x , y , z ) ≤ g ( x , y , z ),
则有
∫∫∫ f ( x , y, z )dv ≤ ∫∫∫ g( x , y, z )dv .
1.先将 x , y 看作定值 , 将 f ( x , y , z )只看作 z 的函数 , 则 :
∫
z2 ( x , y ) f ( x , y , z )dz = F ( x , y ) → 面密度函数; z1 ( x , y )

10-5 三重积分的概念与性质 (1)

10-5 三重积分的概念与性质 (1)

x
y
Dxy : x 2 y2 4.
zdv

2
2 1 2 64 4 d (16 )d . 0 2 0 3
0
d d 2 zdz
0
2
4

12
(2)当 f ( x , y, z ) 在闭区域上连续时， 定义中和 式的极限必存在，即三重积分必存在.
(3)三重积分与二重积分有类似的性质。 (4)三重积分的物理意义：如果被积函数表示空 间物体的体密度，则三重积分表示物体的质量。
4
三重积分的直角坐标形式
z
已知三重积分存在的前提下 在直角坐标系下用平行于三 个坐标面的三组平面来划分区域 Ω，则典型小区域是长方体，
第十章 重积分
第三节 三重积分的概念
1
一、三重积分的概念
定义 设 f ( x , y, z ) 是空间有界闭区域 上的有界 ， 函数，将 任意分成 n 个小闭区域 v1 ， v2 , 上任取一点 (i ,i , i ) ， 作乘积 f (i ,i , i ) v i ， 并作和
在每个 vi vn ， v i 也表示第 i 个小闭区域的体积，
( i 1,2,, n) ，
f ( , , )v ，
i 1 i i i i
2
n
如果当各小闭区域的直径中的最大值 趋近于零 时，这和式的极限存在，则称此极限为函数 f ( x, y, z ) 在闭区域 上的三重积分， 记为
o
x
v
x
z
y
y
则体积元素为 dv xyz dxdydz
故三重积分可写为
f ( x, y, z )dv f ( x, y, z )dxdydz.

10.3三重积分

10.3三重积分

M =lim∑µ(ξi ,ηi ,ζi )∆vi
λ→0 i=1 =
n
∆vi
o x
(ξi ,ηi ,ζ i ) y
定义 设 f ( x, y, z)(( x, y, z)∈Ω) 若对 Ω 作任意分割: 任意分割: 任意取点 积和式” 极限 积和式”
lim∑ f (ξi ,ηi ,ζ i )∆vi
λ→0
n
i
)∆v i .
∫∫∫ f ( x, y, z )dv = lim ∑ f (ξ ,η , ζ λ
Ω →0 i =1 i i
n
i
)∆v i .
说明 (1) 在直角坐标系下常写作 dv = dxdydz. (2) 三重积分的性质与二重积分相似. 三重积分的性质与二重积分相似. 例如 线性性质、对积分区域的可加性、比较性质、 线性性质、对积分区域的可加性、比较性质、 估值性质、中值定理，还有 估值性质、中值定理，
1
D xy o
y
= ∫ dx ∫
−1
1− x
2 2
− 1− x
dy ∫
2− x − y
2
2
x
x +y
2
2
f ( x , y , z )dz
方法2 方法2 截面法 (“先二后一”) (“先二后一 先二后一”
(1) 将Ω向 z 轴投影，得投影区间[c1 , c2 ].
z
(2) 任取z ∈ [c1 , c2 ]，过 z作平行于xoy坐标 z 面的平面去截Ω，得截面Dz c1 ( x , y ) ∈ Dz o 则 Ω c1 ≤ z ≤ c2 x
例2 化 ∫∫∫ f ( x , y , z )dxdydz为三次积分，其中Ω为由

第三节 三重积分

第三节 三重积分
z
规定： 0 r ,
0 2,
z .
2020/3/11
第十章 第三节
• M(x, y,z)
o

x
r
y
•
P(r, )
24
如图，三坐标面分别为
r 为常数
为常数
z 为常数
圆柱面； 半平面； 平 面．
z
• M (x, y, z)
z
or
• P(r, )
f (i ,i , i )vi .
其中dxdydz 叫做直角坐标系中的体积元素.
2020/3/11
第十章 第三节
4
当函数f(x,y,z)在Ω上连续时,(1)式右端的和式极限
必定存在,也就是函数f(x,y,z)在区域Ω上的三重积分必
定存在,以后我们总假设函数f(x,y,z)在Ω上是连续的,
关于二重积分的一些概念都可相应地用于三重积分.
(1 x4)dydz
D
2
y2 z2x2

4 (1 x4 )x2dx [ x3
2
3

x7 7
]42
( 43 23 47 27 ) 2340 20
3
7
21
2020/3/11
第十章 第三节
19
例题: 求曲面z 4a2 x2 y2与 z x2 y2 所围立体体积。
d
x
f (r cos ,r sin , z)rdrddz.
2020/3/11
第十章 第三节
26
一般适用情形
1 积分域表面用柱面坐标表示时方程简单,当积分 区域为柱体，椎体，或由柱面，锥面，旋转抛物 面与其他曲面所围形体；

8-3(1)三重积分

8-3(1)三重积分
1 ∫∫ dxdy = 2(1 − z )(1 − z ) D 1 1 1 2 . 原式= ∫ z ⋅ (1 − z ) dz = 0 2 24
z
Dz
o
1
y
x
1
Dz的面积
22
解法2 解法2：
z
∫∫∫ zdxdydz = ∫0 zdz ∫0 dy ∫0
Ω
1
1− z
1− y − z
1
dx
o
y
= ∫0 zdz ∫0 (1 − y − z )dy
∑ µ(ξk ,ηk ,ζ k )∆vk
k=1
n
∆vk
(ξk ,ηk ,ζ k )
2
2、三重积分的定义
上的有界函数， 设 f ( x , y , z ) 是空间有界闭区域 Ω 上的有界函数， 将闭区域 Ω 任意分成 n个小闭区域 ∆v1， ∆v2 ,⋯, ∆v n ， 个小闭区域，也表示它的体积, 其中 ∆v i 表示第 i 个小闭区域，也表示它的体积, 在每 个 ∆vi 上任取一点 (ξ i ,η i , ζ i ) 作乘积 f (ξ i ,η i , ζ i ) ⋅ ∆vi ， ( i = 1,2,⋯, n) ，并作和, 如果当各小闭区域的直径中 并作和, 趋近于零时，这和式的极限存在， 的最大值 λ 趋近于零时，这和式的极限存在，则称此 极限为函数 f ( x , y , z ) 在闭区域 Ω 上的三重积分， 上的三重积分， 三重积分 记为 ∫∫∫ f ( x , y , z )dv ,
(3)计算二重积分 ∫∫ f ( x , y , z )dxdy 计算二重积分
Dz
z
其结果为 z 的函数 F (z ) ； (4)最后计算单积分 ∫ F ( z )dz 即得三重积分值 最后计算单积分 即得三重积分值.

(完整版)10.3三重积分(新)

(完整版)10.3三重积分(新)
0
8
dz
2
2
d
0
4 r 2 rdr
2
8
r2 dz
2
336
另 解2
8
I dz
( x2 y2 )dxdy
2
Dz
8
2
dz d
2z r 3dr
2
0
0
336 24
4、利用球面坐标计算三重积分
设 M (x, y, z) 为空间内一点，则点M 可用三个有次序的数
r，， 来确定，其中r 为原点O 与点 M 间的距离， 为有向 线段 OM与 z 轴正向所夹的角， 为从正 z 轴来看自x 轴按逆时
d
y
f (r sin cos ,r sin sin ,r cos )r2 sindrdd .
27
例1. 计算三重积分 (x2 y2 z2) d xd yd z ,其中为
锥面 z x 2 y 2 与球面 x2 y 2 z 2 R2 所围立体.
0rR
解:
在球面坐标下
:
0
0
4
b
(
( y2 ( x)
z2( x, y) f ( x, y, z)dz)dy)dx
a y1( x) z1( x, y)
b
dx
y2 ( x) dy z2 ( x, y) f ( x, y, z)dz.
a
y1( x)
z1( x, y)
6
例1. 计算三重积分 xd xd yd z 其中为 z
针方向转到有向线段OP 的角，这里 P 为点 M 在 xoy 面上的投
影，这样的三个数r，， 就叫做点 M 的球面坐标．
规定：
0 r , 0 , 0 2.

三重积分精讲

三重积分精讲

AB = r sin ϕ dθ .
o
B1
y
x
2
A1
AD AC AB = r sin ϕ drd ϕ d θ .
求半径为a的球面与半顶角为 例4 求半径为 的球面与半顶角为α的内接锥面所围成的 含有球心的立体的体积. 含有球心的立体的体积. 该立体所占区域Ω可表示为: 解 该立体所占区域Ω可表示为: 0≤r≤2acosϕ, 0≤ϕ≤α, 0≤θ≤2π. ≤≤ ≤ ≤ 于是所求立体的体积为
0
r θ
ϕ
M ( r , ϕ ,θ )
y
P
x
几何图形的表示
r=a θ =α
半径为a的球面 半径为 的球面 圆锥面 平面
ϕ=β
变量的变化范围
0 ≤ r < +∞ , 0 ≤ θ ≤ π , 0 ≤ ϕ ≤ 2π
直角坐标与球面坐标的关系 x=rsinϕcosθ, y=rsinϕsinθ, z=rcosϕ. = = = 球面坐标系中的体积元素 dv=r2sinϕdrdϕdθ. = 球面坐标系中的三重积分
下页
求半径为a的球面与半顶角为 例4 求半径为 的球面与半顶角为α的内接锥面所围成的 立体的体积. 立体的体积. 该立体所占区域Ω可表示为: 解 该立体所占区域Ω可表示为: 0≤r≤2acosϕ, 0≤ϕ≤α, 0≤θ≤2π. ≤≤ ≤ ≤ 于是所求立体的体积为
V = ∫∫∫dxdydz = ∫∫∫r2 sin ϕdrdϕdθ
D
D
= ∫∫ ρ 2 sin 2 θ (4 − ρ 2 ) ρ d ρ dθ
D
=∫
2π
0
sin θ dθ ∫ ρ 2 (4 − ρ 2 ) ρ d ρ
2 0

第三节 三重积分

第三节 三重积分
第三节 三重积分
一、三重积分的概念 三重积分的概念 二、三重积分的计算 1.直角直角坐标系下 直角直角坐标系下 直角 2.柱坐标下计算三重积分 柱坐标下计算三重积分 3.球坐标下计算三重积分 球坐标下计算三重积分
第十章
1
一、三重积分的概念
引例: 引例 设在空间有限闭区域 Ω 内分布着某种不均匀的 物质, 物质 密度函数为 µ( x, y, z) ∈C,求分布在 Ω 内的物质的 质量 M . 解决方法: 类似二重积分解决问题的思想, 解决方法 类似二重积分解决问题的思想 采用 “大化小 常代变 近似和 求极限” 大化小, 常代变, 近似和, 求极限” 大化小 可得 Ω
a
b
DZ
f ( x, y, z)dxdy
z2 ( x, y)
方法3. 三次积分 三次积分” 方法 “三次积分”
= ∫ d x∫
a
b
y2 ( x)
y1 ( x)
d y∫
z1 ( x, y)
f ( x, y, z)d z
三种方法(包含 种形式 各有特点, 三种方法 包含12种形式 各有特点 具体计算时应根据 包含 种形式)各有特点 被积函数及积分域的特点灵活选择. 被积函数及积分域的特点灵活选择
D
1
z2 ( x , y )
Ω
z1(x,y)
M
0
. .
y
D
x
P
10
2.计算三重积分 2.计算三重积分
I = ∫∫∫ f ( x, y, z )dxdydz
Ω
积分区域是曲顶柱体
z
z2(x,y)
Ω为图示曲顶柱体
I =∫∫ dxdy∫z ( x , y ) f ( x , y , z )dz

第三章 重积分及其应用 第三节 三重积分

第三章 重积分及其应用 第三节 三重积分

z
z
z 1
x y
2
2
1
2
z dz
4
31 5
o
y

- 13 -
x
第三节
三重积分
三
重积分在柱坐标系下计算
3
设 M ( x , y , z ) R , 将 x , y用极坐标 , 代替, 则 , , z ) （
第 就称为点M 的柱坐标. 直角坐标与柱面坐标的关系: 九 章 0 x cos z 0 2 重 y sin 积 ( ) z zz 分 M ( x, y, z ) z 及 其 坐标面分别为 应 用 圆柱面 常数 o y 常数 半平面 ( x , y ,0) x 平面 z 常数
解: 在柱面坐标系下 : 0 2 cos
2 cos
原式

z

2
d d d z
o
y
0

2
d

2
0
2 cos
d
2
0 zdz
8 9 a
3
a
x
y
z0

4a 3
2
2 cos
x
0
cos d
3
o
- 17 -
第三节
三重积分

y
y z 1
z
1
0 dz 1 1 z dy 0 2 2
f ( x , y , z ) dx
y
1 2

1 2
z
y 1 z
o
- 10 -

三重积分的积分性质和计算规则

三重积分的积分性质和计算规则

三重积分的积分性质和计算规则三重积分是数学中的一个重要概念，它在物理、工程、计算机科学等领域被广泛应用。

三重积分的计算需要掌握一些性质和规则，本文将详细介绍三重积分的积分性质和计算规则，以帮助读者更好地掌握这一知识点。

一、三重积分的定义三重积分是指对三维空间内的一个体积区域进行积分运算，其数学表达式为：$$\iiint\limits_{V}f(x,y,z)\mathrm{d}V$$其中，$V$ 表示积分区域，$f(x,y,z)$ 表示被积函数，$\mathrm{d}V$ 表示体积元素。

二、三重积分的积分性质1. 可积性若$f(x,y,z)$在闭合的积分区域 $V$ 上连续，则其在 $V$ 上可积。

2. 线性性设$f(x,y,z)$和$g(x,y,z)$在闭合的积分区域 $V$ 上可积，$k$为常数，则有：$$\iiint\limits_{V}(kf(x,y,z)+g(x,y,z))\mathrm{d}V=k\iiint\limits_ {V}f(x,y,z)\mathrm{d}V+\iiint\limits_{V}g(x,y,z)\mathrm{d}V$$3. 保号性设$f(x,y,z)$在闭合的积分区域 $V$ 上可积，则有：$$\iiint\limits_{V}f(x,y,z)\mathrm{d}V\geq0$$当且仅当 $f(x,y,z)$在 $V$ 上恒为 $0$ 时，等号成立。

4. 区域可加性设积分区域 $V$ 可以分成若干个不相交的子区域$V_1,V_2,\cdots,V_n$，则有：$$\iiint\limits_{V}f(x,y,z)\mathrm{d}V=\sum_{i=1}^{n}\iiint\limi ts_{V_i}f(x,y,z)\mathrm{d}V$$三、三重积分的计算规则1. 直角坐标系下的计算在直角坐标系下，我们可以将积分区域先按照 $x,y,z$ 的顺序分解，将三重积分化为三重定积分，然后按照积分顺序先计算$z$ 再计算 $y$ 最后计算 $x$。

21.5三重积分

21.5三重积分
V
例5 计算由平面 3 x y z 1, x 3 y z 1 以及 x y 3 z 1 所围成的平行六面体的体积. ( 1 / 2 )
(1) 柱面坐标变换
命题 2 设 f ( x , y, z ) 在有界闭区域 V 上可积, V 在变换
x r cos , 0 r , T : y r sin , 0 2 , z z, z 之下的原象为V , 则
V { ( x , y, z ) ( x , y ) Dxy , z1 ( x , y ) z z2 ( x , y )}.
此时,
f ( x, y, z )dxdydz dxdy
V D xy
z2 ( x , y )
z1 ( x , y )
f ( x, y, z )dz.
f ( x, y, z )dxdydz f (r cos , r sin , z )rdrddz.
V V
例6 设 V 是由曲面 z 2( x 2 y 2 ) 与 z 4 所围成的区域, 求 ( x 2 y 2 )d xdydz. ( 8 / 3 )
V
例7 求由曲面 z x 2 y 2 , z 2( x 2 y 2 ), y x 与 y x 2 所围成的立体体积 ( 3 / 35 ) .
(2) 球坐标变换
命题 3 设 f ( x , y, z ) 在有界闭区域 V 上可积, V 在变换
x r sin cos , 0 r , T : y r sin sin , 0 , z r cos , 0 2 之下的原象为V , 则
(2“平面夹” 型区域及“3 1 2” )
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 2
性质 4
d v V

（Ｖ为区域 的体积）．
性质 5
如果在 上，f ( x, y, z) g ( x, y, z) ，则有不等式
f ( x, y, z) d v g ( x, y, z) d v

特殊地有
f ( x, y, z) d v
质量可表示为
( x, y, z) d v．

三重积分的存在性： 当函数 f (x，y，z) 在闭区域 上连续时，函数 f(x，y，z) 在
上的三重积分是存在的，以后也总假定 f(x，y，z) 在闭区域 上是连续的．
二、三重积分的性质
性质 1
kf ( x, y, z) d v k f ( x, y, z) d v
f ( x, y, z) d v f ( y, x, z) d v

例1 设 : x 2 y 2 z 2 R 2 , z 0, 1 为 位于第一卦象内部分，
I1 ( xy 2 z )dv, I 2 xdv, 则（ ）．

(k 为常数)．
性质 2
[ f ( x, y, z) g ( x, y, z)]d v f ( x, y, z) d v g ( x, y, z) d v.

性质 3 如果闭区域 划分为两个闭区域1与 2 ，则
f ( x, y, z) d v f ( x, y, z) d v f ( x, y, z) d v
1
(A) I1 0
(C) I1 2 I 2
(B) I 2 0
(D) I1 4 I 2
解
I1 xy 2 dv zdv,

0 4 zdv 4 xdv
1
1
答案为Ｃ．
例２ 设 t : x y z t (t 0) 函数f ( x, y, z )在
f(x ，h ，z ) v f(x，y，z)dv lim l

0
i i i
i 1
n
i
．


积分号，
被积函数， 被积表达式，
f(x，y，z) f(x，y，z)dv
dv
x，y，z
体积元素，
积分变量， 积分区域，

f(x ，h ，z ) v
i i i
i 1
n
i
积分和．
三重积分的物理意义 若物体占有空间区域 ，且体密度函数为 ( x, y, z ), 则该物体的
i 1
如果当各小闭区域的直径中的最大值l趋于零时， 这和的极限总 存在， 则称此极限为函数f (x，y，z)在闭区域 上的三重积分，
记作 f(x，y，z)dv ， 即

f(x ，h ，z ) v f(x，y，z)dv lim l

0
i i i
i 1
n
i
．
三重积分中的有关术语：
第三节 三重积分的概念与性质
一、三重积分的定义
二、三重(x，y，z)是空间有界闭区域 上的有界函数．将 任意 分成 n 个小闭区域 v1，v2，· · · ，vn 其中vi表示第 i 个小闭区域，也表示它的体积．在每个vi上任 取一点(xi，hi，zi)，作乘积f(x i，h i，z i) vi（i1，2，· · · ，n)并 作和 n f(xi，hi，zi) vi．
2 2 2 2
f ( x, y, z)dv
点( 0, 0, 0 )的某个邻域内连续，求 lim
t 0 t
t
3
.
解 由积分中值定理可知 (xt ,ht , z t ) t 使得

t 0
lim
t
3 4 t f ( x, y, z )dv f (xt ,ht , z t ) 4 3 f (0, 0, 0) lim 3 3 t 0 3 t t
f ( x, y, z) d v 0.

(2) 如果
某一侧部分，且f (x, y, z)关于z(或y或x)为偶函数，则
关于xOy(或xOz或yOz) 对称，1 为 在相应的坐标面
f ( x, y, z ) d v 2 f ( x, y, z ) d v
1
(3) 如果 与 关于平面y = x对称，则

f ( x, y, z ) d v
性质 6 设M、m 分别是f(x,y,z)在闭区域 上的最大值和最小值， V为 的体积，则有
mV f ( x, y, z ) d v MV

性质7 （积分中值定理） 设函数f(x, y, z)在闭区域 上连续，V为 的体积，则在
上至少存在一点 (x ,h , z ) 使得下式成立：
f ( x, y, z) d v f (x ,h, z )V

有关三重积分的对称性应用 设 为空间有界比区域，f (x, y, z)在 上连续. (1) 如果 关于xOy(或xOz或yOz) 对称，且f (x, y, z)关于z(或y 或x)为奇函数，则