下载文档原格式
《洛伦兹力》讲义一、什么是洛伦兹力在物理学中，当带电粒子在磁场中运动时，会受到一种力的作用，这种力被称为洛伦兹力。
洛伦兹力是由荷兰物理学家亨德里克·安东·洛伦兹首先提出的。
要理解洛伦兹力，我们先来看看带电粒子的运动。
带电粒子可以是电子、质子等，它们带有一定的电荷量。
当这些带电粒子在没有磁场的情况下做直线运动时，它们遵循牛顿运动定律。
然而，当存在磁场时，情况就变得复杂了。
磁场是一种特殊的物质，它具有能量和动量。
带电粒子在磁场中运动时，会与磁场发生相互作用，从而受到洛伦兹力的影响。
洛伦兹力的大小与带电粒子的电荷量、速度以及磁场的磁感应强度有关。
具体来说，洛伦兹力的大小可以用公式 F ＝qvBsinθ 来表示，其中 F 是洛伦兹力的大小，q 是带电粒子的电荷量，v 是带电粒子的速度，B 是磁场的磁感应强度，θ 是速度方向与磁感应强度方向的夹角。
从这个公式可以看出，如果带电粒子的运动方向与磁场方向平行（即θ ＝ 0 或 180°），那么洛伦兹力为零；只有当带电粒子的运动方向与磁场方向不平行时，才会受到洛伦兹力的作用。
二、洛伦兹力的方向洛伦兹力的方向可以用左手定则来判断。
左手定则的具体方法是：伸出左手，让磁感线垂直穿过手心，四指指向正电荷运动的方向（或者负电荷运动的反方向），那么大拇指所指的方向就是洛伦兹力的方向。
需要注意的是，洛伦兹力的方向始终与带电粒子的运动方向垂直，所以洛伦兹力永远不做功。
这是因为做功的条件是力在力的方向上有位移，而洛伦兹力与运动方向垂直，在运动方向上没有分力，也就不会做功。
举个例子，如果一个带正电的粒子以速度 v 向右运动，磁场方向垂直纸面向里，那么根据左手定则，洛伦兹力的方向向上。
三、洛伦兹力与电场力的区别在研究带电粒子的运动时，我们经常会遇到洛伦兹力和电场力。
虽然它们都是对带电粒子的作用力，但它们有很多不同之处。
首先，产生的原因不同。
电场力是由电场对带电粒子的作用产生的，只要带电粒子处于电场中，就会受到电场力的作用。
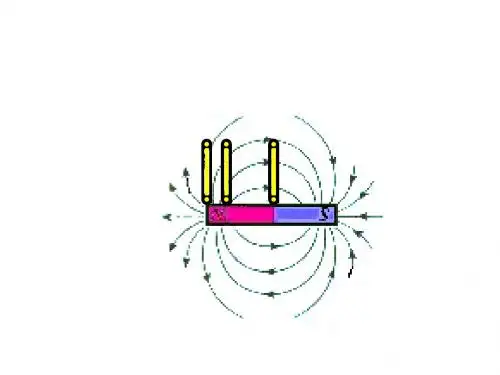
洛伦兹力的微观解释（原创版）目录一、洛伦兹力的概念及公式二、洛伦兹力的微观解释1.电荷在电场中的受力2.电荷在磁场中的受力3.洛伦兹力的微观本质正文一、洛伦兹力的概念及公式洛伦兹力，又称为洛伦兹磁力，是由荷兰物理学家洛伦兹（Hendrik Antoon Lorentz）在 19 世纪末 20 世纪初提出的一种力。
洛伦兹力是描述电荷在电磁场中受到的力的公式，该公式为：F = q(E + v x B)。
其中，F 表示洛伦兹力，q 表示电荷量，E 表示电场强度，v 表示电荷的速度，B 表示磁场强度，x 表示叉乘符号。
二、洛伦兹力的微观解释1.电荷在电场中的受力当电荷处在电场中时，它会受到电场力。
根据库仑定律，电场力 F_E = qE，其中 q 为电荷量，E 为电场强度。
电荷在电场中的受力与电荷的电量和电场强度成正比。
2.电荷在磁场中的受力当电荷处在磁场中时，它会受到磁场力。
根据安培环路定律，磁场力F_B = qvB，其中 q 为电荷量，v 为电荷的速度，B 为磁场强度。
电荷在磁场中的受力与电荷的电量、速度和磁场强度成正比。
3.洛伦兹力的微观本质洛伦兹力实际上是电荷在电场和磁场共同作用下所受到的力。
从微观角度来看，洛伦兹力可以解释为电荷在磁场中受到的力是由于磁场对电荷的运动产生了影响，使得电荷的运动轨迹发生了偏转。
这种偏转现象在电子显微镜中尤为明显，电子在磁场中受到洛伦兹力作用，从而在磁场中形成特定的轨迹。
综上所述，洛伦兹力是一种描述电荷在电磁场中受到的力的公式。
电荷在电场中的受力与电荷的电量和电场强度成正比，电荷在磁场中的受力与电荷的电量、速度和磁场强度成正比。
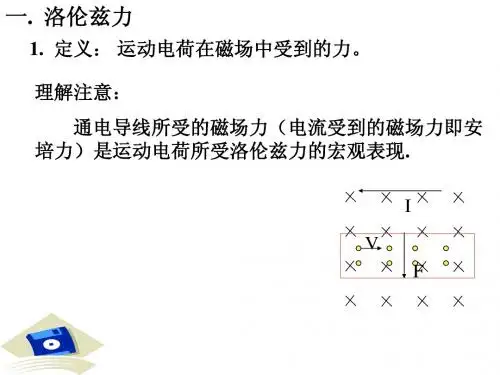
1.洛伦兹力运动电荷在磁场中受到的磁场力叫洛伦兹力，它是安培力的微观表现。
计算公式的推导：如图所示，整个导线受到的磁场力（安培力）为F 安=BIL ；其中I=nesv ；设导线中共有N 个自由电子N=nsL ；每个电子受的磁场力为F ，则F 安=NF 。
由以上四式可得F=qvB 。
条件是v 与B 垂直。
当v 与B 成θ角时，F=qvB sin θ。
2.洛伦兹力方向的判定在用左手定则时，四指必须指电流方向（不是速度方向），即正电荷定向移动的方向；对负电荷，四指应指负电荷定向移动方向的反方向。
3.洛伦兹力大小的计算带电粒子在匀强磁场中仅受洛伦兹力而做匀速圆周运动时，洛伦兹力充当向心力，由此可以推导出该圆周运动的半径公式和周期公式： Bqm T Bqmv r π2,==4.带电粒子在匀强磁场中的偏转 ⑴穿过矩形磁场区。
一定要先画好辅助线（半径、速度及延长线）。
偏转角由sin θ=L /R 求出。
侧移由R 2=L 2-(R-y )2解出。
经历时间由Bqm t θ=得出。
注意，这里射出速度的反向延长线与初速度延长线的交点不再是宽度线段的中点，这点与带电粒子在匀强电场中的偏转结论不同！⑵穿过圆形磁场区。
画好辅助线（半径、速度、轨迹圆的圆心、连心线）。
偏角可由Rr =2tan θ求出。
经历时间由Bqm tθ=得出。
注意：由对称性，射出线的反向延长线必过磁场圆的圆心。
1：如图直线MN 上方有磁感应强度为B 的匀强磁场。
正、负电子同时从同一点O 以与MN 成30°角的同样速度v 射入磁场（电子质量为m ，电荷为e ），它们从磁场中射出时相距多远？射出的时间差是多少？ 解：正负电子的半径和周期是相同的。
只是偏转方向相反。
先确定圆心，画出半径，由对称性知：射入、射出点和圆心恰好组成正三角形。
所以两个射出点相距2r ，由图还看出经历时间相差2T /3。
答案为射出点相距Bemv s2=，时间差为Bqm t 34π=∆。
第II 卷（非选择题）
请点击修改第II 卷的文字说明
1．（8分）如图所示为一速度选择器，板间存在方向互相垂直的匀强电场和磁场。
现有速率不同的电子从A 点沿直线AB 射入板间。
平行板间的电压为300 V ，间距为5 cm ，垂直纸面的匀强磁场的磁感应强度为0.06 T ，问：
(1)匀强磁场的方向指向纸面里还是向外？
(2)能沿直线通过该速度选择器的电子的速率？
【答案】(1) 垂直于纸面向里(2) 105m/s
【解析】
试题分析：(1)由于电子所受到的电场力向上，由平衡知，洛伦兹力向下，由左手定则判断出 B 的方向垂直于纸面向里（2分）
(2)电子受到的洛伦兹力为：F B =evB ，它的大小与电子速率v 有关，只有那些速率的大小刚好使得洛伦兹力与电场力相平衡的电子，才可沿直线KA 通过小孔S
据题意，能够通过小孔的电子，其速率满足下式：evB=eE(2分) 解得：E v B
=
（1分） 又因为U E d
=（2分） 所以U v dB =得v=105m/s （1分） 考点：左手定则、速度选择器、物体平衡、洛伦兹力、电场力
2．（16分）如图所示，在磁感应强度为B 的水平匀强磁场中，有一足够长的绝缘细棒OO′在竖直平面内垂直于磁场方向放置，细棒与水平面夹角为α。
一质量为m 、带电荷量为＋q 的圆环A 套在OO′棒上，圆环与棒间的动摩擦因数为μ，且μ<tan α，现让圆环A 由静止开始下滑，试问圆环在下滑过程中：
（1）圆环A 的最大加速度为多大？获得最大加速度时的速度为多大？
（2）圆环A 能够达到的最大速度为多大？
【答案】（1）m a gsin α＝ 1v mgcos qB
α=
（2）(sin cos )m mg q v B αμαμ+＝ 【解析】
B
试题分析：：(1)由于tan μα<，即sin cos mg mg θμθ>所以环将由静止开始沿棒下滑。
环A 沿棒运动的速度为1v 时，受到重力mg 、洛伦兹力1qv B 、杆的弹力1N 和摩擦力11f N μ＝。
根据牛顿第二定律，对圆环A 受力分析有
沿棒的方向：1mgsin f ma α－＝（2分）
垂直棒的方向：11N qv B mgcos α＋＝（2分）
所以当10f ＝ (即10N ＝)时
a 有最大值m a ，且m a gsin α＝
此时1qv B mgcos α＝（2分） 解得：1v mgcos qB
α=。
（2分） (2)设当环A 的速度达到最大值m v 时，环受杆的弹力为2N ，摩擦力为22f N μ＝。
此时应有0a ＝，即2mgsin f α＝（3分）
在垂直杆方向上
2m N mgcos qv B α＋＝ （3分） 解得：(sin cos )m mg q v B
αμαμ+＝（2分） 考点：洛伦兹力 牛顿第二定律
3．如图所示，质量为m 的小球带有电量q 的正电荷，中间有一孔套在足够长的绝缘杆上，杆与水平成α角，与球的摩擦系数为μ。
此装置放在沿水平方向磁感应强度为B 的匀强磁场之中，从高处将小球无初速释放，小球下滑过程中加速度的最大值是多少？小球运动速度的最大值是多少？ 【答案】sin
m a g θ= sin cos m mg v qB θθμ⎛⎫=+ ⎪⎝⎭
【解析】
试题分析：将小球由静止开始释放，小球受到重力、垂直于杆向上的洛伦兹力、垂直于
杆的支持力和滑动摩擦力．开始阶段，洛伦兹力小于重力垂直杆向下的分力，杆对小球的支持力垂直杆向上，受力如图所示．
由牛顿第二定律有：
垂直杆方向：cos 0N mg f θ-+=洛
沿杆方向：mgsin f ma θ-=
又f qvB =洛 f N μ=
小球向下做加速运动，洛伦兹力逐渐增大，支持力和滑动摩擦力逐渐减小，合力增大，加速度增大，当洛伦兹力等于重力垂直杆向下的分力时，支持力和摩擦力为零，合力最大，加速度最大，则有sin m a g θ=．
此后，小球速度继续增大，当洛伦兹力大于重力垂直杆的分力时，杆对小球的支持力方向变为垂直于杆向下，受力情况如图所示，由牛顿第二定律有：
垂直杆方向：cos 0f N mg θ--=洛
沿杆方向：mgsin f ma θ-=
又f qvB =洛 f N μ= 可解得：sin cos qvB a g g m θμθ⎛⎫=-- ⎪⎝⎭
随着速度增大，滑动摩擦力增大，合力减小，加速度减小，当加速度减小到零，小球做匀速直线运动，速度达到最大，于是可得： sin cos 0m qv B g g m θμθ⎛⎫--= ⎪⎝⎭
解得：sin cos m mg v qB θθμ⎛⎫=+ ⎪⎝⎭
考点：本题考查牛顿第二定律的理解和应用、力的合成与分解的运用、洛仑兹力及左手定则，意在考查考生对带电物体在磁场中运动的受力分析和运动情况分析．
4．如图所示，质量m ＝0.1g 的小物块，带有5×10-4C 的电荷，放在倾角为30°的光滑
绝缘斜面上，整个斜面置于B=0.5T 的匀强磁场中，磁场方向垂直纸面指向纸里，物块由静止开始下滑，滑到某一位置时，开始离开斜面，求：
（1）物块带什么电？
（2）物块离开斜面时速度多大？
（3）斜面至少有多长？
【答案】（1）物体带负电（2）物体离开斜面时的速度为/s （3）斜面至少1.2 m
【解析】
试题分析：（1）带电滑块在滑至某一位置时，由于在安培力的作用下，要离开斜面．根据磁场方向结合左手定则可得带电粒子的电性．
（2）由于斜面光滑，所以小滑块在没有离开斜面之前一直做匀加速直线运动．借助于洛伦兹力公式可求出恰好离开时的速度大小．
（3）由运动学公式来算出匀加速运动的时间．由位移与时间关系可求出位移大小． 解：（1）由题意可知：小滑块受到的安培力垂直斜面向上．
根据左手定则可得：小滑块带负电．
（2）当物体离开斜面时，弹力为零，
因此有：cos30qvB mg =︒，
故cos30/s mg v qB
︒==． （3）由于斜面光滑，物体在离开斜面之前一直做匀加速直线运动，
由牛顿第二定律得：mgsin30°=ma，
由匀变速直线运的速度位移公式得：v 2=2ax ，
解得：x=1.2m ．
考点：洛仑兹力；力的合成与分解的运用。
