磁场---洛伦兹力基础计算

洛伦兹力与电磁感应的原理电磁感应和洛伦兹力是电磁学中重要的概念和原理。

它们描述了电流和磁场之间的相互作用。

本文将探讨洛伦兹力和电磁感应的原理，并探讨它们在实际应用中的重要性。

一、洛伦兹力的原理洛伦兹力是由运动带电粒子在磁场中受到的力。

根据洛伦兹力的原理，当一个运动带电粒子穿过一个磁场时，它将受到一定方向和大小的力。

该力的大小与带电粒子的电荷量、速度以及磁场的大小和方向有关。

洛伦兹力的公式可以表示为：F = q(v × B)其中，F表示洛伦兹力，q表示带电粒子的电荷量，v表示带电粒子的速度，B表示磁场的大小和方向，(v × B)表示矢量积。

根据该公式，洛伦兹力垂直于带电粒子的速度和磁场的平面，并遵循右手定则。

具体而言，当右手的拇指指向带电粒子的速度方向，四指指向磁场方向时，手掌的方向即为洛伦兹力的方向。

洛伦兹力的概念和原理在电磁学领域的应用非常广泛。

例如，在粒子加速器中，科学家利用洛伦兹力将带电粒子加速到极高的速度，用于核物理研究。

此外，洛伦兹力还解释了许多电磁现象，如荷质比实验和霍尔效应等。

二、电磁感应的原理电磁感应是指当导线中的磁通量发生变化时，在导线两端会产生感应电动势。

根据法拉第电磁感应定律，当导线中的磁通量发生变化时，感应电动势的大小与磁通量的变化率成正比。

电磁感应的原理可以通过以下公式表示：ε = -N(dΦ/dt)其中，ε表示感应电动势，N表示线圈的匝数，(dΦ/dt)表示磁通量的变化率。

根据该公式，感应电动势的大小与线圈的匝数和磁通量的变化率有关。

当磁通量的变化率较大时，感应电动势也会增大。

电磁感应广泛应用于发电、变压器和感应加热等领域。

在发电中，利用电磁感应原理，通过旋转磁场和线圈之间的相互作用，将机械能转换为电能。

变压器则利用电磁感应将高压电能转换为低压电能。

此外，感应加热通过电磁感应的原理，将电能转化为热能，用于高效加热。

三、洛伦兹力与电磁感应的关系洛伦兹力和电磁感应是相互关联的。

【问题导思】 1．电荷运动方向和磁场方向一定垂直吗？洛伦兹力方向 与电荷运动方向一定垂直呢？ 2．洛伦兹力对运动电荷做功吗？ 3．电荷只在洛伦兹力作用下运动时，速度大小改变吗？
1．决定洛伦兹力方向的因素有三个：电荷的电性(正、 负)，速度方向、磁感应强度的方向．当电性一定时，其他两 个因素决定洛伦兹力的方向，如果只让一个因素相反，则洛 伦兹力方向必定相反；如果同时让两个因素相反，则洛伦兹 力方向将不变．
A．F、B 、v 三者必定均保持垂直 B．F 必定垂直于 B、v，但 B 不一定垂直于 v C．B 必定垂直于 F，但 F 不一定垂直于 v D．v 必定垂直于 F、B，但 F 不一定垂直于 B 【解析】 由左手定则知 F⊥B，F⊥v，但 v 与 B 不一 定垂直，故 B 正确，其余都错． 【答案】 B
2．思考判断 (1)由于电荷有“正、负”之分，故四指指向应为正电荷 运动的方向或负电荷运动的反方向，即等效电流的方向．(√) (2)洛伦兹力始终与带电粒子的运动方向垂直，故洛伦兹 力永远不做功．(√) (3)安培力和洛伦兹力是性质不同的两种力．(×)
3．探究交流 电荷在电场中一定受电场力作用，想一想，电荷在磁场 中也一定受洛伦兹力作用吗？ 【提示】 不一定，因为如果电荷相对于磁场静止(v＝ 0)或电荷的运动方向与磁场方向平行(v∥B)，电荷在磁场中 都不会受洛伦兹力的作用．
图 3－4－1
【解析】 (1)因 v⊥B，所以 F＝qvB，方向与 v 垂直斜 向上．
(2)v 与 B 夹角为 30°，取 v 与 B 垂直的分量， 故 F＝qvBsin 30°＝12qvB，方向垂直纸面向里． (3)由于 v 与 B 平行，所以不受洛伦兹力． (4)v 与 B 垂直，故 F＝qvB，方向与 v 垂直斜向上．

据题意，小球P在球面上做水平的匀速圆周运动 在球面上做水平的匀速圆周运动, 解： 据题意，小球 在球面上做水平的匀速圆周运动 该圆周的圆心为O' 受到向下的重力mg、 该圆周的圆心为 。P受到向下的重力 、球面对它 受到向下的重力 方向的支持力N和磁场的洛仑兹力 f＝qvB 沿OP方向的支持力 和磁场的洛仑兹力 方向的支持力 和磁场的洛仑兹力f ＝ 式中v为小球运动的速率， 的方向指向O′, 式中 为小球运动的速率，洛仑兹力 f 的方向指向 为小球运动的速率 根据牛顿第二定律： 根据牛顿第二定律：
2m B≥ q g R cosθ
可见，为了使小球能够在该圆周上运动， 可见，为了使小球能够在该圆周上运动，磁感应强度 大小的最小值为
Bmin 2m = q g R cosθ
此时，带电小球做匀速圆周运动的速率为n R sinθ
v= 2a = 2m
N cosθ mg = 0
v2 f N sinθ = m R sinθ 由前面三式得： 由前面三式得： qBR sinθ gR sin2 θ v2 v+ =0 m cosθ
N P mg f R θ O O'
由于v是实数，必须满足： 由于 是实数，必须满足： 是实数 qBR sinθ 2 4 gR sin2 θ =( ) ≥0 m cosθ 由此得： 由此得：
若小球带负电， 解： 若小球带负电，带电小球受到的洛仑兹力向 试管底，不能从试管口处飞出， 错 试管底，不能从试管口处飞出，A错。 洛仑兹力与运动方向垂直，不做功， 错 洛仑兹力与运动方向垂直，不做功，C错。 小球带正电，受到洛仑兹向试管口作匀加速运动 小球带正电，受到洛仑兹向试管口作匀加速运动, 同时随试管向右匀速运动，合运动的轨迹是一条 同时随试管向右匀速运动， 抛物线， 正确 正确。 抛物线，B正确。 小球受到洛仑兹向试管口作匀加速 运动时，又受到洛仑兹力， 运动时，又受到洛仑兹力，方向向 且逐渐增大， 左，且逐渐增大，所以维持试管匀 速运动的拉力F应逐渐增大 正确. 应逐渐增大,D正确 速运动的拉力 应逐渐增大 正确

洛伦兹力与磁场强度的计算洛伦兹力和磁场强度是物理学中一对重要的概念，它们在电磁现象的研究中起着关键作用。

洛伦兹力是指当带电粒子在磁场中运动时所受到的力，而磁场强度则是描述磁场的物理量。

本文将介绍洛伦兹力和磁场强度的概念以及它们的计算方法。

1. 洛伦兹力的概念洛伦兹力是由荷质比不为零的带电粒子在磁场中受到的力。

根据洛伦兹力的定义，可以得出洛伦兹力与以下因素有关：- 带电粒子的电荷量（q）- 带电粒子的速度（v）- 磁场强度（B）洛伦兹力的大小可以用以下公式计算：F = qvBsinθ其中，F表示洛伦兹力的大小，q表示带电粒子的电荷量，v表示带电粒子的速度，B表示磁场强度，θ表示带电粒子速度方向与磁场强度方向之间的夹角。

2. 磁场强度的概念磁场强度是描述一个磁场的物理量，通常用字母B表示。

磁场强度的单位是特斯拉(T)。

磁场强度可以用以下公式计算：B = μ₀I/ (2πr)其中，B表示磁场强度，μ₀表示真空中的磁导率，I表示电流的大小，r表示距离电流源的距离。

3. 洛伦兹力和磁场强度的计算实例假设有一根直导线，通电电流为I，长度为L，位于距离导线r处的点P处。

我们需要计算点P处的磁场强度和洛伦兹力。

首先，根据上述公式，我们可以计算出点P处的磁场强度B：B = μ₀I/ (2πr)接下来，我们考虑将一个带电粒子放置在点P处，该带电粒子的电荷量为q，速度为v。

带电粒子所受的洛伦兹力可以通过以下公式计算：F = qvBsinθ在这个例子中，θ是指带电粒子速度方向与磁场强度方向之间的夹角。

根据具体的情况，θ可能需要通过几何关系来确定。

4. 总结本文介绍了洛伦兹力和磁场强度的概念以及它们的计算方法。

洛伦兹力描述了带电粒子在磁场中受到的力，而磁场强度描述了磁场的物理量。

洛伦兹力和磁场强度的计算公式可以帮助我们理解和分析电磁现象。

在实际应用中，了解这些概念和计算方法对于解决相关问题和设计电磁设备非常重要。

【总字数：433】。

磁感应强度（磁场强度）与相关公式磁感应强度（或称为磁场强度）是描述磁场的物理量，表示磁场对单位电流所产生的力的大小。

以下是与磁感应强度相关的公式的解释：1. 洛伦兹力公式洛伦兹力公式描述了一个带电粒子在磁场中受到的力的大小。

该公式如下所示：F = q(v x B)其中， - F 是洛伦兹力（单位：牛顿，N） - q 是带电粒子的电荷量（单位：库仑，C） - v 是带电粒子的速度（单位：米/秒，m/s） - B 是磁感应强度（单位：特斯拉，T）这个公式表明，当一个带电粒子以速度v在磁感应强度为B的磁场中运动时，它将受到一个与其速度和磁场方向垂直的力。

这个力的大小与电荷量、速度以及磁感应强度有关。

2. 磁感应强度与磁场密度的关系磁感应强度B与磁场密度（磁感应密度）Bd 的关系可以通过以下公式描述：B = μ0 * Bd其中， - B 是磁感应强度（单位：特斯拉，T） - Bd 是磁场的磁场密度（单位：特斯拉，T） - μ0 是真空中的磁导率（单位：特斯拉·米/安培，T·m/A）磁感应强度与磁场密度之间的关系表明，它们是成正比的。

真空中的磁导率μ0是一个常量，它决定了磁场强度与磁场密度之间的比例关系。

3. 磁场中的安培环路定理安培环路定理描述了磁场中闭合回路上磁场强度积分的关系。

安培环路定理可以用以下公式表示：∮B · dl = μ0 * I其中， - ∮B · dl 表示沿闭合回路的磁感应强度（单位：特斯拉·米，T·m） - μ0 是真空中的磁导率（单位：特斯拉·米/安培，T·m/A） - I 是通过闭合回路的电流（单位：安培，A）安培环路定理表明，磁感应强度沿着闭合回路的积分与通过该回路的电流成正比。

磁导率μ0是一个常量，它决定了磁感应强度与电流之间的比例关系。

4. 磁感应强度与磁通量的关系磁感应强度B与磁通量Φ的关系可以通过以下公式描述：Φ = B · A其中，- Φ 是磁通量（单位：韦伯，Wb）- B 是磁感应强度（单位：特斯拉，T） - A 是垂直于磁感应强度的面积（单位：平方米，m^2）磁感应强度与磁通量之间的关系表明，它们是成正比的。

洛伦兹力和磁场力
洛伦兹力是指当带电粒子运动时，在磁场中所受到的力。

这种力量是由美国物理学家洛伦兹第一次提出的，他在研究电磁现象时发现了这一现象，从而奠定了电磁学的基础。

磁场力是描述磁场对带电粒子施加力的力量。

磁场力与洛伦兹力密切相关，在许多物理和工程应用中起着重要作用。

洛伦兹力和磁场力的本质相同，都是描述电磁交互作用引起的力。

它们的计算公式是相似的，由洛伦兹力定律给出：
F = q(v × B)
其中，F为洛伦兹力或磁场力，q为带电粒子的电荷量，v为带电粒子的速度矢量，B为磁场的磁感应强度矢量。

这个公式表明，洛伦兹力或磁场力的大小与带电粒子的电荷量、速度以及磁场的强度有关。

洛伦兹力和磁场力在许多领域都有广泛的应用。

在物理学中，它们用于解释和研究电磁现象，如电磁感应、电磁波的传播等。

在工程学中，它们被用于设计和控制电磁设备，如电动机、发电机等。

洛伦兹力和磁场力在实际应用中具有重要意义。

例如，在磁共振成像（MRI）技术中，通过利用洛伦兹力和磁场力，可实现对人体组织的成像和诊断。

另外，磁悬浮列车也是基于磁场力的原理，通过控制磁场力的大小和方向，使列车脱离轨道悬浮运行，从而达到高速、低能耗的效果。

总结来说，洛伦兹力和磁场力是研究电磁现象和应用电磁力的重要概念。

它们的计算公式相似，都基于洛伦兹力定律。

在物理学和工程学中具有广泛的应用，对于我们理解和应用电磁力具有重要意义。

磁场中的洛伦兹力计算方法在物理学中，磁场中的洛伦兹力是一种基本的力，它描述了电荷在磁场中所受到的作用力。

在这篇文章中，我们将介绍磁场中洛伦兹力的计算方法，并探讨其在物理学和工程学中的应用。

一、洛伦兹力的定义洛伦兹力是描述电荷在磁场中受力的一种力，其大小和方向与电荷、磁场和电荷的速度有关。

根据洛伦兹力的定义，我们可以得到如下的洛伦兹力公式：F = q * (v × B)其中，F表示洛伦兹力的大小，q为电荷的大小，v为电荷的速度，B为磁场的磁感应强度。

而符号“×”表示的是向量的叉乘，它决定了洛伦兹力的方向。

二、洛伦兹力的计算方法洛伦兹力的计算方法主要分为两个步骤：首先确定磁场在给定位置的磁感应强度B，然后将电荷的大小q、速度v和磁感应强度B代入洛伦兹力公式进行运算。

1. 确定磁感应强度B在实际计算中，磁感应强度B可以通过使用磁感应仪器进行测量或者通过已知的磁场分布进行计算获得。

如果有多个磁场源，则需要将各个磁场的贡献进行叠加，得到总的磁感应强度。

2. 计算洛伦兹力一旦确定了磁感应强度B，我们可以将电荷的大小q、速度v和磁感应强度B代入洛伦兹力公式进行计算。

需要注意的是，这里的速度向量v必须是电荷运动的瞬时速度，而不是平均速度。

计算得到的洛伦兹力是一个矢量，其方向垂直于速度向量和磁感应强度的叉乘，符合右手法则。

三、洛伦兹力的应用洛伦兹力在物理学和工程学中有着广泛的应用。

以下是一些常见的应用领域：1. 电动机和发电机电动机和发电机是利用洛伦兹力工作的重要设备。

通过在磁场中通电导体中产生的洛伦兹力，可以实现电能与机械能的转换。

这种原理被广泛应用于各种电动设备和发电设备中。

2. 磁控管和磁控阀磁控管和磁控阀是一种功能特殊的电子元器件，它们利用洛伦兹力来实现对粒子流的控制。

通过调节磁场的磁感应强度，可以精确地控制粒子在空间中的移动轨迹，从而实现各种功能，如流量调节和粒子分选。

3. 磁共振成像磁共振成像（MRI）是一种利用洛伦兹力原理的影像技术，常用于医学诊断和科学研究中。

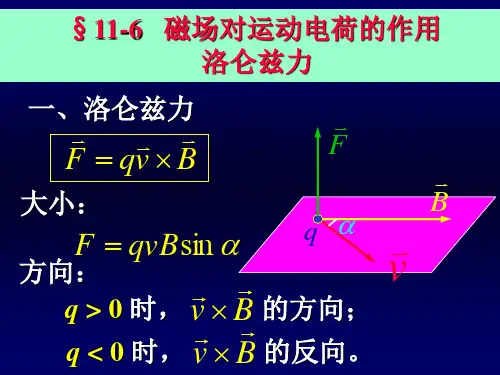
洛仑兹力[P1]洛仑兹力：运动电荷受到的磁场的作用力，叫做洛仑兹力．（1）洛仑兹力大小： f = q v B sin θ f = B q V （当B ⊥V 时）， 当电荷静止或运动电荷的速度方向跟磁感强度的方向平行时，电荷都不受洛仑兹力。

（2）洛仑兹力的方向——由左手定则判断。

注意：①洛仑兹力一定垂直于B 和V 所决定的平面.②四指的指向是正电荷的运动方向或负电荷运动的反方向；（3）特性：洛仑兹力对电荷不做功，它只改变运动电荷的速度方向，不改变速度的大小。

（4）洛伦兹力和安培力的关系：洛伦兹力是安培力的微观表现。

[P2]洛伦兹力计算公式的推导：如图所示，整个导线受到的磁场力（安培力）为F 安=BIL ；其中I=nesv ；设导线中共有N 个自由电子N=nsL ；每个电子受的磁场力为F ，则F 安=NF 。

由以上四式得F=qvB 。

条件是v 与B 垂直。

当v 与B 成θ角时，F=qvB sin θ。

[P3]带电粒子在磁场中的圆周运动：若带电粒子速度方向与磁场方向平行(相同或相反)，带电粒子以不变的速度做匀速直线运动．当带电粒子速度方向与磁场垂直时，带电粒子在垂直于磁感应线的平面内做匀速圆周运动．带电粒子在匀强磁场中仅受洛伦兹力而做匀速圆周运动时，洛仑兹力充当向心力：rmv qvB 2=， 由此可以推导出该圆周运动的半径公式和周期公式：Bqm T ,Bq mv r π2== m )qBR (mv E k 22122==动能[P4]2007年上海卷）在磁感应强度B 的匀强磁场中，垂直于磁场放入一段通电导线。

若任意时刻该导线中有N 个以速度v 做定向移动的电荷，每个电荷的电量为q 。

则每个电荷所受的洛伦兹力f ＝ q v B __，该段导线所受的安培力为F ＝ N q v B ___。

[P5]2007高考理综北京卷）图1是电子射线管示意图.接通电源后，电子射线由阴极沿x 轴方向射出,在荧光屏上会看到一条亮线.要使荧光屏上的亮线向下（z 轴负方向）偏转，在下列措施中可采用的是____B______。

实验结论
通过实验验证了洛伦兹力公式，证明了磁场对运动电荷存在作用力，为电磁学理论提供了实验支持。
实验意义
洛伦兹力实验对于理解电磁场与带电粒子的相互作用具有重要意义，有助于深入探究电磁现象的本质 和规律。此外，该实验还可应用于粒子加速器、电子显微镜等领域，为相关技术发展提供理论支持和 实践指导。
பைடு நூலகம் 05
偏转的方向取决于电荷的电性 （正或负）和磁场的强度。
磁场对带电粒子的作用力还与 其运动方向有关，当粒子垂直 于磁场方向运动时，受到的洛 伦兹力最大。
洛伦兹力与磁场强度的关系
洛伦兹力的大小与磁场的强度成正比， 即磁场越强，洛伦兹力越大。
洛伦兹力的方向由右手定则确定，即伸 开右手，让拇指与其余四指垂直，并使 拇指指向正电荷的运动方向，然后让磁 感线穿过手心，四指指向就是洛伦兹力
洛伦兹力与带电粒子所受的电场力和重力相比， 在一些特定条件下可以忽略不计。
在研究带电粒子在磁场中的运动时，还需考虑其 他物理量如电场、重力场等的影响。
洛伦兹力在科技领域的应用
在磁约束聚变反应中，洛伦兹力用于控制带电粒子的运动轨迹，从而实现 核聚变反应。
在电子显微镜中，洛伦兹力用于操纵电子束的运动，从而提高成像质量。
粒子加速器
洛伦兹力用于加速带电粒子，如电子、质子等，以研究基本粒子和物质结构。
同步辐射光源
在粒子加速器中，利用洛伦兹力产生的同步辐射作为光源，可用于材料科学、 生物学等领域的研究。
洛伦兹力在核聚变中的应用
核聚变反应控制
在核聚变反应中，利用强磁场和高速运动的带电粒子之间的洛伦兹力来控制反应 过程，实现可控热核聚变。
洛伦兹力的方向
• 根据左手定则判断：将左手掌摊平，让磁感线穿过手掌心，四 指指向正电荷的运动方向或负电荷运动的反方向，大拇指所指 方向即为洛伦兹力的方向。

磁场中的洛伦兹力和磁感应强度磁场是环绕着电流或磁体的区域，其中存在着洛伦兹力和磁感应强度。

洛伦兹力是指电荷在磁场中受到的力，而磁感应强度则是磁场的一种度量。

本文将详细介绍磁场中的洛伦兹力和磁感应强度的概念、计算方法以及应用。

一、洛伦兹力在磁场中，电荷受到的洛伦兹力与电荷的速度和外磁场之间的相对位置有关。

洛伦兹力的计算公式为F = qvBsinθ，其中F代表力的大小，q代表电荷的电量，v代表电荷的速度，B代表磁感应强度，θ代表电荷速度方向与磁感应强度方向的夹角。

例如，当一个带有电荷量q的电子以速度v在磁感应强度为B的磁场中运动时，洛伦兹力就是F = qvBsinθ。

如果电子的速度方向与磁感应强度的方向垂直，那么洛伦兹力的大小就是F = qvB。

洛伦兹力的方向则由左手定则决定，即当左手的食指指向电子运动的方向，中指指向磁感应强度的方向，那么大拇指的方向就是洛伦兹力的方向。

二、磁感应强度磁感应强度是磁场的一种度量，它可以表示磁场的强弱。

磁感应强度的单位是特斯拉(T)，常用的符号是B。

磁感应强度的计算公式为B= F / (qvsinθ)，其中F代表洛伦兹力的大小，q代表电荷的电量，v代表电荷的速度，θ代表洛伦兹力方向与电荷速度方向的夹角。

在一定条件下，可以通过测量洛伦兹力的大小和电荷的速度以及确定θ的值，来计算磁感应强度。

例如，在一个已知洛伦兹力和电荷速度的实验中，根据洛伦兹力的计算公式F = qvBsinθ，我们可以通过测量F和qvsinθ的值，来计算磁感应强度B的大小。

这种方法被广泛应用于实验室中对磁场的测量。

三、洛伦兹力和磁感应强度的应用洛伦兹力和磁感应强度在生活和科学研究中都具有重要的应用价值。

1. 电机和发电机电机和发电机的原理都是基于洛伦兹力的作用。

电机通过在磁场中通电线圈中产生一个旋转的磁场，使得电流线圈在磁场力的作用下受到力矩而旋转。

而发电机则是通过旋转的磁场感应线圈中产生电流，实现能量的转换。

线圈受的磁力矩最大
M max Bpm
a(b) n
Fab
B
Fcd
BIS a(b)
d (c)
Fab
(2) = 0 时线圈受到的磁力矩为零
----稳定的平衡位置
线圈稍受扰动，就会回到平衡位置。
Fcd d (c) B
a(b) Fab
(3) = 时线圈所受力矩为零
----不稳定的平衡位置 线圈稍受扰动，就会离开平衡位置。
解： 线圈磁矩
pm NISn
1 NI R2n
2
R
I
600 B
n
磁力 矩 M pm B
磁力矩大小为
M pmB sin 600
R
I
600 B
n
1 NIR2B 3 3 NIBR 2
2
24
磁力矩方向竖直向上。
线圈俯视的转动方向为逆时针。
α
线圈从该位置 由60o 减小为 0。
转到平衡位置时， BS
A I2
b
导线右侧磁场方向如图。
导线 AB 所受力：
dFAB BI 2dl
I1
B
a
C
0 2
I1 b
I2dl
各电流元所受安倍
力的方向相同，
dF
A I2
b
FAB
dFAB
0 I1I 2 2
a b
方向向左。
导线 BC 所受力：
r
dFBC BI 2dl
I1
B
a
C
0 2
I1 r
I 2 dr
M pm B
该式只适用于匀强磁场。
例：下列平面线圈与磁感应线平 行，求它所受磁力矩的大小及转动 方向。

么磁场是否对运动电荷也有作用力呢?
荷兰物理学家 洛伦兹 (Lorentz， 1853—1928)
荷兰物理学家，他 是电子论的创始人、相 对论中洛伦兹变换的建 立者，并因在原子物理 中的重要贡献（塞曼效 应）获得第二届（1902 年）诺贝尔物理学奖。 被爱因斯坦称为“我们 时代最伟大，最高尚的 人”。
D．相对于预定点稍向北偏转
人类首次拍到南北极光“同放光彩”奇
景
以正电荷为例
+
+
在太阳创造的诸如光和热等形式的能量中， 有一种能量被称为“太阳风”。这是一束可以 覆盖地球的强大的带电亚原子颗粒流，该太阳 风在地球上空环绕地球流动，以大约每秒400 公里的速度撞击地球磁场，磁场使该颗粒流偏 向地磁极下落，它们与氧和氮的原子碰撞，击 走电子，使之成为激发态的离子，这些离子发 射不同波长的辐射，产生出红、绿或蓝等色的 极光特征色彩，形成极光。在南极地区形成的 叫南极光。在北极地区同样可看到这一现象， 称之为北极光。
洛伦兹力和电场力的区别：
1.受力：电荷在电场中一定受到电场 力的作用，与其运动状态无关；而电 荷在磁场中不一定受到磁场力作用， 只有相对于磁场运动且运动方向与磁 场方向不平行的电荷才受磁场力作用.
2.大小：F电＝qE
F洛=qvBsinθ
3、方向： 电荷所受电场力方向总是平行于电 场方向； 电荷所受磁场力方向总是垂直于磁 场方向，垂直于运动方向。
F洛 qvB
(v垂直B)
问题:若带电粒子不垂直射入磁场 ,粒子受到的洛伦兹力又如何呢?
V2 V1
三、洛伦兹力的大小
当运动电荷的速度v方向与磁感应强 度B方向的夹角为θ，电荷所受的洛伦兹 力大小为
F洛 qvB sin

磁场中的磁感应强度和洛伦兹力的计算磁场是物理学中重要的概念之一，它可以影响周围物体的运动和相互作用。

在磁场中，磁感应强度和洛伦兹力是我们进行相关计算和分析的重要参数。

本文将介绍如何计算磁场中的磁感应强度和洛伦兹力，并且探讨它们的应用。

一、磁感应强度的定义和计算在磁场中，磁感应强度是描述该场强度的物理量，表示磁场对单位磁荷或者电流的作用力。

磁感应强度的单位是特斯拉(Tesla)，常用符号为B。

磁感应强度的计算可以通过以下公式得到：B = μ0 * (H + M)其中，B表示磁感应强度，μ0是真空磁导率，其数值约为4π×10^-7 T·m/A，H代表磁场强度，M表示磁化强度。

二、洛伦兹力的定义和计算洛伦兹力是自然界中与电磁相互作用有关的力之一，它描述了电荷或者电流在磁场中受到的作用力。

洛伦兹力可以通过以下公式计算得到：F = Q * (v × B)其中，F表示洛伦兹力的大小和方向，Q是电荷的大小，v表示电荷的速度，B为磁感应强度的矢量形式。

需要注意的是，当电流通过导线时，洛伦兹力的计算公式可以表示为：F = I * (L × B)其中，F表示洛伦兹力的大小和方向，I是电流的大小，L为电流元素的长度，B表示磁感应强度的矢量形式。

三、磁感应强度和洛伦兹力的应用1. 电磁感应：当变化的磁场穿过一个导线环路时，根据法拉第电磁感应定律，磁感应强度的变化将导致感应电动势的产生。

这个现象在电磁感应、发电和变压器等领域有重要应用。

2. 磁场力场：在磁场中，洛伦兹力对带电粒子施加一个力，可以改变其运动轨迹。

这一特性被广泛应用于粒子加速器、电子显微镜和质子磁共振成像等科学技术领域。

3. 恒定电磁场中的粒子运动：在恒定电磁场中，洛伦兹力会对带电粒子产生一个力，使其在磁场中绕着磁力线做圆周运动。

这个现象在质谱仪、电子注入离子阱和磁控火箭等应用中发挥重要作用。

4. 电磁感应传感器：利用变化的磁场对感应线圈产生感应电动势，可以制作磁场传感器，用于检测磁场的强度和方向，广泛应用于地球磁场探测、导航和地震预警领域。

磁场中的洛伦兹力计算在物理学中，洛伦兹力是指一个带电粒子在磁场中所受到的力。

这个力是由洛伦兹定律所描述的，洛伦兹力公式可以用来计算磁场中带电粒子所受的力。

洛伦兹力的计算公式为：F = q(v × B)其中，F表示洛伦兹力，q表示带电粒子的电荷量，v表示带电粒子的速度，B表示磁场。

在上述公式中，叉乘（×）的结果是一个向量，它垂直于带电粒子的速度和磁场的平面，并且方向通过右手规则确定。

如果带电粒子的速度和磁场方向垂直，那么洛伦兹力的大小可以通过以下公式计算：F = qvB如果带电粒子的速度和磁场方向平行或反平行，那么洛伦兹力将为零。

为了更好地理解洛伦兹力的计算，可以通过一个示例来进行说明。

假设有一个带电粒子电荷量为q，速度为v，处于一个磁场B中。

我们可以通过上述公式计算洛伦兹力的大小。

假设带电粒子的速度和磁场方向垂直，则洛伦兹力的大小为：F = qvB在实际应用中，洛伦兹力的计算在许多领域都有重要的应用。

例如，当带电粒子通过磁感应强度为B的磁场时，洛伦兹力可以计算出粒子在磁场中的受力情况。

磁场中的洛伦兹力是电动力学中的一个重要概念，对于研究带电粒子在外部磁场中的运动和相互作用具有重要意义。

此外，洛伦兹力的计算不仅适用于粒子在磁场中的情况，还可以应用于磁场中的导线。

当电流通过导线时，导线中的电荷也会受到洛伦兹力的作用。

利用洛伦兹力的计算公式，可以计算出导线在磁场中所受的力，这在许多电磁应用中具有重要作用。

总结起来，洛伦兹力的计算公式为F = q(v × B)，可以用于计算带电粒子在磁场中所受到的力。

这种力的大小和方向与速度和磁场之间的关系有关。

洛伦兹力的计算在物理学和工程学中具有广泛的应用，对于研究带电粒子在磁场中的运动和相互作用起着关键的作用。

磁场---洛伦兹力根底计算1、〔12分〕下左图中MN表示真空室中垂直于纸面的平板，它的一侧有匀强磁场，磁场方向垂直于纸面向里，磁感应强度大小为B。

一带电粒子从平板上的狭缝O处以垂直于平板的初速v射入磁场区域，最后到达平板上的P点。

B、v以及P到O的距离l，不计重力，求此粒子的电荷q与质量m之比。

2、如以下图，一束电子流以速率v通过一个处于矩形空间的大小为B的匀强磁场，速度方向与磁感线垂直．且平行于矩形空间的其中一边，矩形空间边长为a和a电子刚好从矩形的相对的两个顶点间通过，求：〔1〕电子在磁场中的飞行时间？〔2〕电子的荷质比q/m．3、如以下图，一个电子(电量为e)以速度v垂直射入磁感应强度为B、宽度为d的匀强磁场中，穿出磁场时的速度方向与原来入射方向的夹角是30°，试计算：(1)电子的质量m。

(2)电子穿过磁场的时间t。

4、一宽为L的匀强磁场区域，磁感应强度为B，如以下图，一质量为m、电荷量为－q的粒子以某一速度(方向如以下图)射入磁场。

假设不使粒子从右边界飞出，那么其最大速度应为多大？(不计粒子重力)5、〔12分〕一个质量为m电荷量为q的带电粒子从x轴上的P〔a，0〕点以速度v，沿与x正方向成60°的方向射入第一象限的匀强磁场中，并恰好垂直于y轴射出第一象限，不计重力。

求:〔1〕粒子做圆周运动的半径〔2〕匀强磁场的磁感应强度B6、如以下图，在xoy平面有垂直坐标平面的围足够大的匀强磁场，磁感强度为B，一带正电荷量Q的粒子，质量为ｍ，从Ｏ点以某一初速度垂直射入磁场，其轨迹与x、y轴的交点A、B到O点的距离分别为ａ、ｂ，试求：(1)初速度方向与ｘ轴夹角θ．(2)初速度的大小.7、一电子〔e，m〕以速度ｖ与ｘ轴成30°角垂直射入磁感强度为B的匀强磁场中，经一段时间后，打在ｘ轴上的P点，如以下图，那么P点到O点的距离为多少？电子由O点运动到P点所用的时间为多少？8、如以下图，在x轴上方存在着垂直于纸面向里、磁感应强度为B的匀强磁场。

是一种利用电子替代光学显微镜进行观察和分析微观物体的仪器。在 电子显微镜中，洛伦兹力被用于控制电子束的运动轨迹，从而实现高分辨率和高 放大倍率的观察。
通过精确地控制磁场和电场，洛伦兹力可以引导电子束进行精确的扫描和成像， 从而获得高清晰度的显微图像。这使得科学家能够观察和分析纳米级和亚纳米级 的结构和性质，为材料科学、生物学和医学等领域的研究提供了重要的手段。
磁场对运动电荷的作 用-洛伦兹力
contents
目录
• 洛伦兹力概述 • 磁场对运动电荷的作用 • 洛伦兹力在实际中的应用 • 洛伦兹力的实验验证 • 洛伦兹力的物理意义与局限性
01
洛伦兹力概述
定义与公式
定义
洛伦兹力是磁场对运动电荷的作 用力。
公式
$F = qvBsintheta$，其中$q$是 电荷量，$v$是运动电荷的速度， $B$是磁感应强度，$theta$是速 度与磁感应强度的夹角。
3
当电荷运动方向与磁场成任意角度时，洛伦兹力 的大小可以根据公式$F = qvBsintheta$计算。
02
磁场对运动电荷的作用
磁场对直线运动电荷的作用
总结词
当电荷在磁场中沿直线运动时，洛伦兹力垂直于运动方向和磁场方向，表现为向心力，使电荷做匀速圆周运动。
详细描述
当电荷在磁场中沿直线运动时，洛伦兹力垂直于电荷的运动方向和磁场方向，其大小与电荷的运动速度、磁场强 度以及电荷的电量和质量有关。洛伦兹力的作用使电荷受到向心力的作用，使电荷做匀速圆周运动。
总结词
当带电粒子束在磁场中穿过时，洛伦兹力会使粒子束发生偏 转，形成束流。
详细描述
当带电粒子束在磁场中穿过时，每个粒子都受到洛伦兹力的 作用，使粒子束发生偏转。由于粒子束中粒子的速度和电量 不同，束流在磁场中会发生散射和聚焦，形成特定的束流形 状。

物理洛仑兹力计算公式洛伦兹力计算公式：F=qvBsinθ左手定则：伸出你的左手，让磁感线穿过掌心，四指的方向代表着正电荷运动的方向（负电荷运动的反方向。

）。

大拇指的方向代表着洛伦兹力的方向。

磁场打叉，掌心向外，由于是正电荷，适时的方向与正电荷运动的方向相同。

所以受到洛伦兹力竖直向下。

磁场打点，掌心向里。

四指的方向代表着负电荷运动的反方向。

可以得出洛伦兹力竖直向上。

磁场向左，掌心向右，四指的方向与负电荷运动的反方向相同，得出洛伦兹力竖直向下。

磁场向上，掌心向下。

四指的方向与正电荷运动的方向相同。

得到路人之力竖直向下。

洛伦兹力所有公式洛伦兹力的公式：F=qvBsinθ1、v和B平行的时候洛伦兹力等于0。

2、V和b垂直的时候，洛伦兹力等于qvB。

3、V和b成θ角的时候，F=qvBsinθ洛伦兹力计算公式扩展：洛伦兹力的公式是F=qvBsin0，其中0是v与B的夹角;当v与B的方向垂直时，可以简化为F=qvB;卜面我们从安培力的公式来推导洛伦兹力的公式。

基本物理量中，设通电导体的长度:L，导体棒为圆柱体，横截面积:S，单位体积内的电荷数: n，每个电荷的带电量:q，所有电荷定向移动的速率: v。

由于F安=BIL，l=nqvS，带入可得，F安=qvB(nLS)，N=nls洛伦兹力为安培力平均分配给单个电荷的力，因此F洛=F安/N，带入上式中，我们得到洛伦兹力的物理公式:F洛=qvB。

若v与B间的夹角为0，不难得出F =qvBsin0。

洛伦兹力运动电荷在磁场中所受的力。

它是荷兰物理学家H·A·洛伦兹于1895年建立经典电子论时,作为基本假定而提出的,后被大量实验结果所证实,因此得名。

洛伦兹力更为本质的解释是什么等学了狭义相对论以后，就会明白洛伦兹力的本质了。

推荐题主找本狭义相对论的书看看。

总之，狭义相对论要求洛伦兹力必须存在而且必须是那种形式。

上面几个回答时空弯曲的我不知道是什么意思。

洛伦兹力和广义相对论、时空弯曲没关系, 也不需要用纤维从弯曲之类的东西来解释，那个是完全冗余的数学构造，不是物理实质。