洛伦兹力的一种推导

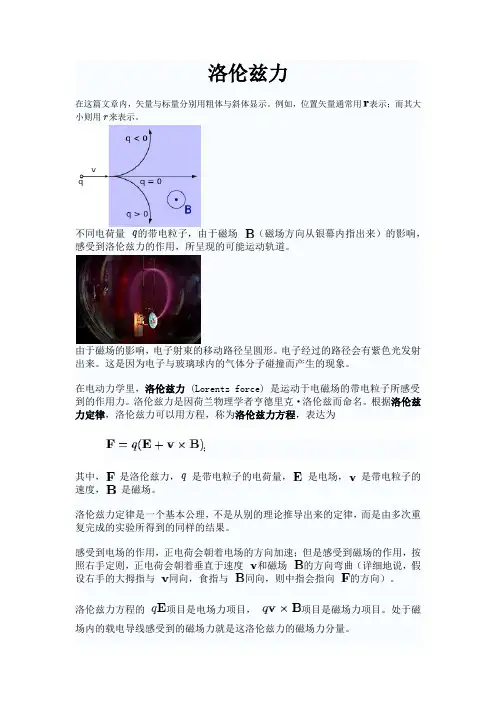
洛伦兹力在这篇文章内，矢量与标量分别用粗体与斜体显示。

例如，位置矢量通常用表示；而其大小则用来表示。

不同电荷量的带电粒子，由于磁场（磁场方向从银幕内指出来）的影响，感受到洛伦兹力的作用，所呈现的可能运动轨道。

由于磁场的影响，电子射束的移动路径呈圆形。

电子经过的路径会有紫色光发射出来。

这是因为电子与玻璃球内的气体分子碰撞而产生的现象。

在电动力学里，洛伦兹力 (Lorentz force) 是运动于电磁场的带电粒子所感受到的作用力。

洛伦兹力是因荷兰物理学者亨德里克·洛伦兹而命名。

根据洛伦兹力定律，洛伦兹力可以用方程，称为洛伦兹力方程，表达为；其中，是洛伦兹力，是带电粒子的电荷量，是电场，是带电粒子的速度，是磁场。

洛伦兹力定律是一个基本公理，不是从别的理论推导出来的定律，而是由多次重复完成的实验所得到的同样的结果。

感受到电场的作用，正电荷会朝着电场的方向加速；但是感受到磁场的作用，按照右手定则，正电荷会朝着垂直于速度和磁场的方向弯曲（详细地说，假设右手的大拇指与同向，食指与同向，则中指会指向的方向）。

洛伦兹力方程的项目是电场力项目，项目是磁场力项目。

处于磁场内的载电导线感受到的磁场力就是这洛伦兹力的磁场力分量。

洛伦兹力方程的积分形式为。

其中，是积分的体积，是电荷密度，是电流密度，是微小体元素。

洛伦兹力密度是单位体积的洛伦兹力，表达为：。

历史亨德里克·洛伦兹1892年，荷兰物理学家亨德里克·洛伦兹提出洛伦兹力的概念。

但是，在洛伦兹之前，就已经有发掘出洛伦兹力方程的形式，特别是在詹姆斯·麦克斯韦的1861 年论文《论物理力线》里的公式 (77)：、、；其中，、、分别为电场的三个分量，是磁导率，、、分别为导电体的移动速度的三个分量，、、分别为磁场强度的三个分量，、、分别为磁矢势的三个分量，是电势。

后来，在他的 1864 年论文《电磁场的动力学理论》里，麦克斯韦将这公式列为麦克斯韦方程组的八个原本方程中的方程(D) :；其中，是速度，是磁场强度，是磁导率，是磁矢势，是电势。

洛伦兹洛伦茨公式推导
基本推导：安培力是洛伦兹力的宏观表现，故从安培力大小公式，可以反推得洛伦兹力公式。

安培力F=BIL，电流I=Q/t，代入上式F=BL(Q/t)=QvB(从宏观到微观)，从微观到宏观，
F=BIL=BnqsvL=NBqv，即F（安培力）=Nf(f是洛伦兹力)。

运动电荷在磁场中所受的力叫做洛伦兹力。

洛伦兹力是因荷兰物理学者亨德里克·洛伦兹而命名。

根据洛伦兹力定律，洛伦兹力可以用方程，称为洛伦兹力方程。

洛伦兹力的方向可用左手定则来判断。

伸开左手，使拇指与其余四个手指垂直，并且都与手掌处于同一水平面，让磁感线从掌心进入，四指指向正电荷运动的方向，拇指指的方向即洛伦兹力力的方向。

公式：F=Bqvsinθ（θ是v和B的夹角）。

安培力与洛伦兹力一、安培力定义：通电导线在磁场中所受的力。

大小：1、磁场与电流垂直时，F=BIL2、磁场与电流平行时，F=03、磁场与电流成b角时，F=BILsin b理解:1、公式适用于匀强磁场,若为非匀强，则需要用到积分。

2、公式中的夹角为磁场与导线的夹角.3、磁场有垂直电流方向的分量才对电流产生力的作用，平行电流方向对电流不产生力的作用。

因此，如果知道一段导线的受力，我们只可以确定磁场垂直电流方向的分量，换句话说,我们只可以确定场强的最小值。

4、对于一段导线有效长度的确定.直导线：本身长度*sin b(磁场与导线的夹角)弯曲导线：在导线所在平面垂直于磁场方向的前提下，有效长度为两端点的连线.5、对于闭合线圈，其有效长度一定为0.因此，对于完全处于匀强磁场中的闭合线圈，其所受的磁场力合力一定为零。

方向：左手定则（判断磁场方向——右手、判断受力方向——左手）同时垂直与电流方向和磁场方向。

注意：不管电流方向与磁场方向是否垂直，安培力方向总垂直与电流方向与磁场方向决定的平面。

二、洛伦兹力定义：运动电荷在磁场中所受的力.大小：1、v//B或v=0时，F=0。

2、v垂直于B时，F=qvb。

3、v与B的夹角为ɑ时，F=Bqvsin ɑ。

4、B、ɑ、v均为粒子运动过程中的瞬时量。

方向：1、使用左手定则进行判定（判断磁场用右手，判断受力用左手）。

2、四指指向一定是正电荷的运动方向，是负电荷的反方向.(四指指向电流方向）。

3、洛伦兹力的方向和电荷运动方向与磁场方向都垂直（不做功）。

理解:1、洛伦兹力与速度成正比，并且与速度的方向有关，同样的速度，垂直磁场入射的时候，洛伦兹力最大。

2、洛伦兹力始终和速度方向垂直,根据W=FSsinɑ，ɑ=90知，W=0.也就是说洛仑兹力始终不做功.3、做功为0，根据功能关系,能量不改变，洛伦兹力不改变速度的大小。

由牛顿第一定律，力可以改变物体运动状态,洛伦兹力改变速度大小。

三、安培力与洛伦兹力的内在关系由安培力F=BIL推导洛伦兹力F=qvB设：导体的横截面积为S，单位体积的电荷数为n，自由电荷的电荷量为q，电荷定向移动的速度大小为v。

洛仑兹力[P1]洛仑兹力：运动电荷受到的磁场的作用力，叫做洛仑兹力．（1）洛仑兹力大小： f = q v B sin θ f = B q V （当B ⊥V 时）， 当电荷静止或运动电荷的速度方向跟磁感强度的方向平行时，电荷都不受洛仑兹力。

（2）洛仑兹力的方向——由左手定则判断。

注意：①洛仑兹力一定垂直于B 和V 所决定的平面.②四指的指向是正电荷的运动方向或负电荷运动的反方向；（3）特性：洛仑兹力对电荷不做功，它只改变运动电荷的速度方向，不改变速度的大小。

（4）洛伦兹力和安培力的关系：洛伦兹力是安培力的微观表现。

[P2]洛伦兹力计算公式的推导：如图所示，整个导线受到的磁场力（安培力）为F 安=BIL ；其中I=nesv ；设导线中共有N 个自由电子N=nsL ；每个电子受的磁场力为F ，则F 安=NF 。

由以上四式得F=qvB 。

条件是v 与B 垂直。

当v 与B 成θ角时，F=qvB sin θ。

[P3]带电粒子在磁场中的圆周运动：若带电粒子速度方向与磁场方向平行(相同或相反)，带电粒子以不变的速度做匀速直线运动．当带电粒子速度方向与磁场垂直时，带电粒子在垂直于磁感应线的平面内做匀速圆周运动．带电粒子在匀强磁场中仅受洛伦兹力而做匀速圆周运动时，洛仑兹力充当向心力：rmv qvB 2=， 由此可以推导出该圆周运动的半径公式和周期公式：Bqm T ,Bq mv r π2== m )qBR (mv E k 22122==动能[P4]2007年上海卷）在磁感应强度B 的匀强磁场中，垂直于磁场放入一段通电导线。

若任意时刻该导线中有N 个以速度v 做定向移动的电荷，每个电荷的电量为q 。

则每个电荷所受的洛伦兹力f ＝ q v B __，该段导线所受的安培力为F ＝ N q v B ___。

[P5]2007高考理综北京卷）图1是电子射线管示意图.接通电源后，电子射线由阴极沿x 轴方向射出,在荧光屏上会看到一条亮线.要使荧光屏上的亮线向下（z 轴负方向）偏转，在下列措施中可采用的是____B______。

洛伦兹力的研究与实验探究洛伦兹力是电荷在磁场中运动时所受的力，是电磁感应现象的基础之一。

通过对洛伦兹力的研究与实验探究，我们可以深入理解其产生机制，揭示电磁场与电荷之间的相互作用规律，为电磁学的发展做出重要贡献。

一、洛伦兹力的定义和基本原理洛伦兹力是指当带电粒子在磁场中运动时受到的力，它的方向垂直于粒子的运动方向和磁场的方向，并且大小与粒子的电荷量、速度以及磁场的强度有关。

洛伦兹力的表达式为：F = q(v × B)其中，F表示洛伦兹力的大小和方向，q表示粒子的电荷量，v表示粒子的速度向量，B表示磁感应强度向量。

根据右手规则可以确定洛伦兹力的方向。

二、洛伦兹力的研究历程洛伦兹力最早是由荷兰物理学家亨德里克·洛伦兹在19世纪末提出的，他基于麦克斯韦方程组和牛顿第二定律，利用向量分析的方法推导出了洛伦兹力的表达式。

洛伦兹力的研究对于宏观物理学和微观粒子物理学的发展都具有重要意义。

在实验研究方面，科学家们通过一系列的实验来验证洛伦兹力的存在和作用规律。

例如，他们利用导线在磁场中的受力来研究洛伦兹力对电流的影响，通过改变电流方向和磁场强度等条件来观察洛伦兹力的变化。

同时，科学家们也通过将电荷粒子射入磁场中进行轨迹观测，验证了洛伦兹力的垂直性和大小与速度的关系。

三、洛伦兹力的应用洛伦兹力在现实生活和科学研究中有着广泛的应用。

以下列举几个具体的应用领域：1. 电磁感应：洛伦兹力是电磁感应现象的基础，电动机、发电机等设备的工作原理都基于洛伦兹力的作用。

2. 粒子物理学：粒子加速器利用洛伦兹力加速电荷粒子，从而达到研究微观结构和粒子性质的目的。

3. 磁共振成像：洛伦兹力在磁共振成像技术中起到重要作用，利用洛伦兹力的效应可以观察和研究人体内部的结构和器官功能。

4. 磁悬浮交通：洛伦兹力可以实现磁悬浮技术，使列车在轨道上悬浮并高速运行，具有较低的阻力和噪音，提高了交通效率。

四、洛伦兹力的未来发展方向随着科学技术的不断进步，对洛伦兹力的研究也在不断深入。

洛伦兹力计算公式？洛伦兹力的详解？在学习高中物理的时候往往会遇到很多关于物理问题，上课觉着什幺都懂了，可等到做题目时又无从下手。

以至于对于一些意志薄弱、学习方法不对的同学就很难再坚持下来。

过早的对物理没了兴趣，伤害了到高中的学习信心。

收集整理下面的这几个问题，是一些同学们的学习疑问，小编做一个统一的回复，有同样问题的同学，可以仔细看一下。

【问：洛伦兹力计算公式？洛伦兹力的详解?】答：洛伦兹力表达式f=qvb，其中q是带电量，v 是粒子的速度，b是磁感应强度。

需要注意的是，v必须与b垂直，否则需要在b垂直的面内进行投影。

【问：闭合电路欧姆定律的内容是什幺？】答：闭合电路欧姆定律是初中学过的欧姆定律（部分欧姆定律）的补充，恒定电路这章引入了电源电动势与内电阻的概念，总电路中电动势与电流关系：e=i（r+r）=u外+u内，即电池的电动势等于内外总阻值与干路电流之积。

【问：磁场偏转周期的求法？】答：粒子在磁场中做圆周运动的周期t的公式是t=2πm/bq；可在计算题中，这个公式是不能直接使用的，必须推导。

推导要用到向心力公式，带有周期t：qvb=m*v*2π/t，两端同时约去v，即可得周期t的公式，这是最简单的一种推导方法。

【问：高中物理中说的临界态指的是什幺？】答：物体的运动、受力、能量、动量等物理量发生变化（性质上变化）的特殊状态。

比如，原来物体在加速运动，在某时刻其加速度减小为零，此时刻后其加速度开始反向，即开始做减速运动，物体在这一点所对应的状态就是临界态，也叫做临界点。

当然，高中研究的临界态不仅仅拘泥于力学和电磁学，还包括光学的临界角、极限频率等所对应的状态。

【问：课下我要总结哪些内容？】答：及时总结所学内容，对物理学习非常重要。

只有多总结，把问题吃透了，考试中才能够很好的发挥出来。

以上洛伦兹力计。

第五节 运动电荷在磁场中受到的力第一部分1、既然磁场对电流有力的作用，而电流是由电荷的定向移动形成的。

那么磁场是否对运动电荷也有作用力呢? 实验结论：磁场对运动电荷有作用力.2、洛伦兹力：运动电荷在磁场中受到的力叫做洛伦兹力。

专题一 洛伦兹力与安培力的关系安培力是洛伦兹力的宏观表现洛伦兹力是安培力的微观本质(解释)专题二 洛伦兹力大小的推导若有一段长度为L 的通电导线，横截面积为S ，单位体积中含有的自由电荷数为n ，每个自由电荷的电量为q ，定向移动的平均速率为v ，将这段导线垂直于磁场方向放入磁感应强度为B 的匀强磁场中，求每个自由电荷所受的洛伦兹力的大小。

①这段导体所受的安培力F 安=BIL ②电流强度I 的微观表达式I = nqSv③这段导体中含有多少自由电荷数nSL N =(单位体积有n 个自由电荷电荷) 每个自由电荷所受的洛伦兹力3、洛伦兹力大小①F qvB =（电荷运动方向和磁感线方向垂直） ②0F =（电荷运动方向和磁感线方向平行）③sin F qvB θ=（电荷运动方向和磁感线方向夹角为θ）4、洛伦兹力方向 左手定则：如图所示，伸开左手，使拇指和其余四指垂直，并且都与手掌在同一平面内，让磁感线从掌心进入，并使四指指向正电荷运动的方向（负电荷运动的反方向），这时拇指所指的方向就是正电荷（负电荷）在磁场中所受洛伦兹力的方向。

专题三 左力右磁场分析洛伦兹力方向两步走分析洛伦兹力方向①磁感线垂直穿左掌心②四指指正电荷运动方向（负电荷运动的反方向） 拇指指洛伦兹力方向vB vBqvBnLSBnqvSL nLSBIL nLSF F ====安专题四FvB之间夹角①F一定与另外两个东西（vB）垂直洛伦兹力的方向总是既垂直于速度，又垂直于磁场，即F垂直于v和B所组成的平面.F⊥v F⊥B F⊥S v B②但另外两个东西（vB）不一定垂直（可以平行、可以有一般夹角）专题五洛伦兹力的特点洛伦兹力时刻与电荷运动方向垂直，只改变速度的方向，不改变速度的大小，对电荷不做功（力而无功、不计其他力时动能不变）。

公式u=qv的适用条件 在物理学中，有很多重要的公式用于描述物体的运动和相互关系。

其中，公式u=qv是描述电荷在磁场中受力的公式，它涉及到电荷q 、速度v和由磁场引起的力u之间的关系。

本文将详细介绍公式u=qv 的适用条件，解释它的含义，并提供一些实际的例子来加深理解。

一、公式含义： 公式u=qv是根据洛伦兹力的原理推导出来的。

它表示当电荷q以速度v在磁场中运动时，所受到的力u与电荷q和速度v之间有一定的关系。

这个公式揭示了电荷在磁场中的受力情况，为我们理解磁场对电荷的作用提供了重要的参考。

二、适用条件： 1. 电荷与磁场的相互作用：公式u=qv只适用于当电荷与磁场发生相互作用时，即电荷穿过磁场区域的情况。

如果电荷和磁场之间没有相互作用，该公式则不适用。

2. 动量的守恒：公式u=qv的推导过程中基于动量守恒原理。

因此，在应用该公式时，需要保证系统的动量守恒，即在电荷穿过磁场区域的过程中，其他物体的动量保持不变。

3. 电荷速度与磁场方向的关系：该公式适用于电荷速度与磁场方向垂直且速度不变的情况。

当电荷速度与磁场方向平行或呈夹角时，公式的应用可能会复杂化。

4. 忽略其他力的作用：公式u=qv的推导过程中，我们忽略了其他力对电荷运动的影响，仅考虑磁场对电荷的影响。

因此，在应用该公式时，需要排除其他力的干扰，确保磁场对电荷的作用是主导因素。

三、实例说明： 为了更好地理解公式u=qv的适用条件，我们可以通过一些实际的例子来说明： 1. 粒子加速器中的粒子：在粒子加速器中，粒子被加速器加速并穿过磁场区域，其速度与磁场方向垂直且速度恒定。

因此，我们可以使用公式u=qv来描述粒子加速器中粒子所受到的磁场力。

2. 电子在电视显像管中的运动：在电视显像管中，电子被电场加速并穿过磁场区域，最终形成图像。

在这个过程中，电子的速度与磁场方向垂直且速度不变，可以使用公式u=qv来描述电子在磁场中的受力情况。

公式u=qv描述了电荷在磁场中受力的关系。

洛伦兹力公式推导
洛伦兹力公式是一种用来计算物体在某一点处受到的外力的公式，它可以用来求解在一个复杂的机构中，物体受到的外力的大小和方向。

洛伦兹力公式的推导可以分为三步：
第一步，从物理原理出发，推导出洛伦兹力的定义：根据牛顿第二定律，物体受到的外力等于物体的质量乘以加速度，即
F=ma。

而加速度又可以表示为物体在某一点处的加速度，即
a=dv/dt，将其代入F=ma，可得F=m(dv/dt)，即洛伦兹力的定义。

第二步，推导出洛伦兹力公式：将洛伦兹力的定义代入
F=m(dv/dt)，可得F=m(dv/dt)，即洛伦兹力的定义，其中v为
物体在某一点处的速度，而dv/dt则是物体在某一点处的加速度，因此可得F=m(dv/dt)，即洛伦兹力公式。

第三步，将洛伦兹力公式求解：将F=m(dv/dt)代入F=m(dv/dt)，可得F=m(dv/dt)，即洛伦兹力的定义，其中v为物体在某一点
处的速度，而dv/dt则是物体在某一点处的加速度，因此可以
将F=m(dv/dt)求解为F=mv(dv/dx)，即洛伦兹力公式的最终形式。