2.2.2函数的表示法(公开课)

第二课时（2.1函数,2.2函数的表示法）第二课时（2.1函数,2.2函数的表示法）
教学目的：
1. 理解函数的概念，映射的概念；
2. 初步掌握函数的表示法.
教学重点难点：函数，映射的“三要素”，分段表示函
数的解析式.
教学过程：
一、复习：函数的概念，映射的概念，函数的表示法
二、例题
例1 已知函数-5x+2，求f(3), f(-), f(a+1).
例2下列函数中哪个与函数是同一个函数？
⑴
例3 下列各组中的两个函数是否为相同的函数？
①
例5某种笔记本每个5元，买 x{1,2,3,4}个笔记本的钱
数记为y（元），试写出以x为自变量的函数y的解析式，
定义域，值域，并画出这个函数的图像。

例6 国内投寄信函（外埠），每封信函不超过20g付邮
资80分，超过20g而不超过40g付邮资160分，依次类推，每封x g(0x100)的信函应付邮资为（单位：分），
试写出以x为自变量的函数y的解析式，定义域，值域，
并画出这个函数的图像。

三、课堂练习：课本P51练习1，5，6； P56练习 1，2，3
四、作业习题2.1 4，5，6（3）（4）（6）。

则可以对变量进行置换，设法构《2.2.2函数的表示法》导学案问题导学一、 求函数的解析式活动与探究1(1) 已知f(x)是一次函数，且满足3/(x+l) —2/*(x —1) =2x+17,求八x)；(2) 已知/(S+1) =x+2\[x,求/G)；(3) 已知/(尤)+孑*(—x)=工+1,求/G)的解析式.迁移与应用1. 已知八矽是二次函数，且满足/(o)=l, /(x+1) —/(X)=2x,求/G).2. (1)已知£)=2X ,打(x)；(2)已知牙G)—求/G) •求函数解析式的常见方法：(1) 若已知函数类型，可用待定系数法求解.(2) 若不清楚函数类型，比如已知f[g(x)]的解析式，求八x)的解析式，可采用配凑法和 换元法.配凑法是将f[g (x)]右端的代数式配凑成关于g(X)的形式，进而求出f(x)的解析式； 换元法是令gG)=f,然后解出x,即用r 表示x,然后代入ytg(x)]中即可求得的),从而求得产 (X).(3) 构造方程组法：若已知的函数关系较为抽象，程组，通过解方程组求得函数解析式.二、 作函数的图像活动与探究2作出下列函数的图像： (1) y=—x+l, xez ；(2) y=2x 2-4.x~3, 0Wx<3.迁移与应用X %x ,0<XLxNl(2)y= \x~\~ 11+ \x—3 |.2.画出函数)=-『一2*(*>1或*<一1)的图像.一般地，作函数图像主要有三步：列表、描点、连线.作图像时一般应先确定函数的定义域，再化简解析式(有的要表示为分段函数)，再列表、描点画出图像，并在画图像的同时注意一些关键点，如与坐标轴的交点，分段函数的区间端点等.对于常见的一次、二次函数的图像可直接画出来.三、分段函数及其应用活动与探究3已知函麴^)=h，*〉1.(1)求[3, f(—2)的值；(2)画出的图像；⑶求产(x)的定义域和值域.迁移与应用Jx+1,1.已知弥)=]_好3, x〉l,贝妙侦(2)) = ( ).A. 0B. 1C. 2D. 32.画出下列函数的图像，并写出它们的值域：(1)分段函数求值时，一定要注意所给自变量的值所在的范围，根据范围选择相应的解析式代入求得.(2)分段函数的解析式因其特点可以分成两个或两个以上的不同解析式，所以它的图像也由几部分构成，有的可以是光滑的曲线段，有的也可以是一些孤立的点或几段线段.(3)分段函数的定义域与值域的最好求法也是“图像法”，其定义域是自变量x各段取值的并集，值域是各段值域的并集.当堂检测1.已知函数八I)由下表给出：-1 0 1 2f(x) 4 2 0 1则六2)的值为().A. 4B. 2C. 0D. 12./(A-)=|A-2的图像是().4.已知_f(x)满足f(2x—1)=4/,贝仃(x)的解析式为.5.某商场进了10台电脑，每台售价3 000元，试求售出台数x与收款数y之间的函数关系, 分别用列表法、图像法、解析法表示出来.。

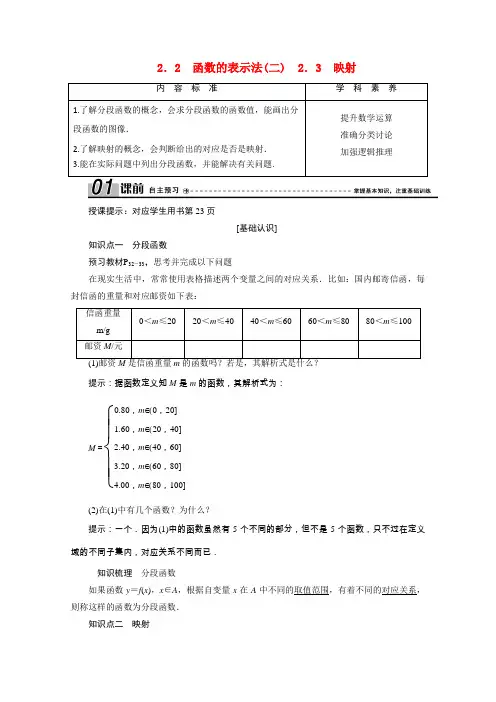
2．2 函数的表示法(二) 2．3 映射内 容 标 准学 科 素 养 1.了解分段函数的概念，会求分段函数的函数值，能画出分段函数的图像．2.了解映射的概念，会判断给出的对应是否是映射．3.能在实际问题中列出分段函数，并能解决有关问题.提升数学运算 准确分类讨论 加强逻辑推理授课提示：对应学生用书第23页[基础认识]知识点一 分段函数预习教材P 32－33，思考并完成以下问题在现实生活中，常常使用表格描述两个变量之间的对应关系．比如：国内邮寄信函，每封信函的重量和对应邮资如下表：信函重量m/g 0＜m ≤2020＜m ≤4040＜m ≤6060＜m ≤8080＜m ≤100邮资M /元提示：据函数定义知M 是m 的函数，其解析式为：M ＝⎩⎪⎨⎪⎧0.80，m ∈(0，20]1.60，m ∈(20，40]2.40，m ∈(40，60]3.20，m ∈(60，80]4.00，m ∈(80，100](2)在(1)中有几个函数？为什么？提示：一个．因为(1)中的函数虽然有5个不同的部分，但不是5个函数，只不过在定义域的不同子集内，对应关系不同而已．知识梳理 分段函数如果函数y ＝f (x )，x ∈A ，根据自变量x 在A 中不同的取值范围，有着不同的对应关系，则称这样的函数为分段函数．知识点二 映射思考并完成以下问题在某次数学测试中，高一(1)班的60名同学都取得了较好的成绩，把该班60名同学的名字构成集合A，他们的成绩构成集合B.(1)A中的每一个元素，在B中有且只有一个元素与之对应吗？提示：是的．(2)从集合A到集合B的对应是函数吗？为什么？提示：不是．因为集合A不是数集．知识梳理设A、B是两个非空的集合，如果按某一个确定的对应关系f，使对于集合A中的任意一个元素x，在集合B中都有唯一确定的元素y与之对应，那么就称对应f：A→B为从集合A到集合B的一个映射．2．映射与函数的关系：映射是从集合A到集合B的一种对应关系，这里的集合A，B可以是数集、点集或其他集合，当A，B是数集时，此时的映射就是函数，即函数是一种特殊的映射．思考：1.“分段函数就是几个函数”，这句话正确吗？提示：不正确．分段函数是一个函数，而非几个函数，只不过是在不同的定义域的子区间上其解析式不同而已．2．已知集合A＝{x|x是中国人}，集合B＝{x|x是每个中国人的身份证号码}，对应关系f：每个中国人对应其自己的身份证号码，那么对应f：A→B是函数吗？是映射吗？提示：不是函数，而是映射．原因是集合A与B是非空的集合，但不是非空的数集．[自我检测]1．已知集合A＝{a，b}，B＝{0,1}，则下列对应不是从A到B的映射是()解析：A、B、D均满足映射定义，C不满足集合A中任一元素在集合B中有唯一元素与之对应，且集合A中元素b在集合B中无唯一元素与之对应．答案：C2．下列图形是函数y ＝－|x |(x ∈[－2,2])的图像的是( )解析：y ＝－|x |＝⎩⎪⎨⎪⎧x ，(－2≤x ＜0)－x ，(0≤x ≤2)，其图像是x 轴下方的两条线段，包括x ＝±2时的两个端点．答案：B3．已知函数f (x )＝⎩⎪⎨⎪⎧x ＋1(x ＞0)，π(x ＝0)，0(x ＜0)，则f (f (－2))＝________.解析：∵f (－2)＝0，∴f (f (－2))＝f (0)＝π. 答案：π授课提示：对应学生用书第23页 探究一 分段函数求值[例1] 已知函数f (x )＝⎩⎪⎨⎪⎧x ＋2，x ＜0，x 2，0≤x ＜2，12x ，x ≥2，(1)求f ⎝⎛⎭⎫f ⎝⎛⎭⎫f ⎝⎛⎭⎫－12的值； (2)若f (x )＝2，求x 的值．[思路点拨] (1)由内到外，先求f ⎝⎛⎭⎫－12，再求f ⎝⎛⎭⎫f ⎝⎛⎭⎫－12，最后求f ⎝⎛⎭⎫f ⎝⎛⎭⎫f ⎝⎛⎭⎫－12； (2)分别令x ＋2＝2，x 2＝2，12x ＝2，分段验证求x .[解析] (1)f ⎝⎛⎭⎫－12＝⎝⎛⎭⎫－12＋2＝32， ∴f ⎝⎛⎭⎫f ⎝⎛⎭⎫－12＝f ⎝⎛⎭⎫32＝⎝⎛⎭⎫322＝94， ∴f ⎝⎛⎭⎫f ⎝⎛⎭⎫f ⎝⎛⎭⎫－12＝f ⎝⎛⎭⎫94＝12×94＝98.(2)当f (x )＝x ＋2＝2时，x ＝0，不符合x ＜0；当f (x )＝x 2＝2时，x ＝±2，其中x ＝2符合0≤x ＜2；当f (x )＝12x ＝2时，x ＝4，符合x ≥2.综上，x 的值是2或4.延伸探究 在题设条件不变的情况下，若f (x )＞3，求x 的取值范围． 解析：当x ＜0时，f (x )＝x ＋2＞3，得x ＞1，显然无解． 当0≤x ＜2时，f (x )＝x 2x ＞3或x ＜－3， ∴3＜xx ≥2时，f (x )＝12x ＞3，得x ＞6.综上，x 的取值范围是(3，2)∪(6，＋∞)． 方法技巧 1.求分段函数函数值的方法：先确定要求值的自变量属于哪一段区间，然后代入该段的解析式求值，直到求出值为止．当出现f (f (x 0))的形式时，应从内到外依次求值．2．已知函数值求字母取值的步骤： (1)先对字母的取值范围分类讨论． (2)然后代入到不同的解析式中． (3)通过解方程求出字母的值．(4)检验所求的值是否在所讨论的区间内． 跟踪探究 f (x )＝⎩⎪⎨⎪⎧x ＋1，x ≤－2，x 2＋2x ，－2＜x ＜2，2x －1，x ≥2.求f (－5)，f (－3)，f ⎝⎛⎭⎫f ⎝⎛⎭⎫－52的值． 解析：由－5∈(－∞，－2]，－3∈(－2,2)，－52∈(－∞，－2]，知f (－5)＝－5＋1＝－4，f (－3)＝(－3)2＋2×(－3)＝3－23， ∵f ⎝⎛⎭⎫－52＝－52＋1＝－32，而－2＜－32＜2， ∴f ⎝⎛⎭⎫f ⎝⎛⎭⎫－52＝f ⎝⎛⎭⎫－32＝⎝⎛⎭⎫－322＋2×⎝⎛⎭⎫－32＝94－3＝－34. 探究二 分段函数的图像[例2] 如图，在边长为4的正方形ABCD 的边上有一点P ，沿着折线BCDA 由点B (起点)向A (终点)运动．设点P 运动的路程为x ，△APB 的面积为y .试求：(1)y 与x 之间的函数关系式； (2)画出y ＝f (x )的图像．[思路点拨] 当点P 在线段BC 上时△APB 的面积随点P 的变化而变化；当点P 在线段CD 上时，△APB 的面积是一个定值；当点P 在线段AD 上时，△APB 的面积随点P 的变化而变化，可见应分三段考虑面积计算．[解析] (1)①当点P 在线段BC 上运动时， S △APB ＝12×4x ＝2x (0≤x ≤4)；②当点P 在线段CD 上运动时， S △APB ＝12×4×4＝8(4＜x ≤8)；③当点P 在线段AD 上运动时，S △APB ＝12×4×(12－x )＝24－2x (8＜x ≤12)．∴y 与x 之间的函数关系式为y ＝⎩⎪⎨⎪⎧2x ，(0≤x ≤4)，8，(4＜x ≤8)，24－2x ，(8＜x ≤12).(2)画出y ＝f (x )的图像，如图所示：方法技巧 1.由于分段函数在定义域的不同区间内解析式不一样，所以它的图像也由几部分构成，有的可以是光滑的曲线段，有的也可以是一些孤立的点或几段线段，画图时要特别注意区间端点处对应点的实虚之分．2．对含有绝对值的函数，要作出其图像，首先根据绝对值的意义去掉绝对值符号，将函数转化为分段函数来画图像．跟踪探究 ，并写出它们的值域： (1)y ＝⎩⎪⎨⎪⎧1x ，0＜x ＜1，2x ，x ≥1；(2)y ＝|x ＋1|＋|x －3|.解析：(1)函数y ＝⎩⎪⎨⎪⎧1x ，0＜x ＜1，2x ，x ≥1的图像如图①，观察图像，得函数的值域为(1，＋∞)．(2)将原函数式中的绝对值符号去掉， 化为分段函数y ＝⎩⎪⎨⎪⎧－2x ＋2，x ≤－1，4，－1＜x ≤3，2x －2，x ＞3，它的图像如图②.观察图像，得函数的值域为[4，＋∞)．探究三 映射[例3] 已知A ＝{a ，b ，c }，B ＝{－1,2}．则从A 到B 可以建立多少个不同的映射？ [解析] 从A 到B 可以建立8个映射，如下图所示．延伸探究 1.(改变问法)本例条件不变，则从B 到A 的映射有多少个？ 解析：从B 到A 可以建立9个映射，如图所示．2．(增加条件)本例若增加条件：f (a )＋f (b )＋f (c )＝A 到B 的映射有多少个？解析：欲使f (a )＋f (b )＋f (c )＝0，需a ，b ，c 中有两个元素对应－1，一个元素对应2，共可建立3个映射．3．(变换条件)本例条件变为设A ＝{a ，b ，c }，B ＝{－1,0,1}，若从A 到B 的映射f 满足：f (a )＋f (b )＝f (c )，求这样的映射f 的个数．解析：要确定映射f ，只需确定A 中的每个元素对应的像即可，即确定f (a )，f (b )，f (c )的值，由题可知f (a )，f (b )，f (c )∈{－1,0,1}，且满足f (a )＋f (b )＝f (c )，列表由上表可知，所求的映射有7个． 方法技巧 判断是否为映射的几大要点：(1)集合A ，B 的元素是任意的，没有任何限制；(2)映射是有方向的，A 到B 的映射与B 到A 的映射往往是不一样的；(3)映射要求对集合A 中的每一个元素在集合B 中都有元素与之对应，而且这个与之对应的元素是唯一的，这样集合A 中元素的任意性和集合B 中与其对应的元素的唯一性就构成了映射的核心；(4)映射允许集合B 中存在元素在A 中没有元素与其对应；(5)映射是特殊的对应，即“多对一”或“一对一”的对应，而对应不一定是映射，其中“一对多”的对应不是映射．跟踪探究 ，哪些是从集合A 到集合B 的映射？ (1)A ＝B ＝N ＋，对应关系f ：x →y ＝|x －3|；(2)A ＝R ，B ＝{0,1}，对应关系f ：x →y ＝⎩⎪⎨⎪⎧1，x ≥00，x ＜0；(3)设A ＝{矩形}，B ＝{实数}，对应关系f ：矩形的面积．解析：(1)集合A 中的3，在f 作用下得0，但0∉B ，即3在集合B 中没有相对应的元素，所以不是映射．(2)对于集合A 中任意一个非负数都唯一对应元素1，对于集合A 中任意一个负数都唯一对应元素0，所以是映射．(3)对于每一个矩形，它的面积是唯一确定的，所以f 是从集合A 到集合B 的映射.授课提示：对应学生用书第25页[课后小结]1．对分段函数的理解(1)分段函数是一个函数而非几个函数；分段函数的定义域是各段上“定义域”的并集，其值域是各段上“值域”的并集．(2)分段函数的图像应分段来作，特别注意各段的自变量取值区间端点处函数的取值情况，以决定这些点的虚实情况．2．函数与映射的关系映射f ：A →B ，其中A ，B 是两个非空集合；而函数y ＝f (x )，x ∈A ，A 为非空实数集，其值域也是数集，于是函数是数集到数集的映射．由此可知，映射是函数的推广，函数是一种特殊的映射．[素养培优]分段函数容易在分类讨论中出错 易错案例：某质点30 s 内运动速度v 是时间t 的函数，它的图像如图．用解析式法表示出这个函数，并求出9 s 时质点的速度．易错分析：解决这类问题的关键是根据自变量的取值情况决定其对应的运算关系，即保持自变量的取值范围与对应关系的一致性，一般需分类讨论求解、考查逻辑推理、分类讨论的学科素养．自我纠正：整体看表达式不能用一个式子写出，但可以分段求得．v (t )＝⎩⎪⎨⎪⎧10＋t ，t ∈[0，5)，3t ，t ∈[5，10)，30，t ∈[10，20)，－3t ＋90，t ∈[20，30).当t＝9时，v(9)＝3×9＝27 cm/s.。

2.2 函数的表示法
教学目标
1．掌握函数的三种表示法，即解析法、列表法和图象法；
2．会根据实际问题中的条件列出函数解析式；
3．通过本节的教学，进一步向学生渗透事物间是普遍联系和相互转化的辨证唯物主义观点；4．通过本节的教学，培养学生把实际问题抽象成数学问题的能力，即数学地发现问题、提出问题和解决问题的能力.
教学重点和难点
重点：函数的三种表示方法.
难点：函数三种表示法的应用.
让两个学生到黑板上板书.学生思考、倾听、理解。