下载文档原格式
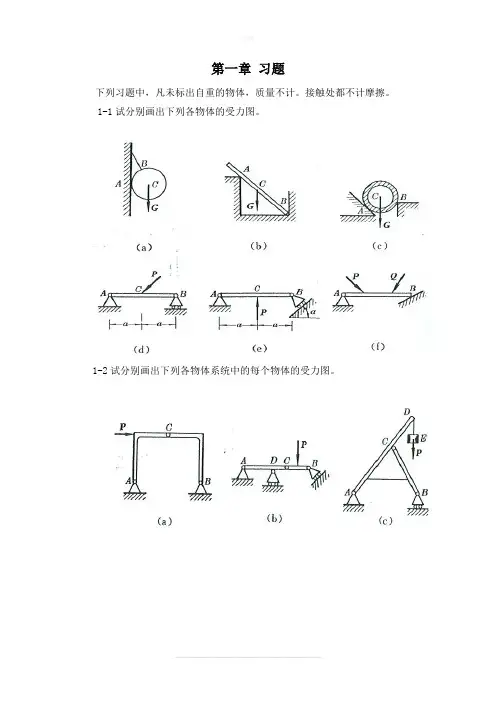
第一章习题下列习题中，凡未标出自重的物体，质量不计。
接触处都不计摩擦。
1-1试分别画出下列各物体的受力图。
1-2试分别画出下列各物体系统中的每个物体的受力图。
1-3试分别画出整个系统以及杆BD，AD，AB（带滑轮C，重物E和一段绳索）的受力图。
1-4构架如图所示，试分别画出杆HED，杆BDC及杆AEC的受力图。
1-5构架如图所示，试分别画出杆BDH，杆AB，销钉A及整个系统的受力图。
1-6构架如图所示，试分别画出杆AEB，销钉A及整个系统的受力图。
1-7构架如图所示，试分别画出杆AEB，销钉C，销钉A及整个系统的受力图。
1-8结构如图所示，力P作用在销钉C上，试分别画出AC，BCE及DEH部分的受力图。
参考答案1-1解：1-2解：1-3解：1-4解：1-5解：1-6解：1-7解：1-8解：第二章 习题参考答案2-1解：由解析法，23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故： 22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN ==++=∑13sin 45sin 450RY F Y P P ==-=∑故： 223R RX RY F F F KN=+=方向沿OB 。
2-3解：所有杆件均为二力杆件，受力沿直杆轴线。
（a ） 由平衡方程有：0X =∑sin 300ACAB FF -=0Y =∑cos300ACFW -=联立上二式，解得：0.577AB F W =（拉力）1.155AC F W=（压力）（b ） 由平衡方程有：0X =∑cos 700ACAB F F -=0Y =∑sin 700ABFW -=联立上二式，解得：1.064AB F W =（拉力）0.364AC F W=（压力）（c ） 由平衡方程有：0X =∑cos 60cos300ACAB FF -=0Y =∑sin 30sin 600ABAC FF W +-=联立上二式，解得：0.5AB F W=(拉力)0.866AC F W=（压力）（d ） 由平衡方程有：0X =∑sin 30sin 300ABAC F F -=0Y =∑cos30cos300ABAC FF W +-=联立上二式，解得：0.577AB F W =(拉力)0.577AC F W=(拉力)2-4解：（a）受力分析如图所示：由x=∑22cos45042RAF P=+15.8RAF KN∴=由Y=∑22sin45042RA RBF F P+-=+7.1RBF KN∴=(b)解：受力分析如图所示：由0x =∑cos45cos 45010RA RB F F P ⋅--= 0Y =∑sin 45sin 45010RA RB F F P ⋅+-=联立上二式，得：22.410RA RB F KN F KN==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以： 5RA F KN=（压力）5RB F KN=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解：受力分析如图所示，取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后，解得：0.707RA F P=0.707RB F P=由二力平衡定理 0.707RB CB CBF F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600ABAC FF W +-=联立上二式，解得：7.32AB F KN =-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程由0Y =∑ sin cos 0BDT T αα'-=230BDT T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑ sin 0BC F P α-=sin BC PF α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '=故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：0x =∑sin 75sin 750ABAD FF -=0Y =∑cos 75cos 750ABAD FF P +-=联立后可得：2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：0x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD PF F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x=∑cos cos300RA DCF F Pα+-=Y=∑sin sin300RAF Pα-=联立上二式得：2.92RAF KN=1.33DCF KN=（压力）列C点平衡x=∑405DC ACF F-⋅=Y=∑305BC ACF F+⋅=联立上二式得：1.67ACF KN=（拉力）1.0BCF KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡0x =∑05RD REF F '-= 0Y =∑05RD F Q -=联立方程后解得： 5RD F Q =2REF Q '=（2）取ABCE 部分，对C 点列平衡0x =∑cos 450RERA FF -=0Y =∑sin 450RBRA FF P --=且RE REF F '=联立上面各式得：22 RAFQ=2RBF Q P=+（3）取BCE部分。
工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。
（a）（b）（c）2 第一章静力学基础（d）（e）（f）（g）第一章静力学基础 3 1-2 试画出图示各题中AC杆（带销钉）和BC杆的受力图（a）（b）（c）（a）4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计，各物自重除图中已画出的外均不计。
（a）第一章静力学基础 5 （b）（c）（d）6 第一章静力学基础（e）第一章静力学基础7 （f）（g）8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央，如图所示。
梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上，如第二章 平面力系 9图所示。
转动绞车，物体便能升起。
设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线，下垂距离CD =f =1m ，两电线杆间距离AB =40m 。
电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。
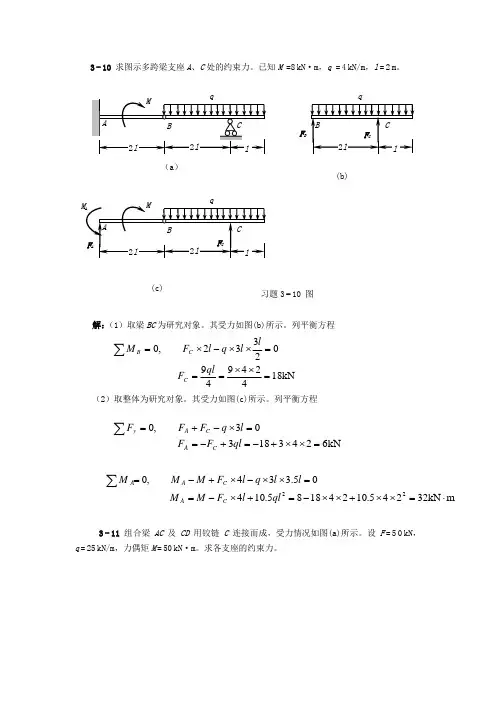
3-10 求图示多跨梁支座A 、C 处的约束力。
已知M =8kN ·m ，q =4kN/m ，l =2m 。
解：（1）取梁BC 为研究对象。
其受力如图(b)所示。
列平衡方程 （2）取整体为研究对象。
其受力如图(c)所示。
列平衡方程3-11 组合梁 AC 及CD 用铰链C 连接而成，受力情况如图(a)所示。
设F =50kN ，q =25kN/m ，力偶矩M =50kN ·m 。
求各支座的约束力。
F BkN1842494902332,0=⨯⨯===⨯⨯-⨯=∑ql F ll q l F M C C B kN624318303,0=⨯⨯+-=+-==⨯-+=∑ql F F l q F F F C A C A ymkN 32245.10241885.10405.334,022⋅=⨯⨯+⨯⨯-=+⨯-==⨯⨯-⨯+-=∑ql l F M M l l q l F M M MC A C A A解：（1）取梁CD 为研究对象。
其受力如图(c)所示。
列平衡方程（2）取梁AC 为研究对象。
其受力如图(b)所示，其中F ′C =F C =25kN 。
列平衡方程F C(b)(c)´CkN 25450252420124,0=+⨯=+==-⨯⨯-⨯=∑M q F M q F MD D CkN 25450256460324,0=-⨯=-==-⨯⨯+⨯-=∑M q F M q F MC C D)kN(25225225250222021212,0↓-=⨯-⨯-='--==⨯'-⨯⨯-⨯+⨯-=∑CA C A BF q F F F q F F MkN150225425650246043212,0=⨯+⨯+='++==⨯'-⨯⨯-⨯-⨯=∑CB CB AF q F F F q F F M6−1作图示杆件的轴力图。
解：在求AB 段内任一截面上的轴力时，在任一截面1−1处截断，取左段为脱离体（图c ），并设轴力F N1为拉力。
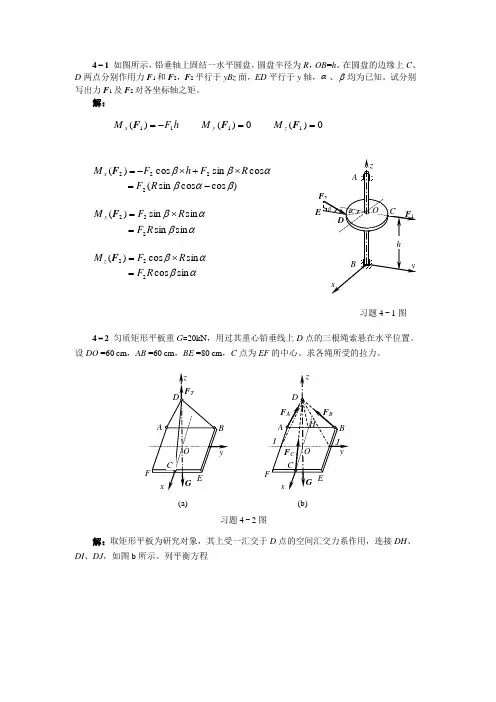
4-1 如图所示，铅垂轴上固结一水平圆盘，圆盘半径为R ，OB =h 。
在圆盘的边缘上C 、D 两点分别作用力F 1和F 2，F 2平行于yBz 面，ED 平行于y 轴，α、β均为已知。
试分别写出力F 1及F 2对各坐标轴之矩。
解：)cos cos sin (cos sin cos )(2222βαβαββ-=⨯+⨯-=R F R F h F M x Fαβαβsin sin sin sin )(222R F R F M y =⨯=Fαβαβsin cos sin cos )(222R F R F M z =⨯=F4-2 匀质矩形平板重G =20kN ，用过其重心铅垂线上D 点的三根绳索悬在水平位置。
设DO =60cm ，AB =60cm ，BE =80cm ，C 点为EF 的中心。
求各绳所受的拉力。
解：取矩形平板为研究对象，其上受一汇交于D 点的空间汇交力系作用，连接DH 、DI 、DJ ，如图b 所示。
列平衡方程)(0)()(1111==-=F F F z y x M M h F M(a)(b)由（1）（2）（3）式联立解得4-3图示空间构架由三根无重直杆组成，在D 端用球铰链连接，A 、B 和C 端则用球铰链固定在水平地面上。
如果挂在D 端的物重P =10kN ，试求铰链A 、B 和C 的约束力。
解：取空间构架及物体为研究对象，受力如图（b ）所示。
建立坐标系如图，列平衡方程由（1）、（2）、（3）式联立解得kN02.12kN 51.6===C B A F F F ()()()302052106061106061106000205210406110406110400,01,,0,0=-++=-++==-+=-+==∴===-=∑∑∑C B A C B A zC B A C B AxBA B A yF F FG DC DO F DB DO F DA DO F FF F F DO COF BD BJ F AD AI F FF F BD AD BH AH BD BHF AD AH F F Θ(a)(b)0cos 45cos 450(1)0sin 45cos30sin 45cos30cos150(2)0sin 45sin 30sin 45sin 30sin150(3)x A B yA B C zA B C FF F F F F F FF F FG =-︒+︒==-︒⨯︒-︒⨯︒-︒==-︒⨯︒-︒⨯︒-︒-=∑∑∑26.39kN 33.46kNA B C F F F ==-=4-4 挂物架如图所示，不计重量的三杆用球铰链连接于O ，平面BOC 是水平面，且OB =OC ，角度如图。
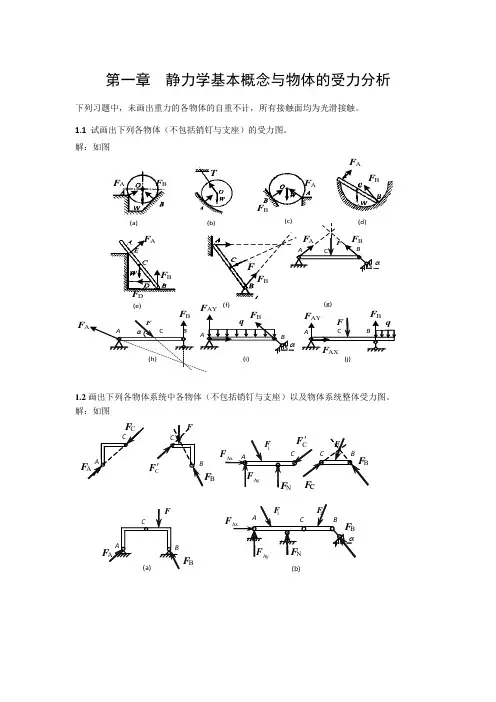
第一章 静力学基本概念与物体的受力分析下列习题中，未画出重力的各物体的自重不计，所有接触面均为光滑接触。
1.1 试画出下列各物体（不包括销钉与支座）的受力图。
解：如图(g)(j)P (a)(e)(f)WWF F A BF DF BF AF ATF BA1.2画出下列各物体系统中各物体（不包括销钉与支座）以及物体系统整体受力图。
解：如图F BB(b)(c)C(d)CF D(e)AFD(f)FD(g)(h)EOBO E F O(i)(j) BYFB XBFXE(k)1.3铰链支架由两根杆AB、CD和滑轮、绳索等组成，如题1.3图所示。
在定滑轮上吊有重为W的物体H。
试分别画出定滑轮、杆CD、杆AB和整个支架的受力图。
解：如图'FD1.4题1.4图示齿轮传动系统，O1为主动轮，旋转方向如图所示。
试分别画出两齿轮的受力图。
解：1o xF2o xF2o yF o yFFF'1.5结构如题1.5图所示，试画出各个部分的受力图。
解：第二章汇交力系2.1 在刚体的A 点作用有四个平面汇交力。
其中F 1＝2kN ，F 2=3kN ，F 3=lkN ， F 4=2.5kN ，方向如题2.1图所示。
用解析法求该力系的合成结果。
解 0001423c o s 30c o s 45c o s 60c o s 45 1.29Rx F X F F F F KN ==+--=∑00001423sin30cos45sin60cos45 2.54Ry F Y F F F F KN ==-+-=∑2.85R F KN ==0(,)tan63.07Ry R RxF F X arc F ∠==2.2 题2.2图所示固定环受三条绳的作用，已知F 1＝1kN ，F 2=2kN ，F 3=l.5kN 。
求该力系的合成结果。
解：2.2图示可简化为如右图所示023cos60 2.75Rx F X F F KN ==+=∑ 013sin600.3Ry F Y F F KN ==-=-∑2.77R F KN ==0(,)tan6.2Ry R RxF F X arc F ∠==-2.3 力系如题2.3图所示。
第一章 习题下列习题中，凡未标出自重的物体，质量不计。
接触处都不计摩擦。
1-1试分别画出下列各物体的受力图。
1-2试分别画出下列各物体系统中的每个物体的受力图。
1-3试分别画出整个系统以及杆BD ，AD ，AB （带滑轮C ，重物E 和一段绳索）的受力图。
1-4构架如图所示，试分别画出杆HED ，杆BDC 及杆AEC 的受力图。
1-5构架如图所示，试分别画出杆BDH ，杆AB ，销钉A 及整个系统的受力图。
1-6构架如图所示，试分别画出杆AEB ，销钉A 及整个系统的受力图。
1-7构架如图所示，试分别画出杆AEB ，销钉C ，销钉A 及整个系统的受力图。
1-8结构如图所示，力P 作用在销钉C 上，试分别画出AC ，BCE 及DEH 部分的受力图。
参考答案1-1解：1-2解： 1-3解： 1-4解： 1-5解： 1-6解： 1-7解： 1-8解：第二章 习题参考答案2-1解：由解析法，23cos 80RX F X P P Nθ==+=∑故：161.2R F N==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有故：3R F KN==方向沿OB 。
2-3解：所有杆件均为二力杆件，受力沿直杆轴线。
（a ） 由平衡方程有：联立上二式，解得：0.577AB F W =（拉力） 1.155AC F W =（压力） （b ） 由平衡方程有：联立上二式，解得：1.064AB F W =（拉力） 0.364AC F W =（压力） （c ） 由平衡方程有：联立上二式，解得：0.5AB F W =(拉力) 0.866AC F W =（压力）（d ） 由平衡方程有：联立上二式，解得：0.577AB F W =(拉力) 0.577AC F W =(拉力)2-4解：（a ）受力分析如图所示：由0x =∑ cos 450RA F P =由Y =∑sin 450RA RB F F P +-=(b)解：受力分析如图所示：由 联立上二式，得：2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以： 5RA F KN =（压力）5RB F KN =（与X 轴正向夹150度） 2-6解：受力如图所示：已知，1R F G = ，2AC F G =由x =∑ cos 0AC r F F α-=由0Y =∑ sin 0AC N F F W α+-=2-7解：受力分析如图所示，取左半部分为研究对象由cos45cos450RA CB P F F --=联立后，解得： 0.707RA F P =由二力平衡定理 0.707RB CB CB F F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑ cos60cos300AC AB F F W ⋅--=联立上二式，解得： 7.32AB F KN =-（受压）27.3AC F KN =（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑ sin cos 0DB T W αα-=（2）取B 点列平衡方程由0Y =∑ sin cos 0BD T T αα'-=2-10解：取B 为研究对象：由0Y =∑ sin 0BC F P α-=取C 为研究对象：由cos sin sin 0BC DC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BC BC F F '= 解得： 取E 为研究对象：由0Y =∑ cos 0NH CE F F α'-=CECE F F '=故有：2-11解：取A 点平衡：联立后可得：2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：由对称性及 AD AD F F '=2-12解：整体受力交于O 点，列O 点平衡由0x =∑cos cos300RADC FF P α+-=联立上二式得： 2.92RA F KN =1.33DC F KN =（压力） 列C 点平衡联立上二式得： 1.67AC F KN =（拉力）1.0BC F KN =-（压力） 2-13解：（1）取DEH 部分，对H 点列平衡联立方程后解得： RD F （2）取ABCE 部分，对C 点列平衡且 RE RE F F '=联立上面各式得： RA F =（3）取BCE 部分。
第4章影响线1.【解】 （1）图4-22（2）图4-231M 的影响线A F 的影响线SA M 的影响线C F 的影响线SC（3）图4-24（4）图4-25（1）图4-26M CF SC（2）图4-273. 【解】（1）图4-28判别60kN 和20kN 是否为临界荷载403<60+20+309 40+603>20+309所以60kN 是临界荷载40+603>20+309 40+60+203>309所以20kN 不是临界荷载C 0.752.251.751.25M CC0.250.750.5830.417F SCC0.0830.750.523F SC0.250.25M Cmax =40×0.75+60×2.25+20×1.75+30×1.25=237.5kN ·mF SCmax =40×0.75+60×0.583+20×0.417+30×0.25 =80.82kN ·mF SCmin =−60×0.083−20×0.25+30×0.583 =−9.16kN ·m判别478.5kN 是否为临界荷载03<478.5+324.5+324.59 478.53>324.5×29所以478.5kN 是临界荷载判别左边324.5kN 是否为临界荷载478.53>324.5×29 478.5+324.53>324.59所以324.5kN 不是临界荷载C2.251.88750.6875C0.750.250.25M CF SCF SCC0.750.6290.2294. 【解】 （1）图4-30①求使跨中截面C 发生最大弯矩的临界荷载 判别左边324.5kN06<324.5+324.56 324.56≥324.56所以第一个324.5kN 是临界荷载1.2m4.8m0.636m②求临界载荷的位置因为对称，右边集中力也为临界荷载，产生相同大小的跨中弯矩合力F =629kN ，所以 x =l 2−a 2=122−2.42=4.8m③求绝对最大弯矩M Cmax =478.5×2.25+324.5×1.8875+324.5×0.6875 =1912.21kN ·mF SCmax =478.5×0.75+324.5×0.629+324.5×0.229 =637.296kN ·mF SCmin =−324.5×0.25 =−81.125kN ·mM Cmax =324.5×3+324.5×0.6 =1168.2kN ·m（2）图4-31①求使跨中截面C 发生最大弯矩的临界荷载06≤120+606 1206≥60+206所以120kN 是临界荷载2m4m136m②求临界载荷的位置因为对称，右边集中力也为临界荷载，产生相同大小的跨中弯矩合力F =200kN ，因为 200∙x ′=60×4+20×8 所以 x ′=2m =a x =l2−a2=122−22=5m ，此时20kN 不在范围内重新计算合力F =120+60=180kN ，因为 180∙x ′=60×4 所以 x ′=1.333m =ax =l 2−a 2=122−1.3332=5.334m ③求绝对最大弯矩5. 【解】①自重下的弯矩图kN·mM Cmax =120×3+60×1=420kN ·m②各截面弯矩影响线及相应不利荷载的位置M 1的影响线M 2的影响线M 3的影响线单位：kN·m移动荷载下弯矩包络图③叠加①和②的弯矩图450706.7706.7450单位：kN·m0.5m0.5m。
第一章习题下列习题中，凡未标出自重的物体，质量不计。
接触处都不计摩擦。
1-1试分别画出下列各物体的受力图。
1-2试分别画出下列各物体系统中的每个物体的受力图。
1-3试分别画出整个系统以及杆BD，AD，AB（带滑轮C，重物E和一段绳索）的受力图。
1-4构架如图所示，试分别画出杆HED，杆BDC及杆AEC的受力图。
1-5构架如图所示，试分别画出杆BDH，杆AB，销钉A及整个系统的受力图。
1-6构架如图所示，试分别画出杆AEB，销钉A及整个系统的受力图。
1-7构架如图所示，试分别画出杆AEB，销钉C，销钉A及整个系统的受力图。
1-8结构如图所示，力P作用在销钉C上，试分别画出AC，BCE及DEH部分的受力图。
参考答案1-1解：1-2解：1-3解：1-4解：1-5解：1-6解：1-7解：1-8解：第二章 习题参考答案2-1解：由解析法，23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故： 22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN ==++=∑13sin 45sin 450RY F Y P P ==-=∑故： 223R RX RY F F F KN=+=方向沿OB 。
2-3解：所有杆件均为二力杆件，受力沿直杆轴线。
（a ）由平衡方程有：0X =∑sin 300ACAB FF -=0Y =∑cos300ACFW -=联立上二式，解得：0.577AB F W =（拉力）1.155AC F W=（压力）（b ）由平衡方程有：0X =∑cos 700ACAB FF -=0Y =∑sin 700ABFW -=联立上二式，解得：1.064AB F W =（拉力）0.364AC F W=（压力）（c ）由平衡方程有：0X =∑cos 60cos300ACAB FF -=0Y =∑sin 30sin 600ABAC FF W +-=联立上二式，解得：0.5AB F W=(拉力) 0.866AC F W=（压力）（d ）由平衡方程有：0X =∑sin 30sin 300ABAC FF -=0Y =∑cos30cos300ABAC FF W +-=联立上二式，解得：0.577AB F W =(拉力) 0.577AC F W=(拉力)2-4解：（a）受力分析如图所示：由x=∑22cos45042RAF P-=+15.8RAF KN∴=由Y=∑22sin45042RA RBF F P+-=+7.1RBF KN∴=(b)解：受力分析如图所示：由0x =∑cos 45cos 45010RA RB F F P ⋅--= 0Y =∑sin 45sin 45010RA RB F F P ⋅+-=联立上二式，得：22.410RA RB F KN F KN==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以： 5RA F KN=（压力）5RB F KN=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解：受力分析如图所示，取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后，解得：0.707RA F P=0.707RB F P=由二力平衡定理 0.707RB CB CBF F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600ABAC FF W +-=联立上二式，解得：7.32AB F KN =-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程由0Y =∑ sin cos 0BDT T αα'-=230BDT T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑ sin 0BC F P α-=sin BC PF α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '=故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：0x =∑sin 75sin 750ABAD FF -=0Y =∑cos 75cos 750ABAD FF P +-=联立后可得：2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：0x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD PF F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x=∑cos cos300RA DCF F Pα+-=Y=∑sin sin300RAF Pα-=联立上二式得：2.92RAF KN=1.33DCF KN=（压力）列C点平衡x=∑405DC ACF F-⋅=Y=∑305BC ACF F+⋅=联立上二式得：1.67ACF KN=（拉力）1.0BCF KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡0x =∑05RD REF F '-= 0Y =∑05RD F Q -=联立方程后解得： 5RD F Q =2REF Q '=（2）取ABCE 部分，对C 点列平衡0x =∑cos 450RERA FF -= 0Y =∑sin 450RBRA FF P --=且RE REF F '=联立上面各式得：22RA F Q =2RB F Q P=+（3）取BCE 部分。
4-1 如图所示，铅垂轴上固结一水平圆盘，圆盘半径为R ，OB =h 。
在圆盘的边缘上C 、D 两点分别作用力F 1和F 2，F 2平行于yBz 面，ED 平行于y 轴，α、β均为已知。
试分别写出力F 1及F 2对各坐标轴之矩。
解：)cos cos sin (cos sin cos )(2222βαβαββ-=⨯+⨯-=R F R F h F M x Fαβαβsin sin sin sin )(222R F R F M y =⨯=Fαβαβsin cos sin cos )(222R F R F M z =⨯=F4-2 匀质矩形平板重G =20kN ，用过其重心铅垂线上D 点的三根绳索悬在水平位置。
设DO =60cm ，AB =60cm ，BE =80cm ，C 点为EF 的中心。
求各绳所受的拉力。
解：取矩形平板为研究对象，其上受一汇交于D 点的空间汇交力系作用，连接DH 、DI 、DJ ，如图b 所示。
列平衡方程)(0)()(1111==-=F F F z y x M M h F M(a)(b)由（1）（2）（3）式联立解得4-3图示空间构架由三根无重直杆组成，在D 端用球铰链连接，A 、B 和C 端则用球铰链固定在水平地面上。
如果挂在D 端的物重P =10kN ，试求铰链A 、B 和C 的约束力。
解：取空间构架及物体为研究对象，受力如图（b ）所示。
建立坐标系如图，列平衡方程由（1）、（2）、（3）式联立解得kN02.12kN 51.6===C B A F F F ()()()302052106061106061106000205210406110406110400,01,,0,0=-++=-++==-+=-+==∴===-=∑∑∑C B A C B A zC B A C B Ax BA B A y F F F G DC DO F DB DO F DA DO F FF F F DO COF BD BJ F AD AI F F F F BD AD BH AH BD BHF AD AH F F (a)(b)0cos 45cos 450(1)0sin 45cos30sin 45cos30cos150(2)0sin 45sin 30sin 45sin 30sin150(3)x A B yA B C zA B C FF F F F F F FF F FG =-︒+︒==-︒⨯︒-︒⨯︒-︒==-︒⨯︒-︒⨯︒-︒-=∑∑∑26.39kN 33.46kNA B C F F F ==-=4-4 挂物架如图所示，不计重量的三杆用球铰链连接于O ，平面BOC 是水平面，且OB =OC ，角度如图。
若在 O 点挂一重物G ，重为1000N ，求三杆所受的力。
解：取挂物架及物体为研究对象，受力如图（b ）所示。
建立坐标系如图，列平衡方程4-5 一力F 沿正立方体的对角线BK 作用，方向如图示。
设F =200N ，正立方体边长为2m ，求力F 对O 点之矩矢的大小及方向。
解：力F 在三个坐标轴上的投影为，力F 对三个坐标轴的矩为G(a)(b)0cos 45010001414N 0sin 45cos 450707Nsin 45cos 450707NzA A xB A B yCA C F F FF F F F FFF F F =-︒-====-=--︒⨯︒===+︒⨯︒==∑∑∑cos 45sin 45x y z F FF F FF F F =︒==-︒==-=4-6 轴AB 与铅直线成α角，悬臂CD 垂直地固定在轴上，其长为a ，并与铅直面zAB 成θ角，如图所示。
如在点D 作用铅直向下的力P ，求此力对轴AB 的矩。
解：力P 对轴AB 的矩为θαθαsin sin sin sin Pa aP M AB =⨯⨯=()2()2()0()20()200=230.95N m()0()2200230.95N mx z y y x z z y x M yF zF F F M zF xF F F FM xF yF F F=-=⨯-⨯==-=-⨯===⋅=-=⨯-===-⋅F FF()326.60N mo M ===⋅F cos(,)0,230.95cos(,)0.707,326.60230.95cos(,)0.707326.60x o oy o oz o o MM M M M M =====-===-M i M j M k4-7 图示三圆盘A 、B 和C 的半径分别为150mm 、100mm 和50mm 。
三轴OA 、OB 和OC 在同一平面内，AOB ∠为直角，在这三圆盘上分别作用力偶，组成各力偶的力作用在轮缘上，它们的大小分别等于10N 、20N 和F 。
如这三圆盘所构成的物系处于平衡，不计物系重量，求能使此物系平衡的力F 的大小和角α。
解：此力系为空间力偶系，列平衡方程由（1）、（2）式联立解得4-8 截面为工字形的立柱受力如图示，试求此力向截面形心C 平移的结果。
解：将力F 向截面形心C 平移的结果为一个力F'和一个力偶M C4-9 力系中F 1=100N ，F 2=300N ，F 3=200N 。
各力作用线的位置如图所示，试将力系向原点O 简化。
101502502cos(90)0(1)201002502sin(90)0(2)xyMF M F αα=-⨯⨯+⨯⨯-︒==-⨯⨯+⨯⨯-︒=∑∑143.1350NF α=︒=()0.125(100)0012.5kN m ()00(0.05)(100)5kN m ()(0.05)00.12500()()()12.55kN mx z y y x z z y x c x y z M yF zF M zF xF M xF yF M M M =-=⨯--⨯=-⋅=-=⨯--⨯-=-⋅=-=-⨯-⨯==++=--⋅F F F M F F F i j 0,0100kN100kNx y z F F F ===-'=-F k解：将力系向原点O 简化得4-10 在图示起重机中，AB = BC = AD = AE ；点A 、B 、D 和E 等均为球铰链连接，如三角形ABC 的投影为AF 线，AF 与y 轴夹角为α，如图。
求铅垂支柱和各斜杆的内力。
N59.10512001005100100N61.24913330013100300N29.3545220013230051002001310020031232=-=-=='=⨯==='-=-⨯-=--=='∑∑∑F F F F F F F F F F F z Rzy Ryx RxmN 59.1033.0522002.01333003.051002002.013100300)(mN 64.361.01323002.01001.0131002002.0)(mN 78.513.0512001.01333003.051001001.013100300)(322132⋅=⨯+⨯⨯=⨯+⨯==⋅=⨯-⨯-=⨯-⨯-==⋅-=⨯-⨯⨯-=⨯-⨯-==∑∑∑F F M M F F M M F F M M z z y y x x F F F解：取C 铰及重物为研究对象，受力如图（b ）所示。
建立坐标系如图，列平衡方程 取B 铰为研究对象，受力如图（c ）所示。
且F'CB =F CB ，列平衡方程cos 450cos 450sin 45cos cos 0sin 45()2zCA CA xCA CB CB CA F F F FF FF F F F F αα=-︒-==-=︒=-︒-==-︒=-=∑∑0sin 45sin 45sin 45sin 45sin 0(1)0sin 45cos 45sin 45cos 45cos 0(2)(3)xBD BE CByBD BE CBCB CB F F F F FF F F F F F αα='︒⨯︒-︒⨯︒+=='-︒⨯︒-︒⨯︒+='==∑∑(a) (b) (c)由（1）、（2）式联立解得4-11 水平轴上装有两个带轮C 和D ，轮的半径r 1=20cm ，r 2=25cm ，轮C 的胶带是水平的，其拉力F 2 = 2F 1=5000N ，轮D 的胶带与铅垂线成角 30=α，其拉力F 3 = 2F 4；不计轮轴的重量。
求在平衡情况下拉力F 3 和F 4的大小及轴承约束力。
解：取水平轴及两个带轮为研究对象，受力如图（b ）所示。
列平衡方程N40002N200025.02.025000220,0)(4321142424111124231211===⨯===-+-=-+-=∑F F r r F F r F r F r F r F r F r F r F r F MyF N412525.0250035.130sin 2000305.035.130sin 3205.0)()15.0(sin )()5.015.0(0)(142143-=⨯⨯-⨯︒⨯⨯-==⨯-⨯︒-⨯-=+-+⨯+-++-=∑Bx Bx Bx zF F F F F F F F F MαFN389725.130cos 2000305.130cos 320)15.0(cos )()5.015.0(0)(443=⨯︒⨯⨯==⨯︒-⨯=+⨯+-++=∑Bz Bz Bz xF F F F F F MαF(cos sin )(cos sin )BD BE F F F F αααα=-=+0cos 45cos 45cos 0zBD BE BA BA FF F F F αα=-︒-︒-==∑ 习题4(a)N129930cos 20003389730cos 3030cos 30cos )(04443=︒⨯⨯+-=︒+-==︒-+=+-+=∑F F F F F F F F F F FBz Az Bz Az Bz Az zαN637530sin 2000325003)4125(30sin 33030sin 330sin )(041414321-=︒⨯⨯-⨯---=︒---==︒+++=+++++=∑F F F F F F F F F F F F F F FBx Ax Bx Ax Bx Ax xα4-12 水平轴上装有两个凸轮，一个凸轮上作用已知力F 1=800N ，另一个凸轮上作用未知力F ，如图所示。
如果轴平衡，求力F 和轴承约束力。
解：取水平轴及两个凸轮为研究对象，受力如图（b ）所示。
列平衡方程N80002.02.0,0)(11===⨯+⨯-=∑F F F F M yF)N(3204.08004.004.01,0)(↓-=⨯-=⨯-==⨯+⨯=∑F F F F MBz Bz xFN11204.18004.104.11,0)(11=⨯=⨯==⨯-⨯=∑F F F F MBx Bx zFN32080011200,011=-=-==+-=∑F F F F F F FBx Ax Bx Ax x)N(480800)320(0,0↓-=---=--==++=∑F F F F F F FBz Az Bz Az z4-13 小车C 沿斜面匀速上升，已知小车重W 1=10kN ，鼓轮重W =1kN ，四根杠杆的臂长相同且均垂直于鼓轮轴，其端点作用有大小相同的力F 1、F 2、F 3及F 4。
