五年级奥数--巧求周长

小学五年级奥数知识点分类汇总及解析第3讲长方形、正方形的周长一、知识要点同学们都知道,长方形的周长=(长+宽)×2.正方形的周长=边长×4。

长方形、正方形的周长公式只能用来计算标准的长方形和正方形的周长。

如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长,还需同学们灵活应用已学知识,掌握转化的思考方法,把复杂的问题转化为标准的图形,以便计算它们的周长。

二、精讲精练【例题1】有5张同样大小的纸如下图(a)重叠着,每张纸都是边长6厘米的正方形,重叠的部分为边长的一半,求重叠后图形的周长。

【思路导航】根据题意,我们可以把每个正方形的边长的一半同时向左、右、上、下平移(如图b),转化成一个大正方形,这个大正方形的周长和原来5个小正方形重叠后的图形的周长相等。

因此,所求周长是18×4=72厘米。

练习1:1.下图由8个边长都是2厘米的正方形组成,求这个图形的周长。

2.下图由1个正方形和2个长方形组成,求这个图形的周长。

3.有6块边长是1厘米的正方形,如例题中所说的这样重叠着,求重叠后图形的周长。

【例题2】一块长方形木板,沿着它的长度不同的两条边各截去4厘米,截掉的面积为192平方厘米。

现在这块木板的周长是多少厘米?【思路导航】把截掉的192平方厘米分成A、B、C三块(如图),其中AB的面积是192-4×4=176(平方厘米)。

把A和B移到一起拼成一个宽4厘米的长方形,而此长方形的长就是这块木板剩下部分的周长的一半。

176÷4=44(厘米),现在这块木板的周长是44×2=88(厘米)。

练习2：1.有一个长方形,如果长减少4米,宽减少2米,面积就比原来减少44平方米,且剩下部分正好是一个正方形。

求这个正方形的周长。

2.有两个相同的长方形,长是8厘米,宽是3厘米,如果按下图叠放在一起,这个图形的周长是多少?3.有一块长方形广场,沿着它不同的两条边各划出2米做绿化带,剩下的部分仍是长方形,且周长为280米。

数学头脑风暴个性化学案学生姓名：年级：巧求周长同学们都知道，长方形的周长=（长＋宽）×2，正方形的周长=边长×4。

长方形、正方形的周长公式只能用来计算标准的长方形和正方形的周长。

如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长，还需同学们灵活应用已学知识，掌握转化的思考方法，把复杂的问题转化为标准的图形，以便计算它们的周长。

例1 有5张同样大小的纸如下图（a）重叠着，每张纸都是边长6厘米的正方形，重叠的部分为边长的一半，求重叠后图形的周长。

分析与解答：练习一1．下图由8个边长都是2厘米的正方形组成，求这个图形的周长。

2．下图由1个正方形和2个长方形组成，求这个图形的周长。

3．有6块边长是1厘米的正方形，如例题中所说的这样重叠着，求重叠后图形的周长。

例2 一块长方形木板，沿着它的长度不同的两条边各截去4厘米，截掉的面积为192平方厘米。

现在这块木板的周长是多少厘米？分析与解答：练习二1．有一个长方形，如果长减少4米，宽减少2米，面积就比原来减少44平方米，且剩下部分正好是一个正方形。

求这个正方形的周长。

2．有两个相同的长方形，长是8厘米，宽是3厘米，如果按下图叠放在一起，这个图形的周长是多少？3．有一块长方形广场，沿着它不同的两条边各划出2米做绿化带，剩下的部分仍是长方形，且周长为280米。

求划去的绿化带的面积是多少平方米？例3 已知下图中，甲是正方形，乙是长方形，整个图形的周长是多少？分析与解答：练习三1．有一张长40厘米，宽30厘米的硬纸板，在四个角上各剪去一个同样大小的正方形后准备做一个长方体纸盒，求被剪后硬纸板的周长。

2．一个长12厘米，宽2厘米的长方形和两个正方形正好拼成下图所示长方形，求所拼长方形的周长。

3．求下面图形的周长（单位：厘米）。

例4 下图是边长为4厘米的正方形，求正方形中阴影部分的周长。

分析与解答：练习四1．求下面图形的周长（单位：厘米）。

小学五年级下册奥数题型分类讲义(附答案)图形问题专题1长方形、正方形的周长一、专题解析同学们都知道，长方形的周长=（长＋宽）×2，正方形的周长=边长×4.长方形、正方形的周长公式只能用来计算标准的长方形和正方形的周长。

那么如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长呢？还需同学们灵活应用已学知识，掌握转化的思考方法，把复杂的图形转化为标准的图形，以便计算它们的周长。

二、精讲精练例题1】有5张同样大小的纸如下图（a）重叠着，每张纸都是边长6厘米的正方形，重叠的部分为边长的一半，求重叠后图形的周长。

思路导航】根据题意，我们可以把每个正方形的边长的一半同时向左、右、上、下平移（如图b），转化成一个大正方形，这个大正方形的周长和原来5个小正方形重叠后的图形的周长相等。

因此，所求周长是18×4=72厘米。

操演11、右图由8个边长都是2厘米的正方形组成，求这个图形的周长。

2、右图由1个正方形和2个长方形组成，下方长方形长为50cm，求这个图形的周长。

3、有6块边长是1厘米的正方形，如例题中所说的这样重叠着，求重叠后图形的周长。

1例题2】一块长方形木板，沿着它的长度不同的两条边各截去4厘米，截掉的面积为192平方厘米。

现在这块木板的周长是多少厘米？思路导航】把截掉的192平方厘米分红A、B、C三块（如图），个中AB的面积是192－4×4=176（平方厘米）。

把A和B移到一同拼成一个宽4厘米的长方形，而此长方形的长就是这块木板剩下部分的周长的一半。

176÷4=44（厘米），现在这块木板的周长是44×2=88（厘米）。

练21、有一个长方形，如果长减少4米，宽减少2米，面积就比原来减少44平方米，且剩下部分恰好是一个正方形。

求这个正方形的周长。

2、有两个相同的长方形，长是8厘米，宽是3厘米，如果按下图叠放在一起，这个图形的周长是几何？3、有一块长方形广场，沿着它不同的两条边各划出2米做绿化带，剩下的部分仍是长方形。

第3讲长方形、正方形的周长一、知识要点同学们都知道，长方形的周长=（长＋宽）×2.正方形的周长=边长×4。

长方形、正方形的周长公式只能用来计算标准的长方形和正方形的周长。

如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长，还需同学们灵活应用已学知识，掌握转化的思考方法，把复杂的问题转化为标准的图形，以便计算它们的周长。

二、精讲精练【例题1】有5张同样大小的纸如下图（a）重叠着，每张纸都是边长6厘米的正方形，重叠的部分为边长的一半，求重叠后图形的周长。

练习1:1.下图由8个边长都是2厘米的正方形组成，求这个图形的周长。

2.下图由1个正方形和2个长方形组成，求这个图形的周长。

【例题2】一块长方形木板，沿着它的长度不同的两条边各截去4厘米，截掉的面积为192平方厘米。

现在这块木板的周长是多少厘米？练习2：1.有一个长方形，如果长减少4米，宽减少2米，面积就比原来减少44平方米，且剩下部分正好是一个正方形。

求这个正方形的周长。

2.有两个相同的长方形，长是8厘米，宽是3厘米，如果按下图叠放在一起，这个图形的周长是多少？【例题3】已知下图中，甲是正方形，乙是长方形，整个图形的周长是多少？练习3：1.有一张长40厘米，宽30厘米的硬纸板，在四个角上各剪去一个同样大小的正方形后准备做一个长方体纸盒，求被剪后硬纸板的周长。

2.一个长12厘米，宽2厘米的长方形和两个正方形正好拼成下图（1）所示长方形，求所拼长方形的周长。

【例题4】下图是边长为4厘米的正方形，求正方形中阴影部分的周长。

练习4：1.求下面图形的周长（单位：厘米）。

4cm8cm2.在（）里填上“＞”、“＜”或“=”。

甲的周长（）乙的周长【例题5】如下图，阴影部分是正方形，DF=6厘米，AB=9厘米，求最大的长方形的周长。

练习5：1.下面三个正方形的面积相等，剪去阴影部分的面积也相等，求原来正方形的周长发生了什么变化？（单位：厘米）2.下面是一个零件的平面图，图中每条短线段都是5厘米，零件长35厘米，高30厘米。

一、基本概念①周长：封闭图形一周的长度就是这个图形的周长． ②面积：物体的表面或封闭图形的大小，叫做它们的面积．二、基本公式：①长方形的周长2=⨯(长+宽)，面积=长⨯宽．②正方形的周长4=⨯边长，正方形的面积=边长⨯边长．三、常用方法：（1）对于基本的长方形和正方形图形，可以直接用公式求出它们的周长和面积，对于一些不规则的比较复杂的几何图形，我们可以采用转化的数学思想方法割补成基本图形，利用长方形、正方形周长及面积计算的公式求解．（2）转化是一种重要的数学思想方法，在转化过程中要抓住“变”与“不变”两个部分．转化后的图形虽然形状变了，但其周长和面积不应该改变，所以在求解过程中不能遗漏掉某些线段的长度或某部分图形的面积．转化的目标是将复杂的图形转化为周长或面积可求的图形．（3）寻求正确有效的解题思路，意味着寻找一条摆脱困境、绕过障碍的途径．因此，我们在解决数学问题时，思考的着重点就是要把所需解决的问题转化为已经能够解决的问题．也就是说，在直接求解不容易或很难找到解题途径的问题时，我们往往转化问题的形式，从侧面或反面寻找突破口，知道最终把它转化成一个或若干个能解决的问题．这种解决问题的思想在数学中叫“化归”，它是数学思维中重要的思想和方法．（4）在几何中，有许多图形是由一些基本图形组合、拼凑而成的．这样的图形我们称为不规则图形．不规则图形的面积往往无法直接应用公式计算．那么，不规则图形的面积怎样去计算呢？对称、旋转、平移这几种几何变换就是解决这类面积问题的手段．四、几个重要的解题思想 （1）平移在平面图形的计算中，常常要将一个平面图形移动到平面上的另一个位置进行计算．其中，将图形沿一个固定方向的移动叫做平移，一个图形经过平行移动不改变其形状与大小，所以图形面积是保持不变的．利用图形的平移，可以使面积计算问题的解法简捷明快，颇有新意．知识点拨4-2-2.巧求周长（2）割补割补法在我国古代叫“出入相补原理”，我国古代魏晋时期著名的数学家刘徽在《九章算术注》中就明确地提出“出入相补，各从其类”的出入相补原理．这个原理的内容是几何图形经过分、合、移、补所拼凑成的新图形，它的面积不变．（3）旋转在平面图形的割补中，有时要将一个图形绕定点旋转到一个新的位置，产生一种新的图形结构，图形在转动过程中形状大小不发生改变．利用这种新的图形结构可以帮我们解决面积的计算问题．（4）对称平面图形中有许多简单漂亮的图形都是轴对称图形．轴对称图形沿对称轴折叠，轴两侧可以完全重合．也就是说，如果一个图形是轴对称图形，那么对称轴平分这个图形的面积．熟悉轴对称图形这个性质，对面积计算会有很大帮助．（5）代换在几何计算中，对有关数量进行适当的等量代换也是解决问题的已知技巧．小结：本讲主要通过求一些不规则图形的周长，体会一种转化思想，重点在于把不规则图形转化为规则图形的方法，包括平移、旋转、割补、差不变原理，通过这些方法的学习，让学生体会求周长的技巧，提高学生的观察能力、动手操作能力、综合运用能力．例题精讲模块一、图形的周长和面积——割补法【例1】求图中所有线段的总长(单位：厘米)D【考点】巧求周长【难度】2星【题型】填空【解析】要注意到，题目所求的是图中所有线段的总长，而图中的线段，并不仅仅是AB、BC、CD、DE四段，还包括AC、BE等等，因此不能简单地将图中标示的线段长度进行求和．同时应该注意到，BE BC CD DE，等等．因此，为了计算图中所有线段的=++=++=AC AB BC；3126=+=+43总长，需要先计算AB、BC、CD、DE这四条线段分别被累加了几次．这里，可以按照每条线段分别是由几部分组成的加以讨论：由1段组成的线段共有4条，即AB、BC、CD、DE，而求和过程中AB、BC、CD、DE这四条线段各被累加了1次．类似地考虑到，由2段组成的线段共有3条，求和过程中AB、DE各被累加了1次, BC、CD各被累加了2次．由3段组成的线段共有2条，求和过程中AB、DE各被累加了1次，BC、CD各被累加了2次．由4段组成的线段只有AE，其中AB、BC、CD、DE各被计算了1次．综上所述，AB、DE各被计算了4次，BC、CD各被计算了6次．因而图中所有线段的总长度为：()()⨯++⨯+（厘米）442631=48【答案】48【例2】如图所示，点B是线段AD的中点，由A、B、C、D四个点所构成的所有线段的长度均为整数，若这些线段的长度之积为10500，则线段AB的长度是。

巧求周长与面积掌握巧求周长与面积的基本方法；1. 理解并掌握割补、平移等数学思想方法。

【例1】 （2007年“希望杯”第一试）右图中的阴影部分BCGF 是正方形，线段FH 长18厘米，线段AC 长24厘米，则长方形ADHE 的周长是__________厘米。

【分析】 由于图中阴影部分BCGF 是个正方形，其四条边的边长都相等，且等于长方形ADHE 的宽。

FH AC +的和应为长方形ADHE 的长加上正方形BCGF 的边长，所以等于长方形ADHE 的长与宽之和。

所以长方形ADHE 的周长为：(1824)284+⨯=厘米。

【例2】 如右图所示，在一个正方形内画中、小两个正方形，使三个正方形具有公共顶点，这样大正方形被分割成了正方形区域甲，和L 形区域乙和丙。

甲的边长为4厘米，乙的边长是甲的边长的1.5倍，丙的边长是乙的边长的1.5倍，那么丙的周长为多少厘米？EF 长多少厘米？【分析】 乙的周长实际上是正方形AHJE 的周长（我们可将乙与甲重合的两条线段分别向左、向下平移），同样的，丙的周长也就是正方形ABCD 的周长。

由于4 1.56AE =⨯=，6 1.59AD =⨯=，所以丙的周长为9436⨯=厘米，642EF AE AF =-=-=（厘米）。

【例3】 用若干个边长都是2厘米的平行四边形与三角形（如右图）拼接成一个大的平行四边形，已知大平行四边形的周长是244厘米，那么平行四边形和三角形各有多少个？【分析】 大平行四边形上、下两边的长为(24422)2120-⨯÷=厘米，观察上边，每6厘米有两个平行四边形的边，所以共有小平行四边形1206240÷⨯=个，三角形的数量与小平行四边形的数量相等，也是40个。

[拓展] 用若干个边长都是2厘米的平行四边形与三角形（如右图）拼接成一个大的平行四边形，已知大平行四边形的周长是236厘米，那么平行四边形和三角形各有多少个？[分析] 大平行四边形上、下两边的长为(23622)2116-⨯÷=厘米，观察上边，每6厘米有两个平行四边形的边，1166192÷=L ，所以有三角形19238⨯=个，小平行四边形38139+=个。

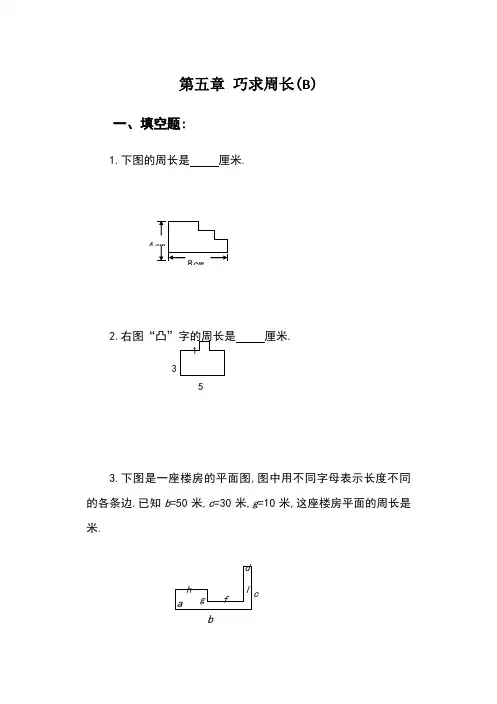
第五章 巧求周长(B )一、填空题:1.下图的周长是 厘米.2.右图“凸”字的周长是 厘米.3.下图是一座楼房的平面图,图中用不同字母表示长度不同的各条边.已知b =50米,c =30米,g =10米,这座楼房平面的周长是 米.453bc4.下图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是 厘米.5.下图“E ”字周长是 厘米.()6.下图由5个边长8厘米的小正方形拼成的“T ”字形,它的周长是 厘米.337.下图是一“环球游戏探险的隧道”的平面图,一儿童沿隧道周游一周,8下图是由10个边长为3厘米的小正方形组成.每个小正方形的顶点恰在另一个正方形的中心,且边相互平行,求这个图形的周长.50单位: 米339.把一块长20厘米,宽12厘米的长方形纸按右下图所示方法一层、二层、三层的摆下去,共要摆十层,摆好后图形周长是 厘米.10.下图是一个零件的平面图,图中每一条最短线段均长5厘米.零件长35厘米,高30厘米,这个零件周长是多少厘米二、解答题11.下图是一个“干”字形图形.已知两横均由长6厘米,宽1厘米的长方形构成,中间一竖是由长6厘米,宽2厘米的长方形构成,3012.在4cm7cm 的正方形网格(如图)中,所有正方形的周长的和是多少cm13.如下图所示,长方形长4厘米,宽2厘米.现沿其对角线BD 对折得到一几何图形,试求图形阴影部分周长.14.如图,在长方形ABCD 中,EFGH 是正方形.如果AF =10厘 D E F米,HC =7厘米,那么长方形ABCD 的周长是 厘米———————————————答 案——————————————————————1. (8+4)2=122 =24(厘米)经过平移线段,把原图形变成长是8cm ,宽是4cm 的长方形.2. 18厘米如图我们发现,它不是一个规则的正方形或长方形,所以不能A BD E F G H直接套用公式.但如我们把线段AC 放在C A ''、C C '放在A A '、DB 放在B D ''、D D '放在B B '的位置,则此图就变成一个正规的长方形,如下图所示.[5+(3+1)]×2=9×2=18(厘米)答:周长18厘米.3. 180米平移线段得到一个长是50米,宽是30米的长方形,还剩两段如图所示,所以周长是(50+30)2+210=180(米)35 A BC DA '' C ' D '1g c b4. 170厘米每个小正方形的面积为40016=25平方厘米.所以每个小正方形的边长是5cm ,因此它的周长是345=170厘米. 5. 20厘米为了分析方便,我们把图如下编号,则图形变成下列形式.我们把a 移至a '处,把b 移至b '处，图形成为一个大正方形里有4条2厘米长的线段，求“E ”形周长就很简单了.解:34+24=12+8 =20(厘米)答:这个“E ”字形的周长是20厘米.6. 96厘米求“T ”字形的周长即求下图的周长,经过平移得一边长为(83=)24厘米的正方形.所以周长为244=96(厘米) '' b a7. 304米我们不妨把有关线段用字母编号(如图所示)观察可知,我们只需把a 平移至a ',把g 平移至g ',把h 平移至h ',就可以得到一个规则的长方形,但我们发现线段b 、c 、f 及d 、e 的长度尚末计算,又发现如b +c 的长度正好等于f 等于40米,而e 或d 分别为2米,总共为402+22=84(米)再加上原长方形的周长(50+60)2=220米即为此图周长. 解:(50+60)2+402+22 =1102+80+4 60米 50米40米 2米 a b c d e f h g a ' b ' '=220+80+4=304(米)答:此图周长为304米.8. 66厘米此题如仍用平移的方法,不仅移动的次数多且较为麻烦,不妨我们分水平方向和竖直方向两种分别讨论,水平方向上有(3+9)2=33厘米,同理,竖直方向也为(3+9)2=33厘米,周长可求.解:(3+9)22=332=66(厘米)答:此图形周长为66厘米.9. 先观察此图,第一层有一个长方形,第二层有两个长方形,第三层有三个长方形……第十层应有十个长方形,我们仍利用如前所述平移线的方法,我们发现它可移成一个长为2010=200厘米、宽为1210=120厘米的规则长方形,周长也不难求得了.解:(2010+1210)2=(200+120)2=3202=640(厘米)答:这个图形的周长为640厘米.10. 我们把图形按下图所示方向移动,而对于零件下方的“十”字,则可把“十”字上面的横线移下来,这时,使图形成为一个大长方形,再看长方形里有小线段10条,而每条都长5厘米,所以题目得解.30厘米35厘米解:(35+30)2+510=652+50=130+50=180(厘米)答:这个图形的周长是180厘米.11. 为说明方便,我们把有关线段标上字母,从图中可看出如把a 、b 、c 、d 、e 、f 线段分别移至a 'b 'c 'd 'e 'f '处,如图:这时,图形变成为一个边长为6厘米的大正方形里有4条长为(6-2)÷2=2(厘米)的横线,求周长便容易了.6×4+(6-2)÷2×4=24+2×4=32(厘米)12. 解 分类进行统计,得:边长为1cm 的正方形周长的和是14(47)=112(cm ); 边长为2cm 的正方形周长的和是:24(36)=144(cm ); 边长为3cm 的正方形周长的和是:34(25)=120(cm ); 1 12 3 61 a b c d e f a c ' f '边长为4cm的正方形周长的和是:44(14)=64(cm);图中所有正方形周长的和是:112+144+120+64=440(cm).13. 把图中△BDE以BD为轴再转回去,使之与△ADB完全重合,不难看出要求的阴影部分的周长正好等于长方形的周长.阴影部分周长由BE+ED+DC+BC而BE=AB、DE=AD.所以阴影部分周长为AD+AB+BC+DC=(4+2)2=62=12厘米.(4+2)2=62=12(厘米)答:它的周长为12厘米.14. 由题目已知条件可知:四边形EHCB,ADGF都是矩形.所以EB=HC=7(厘米).AD=FG=EF.由以上分析结果,AB+AD=AB+EF.因为AB=AF+FB,所以AB+AD=AF+FB+EF=AF+EF+FB=AF+EB=10+7=17(厘米).所以长方形ABCD的周长=172=34(厘米).。

求楼梯(红地毯)的长度也可直接用3+2=5(米)而不必套用长方形周长公式.
[拓展]如下图，你能求出这个图形的周长吗？
分析：如果所示，通过平移原图形就转化为一个长方形了.这个长方形的周长与这个不规则图形的周长相等.
列式：(3×7+2×7)×2=70(分米)；这个图形的周长是70分米.
【例3】（★★★★奥数网题库）下图是一个正方形操场，它的边长是100米，甲同学沿着甲块地走了一圈，乙同学沿着乙块地走了一圈，谁走的路长?为什么?他们各走了多少米?
(4)图中两个字的周长一共是：120＋24＝144(厘米)
方法2：图中“土”字的周长等于24条3厘米长的线段的和；“山”字的周长也正好等于24条3厘米长的线段的和.所以，“土山”这两个字的周长就等于24条3厘米长的线段的和的2倍.
法2： 3×24×2＝72×2＝144(厘米)或3×24＋3×24=144（厘米）
分析：方法1：根据转化的思考方法，把图8转化为图9(箭头所指的是转化的部分)后，原图只有画“○”的线段没有转化.这样，图中两个字的周长就转化为两个大正方形的周长与8条3厘米长的线段的和.
法1(1)图中大正方形的边长：3×5＝15(厘米)
(2)图中两个大正方形周长的和是：5×4×2＝120(厘米)
(3)图中画“○”的8条线段的总长是：3×8＝24(厘米)
分析：这道题关键在于求楼梯的长度.虽然题目并没有给出每层台阶的高度和宽度，但是，如果把每层台阶的宽度移到和最上层台阶一样高的地方；把每层台阶的高度向右而楼梯的长不就是长方形周长的一半吗?所以楼梯的长等于(3+2)×2÷2=5米，红地毯每米80元，5米应是80×5=400元.
长方形的另一条边长为c＋l＝70＋250＝320(米)所以图2中长方形的周长为(320＋310)×2＝1260(米)，所以每天跑的米数为1260×3＝3780(米)

长方形、正方形的周长［知识要点］同学们都知道，长方形的周长=（长＋宽）×2，正方形的周长=边长×4。

长方形、正方形的周长公式只能用来计算标准的长方形和正方形的周长。

如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长，还需同学们灵活应用已学知识，掌握转化的思考方法，把复杂的问题转化为标准的图形，以便计算它们的周长。

［范例解析］例1有5张同样大小的纸如下图（a）重叠着，每张纸都是边长6厘米的正方形，重叠的部分为边长的一半，求重叠后图形的周长。

思路与导航根据题意，我们可以把每个正方形的边长的一半同时向左、右、上、下平移（如图b），转化成一个大正方形，这个大正方形的周长和原来5个小正方形重叠后的图形的周长相等。

因此，所求周长是18×4=72厘米。

例2 一块长方形木板，沿着它的长度不同的两条边各截去4厘米，截掉的面积为192平方厘米。

现在这块木板的周长是多少厘米？思路导航把截掉的192平方厘米分成A、B、C三块（如图），其中AB的面积是192－4×4=176（平方厘米）。

把A和B移到一起拼成一个宽4厘米的长方形，而此长方形的长就是这块木板剩下部分的周长的一半。

176÷4=44（厘米），现在这块木板的周长是44×2=88（厘米）。

例3求下列图形的周长。

（单位：厘米）思路导航：从图中可以看出，整个图形的周长由八条线段围成，其中四条横着，四条竖着。

其中上面三条横着的线段和是10厘米，那么这样四条横着的线段和是10+10=20（厘米），四条竖着的线段和是8×2+2×2=20（厘米）。

所以，整个图形的周长是20+20=40（厘米）。

例4下图是边长为4厘米的正方形，求正方形中阴影部分的周长。

例5 如下图，阴影部分是正方形，DF=6厘米，AB=9厘米，求最大的长方形的周长。

分析根据题意可知，最大长方形的宽就是正方形的边长。

因为BC=EF，CF=DE，所以，AB＋BC＋CF=AB＋FE＋ED=9＋6=15（厘米），这正好是最大长方形周长的一半。

小学数学《巧求周长和面积》练习题（含答案）“巧求周长和面积”的相关内容我们在寒假小4第四讲给予过一定的讲解. 本讲我们主要在原有知识的基础上进行提高巩固，同时加入一些新的知识，帮助我们更好的过渡到五年级几何部分的学习. 对于一些非常典型的例题，我们采用“重复加强”的学习方法，帮助孩子们牢固掌握. 奥数的题目虽然很多，但一些经典题目，常常会以原题形式出现在各个中学入学测试题中，希望我们的孩子能戒骄戒躁，温故而后知新，清晰彻底的掌握理解自己学习过题目.你还记得吗【复习1】若干个长2cm、宽1cm的长方形摆成如右图的形状，求该图形的周长.分析：观察图形，上下共有13层，所以左、右的高共长：1×13×2=26(cm)；从下层往上数，第四层最长，有2×10=20cm，所以上下的宽共有：20×2=40(cm)，故该图形的周长为：26+40=66(cm) .【复习2】右图中是一个方形螺线.已知两相邻平行线之间的距离均为l厘米，求螺线的总长度.分析：如下图所示，将原图形转化为3个边长分别为3、5、7厘米的正方形和中间一个三边图形.所以螺线的总长度为：（3+5+7）×4+1×3=63 cm .【复习3】有10张长3厘米，宽2厘米的纸片，将它们按照右图的样子摆放在桌面上，那么这10张纸片所盖住的桌面的面积是多少平方厘米？分析：每多盖一张，遮住的面积增加2×1，所以这10张纸片所盖住的桌面的面积是3×2+2×1×9=24cm2.巧求周长【例1】图1、图2都是由完全相同的正方形拼成的，并且图1的周长是22厘米，那么图2的周长是多少厘米？分析：图1的周长是小正方形边长的12倍。

图2的周长是小正方形边长的18倍．因此，图2的周长=22÷12×18=33(厘米)【巩固】右图是由16个同样大小的正方形组成的，如果这个图形的面积是400平方厘米，那么它的周长是多少厘米?分析：因为400÷16=25(平方厘米)，所以每个正方形的边长是5厘米.观察右图，从上下方向来看有14条边是周长的一部分，从左右方向来看有20条边是周长的一部分，所以周长为170厘米.【例2】计算右面图形的周长(单位：厘米).分析：要求这个图形的周长，似乎不可能，因为缺少条件.但是，我们仔细观察这个图形，发现它的每一个角都是直角，所以，我们可以将图中右上缺角处的线段分别向上、向右平行移动到虚线处(见右下图)，这样正好移补成一个长方形。

五年级奥数举一反三
【例题3】 已知下图中，甲是正方形，乙是长方形，整 个图形的周长是多少？
【思路导航】
从图中可以看出，整个图形的周长由六条线段围成，其中三条横着， 三条竖着。三条横着的线段和是（a＋b）×2，三条竖着的线段和是 b×2。所以，整个图形的周长是（a＋b）×2＋b×2，即2a＋4b。
五年级奥数举一反三
图一
图二 图三
五年级奥数举一反三
【例题5】
如下图，阴影部分是正方形，DF=6厘米，AB=9厘米，求 最大的长方形的周长。
【思路导航】 根据题意可知，最大长方形的宽就是正方形的边长。因 为BC=EF，CF=DE，所以，AB＋BC＋CF=AB＋FE＋ED=9＋ 6=15（厘米），这正好是最大长方形周长的一半。因此， 最大长方形的周长是（9＋6）×2=30（厘米）。
【练习2】
1，有一个长方形，如果长减少4米，宽减少2米，面积就比原来减少44 平方米，且剩下部分正好是一个正方形。求这个正方形的周长。
2，有两个相同的长方形，长是8厘米，宽是3厘米，如果按下图叠放在 一起，这个图形的周长是多少？

3，有一块长方形广场，沿着它不同的两条边各划出2米做绿化带，剩下 的部分仍是长方形，且周长为280米。求划去的绿化带的面积是多少平 方米？
五年级奥数举一反三
【例题1】 有5张同样大小的纸如下图（a）重叠着， 每张纸都是边长6厘米的正方形，重叠的部分 为边长的一半，求重叠后图形的周长。
五年级奥数举一反三
【思路导航】 根据题意，我们可以把每个正方形的边长 的一半同时向左、右、上、下平移（如图b）， 转化成一个大正方形，这个大正方形的周长 和原来5个小正方形重叠后的图形的周长相等。 因此，所求周长是18×4=72厘米。

小学奥数巧求周长练习题及答案一、填空1.下图是一块地,四周都用篱笆围起来,转弯处都是直角.已知西边篱笆长17米,南边篱笆长23米.四周篱笆长 米.2.求下图周长.单位:厘米3.下图是一个公园的平面图,A 是公园的大门.问:小明从A 门进公园,不重复地沿道路走公园一圈,他走了多少米?4.下图是某建设物的设计图,如图所示(单位:米)现根据需要在它周围绕电线一圈,试求需电线多少米?5.用15个边长2厘米的小正方形摆成如下图的形状,求图形周长是多少厘米?6.下图是一块小麦地,已知条件如图中所示.这块地的周长是 米.501 1 1 1 12 33 4 4240A7.下图“十”字的横与竖都长6厘米.问“十”间的周长是 厘米.8.求下图上“凹”形的周长.单位:厘米9.下图是由若干个相等的正方形组成的“土山”两个字,已知每个正方形的边长是3厘米,这两个字的周长分别是 、 厘米.10.下图是由三个相同的长方形纸片组成的一个“5”字,已知长方形长4厘米,宽2厘米,“5”字周长是 厘米.二、解答题11.把边长分别是5厘米、4厘米、3厘米和2厘米的4个正方形按从大到小的顺序排成一行(如图),排成的图形周长是多少厘米?12.将一张边长为12厘米的正方形纸对折,再将对折后的纸沿它的竖直中线(右图虚纸)剪开,得到三个矩形纸片,?13.一个正方形被分成了5个相等的长方形.每个长方形的周长都是40厘米,求正方形的周长是多少厘米?如图所示.14.如图正方形ABCD 的边长为4cm,每边被四等分.求图中所有正方形周长的和.———————————————答 案——————————————————————1. 80米经过线段平移,原图形可变为长是23米,宽是17米的长方形,所以周长为(23+17)⨯2=80(米).2. 218厘米为分析叙述方便,我们如图所示编上字母,我们可把a 移至、b 移至、c 移至、d 移至,这样厘米,所以图中所有的横线的长是50⨯2=100厘米,图中所有竖线的长为40+5+15⨯2+4+40-(5-4)=118(厘米)则整个图形周长可求.解:50⨯2+40+5+15⨯2+4+40-(5-4)=100+118=218(厘米)答:这个图形的周长为218厘米.3、我们把与分析题有关的线段编号,如图:我们可把移到,移到位置,把移到,移到,把移到,把移到,则此图变成为一个规则的长方形,它的长是360米,宽是240米,周长可求:即(360+240)⨯2=1200(米).4. 40米 我们如图所示将有关线段标上字母,将a 、b 、c 、d 、e 、f 、g 、h 、i 、j 、k 、l 、m 分别移至相对应处,即、、、、、、、、、、、、的位置，其中还有两段末移动，再加上这两段和移动后拼成的长方形即为本图周长.解:(4+2+4+1+1+1+3)⨯2+(3+1)⨯2=16⨯2+4⨯2=40(米)1`答:需电线40米.5. 48厘米我们可从水平方向和竖直方向分析此题,在水平方向上,所有线段的长度和为9⨯2⨯2=36厘米,在竖直方向上,所有线段的长度为3⨯2⨯2=12厘米.因此,此图形周长可求.解:9⨯2⨯2=18⨯2=36(厘米)3⨯2⨯2=6⨯2=12(厘米)36+12=48(厘米)答:它的周长为48厘米.360米A6、200米经过平移线段原图可转化为一边长为50米的正方形,所以周长50⨯4=200(米).7. 24厘米从图中可看出,“十”字的周长是由12条相等的线段组成,而题目又告诉我们,“横竖都长6厘米”,可知每3条相等的线段长度的和是6厘米,于是可求出“十”字的周长,当然,我们也可把“十”中竖的上、下两个横放置中间，同理横的左右两个竖放置中间变成如下图所示：这样,每条线段均长6厘米,也不难求出“十”的周长.解法一:6⨯(1⨯12÷3)=6⨯4=24(厘米)答:这个“十”的周长是24厘米.解法二:6⨯4=24(厘米)答:这个“十”的周长是24厘米.8. 18厘米我们可把它转化一下,变成下图所示:这时,解法就同B 卷第2题一样了.解:[5+(3+1)]⨯2=[5+4]⨯2=9⨯2=18(厘米)9. 72厘米、72厘米分析:图中“土”字的周长等于24条3厘米长的线段的和;“山”字的周长也正好等于24条3厘米长的线段的和.所以,“土山”这两个字的周长分别等于24条3厘米长的线段的和.3⨯24=72(厘米)答:这两个字的周长分别是72厘米.10. 28厘米我们可按下图所示方向把ab 移到、移到，把cd 移到、把移到的位置,则此厘米,宽边为4+2=6厘米,它的周长可求.答:此图形的周长为28厘米.解:(4+2+2+4+2)⨯2=14⨯2=28(厘米)11. 平移线段,可把原图形变为一个标准长方形如下图所示:显然该长方形的长是(5+4+3+2)=14(厘米),宽是5厘米,所以周长是(14+5)⨯2=38(厘米)12. 分析与解:根据题目条件可知两个较小的长方形的周长相同.小矩形的长=12(厘米)小矩形的宽=12÷2÷2=3(厘米)小矩形的周长=(12+3)⨯2=30(厘米)两个小矩形的周长=30⨯2=60(厘米)答:其中两个较小矩形的周长之和是60厘米.13. 因为每个小长方形的周长都是40厘米,所以每个小长方形的一个长与一个宽的和为:40÷2=20厘米.因为5个小长方形的宽等于小长方形的长(或大正方形的边长)所以20厘米是6个小长形的宽,而1个小长方形的长应为20÷6⨯5,所以大正方形周长可求.方法一:解:40÷2÷6⨯5⨯4=20÷6⨯5⨯4≈66.7(厘米)答:周长为66.7厘米.方法二:每个小长方形的周长都是40厘米,这时我们再把正方形用横线平均分成5个相等的长方形(如下图).5432很明显,每小格都是相等的小正方形. 由图可知小长方形都是由5个这样的小格组成,则每个小长方形的周长是由12条小正方形的边长组成的.则小正方形的边长为40÷12≈3.厘米.这时就可求小长方形的长是3.33⨯5=16.65厘米.那么我们就可以求出大正方形的周长是:16.65⨯4=66.6(厘米)答:正方形的周长是66.6厘米.14. 解分类进行统计,得:边长为1cm的正方形周长的和是:1⨯4⨯(4⨯4)=64(cm);边长为2cm的正方形周长的和是:2⨯4⨯(3⨯3)=72(cm);边长为3cm的正方形周长的和是:3⨯4⨯(2⨯2)=48(cm);边长为4cm的正方形周长的和是:4⨯4⨯(1⨯1)=16(cm);图中所有正方形周长的和是:64+72+48+16=200(cm);。

第一讲巧求周长知识导航一、周长的基本概念周长：封闭图形一周的长度就是这个图形的周长。

二、周长的基本公式1.长方形的周长=（长+宽）×22.正方形的周长=边长×4三、计算周长的常用方法1.对于基本的长方形和正方形图形，可以直接用公式求出它们的周长和面积2.对于一些不规则的比较复杂的几何图形，我们可以采用转化的数学思想方法割补成基本图形，利用长方形、正方形的周长及面积的计算公式求解。

典型例题一（基本图形的周长）例1 下图由1个长方形和2个三角形拼成，线段长度如图所标，求图形的周长。

练习：如果所示，一个大长方形被三条线段分成了四个小长方形，各条线段长度已经标在图中。

求图中所有长方形的周长之和。

典型例题二（移补法求复杂图形的周长）例2 求如图所示的图形的周长。

（单位：厘米）练习如图所示，求图形的周长。

（单位：厘米）典型例题三（其他方法求复杂图形的周长）例3 下图中的阴影部分BCGF是正方形，线段FH长28厘米，线段AC长34厘米，则长方形ADHE的周长是多少厘米？练习如图所示，长方形ABCD被线段EG，HF分割成4个更小的长方形，已知长方形AEOH的周长为18厘米，CGOF的周长为16厘米，BFOE的周长为26厘米，求长方形ABCD的周长和长方形DHOG的周长。

课后巩固1．如图所示是由2个正方形和1个三角形组成的图形，线段长度见图中所标注，求该图形的周长。

（单位：厘米）2．如图所示，正方形ABCD的边长是6厘米，过正方形内的两点画直线，可把正方形分成9个小长方形。

这9个小长方形的周长之和是多少厘米？3．如图所示，是一个机器零件的侧面图，图中每一条最短线段长5厘米，这个零件高30厘米，求这个零件侧面的周长。

4．如图所示，在长方形ABCD中，EFGH是正方形。

已知AF的长为11厘米，HC的长为8厘米，求长方形ABCD的周长。

5．根据图中已标出线段的长度求如图所示图形的周长。

（单位：厘米）6．如图所示，用8个相同的长方形板砌成一个正方形边框。

1．周长：围城一个图形的所有边长的总和就是这个图形的周长2．长方形周长＝表示长方形的周长，a表示长方形的长，表示长方形的宽，则长方形的周长可以写成3．正方形的周长＝边长×表示正方形的周长表示正方形的边长则正方形的周长可以周长，a表示正方形的边长，则正方形的周长可以5．不规则图形→⑴平移：平行移动长度不变⑴平移平行移动长度不变⑵拉角法：四角凹进去的类型⑶标向法：复杂图形【例1】如果在学校围墙外每隔630棵，问学校围墙的周长多少米？棵，问学校围墙的周长多少米【例2】一个楼梯的侧部剖面图，已知每步台阶宽分米，高多少米？【例3】有图为一个楼梯的侧剖面图，要在楼梯上铺红地毯。

已知红地毯每米铺地毯买红地毯需要多少钱？3米【例4】一块菜地，形状如图所示，已知c＝12米，这块地的周长是多少？米，这块地的周长是多少【例5】长方形的长是正方形后，余下一个长方形，这个长方方形后，余下形的周长是多少厘米？【例6】两个大小相同的正方形拼成了一个长方形，长方形的周长方形的周长比原来的两个正方形周长的和减少了6厘米，原来一个正方形的周长是多少厘米？答案1．答案：630×2＝1260米。

2．答案：通过平移，周长＝(3×5＋2×5)×2＝50(分米)3．答案：这道题关键在于求楼梯的长度。

经过平移，原图就转化为一个长方形，所以楼梯的长等于(3＋2)×2÷2＝5(米)，红地毯每米80元，5米应是80×5＝400(元)。

求楼梯(红地毯)的长度也可直接用3＋2＝5(米)而不必套用长方形周长公式4．答案：通过平移，周长＝(a＋b)×2＋c×2＝144 (米)5．答案：截去的最大的正方形边长等于长方形的宽，余下的长方形的周长＝50×2＝100(厘米)6．答案：把两个正方形拼成一个长方形时，拼成的长方形的周长比原来两个正方形的8条边长减少了2条边长(如图所示) 而这两条边长的和正好是减少的6厘米，所以，正方形的边长是6÷2＝3(厘米)，原来一个正方形的周长是3×4＝12(厘米)。

巧求周长一、复习(1)正方形周长：边长x 4(2)长方形周长：(长+宽)X 2二、知识讲解考点1 ：平移变做已知把若干段不知道长度的线段通过平移变成知道长度的线段，化未知为已知。

考点2:分割变大周长将一个大长方形或正方形分割成若干个长方形和正方形，那么图形周长就会增加几个长或宽考点3:拼凑变小周长将若干个小长方形或正方形拼凑成一个大长方形或正方形，图形周长就会减少几个长或宽。

三、例题讲解例1 :下图是一个楼梯的侧面图，求此图形的周长。

例2 : 下面图形是一个正方形和一个长方形组合在一起，求这个图形的周长。

例5:下图是由6个边长为2厘米的正方形组成，求此图形的周长。

例3 : 下图是由6个边长2厘米的正方形拼成的。

这个图形的周长是多少厘米?例4 :两个大小相同的正方形拼成一个长方形后，周长比原来两个正方形周长的和减少了6厘米。

原来一个正方形的周长是多少厘米？四、课堂运用1. 如下图所示，小明和小玲同时从学校到少儿书店，小明沿走，如A路线行走，小玲沿B路线行果两人速度一样，谁先到少儿书店？为什么？A110 米---------—_______________ 乂少儿书店200米3. 下面图形是两个长方形组合在一起，求这个大图形的周长。

4. 下图是由5个边长为3厘米的正方形组成的图形，求此图形的周长。

5. 从一个边长是10厘米的正方形的一角剪去一边长是4厘米的小正方形，求剩下图形的周长。

20207. 把一个正方形剪成两个大小相同的长方形后，两个长方形周长的和比原来正方形周长增 加28分米，原来正方形的周长是多少分米？课后练习题1. 如图所示，一个大长方形被三条线段分成了四个小长方形，各条线段长度见图 厘米）•求：图中四个小长方形的周长之和.厘米，原来一个正方形的周长是多少厘米？ （单位:2. 下图是由边长为1厘米的11个正方形堆成的“土”字图形•试求出其周长.3. 下图表示一块地，四周都用篱笆围起来，转弯处都是直角•已知西边篱笆长17米，南边篱笆长23米.四周篱笆长多少米?4. 求下图的周长.5.用9个相同的小长方形，组成一个大长方形，其中小长方形的长为25厘米，求这个大长方形的周长.6.（希望杯试题）右图中的阴影部分BCGF是正方形，线段FH长18厘米，线段AC长24 厘米，则长方形ADHE的周长是厘米.7.图⑴、图⑵都是由完全相同的正方形拼成的，并且图⑴的周长是周长是多少厘米？22厘米，那么图⑵的。

13．3780
【解析】
平移法转化为长方形再求．［(120＋130+60)＋(70+250)］×2×3＝3780(米)．
14．B
【解析】经过平移比拟发现 比 多两小段边，得 的周长较大．
15．一样长，360米
【解析】我们区分求甲、乙的周长．甲的周长可转化为长方形周长(如图)，即为(100+50+30)×2=360(米)．再求乙的周长．乙的周长等于长方形周长加上2个30米，即为(100+50)×2+30×2=360(米)．所以它俩走的一样长．
先思索大长方形的长上各边：运用上一道标题的结论，每条边上长为4、3、1、2的线段区分被计算了4、6、6、4次．
然后再思索大长方形的宽：由于共有 个长方形，所以长度为2的宽被计算了 次．
故总周长可以用下式计算失掉： ．
3．56
【解析】 ．
4．72
【解析】从总体思索，在求这 个小长方形的周长之和时， 、 、 、 这四条边被用了 次，其他四条虚线被用了 次，所以 个小长方形的周长之和是： 〔厘米〕。
18．以下图是一面砖墙的平面图，每块砖长20厘米，高8厘米，像图中那样一层、二层…一共摆十层，求摆好后这十层砖墙的周长是多少？
19．右图是由 个异样大小的正方形组成的，假设这个图形的面积是 平方厘米，那么它的周长是多少厘米？
20．以下图是由边长为1厘米的11个正方形堆成的〝土〞字图形．试求出其周长．
5．80
【解析】由于这块地的东边和北边的篱笆转弯处是直角，可以将东西方向的篱笆平移到最外边失掉线段 ，将南南方向的篱笆平移到最外边失掉线段 ，那么折线 的长等于折线 的长．
所以东边和北边篱笆的长区分和西边、南边的篱笆长相等．

小学奥数几何问题之巧求周长的练习题及答案
有红、黄、绿三块大小一样的正方形纸片，放在一个正方形盒内，它们之间相互叠合(如右图)，已知露在外面部分中，红色面积是20，黄色面积是12，绿色面积是8，那么正方形盒的底面积是多少?
黄色纸片露出部分与绿色纸片露出部分面积不同，把黄色纸片向左移动，在这个移动过程中，黄色纸片露出部分减少的面积等于绿色纸片纸片露出部分增加的面积，它们露出的面积和不变，所以图2中黄色露出部分面积为10，绿色面积也为10。

红、黄、绿三个长方形的面积已经求出，因为长方形中对角的面积乘积相等，故有：黄×绿=红×白。

空白长方形的面积应为10×10÷20=5，纸盒的底面积为20+10+10+5=45。

解答此题的关键是让黄色正方形纸片移动，使复杂的图形变为基本图形。