下载文档原格式
一、正等轴测投影的形成正等轴测投影的投射方向S垂直于轴测投影间P，如图7-2 a所示，且确定物体空间位置的三个坐标平面与轴测投影面均倾斜，其上的三根直角坐标轴与轴测投影面的倾角均相等，物体上平行于三个坐标平面的平面图形的正等轴测投影的形状和大小的变化均相同，因此，物体的正等轴投影的立体感颇强。
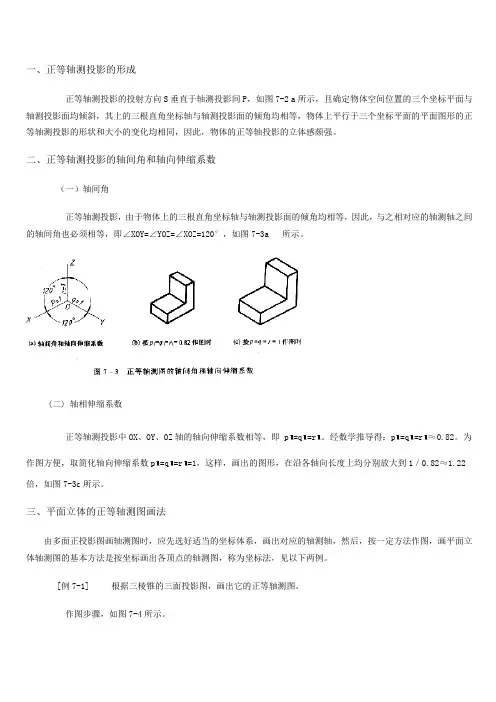
二、正等轴测投影的轴间角和轴向伸缩系数（一）轴间角正等轴测投影，由于物体上的三根直角坐标轴与轴测投影面的倾角均相等，因此，与之相对应的轴测轴之间的轴间角也必须相等，即∠XOY=∠YOZ=∠XOZ=120°，如图7-3a 所示。
(二) 轴相伸缩系数正等轴测投影中OX、OY、OZ轴的轴向伸缩系数相等，即 p=q=r。
经数学推导得：p=q=r≈0.82。
为作图方便，取简化轴向伸缩系数p=q=r=1，这样，画出的图形，在沿各轴向长度上均分别放大到1／0.82≈1.22倍，如图7-3c所示。
三、平面立体的正等轴测图画法由多面正投影图画轴测图时，应先选好适当的坐标体系，画出对应的轴测轴，然后，按一定方法作图，画平面立体轴测图的基本方法是按坐标画出各顶点的轴测图，称为坐标法，见以下两例。
[例7-1] 根据三棱锥的三面投影图，画出它的正等轴测图。
作图步骤，如图7-4所示。
[例7-2] 根据六棱柱的三面投影图，画出它的正等轴测图。
作图步骤，如图7-5所示。
本题关键在于选定坐标轴和坐标圆点，如先确定顶面各点的坐标，可避免画不必要的作图线。
四、曲面立体的正等轴测图的画法（一）坐标平面（或其平面）上的圆的正等轴测投影坐标平面（或其平行面）上圆的正等轴测投影为椭圆。
立方体平行于坐标平面的各表面上的内切圆的正等轴测投影，如图7-6所示。
从图7-6中可以看出：（1）分别平行于坐标平面的圆的正等轴测投影均为形状和大小完全相同的椭圆，但其长轴和短轴方向各不相同。
（2）各椭圆的长轴方向垂直于不属于轴测投影（即轴测轴），且在菱形（圆的外切正方形的轴测投影）的长对角线上；短轴方向平行于不属于此坐标平面的那根坐标轴的轴测投影（即轴测轴），且在菱形的短对角线上。
第三视图和正等轴测图的画法第三视角投影在欧美、日本及港台等地区的教学、设计、生产和商贸中被广泛使用。
近年来，随着与国际社会交流合作的不断深入，第三视角投影在我国的应用日渐广泛。
例如我们毕业生前往就业的外资企业（鸿准、富士康、台积电等）以及对外做出口订单的国内企业大多采用第三视角。
而我们对该方法的学习了解相对匮乏。
本文将结合范例对第三视角的投影和作图规则进行介绍及归纳总结，作为对机械制图知识的补充，以便大家查阅和更为深入的研究。
⑴认识第三视角的空间由来水平投影面H和正立投影面V将三维空间分割为如下第一组图的四部分，可以构成四组投影体系。
如图可以分辨出第三视角投影面位置。
⑵投影面及展开如果将第三视角的两个Ｈ和Ｖ平面取出，再辅助一个侧立投影平面Ｐ，那么就构成了第三角投影体系。
在这个体系中，物体位于三个平面包裹着的内部。
所以，投影平面总是在人和物体之间。
三个投影面得到投影后可以旋转到与Ｖ共面的位置。
下面是一个实例的投影三视图，观察方向分别是：下面是它的展开视图：在主视图中反应的是长和高，右视图中反应的是高和宽，俯视图中反应的是长和宽。
⑶投影规律分析第三视角三视图的仍然符合主和俯视图长对正，主和右视图高平齐，俯和右视图宽相等的“三等”投影规律。
⑷正等轴测图的画法第三视角正等轴测图的轴间角为120度，轴向变形系数都是按照1来近似绘制。
其正等轴测图符合轴测投影规律即:一、实物中与投影轴平行的轮廓线，在轴测图中仍与轴测轴平行；二、实物中相互平行的轮廓线，在轴测图中仍相互平行。
绘制过程中要按轴向1：1进行测量进行。
椭圆和圆角的画法与第一视角的画法并无区别。
总结：第三视角三视图和正等轴测图和第一视角的三视图和正等轴测图在画法操作上并没有多少本质的区别。
但是在看图方向和投影方向是不一样的。
第一视角是人（观察者）->物体->投影平面；而第三视角是人（观察者）->投影平面-> 物体。
在绘制正等轴测图中强调显示的是前视、顶视和右视三个表面。
第5章轴测图
75图5-4正等测图的轴向伸缩系数和轴间角
2．轴向伸缩系数
轴向伸缩系数p =q =r ≈0.82，为作图方便，通常采用简化的轴向伸缩系数p =q =r =1，即与轴测图平行的线段，作图时按实际长度直接量取，此时正等测图比原投影放大了1/0.82≈1.22倍。
5.2.2平面体的正等轴测图画法
画平面体轴测图有坐标法和方箱法两种，而方箱法又根据物体的形状特点，分为切割法和叠加法。
在实际作图中，多数情况下综合起来应用，因此可称为“综合法”。
1．坐标法
根据点的坐标作出点的轴测图的方法，称为坐标定点法（坐标法），它是绘制轴测图的基本方法。
画平面立体的轴测图时，首先应确定坐标原点和直角坐标轴，并画出轴测轴；然后根据各顶点的坐标，画出其轴测投影；最后依次连线，完成整个平面立体的轴测图。
【例5-1】已知三棱锥SABC 的三视图，如图5-5（a
）所示，求作正等轴测图。
图5-5三棱锥的及轴测图画法。
第三视图和正等轴测图的画法
第三视角投影在欧美、日本及港台等地区的教学、设计、生产和商贸中被广泛使用。
近年来，随着与国际社会交流合作的不断深入，第三视角投影在我国的应用日渐广泛。
例如我们毕业生前往就业的外资企业（鸿准、富士康、台积电等）以及对外做出口订单的国内企业大多采用第三视角。
而我们对该方法的学习了解相对匮乏。
本文将结合范例对第三视角的投影和作图规则进行介绍及归纳总结，作为对机械制图知识的补充，以便大家查阅和更为深入的研究。
⑴认识第三视角的空间由来水平投影面H和正立投影面V将三维空间分割为如下第一组图的四部分，可以构成四组投影体系。
如图可以分辨出第三视角投影面位置。
⑵投影面及展开如果将第三视角的两个Ｈ和Ｖ平面取出，再辅助一个侧立投影平面Ｐ，那么就构成了第三角投影体系。
在这个体系中，物体位于三个平面包裹着的内部。
所以，投影平面总是在人和物
体之间。
三个投影面得到投影后可以旋转到与Ｖ共面的位置。
下面是一个实例的投影三视图，观察方向分别是：
下面是它的展开视图：在主视图中反应的是长和高，右视图中反应的是高和宽，俯视图中反应的是长和宽。
⑶投影规律分析第三视角三视图的仍然符合主和俯视图长对正，主和右视图高平齐，俯和右视图宽相等的“三等”投影规律。
⑷正等轴测图的画法第三视角正等轴测图的轴间角为120度，轴
向变形系数都是按照1来近似绘制。
其正等轴测图符合轴测投影规律即:
一、实物中与投影轴平行的轮廓线，在轴测图中仍与轴测轴平行；
二、实物中相互平行的轮廓线，在轴测图中仍相互平行。
绘制过程中要按轴向1：1进行测量进行。
椭圆和圆角的画法与第一视角的画法并无区别。
总结：第三视角三视图和正等轴测图和第一视角的三视图和正等轴测图在画法操作上并没有多少本质的区别。
但是在看图方向和投影方向是不一样的。
第一视角是人（观察者）->物体->投影平面；而第三视角是人（观察者）->投影平面-> 物体。
在绘制正等轴测图中强调
显示的是前视、顶视和右视三个表面。
在一张正规技术交流的图纸中，为了区别视角问题往往附上图示进行提示（如下）。
其实作为技校初学者来说，首先要立足我们国家习惯使用的第一视角画法。
在学好第一视角的情况下，补充学习和练习几道简单形体的三视图和正等轴测图作业即可。
谨以此文章奉献给广大的制图爱好者，作为课堂的补充。
