下载文档原格式
用caxa软件绘制圆及相贯线的轴测图的方法黄骅市职教中心李志强轴测图的直观性在日常应用十分广泛。
尤其是教师的教学、展示，课件的制作等，更显示出它的优势。
但是，因为轴测图一般的图线不是横平竖直的，所以绘制相对复杂。
尤其是圆及相贯线的绘制，需要绘制成椭圆。
椭圆的大小方向都是我们关心的问题。
下面，我们用国产的CAXA软件绘制一下各种位置的圆及相贯线的轴测图。
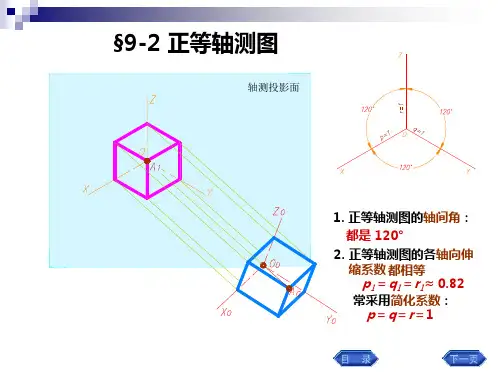
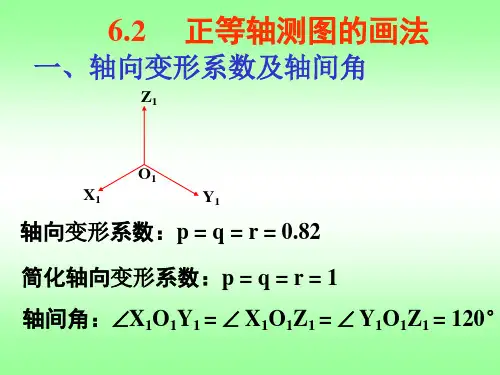
轴测图和三视图一样是物体在某一个面上的投影。
是个平面图形，为了使用方便轴测图经过了简化系数。
我们可以在轴测图的投影面上建立一个平面直角坐标系：以空间原点Ｏ的投影ｏ，作为原点。
以Ｚ轴的投影作为ｙ轴。
轴测图一般画两种，正等测图和斜二测图。
我们分别讨论图下一正等侧图。
在以上规定的坐标系下，空间X 轴的投影为平面直角坐标系中的三相限与x 轴负半轴成30度角，空间Y轴的投影为平面直角坐标系中的三相限与x轴正半轴成30度角。
空间中的任意点P空间坐标（a,b,c）。
在平面直角坐标xoy下，Py(P在Y轴的投影)坐标（√32b,−12b)，P在H面的投影Ph在xoy坐标系下坐标√3 2b−√32a,−12b−12a)，所以任意点P（a,b,c）在xoy坐标系下投影坐标为(√32(b−a),c−(a+b)/2)⁄在此基础上我们讨论三个平面上的圆的正等测图。
1 在xoy 面的圆在xoy 面（H 面）的半径为r 的圆的参数方程为{x =rcosθy =rsinθ既圆上每一点都可以表示为（rcosθ, rsinθ,0）其投影坐标为（√32(rsinθ−rcosθ),−12(rsinθ+rcosθ)) 也就是说圆的轴测图的参数方程为{x =√32(rsinθ−rcosθ)y =−12(rsinθ+rcosθ)化简为一般方程为x 2(√32r)2+2(√12r)2=1既长轴√32r 短轴√12r 的椭圆 （1） 在caxa 下 椭圆命令-----输入长轴短轴角度为0。
2 在xoz 面（v 面）的圆在xoz 面的圆参数方程为{x =rcosθy =rsinθ既圆上每一点都可以表示为（rcosθ, 0， rsinθ）其投影坐标为（−√32(rcosθ),rsinθ−12rcosθ)圆的轴测图的参数方程为{x=−√3(rcosθ)y=rsinθ−12rcosθ)在caxa中通过绘图-----公式曲线------设置参数方程实现以半径100为例参数方程设置x(t)=-86.6*cos(t)Y(t)=100*sin(t)-50*cos(t)（“()”和“* ”都不能省略）其一般方称整理锝5x2+3y2−2√3xy=r2通过化简此方程是一个椭圆方程长短轴同（1），长轴与x轴成60角。
