分析力学基础
- 格式：ppt
- 大小：2.12 MB
- 文档页数：45
下载文档原格式
合集下载
分析力学基础
牛顿的《原理》只提供了分析质点受力与运动的原型，对于复杂的力学系 统，甚至对一个简单的刚体的运动方程也还没有弄清楚。刚体的运动方程是 1765年由欧拉（Euler）最后弄清楚的。 按照当时已有的力学知识,要分析一个稍许复杂的机构,例如一个有五级 齿轮的传动系统的运动,也还是无能为力的.如果拿这个问题去请教牛顿,牛顿 只会处理自由质点运动,不会处理刚体运动,何况还是带约束的呢.而转去请教 欧拉呢?他不得不将整个系统化归为五个”隔离体”即五个刚体,分别列出五个 刚体的运动方程,而不同刚体之间又有作用力和反作用力的耦合,所以得面对 数十个方程联立的微分方程组.这样处理问题是太复杂了. 拉格朗日自有他的高招,他将这个系统简化为一个广义坐标的系统,因 为这个虽然有五个轮子的系统只要有一个参数便可以描述它的例如随便以 其中某一个轮子的转角为参数,这个参数知道了,整个齿轮系统的状态也便 知道了.然后再计算当系统动起来后系统的动能.这时便可以列出一个广义 坐标满足的二阶方程,这是何等的简便啊! 拉格朗日是怎么作到这一点的呢?
O
x
1
自由度： 2
a A
2
广义坐标： 1 2
二、受力分析：
y
b
B
F
计算广义坐标 1 、 2 对应 的 广义力
FA
FB
以下分两种方法进行计算
O
x
1
第一种方法： 解析法
xi yi zi Qk X i q Yi q Z i q i 1 k k k
即用质点系的平衡条件是： 所有的广义力都等于零
利用广义坐标表示的平衡条件求解实际问题时，关健在 于如何表达其广义力。
通常求广义力的方法有两种：
方法一：是采用公式计算
第六章 分析力学基础
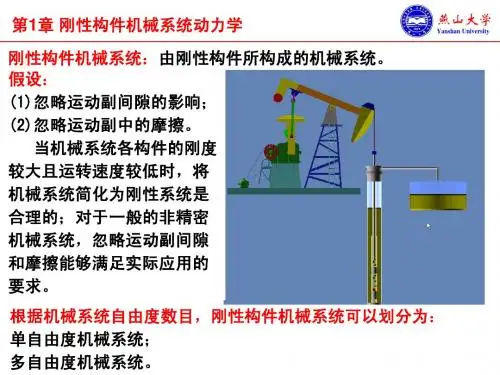
第六章 分析力学基础本章是动力学问题的引深，将介绍解决刚体和刚体系统动力学问题中经常采用的分析方法，这些方法将在某个方面使动力学问题的解决得以方便或简化，有的方法将直接涉及到动力学分析的计算机应用，这些方法包括达朗贝尔原理、虚位移原理、第一类拉格朗日方程和第二类拉格朗日方程。
第一节 达朗贝尔原理达朗贝尔原理（有的书称之为达朗伯原理）的核心是引入惯性力和惯性力矩的概念，从而将动力学问题转化为静力学问题解决。
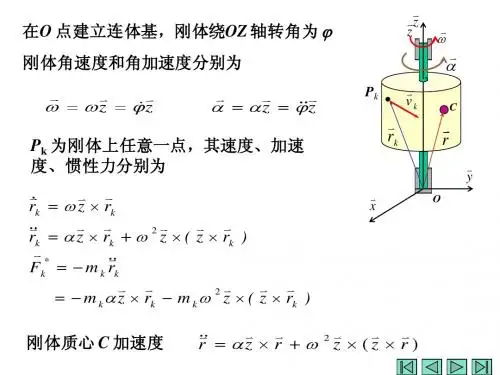
（一） 达朗贝尔惯性力我们已经知道，牛顿第二定律描述了一个质点的运动规律，即F r m = （6.1.1）这里，r表示该质点在惯性参考基中的位置，F 则表示该质点所受外力的主矢量。
如果将上式改写为0=-r m F（6.1.2）再定义r m F -=* （6.1.3）称为该质点的达朗贝尔惯性力，则牛顿第二定律可以改写为如下形式：0=+*F F （6.1.4）上式可以这样理解：质点的达朗贝尔惯性力与该质点所受到所有真实的外力的矢量和等于零，或者说，质点的达朗贝尔惯性力与该质点所受到所有真实的外力组成一个平衡力系。
这个结论称之为质点的达朗贝尔原理。
下面就（6.1.4）式作出讨论：① 所谓所有真实外力包括主动力和理想约束力。
② 达朗贝尔惯性力与非惯性基下的牵连惯性力和科氏惯性力是有区别的，后者仅仅是为了将非惯性基下的动力学方程写成类似于惯性基的形式而采用的，显然，它们取决于惯性基的运动，而达朗贝尔惯性力与非惯性基存在与否没有关系，达朗贝尔惯性力的定义为了将相对惯性基的动力学方程改写为另外一种形式，即一种力的平衡形式。
③ 达朗贝尔原理也称为动静法，即动力学问题的静力学处理方法。
④ 达朗贝尔惯性力是描述相对惯性基的运动，所以，它也直接简称为惯性力。
对于一个由n 个质点组成的质点系统，每个质点的外力中显然包含了系统内其他质点的作用力，但是对于整个系统而言，它们之间的作用力相互抵消，因此，该质点系的外力仅仅是系统外部的作用力，当然包括主动力和理想约束力。
01-1 分析力学基础
1.1 分析力学基础 1.1.1 直角坐标与广义坐标
燕山大学
Yanshan University
平面直角坐标：用平面上的长度值表示平面上一点位置的坐标。 平面直角坐标系oxy。 三维直角坐标：在二维直角坐标系（oxy）的基础上,再添加一个 垂直于x轴、y轴的坐标轴，称为z轴。x轴、y轴、z轴满足右手定 则，则坐标系oxyz为三维直角坐标。 广义坐标：能决定系统几何位置的彼此独立的量。
Q2 P L sin t cos 0
(3)系统运动微分方程
d L dt q j L Qj q j j 1, 2, , n
燕山大学
Yanshan University
Q1 P sin t 0 Q2 P L sin t cos 0
两个相互啮合的光滑表面所构成的约束
燕山大学
Yanshan University
两曲面相互啮合的约束条件：两曲面不能脱
开，也不能相互嵌入；则有： δrN1=δrN2
N1与N2两者互为作用力与反作用力：
N1= -N2 由于δrT1及δrT2与约束力N1及N2相垂直，因 而约束力在该方向不做功。在虚位移下，约 束力所做的虚功为：
x1 l1 x2 l2
特点：从运动的观点来研究系统的静力平衡问题。 优点：只考虑外力，不必考虑支反力，应用方便。
虚位移
燕山大学
Yanshan University
虚位移：约束允许的微小位移。 (1)虚位移是微小的、即时发生的，即不考虑它们发生的过程。
(2)独立的虚位移数等于系统的自由度数。
对于图示杠杆系统，杠杆两端的虚位移δx1和δx2。由于杠杆是单自 由度系统，因此δx1和δx2只有一个是独立的。
分析力学基础
n
有势力Fi在直角坐标系的投影为Fix、Fiy、Fiz
W Fix dxi Fiy dyi Fiz dzi
i 1
n
V Fix xi
V Fiy yi
n
V Fiz zi
xi yi zi 代入到广义力公式 Qk Fix Fiy Fiz q q q i 1 k k k
y
B
xB l1 sin 1 l2 sin 2 将B的坐标用广义坐标表示： yB l1 cos 1 l2 cos 2
变分
xB l1 cos 11 l2 cos 22 yB l2 sin11 l2 sin22
拉格朗日方程
§15-2 广义力与平衡条件
f k r1，r2，…，rn，t 0
设系统的一组广义坐标为
2, …, s k 1, q1，q2，……，qN N 3n s 2, …, n i 1,
将各质点的坐标表示为：
ri ri q1，q2，…，qN，t
ri ri qk k 1 qk
拉格朗日方程
§15-1 自由度和广义坐标
自由度 确定系统位置的独立参数数目
设n个质点组成的质点系，若受s个完整约束作用，
则质点系在空间的位置可以由N=3n-s个独立参数
完全确定 广义坐标
完全确定系统位置的最少参数
（ 可以是长度，角度，面积等）
对于完整系统，广义坐标数等于系统自由度数
拉格朗日方程
假设系统受s个完整约束，约束方程：
r 两边对 qk 求偏导： i qk qk
N ri ri ri qj t qk j 1 q j
有势力Fi在直角坐标系的投影为Fix、Fiy、Fiz
W Fix dxi Fiy dyi Fiz dzi
i 1
n
V Fix xi
V Fiy yi
n
V Fiz zi
xi yi zi 代入到广义力公式 Qk Fix Fiy Fiz q q q i 1 k k k
y
B
xB l1 sin 1 l2 sin 2 将B的坐标用广义坐标表示： yB l1 cos 1 l2 cos 2
变分
xB l1 cos 11 l2 cos 22 yB l2 sin11 l2 sin22
拉格朗日方程
§15-2 广义力与平衡条件
f k r1，r2，…，rn，t 0
设系统的一组广义坐标为
2, …, s k 1, q1，q2，……，qN N 3n s 2, …, n i 1,
将各质点的坐标表示为：
ri ri q1，q2，…，qN，t
ri ri qk k 1 qk
拉格朗日方程
§15-1 自由度和广义坐标
自由度 确定系统位置的独立参数数目
设n个质点组成的质点系，若受s个完整约束作用，
则质点系在空间的位置可以由N=3n-s个独立参数
完全确定 广义坐标
完全确定系统位置的最少参数
（ 可以是长度，角度，面积等）
对于完整系统，广义坐标数等于系统自由度数
拉格朗日方程
假设系统受s个完整约束，约束方程：
r 两边对 qk 求偏导： i qk qk
N ri ri ri qj t qk j 1 q j
分析力学基础
n k n k
( e)
ri 则 ( Fi mi ai )dri Q jdq j mi ai ( dq j ) i 1 j 1 i 1 j 1q j dvi ri (Q j mi )dq j 0 dt q j j 1 i 1
k n
dvi ri Q j mi 0 dt q j i 1
(i 1,2,, n)
用广义坐标表示虚位移： N ri δ ri δ qk (i 1,2,, n) k 1 qk
广义虚位移
6
§3-2 以广义坐标表示的 质点系平衡条件
7
虚功方程
ri δ ri δ qk k 1 qk
N
(i 1,2,, n)
δ W Q1 δ q1
2. 解析法
Qk ( Fxi
i 1 n
Q1
δW δ q1
9
xi yi zi Fyi Fzi ) qk qk qk
例题 1
杆 OA 和 AB 以铰链连接， O端悬挂于圆柱铰链上，如 图所示。杆长OA=a，AB=b, 杆重和铰链的摩擦都忽略 不计。今在点 A 和 B 分别作 用向下的铅垂力 FA 和 FB ， 又在点 B 作用一水平力 F 。 试求 平衡 时 1 ， 2 与 FA ， FB ，F之间的关系。
10
例 题 1
解： 杆 OA和 AB的位置可由点 A和 B的四个坐标
xA ，yA和xB ，yB完全确定，由于OA和AB杆的长 度一定，可列出两个约束方程
2 2 xA yA a2
O
x
( xB x A ) 2 ( y B y A ) 2 b2
因此系统有两个自由度。现选择1和2为系统的 两个广义坐标，计算其对应的广义力Q1和Q2。
( e)
ri 则 ( Fi mi ai )dri Q jdq j mi ai ( dq j ) i 1 j 1 i 1 j 1q j dvi ri (Q j mi )dq j 0 dt q j j 1 i 1
k n
dvi ri Q j mi 0 dt q j i 1
(i 1,2,, n)
用广义坐标表示虚位移： N ri δ ri δ qk (i 1,2,, n) k 1 qk
广义虚位移
6
§3-2 以广义坐标表示的 质点系平衡条件
7
虚功方程
ri δ ri δ qk k 1 qk
N
(i 1,2,, n)
δ W Q1 δ q1
2. 解析法
Qk ( Fxi
i 1 n
Q1
δW δ q1
9
xi yi zi Fyi Fzi ) qk qk qk
例题 1
杆 OA 和 AB 以铰链连接， O端悬挂于圆柱铰链上，如 图所示。杆长OA=a，AB=b, 杆重和铰链的摩擦都忽略 不计。今在点 A 和 B 分别作 用向下的铅垂力 FA 和 FB ， 又在点 B 作用一水平力 F 。 试求 平衡 时 1 ， 2 与 FA ， FB ，F之间的关系。
10
例 题 1
解： 杆 OA和 AB的位置可由点 A和 B的四个坐标
xA ，yA和xB ，yB完全确定，由于OA和AB杆的长 度一定，可列出两个约束方程
2 2 xA yA a2
O
x
( xB x A ) 2 ( y B y A ) 2 b2
因此系统有两个自由度。现选择1和2为系统的 两个广义坐标，计算其对应的广义力Q1和Q2。
[物理]分析力学基础
![[物理]分析力学基础](https://img.taocdn.com/s1/m/cff17a52f46527d3240ce040.png)
令
xi yi zi Qk ( Fxi Fyi Fzi ) (k 1,, N ) qk qk qk i 1
n
则有 WF Qkqk 0
k 1
N
与广义坐标qk对 应的广义力，量 纲可为力或力矩。
虚功方程（用广义力广义坐标表示）
WF Qk qk 0
于是，虚位移原理的表达式成为
V 0
上式说明，在势力场中，具有理想约束的质点系的平 衡条件为质点系的势能在平衡位置处一阶变分为零。 如果用广义坐标 q1，q2， ，qN 表示质点系的位置, 则质点系的势能可以写成广义坐标的函数，即
V V q1，q2， ，qN
根据广义力表达式，在势力场中可将广义力 QN 写成 用势能表达的形式，即
述了质点系的几何约束方程。
xi xi q1 , q2 ,, q N , t yi yi q1 , q2 ,, q N , t i 1,2,, n zi zi q1 , q2 , , q N , t
一旦确定了质点系的广义坐标，则也隐含地描
z
M
y
z
j
R
M
y
x
z R (x y )
2 2 2
x
q
若质点 M 限定在半球面上运动，球半径为R。是 具有1个质点的空间质点系，有1个约束方程：
n 1, s 1
自由度数为：
N 3n s 3 1 2
通常用 2 个独立参数 j 和 q 表示。
z
j
R
M
y
x
q
质点 M 的空间坐标可用广义坐标表示为：
3、用广义坐标表示虚位移——广义虚位移
ri ri q1 , q2 ,, qN , t i 1,2, ,n
[物理]分析力学基础
xi yi zi Qk ( Fxi Fyi Fzi ) qk qk qk V xi V yi V zi ( ) xi qk yi qk zi qk V qk (k 1， 2， ，N )
这样，由广义坐标表示的平衡条件可写成如下形式
ri ri qk k 1 qk
N
或
二、以广义坐标表示的质点系平衡条件
在虚位移原理中，以质点直角坐标的变分表示 虚位移。这些虚位移通常不独立，需要建立虚位移 之间的关系。若直接用广义坐标变分来表示虚位移， 广义虚位移之间相互独立，虚位移原理可表示为简 洁形式。为此将广义虚位移代入虚功方程
x R sin j cosq y R sin j sin q Z R cosq
一般地，设有由 n 个质点组成的非自由质点系的
位置可由 N 个广义坐标
q1 , q2 ,, qN来确定，则
质点系内各质点的坐标可表为广义坐标的函数，即
或写为：ri ri q1 , q2 ,, q N , t
z
M
yห้องสมุดไป่ตู้
z
j
R
M
y
x
z R (x y )
2 2 2
x
q
若质点 M 限定在半球面上运动，球半径为R。是 具有1个质点的空间质点系，有1个约束方程：
n 1, s 1
自由度数为：
N 3n s 3 1 2
通常用 2 个独立参数 j 和 q 表示。
z
j
R
M
y
x
q
质点 M 的空间坐标可用广义坐标表示为：
3、用广义坐标表示虚位移——广义虚位移
ri ri q1 , q2 ,, qN , t i 1,2, ,n
分析力学基础
p mi ri ri i 1 qk ql
qk ql
第5章 分析力学基础
或：
5.3 动能和势能
1 n n V ＝ mk l qk ql 2 k 1 l 1 p k 和 ql 为广义速度， mk l 为广义质量系数， k l ＝ mi ri ri 。 m 其中，q qk ql i 1
虚位移原理的另一种表述
若系统有n个自由度，任意一点的坐标矢量可以用n个广义坐标和时间 t来表示，即：r ＝r ( q ， ， ， ， ) q q t
i i 1 2 n
由于虚位移与时间无关，则有：
代入虚功方程，得：
p n
ri d ri ＝ d qk k 1 q k
n
ri d W ＝ Fi d qk i 1 k 1 q k
第5章 分析力学基础
对换求和的次序，得：
5.2 虚位移原理
p ri d W ＝ Fi i 1 q k 1 k p ri 其中， Qk ＝ Fi q i 1 k 义力。
n
d qk
(k 1, 2, , n) 为与广义坐标qk 对应的广
势力场和势力
质点从力场中某一位置运动到另一位置时，作用力的功与质点经历的路 径无关，而只与其起点及终点位置有关，这就是所谓的势力场。重力场、 万有引力场和弹性力场都是势力场。在势力场中质点所受的力称为势力。
势能
所谓势能是把质点从当前位置移至势能零点的过程中势力所作的功。根据势 能的定义，特别需要强调的是：势能大小与规定的势能零点位置有关。
这样，虚功方程可以写成：
d W ＝ Q d q ＝ 0
n k k k 1
第一章 分析力学基础
唯一的数y与之对应，则称在集合E上给定了一个函数
y = f (x) (x, y R)
在闭区间a, b上的连续函数A（x），积分
b
I = a A(x)dx
设定义在 a, b上的所有连续函数组成的集合为 ，则
上式给出了集合 到数域R的一个映射关系，称之为泛函 数，记为
I (A) (I R,A )
n个质点组成的质点系，任一瞬时这n个质点在空间中 位置的集合称为该质点系的位形。
所有满足约束条件的质点系的位形的集合称为该质点 系位形空间 。可以证明，对于完整约束系统，位形空间为 线性空间。
对于保守系统，位形空间的每一个元素（即质点系的 每一个位形），都有唯一的势能值与之对应，因此，质点 系的势能可以看成是定义在位形空间的一个泛函数。
n
δWF δWFi i 1
n
i 1
( Fix
N k 1
xi qk
δqk
Fiy
N k 1
yi qk
δqk
Fiz
N k 1
zi qk
δqk )
N n (Fix
k 1 i1
xi qk
Fiy
yi qk
Fiz
zi qk
)δqk 0 Nhomakorabea令Qk
n
( Fix
i 1
xi qk
Fiy
yi qk
势能变分的定义
设y=f（x）是定义在数域R上的可微函数，当自变量x发生 微小变化dx时，对应函数值的微小变化称为函数的微分，记 作
dy = f (x + dx) - f (x) = f (x)dx
设 I (A) 是定义在集合 上的泛函数，当自变量A发 生微小变化 A 时，对应泛函数值的微小变化称为泛函数的 变分
y = f (x) (x, y R)
在闭区间a, b上的连续函数A（x），积分
b
I = a A(x)dx
设定义在 a, b上的所有连续函数组成的集合为 ，则
上式给出了集合 到数域R的一个映射关系，称之为泛函 数，记为
I (A) (I R,A )
n个质点组成的质点系，任一瞬时这n个质点在空间中 位置的集合称为该质点系的位形。
所有满足约束条件的质点系的位形的集合称为该质点 系位形空间 。可以证明，对于完整约束系统，位形空间为 线性空间。
对于保守系统，位形空间的每一个元素（即质点系的 每一个位形），都有唯一的势能值与之对应，因此，质点 系的势能可以看成是定义在位形空间的一个泛函数。
n
δWF δWFi i 1
n
i 1
( Fix
N k 1
xi qk
δqk
Fiy
N k 1
yi qk
δqk
Fiz
N k 1
zi qk
δqk )
N n (Fix
k 1 i1
xi qk
Fiy
yi qk
Fiz
zi qk
)δqk 0 Nhomakorabea令Qk
n
( Fix
i 1
xi qk
Fiy
yi qk
势能变分的定义
设y=f（x）是定义在数域R上的可微函数，当自变量x发生 微小变化dx时，对应函数值的微小变化称为函数的微分，记 作
dy = f (x + dx) - f (x) = f (x)dx
设 I (A) 是定义在集合 上的泛函数，当自变量A发 生微小变化 A 时，对应泛函数值的微小变化称为泛函数的 变分
分析力学基础
r =(e 0 0)
T
由结构对称性，可知OZ 轴为圆盘的惯性主轴 由结构对称性，可知 利用惯性力和惯性力矩公式，可得 利用惯性力和惯性力矩公式，
αy + ω 2 x ω 2 me * 2 F = m − αx + ω y = 0 0 0
yA = r v A − ωr = 0
定常约束与非定常约束 约束方程中不显含时间的约束称为定常约束（ 约束方程中不显含时间的约束称为定常约束（稳定 定常约束 约束） 否则称为非定常约束 不稳定约束） 非定常约束（ 约束），否则称为非定常约束（不稳定约束）。 完整约束与非完整约束 约束方程中的变量只是坐标和时间而不包含坐标对 时间的导数，或者微分项（坐标对时间的导数） 时间的导数，或者微分项（坐标对时间的导数）可 以积分为有限形式，这类约束称为完整约束 完整约束。 以积分为有限形式，这类约束称为完整约束。 约束方程中包含坐标对时间的导数， 约束方程中包含坐标对时间的导数，而且方程不能 积分为有限形式，这类约束称为非完整约束 非完整约束。 积分为有限形式，这类约束称为非完整约束。 约束方程不包含时间 以及质点速度，这类约束称为稳 定的完整约束 。
点建立连体基，刚体绕OZ 轴转角为 ϕ 在O 点建立连体基，刚体绕 刚体角速度和角加速度分别为
z z
ω
α
Pk
ɺ ω = ωz = ϕz
ɺ α = α z = ϕɺz
vk
C
Pk 为刚体上任意一点，其速度、加速 为刚体上任意一点，其速度、 度、惯性力分别为
rk
O
r
y
ɺ rk = ω z × rk ɺɺ = α z × r + ω 2 z × ( z × r ) rk k k F * = − m ɺɺ r
分析力学基础
分析力学（第六章）零． 总说矢量力学侧重于几何和矢量的应用； 分析力学偏重于解析数学；两者风格不同，但在力学范围内完全等价，由于分析力学具有普适的表述方式，可推广到其它学科中应用。
一．分析力学的基本概念1．系统描述相关的概念（1）力学系：n 个相互作用着的质点构成的力学系统； （2）位形：力学系的位置状态； （3）约束：限制质点自由运动的条件；分类：几何约束（限制几何位置），微分约束（约束中包含速度）不完整约束稳定约束（与时间无关），不稳定约束（与时间有关） 可解约束（可以解除），不可解约束（不可以解除） （4）自由度s ：描写力学系所须独立坐标的个数 k n s -=3 约束方程的个数 自由度数目 质点的个数（5）广义坐标：s 个独立坐标参量可以把体系3n 个坐标参量表示出来：)3,,2,1(),;,,,(21n i t q q q x xs i i==。
s 个独立坐标参量称为广义坐标（6）广义速度：广义速度分量),,2,1(,s dtdq q==ααα的全体2．系统原理相关的概念（1） 实位移：在时间间隔（0≠dt）内发生的真实位移r d（2） 虚位移：设想发生的位移rδ（时间没变化，非真正的位移） 在稳定约束下，实位移是虚位移中的一个；在不稳定约束下，实位移不同于虚位移（P167,图6.2）；（3） 虚功：力在虚位移下所作的功（4） 理想约束：体系中约束力所作的功之和为零 01=⋅∑=r F ni N iδ光滑曲面、曲线、铰链；不可伸长的杆、绳；固定点约束； 固定曲面上的纯滚动等都是理想约束。
（5） 拉格朗日函数（拉氏函数或拉格朗日量）体系的动能和势能之差);();,();,(t q V t q q T t qq L -= 适用于体系受保守力的情况。
（6） 广义动量：αααqT qL p∂∂=∂∂=αq 为线量时，αp 为动量分量；αq 为角量时，αp 为角动量分量；（7） 广义力：αααq x F q W t q q q Qi ni is ∂∂=∂∂=∑=3121);,,,( 的全体αq 为线量时，αQ 为力的分量；αq 为角量时，αQ 为力矩分量；（8） 哈密顿函数（或哈密顿量）αααqp L t p q H s∑=+-=1);,(应把广义速度都看成p q ,的函数（9） 正则变量：广义坐标和广义动量称为力学系的正则变量； ),,2,1(,s q p=ααα构成2s 维抽象空间，任一瞬时力学系的广义坐标和广义动量确定了相空间的一个点（称为相点）（10）泊松括号：∑=∂∂∂∂-∂∂∂∂=sq H p G p H q G H G 1)(],[ααααα体系的某一力学量，哈密顿量二．基本原理1． 虚功原理质点i 处于平衡状态：),,2,1( 0s i r F r F W i N i i ii==⋅+⋅=δδδ体系处于平衡状态：011=⋅+⋅=∑∑==ni i N ni i i r F r F W iδδδ（1）坐标表示在理想约束的情况下，力系的平衡条件是作用在质点上的主动力所作的虚功之和等于零：∑=⋅=ni iix FW 31δδ（2）广义坐标表示 )3,,2,1( 11n i q q x t tx q q x xsi i si i=∂∂=∂∂+∂∂=∑∑==ααααααδδδδαααααααααδδδδq Qq q x Fq q x F Wssni iis i ni i∑∑∑∑∑======∂∂=∂∂=1131131)(广义力分量 体系处于平衡时，广义力分量都应等于零。
第17章 分析力学基础
W1
2
B
W2
P
即 ( P cos1 (0.5W1 W2 ) sin 1 )l11 ( P cos2 0.5W2 sin 2 )l2 2 0 ∵ 1 、 2彼此独立， ∴上式中1、2前的系数须分别为零， P cos1 (0.5W1 W2 ) sin 1 0 即 P cos2 0.5W2 sin 2 0 解得
§4 拉格朗日方程
将动力学普遍方程用独立的广义 坐标表示，即可推导出
第二类拉格朗日方程。
拉格朗日
拉格朗日 （Lagrange 1736 — 1813）法 籍意大利人，数学 家、力学家、天文 学家，十九岁成为 数学教授，与。
x
W2
B
( P cos 2 0.5W2 sin 2 )l2 2 0
P cos 2 0.5W2 sin 2 0
解得
2P 2 arctan W 2
§3 动力学普遍方程
引言
K •摆长不定，如何 确定其摆动规律？
φ1 φ2 •多杆摆问题
1 rC1 C1
y
rA rC2
W1 A
x
W
2 C2
rB
B
P
F
P rB W1 rC1 W2 rC 2 0
W2
Pl11 cos1 W1 0.5l1 sin 1 W2l11 sin 1 0
( P cos1 (0.5W1 W2 ) sin1 )l1 1 0 P cos1 (0.5W1 W2 ) sin1 0
即
在理想约束条件下，质点系的各个质点在任意瞬 时所受的主动力和虚加的惯性力在任一虚位移上 所做虚功之和等于零。
分析力学竞赛知识点总结
分析力学竞赛知识点总结一、基本概念1. 相互作用力：相互作用力是物体之间产生的相互作用力，包括接触力、重力、弹力等。
在分析力学中，需要根据物体的运动状态来分析相互作用力的大小和方向。
2. 牛顿定律：牛顿定律是分析力学的基础，包括牛顿第一定律、牛顿第二定律和牛顿第三定律。
竞赛选手需要熟练掌握这些定律，能够灵活运用到解题中。
3. 动量和动量定理：动量是描述物体运动状态的物理量，动量定理是描述物体受力变化时动量的变化规律。
在竞赛中，需要掌握动量和动量定理的计算方法，能够准确地应用到实际问题中。
4. 力的合成：力的合成是指多个力合成一个力的过程，竞赛选手需要熟练掌握力的合成的方法，能够准确地求解合成后的力的大小和方向。
5. 动力学方程：动力学方程是描述物体运动规律的基本方程，包括牛顿第二定律、角动量定理等。
在竞赛中，需要熟练掌握动力学方程的推导和应用，能够灵活运用到解题中。
二、公式推导1. 牛顿第二定律的推导：牛顿第二定律是分析力学的基本定律，竞赛选手需要熟练掌握牛顿第二定律的推导过程，能够准确地应用到解题中。
2. 动量定理的推导：动量定理是描述物体受力变化时动量的变化规律，竞赛选手需要熟练掌握动量定理的推导过程，能够准确地应用到解题中。
3. 力的合成公式的推导：力的合成是分析力学中的重要内容，竞赛选手需要熟练掌握力的合成公式的推导过程，能够准确地求解合成后的力的大小和方向。
4. 动力学方程的推导：动力学方程是描述物体运动规律的基本方程，竞赛选手需要熟练掌握动力学方程的推导过程，能够灵活运用到解题中。
三、解题技巧1. 熟练掌握基本概念：竞赛选手需要熟练掌握分析力学的基本概念，包括相互作用力、牛顿定律、动量和动量定理、力的合成、动力学方程等，能够准确地应用到解题中。
2. 灵活运用公式：竞赛选手需要灵活运用公式，能够根据题目要求准确地选择合适的公式进行计算，并且能够准确地推导公式，解决复杂问题。
3. 掌握解题方法：竞赛选手需要掌握解题的方法，能够根据题目的特点合理地选择解题的方法，在有限的时间内快速准确地解答问题。
分析力学基础
理论力学 ( II )
第 三 章 分析力学基础
自由度和广义坐标是分析力学最基本的概念. 自由度和广义坐标是分析力学最基本的概念. 虚位移原理的广义坐标描述便是: 虚位移原理的广义坐标描述便是: 对应于各广 义坐标的广义力分别为零是系统静止平衡的充 要条件. 虚位移原理也称静力学普遍方程. 要条件. 虚位移原理也称静力学普遍方程.虚位 移原理与达朗伯原理的结合便得到动力学普遍 方程. 方程. 动力学普遍方程的广义坐标表达可得到 拉格朗日方程. 拉格朗日方程. 确切地说是第二类拉格朗日方 程.它是完整约束下的质点系统的运动微分方 程通式.
k =1 k =1
N
的广义力. 称Qk 为系统对应于广义坐标qk 的广义力 ( k = 1、2、3……N ) 、 、 广义力的求法: 广义力的求法 (1) 在直角坐标系下
∂x i ∂y i ∂z i Qk = ∑ ( Fix ) + Fiy + Fiz ∂q k ∂q k ∂q k i =1
n
( k = 1 , 2 , 3.......N )
x D = b cos α + l cos β δx D = − b sin αδα − l sin βδβ δy D = a cos αδα + l cos βδβ
D
F
x y = a sin α + l sin β C
由
∑ (F
ix
⋅ δ x i + F iy ⋅ δ y i ) = 0
F δ x D + Py C = 0
N
用直角坐标系下的投影表达为: 用直角坐标系下的投影表达为
xi = x i ( q1 ,q2 ,q3 ......q N ) yi = yi ( q1 ,q2 ,q3 ......q N ) z i = z i ( q1 ,q2 ,q3 ......q N ) δx i = ∑ ∂x i ⋅ δqk ∂qk k =1 N ∂y δy i = ∑ i ⋅ δq k k = 1 ∂q k N ∂z δz i = ∑ i ⋅ δqk k = 1 ∂q k
第 三 章 分析力学基础
自由度和广义坐标是分析力学最基本的概念. 自由度和广义坐标是分析力学最基本的概念. 虚位移原理的广义坐标描述便是: 虚位移原理的广义坐标描述便是: 对应于各广 义坐标的广义力分别为零是系统静止平衡的充 要条件. 虚位移原理也称静力学普遍方程. 要条件. 虚位移原理也称静力学普遍方程.虚位 移原理与达朗伯原理的结合便得到动力学普遍 方程. 方程. 动力学普遍方程的广义坐标表达可得到 拉格朗日方程. 拉格朗日方程. 确切地说是第二类拉格朗日方 程.它是完整约束下的质点系统的运动微分方 程通式.
k =1 k =1
N
的广义力. 称Qk 为系统对应于广义坐标qk 的广义力 ( k = 1、2、3……N ) 、 、 广义力的求法: 广义力的求法 (1) 在直角坐标系下
∂x i ∂y i ∂z i Qk = ∑ ( Fix ) + Fiy + Fiz ∂q k ∂q k ∂q k i =1
n
( k = 1 , 2 , 3.......N )
x D = b cos α + l cos β δx D = − b sin αδα − l sin βδβ δy D = a cos αδα + l cos βδβ
D
F
x y = a sin α + l sin β C
由
∑ (F
ix
⋅ δ x i + F iy ⋅ δ y i ) = 0
F δ x D + Py C = 0
N
用直角坐标系下的投影表达为: 用直角坐标系下的投影表达为
xi = x i ( q1 ,q2 ,q3 ......q N ) yi = yi ( q1 ,q2 ,q3 ......q N ) z i = z i ( q1 ,q2 ,q3 ......q N ) δx i = ∑ ∂x i ⋅ δqk ∂qk k =1 N ∂y δy i = ∑ i ⋅ δq k k = 1 ∂q k N ∂z δz i = ∑ i ⋅ δqk k = 1 ∂q k
分析力学基础
l2
B
l 2 1
2
F2
F
F2 l 2 sin 2 Fl2 cos 2 Q1 ( F1 F2 )l1 sin 1 Fl1 cos1 0 Q2 F2 l2 sin 2 Fl2 cos 2 0
tg1
×
F tg 2 F2
×
xi xi (q1 , q2 ,, qN ) yi yi (q1 , q2 ,, qN ) zi zi (q1 , q2 ,, qN )
ri xi i yi j zi k ri xi i yi j zi k
N xi xi xi xi xi q1 q2 q N qk q1 q2 q N k 1 q k
1 l1
y
A
2 F1
l2
B
F tg1 F1 F2
F2
F
×
方法 2：
x
2 不变，给 1 虚位移 1
y A l1 sin 1 1
x B l1 cos1 1 y B l1 sin 1 1
y
1 l1
1
l1 1
A
W1 F1y A F2y B Fx B Q1 1 1
n WF Firi (Fixxi Fiyyi Fizzi )
n i 1 i 1
xi xi q k k 1 q k
N
xi yi zi ( Fix qk Fiy qk Fiz qk ) i 1 k 1 q k k 1 q k k 1 q k
×
F1l1 sin 1 F2 l1 sin 1 Fl1 cos1 0 F1l 2 sin 2 F2 l 2 sin 2 Fl2 cos 2 0
B
l 2 1
2
F2
F
F2 l 2 sin 2 Fl2 cos 2 Q1 ( F1 F2 )l1 sin 1 Fl1 cos1 0 Q2 F2 l2 sin 2 Fl2 cos 2 0
tg1
×
F tg 2 F2
×
xi xi (q1 , q2 ,, qN ) yi yi (q1 , q2 ,, qN ) zi zi (q1 , q2 ,, qN )
ri xi i yi j zi k ri xi i yi j zi k
N xi xi xi xi xi q1 q2 q N qk q1 q2 q N k 1 q k
1 l1
y
A
2 F1
l2
B
F tg1 F1 F2
F2
F
×
方法 2：
x
2 不变，给 1 虚位移 1
y A l1 sin 1 1
x B l1 cos1 1 y B l1 sin 1 1
y
1 l1
1
l1 1
A
W1 F1y A F2y B Fx B Q1 1 1
n WF Firi (Fixxi Fiyyi Fizzi )
n i 1 i 1
xi xi q k k 1 q k
N
xi yi zi ( Fix qk Fiy qk Fiz qk ) i 1 k 1 q k k 1 q k k 1 q k
×
F1l1 sin 1 F2 l1 sin 1 Fl1 cos1 0 F1l 2 sin 2 F2 l 2 sin 2 Fl2 cos 2 0
《分析力学基础》课件
容
哈密顿-雅可比 方程可以描述 系统的运动状 态和能量变化
哈密顿-雅可比 方程在分析力 学中具有重要
地位
正则方程的定义和性 质
正则方程的求解方法
正则方程在分析力学 中的应用
正则方程与拉格朗日 方程的关系
正则方程在工程中的 应用实例
课件结构
● 引言：介绍分析力学的基本概念和重要性 ● 第一部分：牛顿力学 ● 牛顿三定律 ● 动量守恒定律 ● 角动量守恒定律 第二部分：拉格朗日力学
弹性模量：描述固体材料弹 性性质的物理量
胡克定律：描述固体材料在弹 性范围内的应力与应变关系
泊松比：描述固体材料在弹性 范围内的横向应变与纵向应变
的关系
弹性力学基本方程：描述固体 材料在弹性范围内的应力、应
变和位移之间的关系
哈密顿原理：描述系统演化的普遍 规律，适用于经典力学和量子力学
哈密顿原理的应用：求解力学问题， 如求解运动方程、求解哈密顿量等
分析力学基础PPT课 件大纲
汇报人：
目录
添加目录标题
课件简介
课件内容
课件结构
课件效果
课件使用说明
添加章节标题研究物体在力作用下的运动规律
课件旨在帮助学生理解分析力学的基本概念、原理和方法
课件适用于物理专业学生、教师和相关研究人员
课件内容涵盖了分析力学的主要内容，包括牛顿力学、拉格朗日力学和哈密顿力 学等
页脚：包括作者、日期、版权等信息
背景：选择与主题相关的背景图片或颜 色
课件效果
课件内容：包括基 本概念、原理、公 式、应用等
教学方法：采用案 例分析、实验演示、 互动讨论等方式
学习效果：提高分 析力学知识水平， 增强解决问题的能 力
哈密顿-雅可比 方程可以描述 系统的运动状 态和能量变化
哈密顿-雅可比 方程在分析力 学中具有重要
地位
正则方程的定义和性 质
正则方程的求解方法
正则方程在分析力学 中的应用
正则方程与拉格朗日 方程的关系
正则方程在工程中的 应用实例
课件结构
● 引言：介绍分析力学的基本概念和重要性 ● 第一部分：牛顿力学 ● 牛顿三定律 ● 动量守恒定律 ● 角动量守恒定律 第二部分：拉格朗日力学
弹性模量：描述固体材料弹 性性质的物理量
胡克定律：描述固体材料在弹 性范围内的应力与应变关系
泊松比：描述固体材料在弹性 范围内的横向应变与纵向应变
的关系
弹性力学基本方程：描述固体 材料在弹性范围内的应力、应
变和位移之间的关系
哈密顿原理：描述系统演化的普遍 规律，适用于经典力学和量子力学
哈密顿原理的应用：求解力学问题， 如求解运动方程、求解哈密顿量等
分析力学基础PPT课 件大纲
汇报人：
目录
添加目录标题
课件简介
课件内容
课件结构
课件效果
课件使用说明
添加章节标题研究物体在力作用下的运动规律
课件旨在帮助学生理解分析力学的基本概念、原理和方法
课件适用于物理专业学生、教师和相关研究人员
课件内容涵盖了分析力学的主要内容，包括牛顿力学、拉格朗日力学和哈密顿力 学等
页脚：包括作者、日期、版权等信息
背景：选择与主题相关的背景图片或颜 色
课件效果
课件内容：包括基 本概念、原理、公 式、应用等
教学方法：采用案 例分析、实验演示、 互动讨论等方式
学习效果：提高分 析力学知识水平， 增强解决问题的能 力
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
计算采用动静法
在构件运动的某一时刻，将分布惯性力加在构 件上，使原来作用在构件上的外力和惯性力假 想地组成平衡力系，然后按静荷作用下的问题 来处理。
一、直线运动构件的动应力
例6-1 图示梁、钢索结构。起吊重物以等加速度a提升。试求钢索横截面的 动应力和梁的最大动应力。
解：(1) 钢索的轴力：
a
P
FNd
，试确定圆环的动应力，并建立强度条件。
qd
解：①惯性力分析:
t
O D
qd
Aan
g
AD2
2g
a
n
D
2
2
②内力分析如图
qd
FNd
FNd
图2
③应力分析
2FNdqdD0 FNdqd2DA4gD2 2
d
FNdD22
A 4g
v2
g
④强度条件
d
v 2
g
v [ ] g
最大线速度：
vmax
[ ] g
§6－3 构件受冲击时动应力计算
计算采用能量守恒定律 冲击物在冲击过程中减少的动能 Ek 和势能Ep 等 于被冲击构件所增加的应变能 Vd ，即
EkEp Vεd (a)
一、自由落体冲击问题
设重量为P的重物，从高度h自由落下，冲击到等截 面直杆AB的B端。杆AB长度为l ，横截面面积为A。
A
A
A
P
h
B (a)
Fd
Δd
B (b)
三、动荷系数：
动荷系数 Kd
动响应 静响应
d Kdst
四、动应力分类：
1.简单动应力： 加速度可以确定的，采用“动静法”求解。 2.冲击载荷： 速度在极短暂的时间内有急剧改变，此时，加 速度不能确定，要采用“能量法”求之；
3.交变应力： 应力随时间作周期性变化，疲劳问题。
§6－2 构件有加速度时动应力计算
P
Δst
B
(c)
假设：1.冲击物变形与回弹可忽略。 2.AB杆质量可忽略。 3.冲击过程的能量耗散可忽略。
则当冲击物速度降为零时，杆AB发生最大伸长d ，
则冲击物减少的势能为
Ep P(hΔd)
(b)
而冲击物的初速与终速均为零，故
Ek 0
(c)
杆内应变能
Vεd
EA 2l
Δd2
(d)
将(b)(c)(d)代入(a)得
d Kdst
(1)
当 h0 时，相当于P 骤加在杆件上，这时
Kd 2
对于实际情况，以上计算是偏于安全的。
例6-5 已知：d1=0.3m, l=6m, P=5kN, E1=10Gpa, 求两种情况的动应力。（1）H=1m自由下落；（2） H=1m, 橡皮垫d2=0.15m, h=20mm,E2=8Mpa.
分析力学基础
分析力学基础-6 动载荷，交变应力
§6－1 概 述
一、静载荷与动载荷： 载荷不随时间变化（或变化极其平稳缓慢）且使构件各部件加速度保持为零（或可 忽略不计），此类载荷为静载荷。 载荷随时间急剧变化且使构件的速度有显著变化（系统产生惯性力），此类载荷为 动载荷。
二、动响应： 构件在动载荷作用下产生的各种响应（如应力、应变、位移等），称为动响应。 实验表明：在静载荷下服从虎克定律的材料，只要应力不超过比例极限 ,在动载荷 下虎克定律仍成立且E静=E动。
dm , a xKd ma x(1g a)M W m z ax
6q st
2q st M 图（ N·m)
(c)
由工字钢的弯矩图(图c)可知，Mmax=6qstN·m ，并由 型钢表查得Wz=21.210-6 m3以及已知数据代入上式， 得
(6 2.5 0 9 .8)N 1m
dm , a x 2 .022.2 1 1 6 0 m 3 1M 15Pa
FNd
P
P g
a
0
FNd
P
P a P(1 g
a) g
P
(2)钢索横截面的动应力：
P a dF A Nd P A(1a g)s(t1a g) g
令
Kd
1
a g
称为动荷因数，则
d Kdst
梁的弯矩：
MdmaxKdMstKd4Pl
梁的最大动应力：
dmaxMW dmaxK4dW Pl
例6-2 长度 l=12m 的16号工字钢，用横截面面积为 A=108mm2 的钢索起吊，如图a所示，并以等加速度 a=10m/s2 上升。若只考虑工字钢的重量而不计吊索 自重，试求吊索的动应力，以及工字钢在危险点的动
二、转动构件的动应力:
例6-3 重为G的球装在长L的转臂端部，以等角速度
在光滑水平面上绕O点旋转， 已知许用强度[] ，求
转臂的截面面积（不计转臂自重）。
O
L
FNd
解：①受力分析如图:
惯性力：
FNdmna2Rm 2LG /g
②强度条件
F N/dA
A
FNd
2GL
(g)
例6-4 设圆环的平均直径D、厚度t ，且 t«D，环的 横截面面积为A，单位体积重量为 ，圆环绕过圆心 且垂直于圆环平面的轴以等角速度旋转，如图所示
P(hΔd)E2lAΔd2 Pl
注意 EA ，Δst即在静载P下AB杆的伸长，则上式可
简化成
Δ d 22Δ sΔ td2Δ sh t 0
解出 d 的两个根，取其中大于 st 的那个根，即得
Δd Δst(1
1 2h) Δst
引用记号
2h
Kd (1
1 ) Δst
则
Δd KdΔst
(e)
将上式两边乘以 E/l 后得
qqstqd qst(1ga)
引入动荷因数
a Kd 1 g
则 qKdqst
由对称关系可知，两吊索的轴力 （F N参见图b）相
等，其值可由平衡方程 ，Fy 0 2FNqslt 0
求得
FN
1 2
qstl
Fq
N
st
F
N
(b)
A
B
吊索的静应力为
FN qstl
A 2A
故得吊索的动应力为 d Kd(1ga)q2sAtl
P H
d1
P
解：（1）
d2
h
st
Pl E1 A1
=0.0425 mm
d1 l
2H
Kd 1
1 st
218
dKdst1.5 4M 2 Pa
(2)
由型钢表查得 qst=20.5kg/m=(20.5N/m)g及已知数 据代入上式，即得
d (1 9 1 .8 m m 0 1 2 2)/ /( s 2 s.5 2 0 9 1 .8N 0 1 1) 6 8 1 /0 (m 2 ) 2.6 M 2 Pa
同理，工字钢危险截面上危险点处的动应力
应力d,max
2m 4m 4m 2m
(a) a
A
C
B
2.484m 7.032m 2.484m
(d)
A
B
z y
解：将集度为 qd=Aa 的惯性力加在工字钢上，使工
字钢上的起吊力与其重量和惯性力假想地组成平衡力
系。若工字钢单位长度的重量记为 qst ，则惯性力集 度为
qd
qst
a g
于是，工字钢上总的均布力集度为
在构件运动的某一时刻，将分布惯性力加在构 件上，使原来作用在构件上的外力和惯性力假 想地组成平衡力系，然后按静荷作用下的问题 来处理。
一、直线运动构件的动应力
例6-1 图示梁、钢索结构。起吊重物以等加速度a提升。试求钢索横截面的 动应力和梁的最大动应力。
解：(1) 钢索的轴力：
a
P
FNd
，试确定圆环的动应力，并建立强度条件。
qd
解：①惯性力分析:
t
O D
qd
Aan
g
AD2
2g
a
n
D
2
2
②内力分析如图
qd
FNd
FNd
图2
③应力分析
2FNdqdD0 FNdqd2DA4gD2 2
d
FNdD22
A 4g
v2
g
④强度条件
d
v 2
g
v [ ] g
最大线速度：
vmax
[ ] g
§6－3 构件受冲击时动应力计算
计算采用能量守恒定律 冲击物在冲击过程中减少的动能 Ek 和势能Ep 等 于被冲击构件所增加的应变能 Vd ，即
EkEp Vεd (a)
一、自由落体冲击问题
设重量为P的重物，从高度h自由落下，冲击到等截 面直杆AB的B端。杆AB长度为l ，横截面面积为A。
A
A
A
P
h
B (a)
Fd
Δd
B (b)
三、动荷系数：
动荷系数 Kd
动响应 静响应
d Kdst
四、动应力分类：
1.简单动应力： 加速度可以确定的，采用“动静法”求解。 2.冲击载荷： 速度在极短暂的时间内有急剧改变，此时，加 速度不能确定，要采用“能量法”求之；
3.交变应力： 应力随时间作周期性变化，疲劳问题。
§6－2 构件有加速度时动应力计算
P
Δst
B
(c)
假设：1.冲击物变形与回弹可忽略。 2.AB杆质量可忽略。 3.冲击过程的能量耗散可忽略。
则当冲击物速度降为零时，杆AB发生最大伸长d ，
则冲击物减少的势能为
Ep P(hΔd)
(b)
而冲击物的初速与终速均为零，故
Ek 0
(c)
杆内应变能
Vεd
EA 2l
Δd2
(d)
将(b)(c)(d)代入(a)得
d Kdst
(1)
当 h0 时，相当于P 骤加在杆件上，这时
Kd 2
对于实际情况，以上计算是偏于安全的。
例6-5 已知：d1=0.3m, l=6m, P=5kN, E1=10Gpa, 求两种情况的动应力。（1）H=1m自由下落；（2） H=1m, 橡皮垫d2=0.15m, h=20mm,E2=8Mpa.
分析力学基础
分析力学基础-6 动载荷，交变应力
§6－1 概 述
一、静载荷与动载荷： 载荷不随时间变化（或变化极其平稳缓慢）且使构件各部件加速度保持为零（或可 忽略不计），此类载荷为静载荷。 载荷随时间急剧变化且使构件的速度有显著变化（系统产生惯性力），此类载荷为 动载荷。
二、动响应： 构件在动载荷作用下产生的各种响应（如应力、应变、位移等），称为动响应。 实验表明：在静载荷下服从虎克定律的材料，只要应力不超过比例极限 ,在动载荷 下虎克定律仍成立且E静=E动。
dm , a xKd ma x(1g a)M W m z ax
6q st
2q st M 图（ N·m)
(c)
由工字钢的弯矩图(图c)可知，Mmax=6qstN·m ，并由 型钢表查得Wz=21.210-6 m3以及已知数据代入上式， 得
(6 2.5 0 9 .8)N 1m
dm , a x 2 .022.2 1 1 6 0 m 3 1M 15Pa
FNd
P
P g
a
0
FNd
P
P a P(1 g
a) g
P
(2)钢索横截面的动应力：
P a dF A Nd P A(1a g)s(t1a g) g
令
Kd
1
a g
称为动荷因数，则
d Kdst
梁的弯矩：
MdmaxKdMstKd4Pl
梁的最大动应力：
dmaxMW dmaxK4dW Pl
例6-2 长度 l=12m 的16号工字钢，用横截面面积为 A=108mm2 的钢索起吊，如图a所示，并以等加速度 a=10m/s2 上升。若只考虑工字钢的重量而不计吊索 自重，试求吊索的动应力，以及工字钢在危险点的动
二、转动构件的动应力:
例6-3 重为G的球装在长L的转臂端部，以等角速度
在光滑水平面上绕O点旋转， 已知许用强度[] ，求
转臂的截面面积（不计转臂自重）。
O
L
FNd
解：①受力分析如图:
惯性力：
FNdmna2Rm 2LG /g
②强度条件
F N/dA
A
FNd
2GL
(g)
例6-4 设圆环的平均直径D、厚度t ，且 t«D，环的 横截面面积为A，单位体积重量为 ，圆环绕过圆心 且垂直于圆环平面的轴以等角速度旋转，如图所示
P(hΔd)E2lAΔd2 Pl
注意 EA ，Δst即在静载P下AB杆的伸长，则上式可
简化成
Δ d 22Δ sΔ td2Δ sh t 0
解出 d 的两个根，取其中大于 st 的那个根，即得
Δd Δst(1
1 2h) Δst
引用记号
2h
Kd (1
1 ) Δst
则
Δd KdΔst
(e)
将上式两边乘以 E/l 后得
qqstqd qst(1ga)
引入动荷因数
a Kd 1 g
则 qKdqst
由对称关系可知，两吊索的轴力 （F N参见图b）相
等，其值可由平衡方程 ，Fy 0 2FNqslt 0
求得
FN
1 2
qstl
Fq
N
st
F
N
(b)
A
B
吊索的静应力为
FN qstl
A 2A
故得吊索的动应力为 d Kd(1ga)q2sAtl
P H
d1
P
解：（1）
d2
h
st
Pl E1 A1
=0.0425 mm
d1 l
2H
Kd 1
1 st
218
dKdst1.5 4M 2 Pa
(2)
由型钢表查得 qst=20.5kg/m=(20.5N/m)g及已知数 据代入上式，即得
d (1 9 1 .8 m m 0 1 2 2)/ /( s 2 s.5 2 0 9 1 .8N 0 1 1) 6 8 1 /0 (m 2 ) 2.6 M 2 Pa
同理，工字钢危险截面上危险点处的动应力
应力d,max
2m 4m 4m 2m
(a) a
A
C
B
2.484m 7.032m 2.484m
(d)
A
B
z y
解：将集度为 qd=Aa 的惯性力加在工字钢上，使工
字钢上的起吊力与其重量和惯性力假想地组成平衡力
系。若工字钢单位长度的重量记为 qst ，则惯性力集 度为
qd
qst
a g
于是，工字钢上总的均布力集度为