3-3双原子分子的结构和性质

《分子的空间结构》第一课时教学设计积极性。

讲授新课第二节分子的空间结构第一课时分子结构的测定一、分子结构的测定早年的科学家主要靠对物质的化学性质进行系统总结得出规律后推测分子的结构。

如今，科学家应用了许多测定分子结构的现代仪器和方法，如红外光谱、晶体X射线衍射等。

下面先介绍红外光谱，下一章还将介绍晶体X射线衍射。

1.测定分子结构的现代仪器和方法红外光谱：分子中的原子不是固定不动的，而是处于不断振动着的。

红外线透过分子时，分子会吸收跟它的某些化学键的振动频率相同的红外线，再记录到谱图上呈现吸收峰。

通过和已有谱图库比对，或通过量子化学计算，可以得知分子中含有何种化学键或官能团的信息。

红外光谱仪原理示意图测分子体结构：红外光谱仪→吸收峰→分析官能团、化学键。

例如，通过红外光谱仪测得某未知物的红外光谱图如上图所示，发现有O—H、C—H、和C—O的振动吸收。

因此，可以初步推测该未知物中含有羟基（—OH）。

认真思考了解分子结构的测定方法。

了解红外光谱和质谱工作原理及应用。

【思考】红外光谱帮助我们确定分子中的化学键和官能团，还有什么现代化仪器帮我们确定有机物的结构呢？现代化学常利用质谱仪测定分子的相对分子质量。

质谱仪的基本原理是：在质谱仪中使分子失去电子变成带正电荷的分子离子和碎片离子等粒子。

由于生成的离子具有不同的相对质量，它们在高压电场加速后，通过狭缝进入磁场得以分离，在记录仪上呈现一系列峰，化学家对这些峰进行系统分析，便可得知样品分子的相对分子质量。

质谱：纵坐标表示相对丰度，横坐标表示粒子的相对质量与其电荷数之比（m/z），简称荷质比，化学家通过分析得知，被测物的相对分子质量是92，该物质是甲苯。

思考二、多样的分子空间结构在多原子构成的分子中，由于原子间排列的空间顺序不一样，于是分子就有了原子的几何学关系和形状，这就是分子的空间结构。

这就是分子的立体构型。

1.双原子分子（直线形）2.三原子分子的空间构型3.四原子分子的空间构型4.四原子分子其他立体构型（直线形、正四面体形）5..五原子分子的空间构型6.其他多原子分子认真思考通过对典型分子空间结构的学习，认识微观结构对分子空间结构的影响，了解共价分子结构的多样性和复杂性。

双原子分子理想气体的亥姆霍兹自由能1. 概述双原子分子理想气体是物理学中一个重要的研究对象。

在热力学和统计力学中，研究理想气体的性质对于理解气体行为和热力学过程具有重要意义。

亥姆霍兹自由能是描述理想气体的一个重要物理量，它在描述气体的热力学性质以及进行热力学计算时起着至关重要的作用。

本文将重点介绍双原子分子理想气体的亥姆霍兹自由能及其相关理论。

2. 双原子分子理想气体的特性双原子分子理想气体是由由两个原子构成的分子组成的气体。

在理想气体的假设下，双原子分子理想气体的分子之间不存在相互作用力，分子呈自由运动状态。

双原子分子理想气体的热力学性质和行为受到温度、压强、体积等多种因素的影响。

3. 亥姆霍兹自由能的定义亥姆霍兹自由能是热力学中的一个重要概念。

它表示了一个系统在恒定温度下，除去体积和能量的影响所剩余的可用于做非体积非能量的功的能量。

对于双原子分子理想气体，亥姆霍兹自由能的定义可以表达为以下公式：\[ F = U - TS \]其中，F表示亥姆霍兹自由能，U表示内能，T表示温度，S表示熵。

4. 亥姆霍兹自由能的物理意义亥姆霍兹自由能的物理意义在于描述了一个系统在恒定温度下可用于做非体积非能量的功的能量。

在平衡态下，系统的亥姆霍兹自由能取得最小值，因此通过对亥姆霍兹自由能进行热力学计算可以推导出系统的稳定性和平衡条件。

5. 双原子分子理想气体的亥姆霍兹自由能表达式对于双原子分子理想气体，亥姆霍兹自由能表达式可以表示为：\[ F = NkT \ln\left(\frac{V}{N}\left(\frac{2\pimkT}{h^2}\right)^{\frac{3}{2}}\right) \]其中，F表示亥姆霍兹自由能，N表示气体的摩尔数，k表示玻尔兹曼常数，T表示温度，V表示体积，m表示分子的质量，h表示普朗克常数。

6. 双原子分子理想气体的亥姆霍兹自由能的计算通过上述的亥姆霍兹自由能表达式，可以对双原子分子理想气体的亥姆霍兹自由能进行计算。

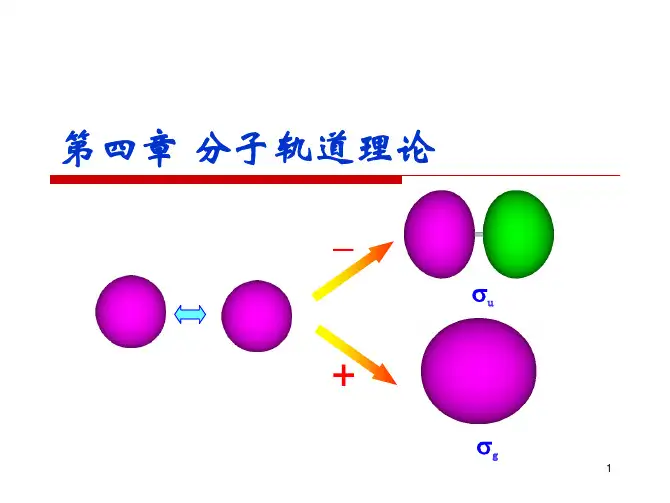
第三章双原子分子的结构和性质习题第三章共价键和双原子分子的结构习题一、是非题1．在LCAO-MO 中，所谓对称性匹配就是指两个原子轨道的位相相同。

2．两个能量不同的原子轨道线性组合成两个分子轨道。

在能量较低的分子轨道中，能量较低的原子轨道贡献较大；在能量较高的分子轨道中，能量较高的原子轨道贡献较大。

3．凡是成键轨道都具有中心对称性。

二、填空题1．描述分子中_______________空间运动状态的波函数称为分子轨道。

2．由原子轨道有效地形成分子轨道的条件为。

3．设φA 和φB 分别是两个不同原子A 和B 的原子轨道，其对应的原子轨道能量为E A 和E B ，如果两者满足________，____________，______原则可线性组合成分子轨道=c A φA +c B φB 。

对于成键轨道，如果E A ______E B ，则c A ______c B 。

(注：后二个空只需填"="，">"或"等比较符号)4．C 2+的分子轨道为_________________，键级___________________；5．按照简单分子轨道理论：(1)HF 分子基组态电子排布为___________________________，键级_______________，磁性________________。

(2)O 2-离子基组态电子排布为_____________________________，键级_______________，磁性________________。

6．写出CN -的价电子组态及键级。

7．下列分子中，键能比其正离子的键能小的是____________________。

键能比其负离子的键能小的是________________________。

O 2，NO ，CN ，C 2，F 28．O 2的键能比O 2+的键能_____________。

第三章 双原子分子结构3.1 +2H 的结构及共价键的本质基本内容—、定核近似和+2H 的薛定谔方程A BRe r e r e m H b a 02020*******ˆπεπεπε+--∇-= 我们常采用原子单位：单位长度：Pm e m h a e 9177.524422200==ππε（玻尔半径）单位质量：me=9.1095×10-31Kg （电子质量） 单位电荷:e=1.60219×10-19C （电子电量） 单位能量：024a e πε=27.2116eV单位角动量: =1.0546×10-34 J.S 单位介电常数:04πε=1采用原子单位、+2H 的哈密顿算符为：Rr r Hba 11121ˆ2+--∇-=其薛定谔方程为：ψψE Rr r b a =+--∇-)11121(2，式中E 、ψ分别为+2H 的波函数和能量。

二、变分原理及性线变分法 1． 变分原理对于任意一个品优波函数ψ，用体系的Hˆ算符求得的能量平均值将大于或接近等于体系基态的能量E 0即：*ˆ*E d d H E ≥>=<⎰⎰τψψτψψ 据此原理，利用求极值方法调节参数，找出能量最低时对应的波函数，即为和体系基态相近似的波函数。

2． 线性变分法在量化计算中，广泛采用的是线性变分函数，它是满足体系边界条件的 个线性无关的函数m φφφ,,,21 的线性组合:m m C C C φφφψ+++= 2211采用线性变分函数的变分法叫线性变分法。

根据变分原理求得使E 最低的一组组合系数Ci⎰⎰++++++++++++=τφφφφφφτφφφφφφd C C C C C C d C C C H C C C E m m mm m m m m ))(()(ˆ)(2211***2*2*1*12211***2*2*1*1mC EC E C E ∂∂==∂∂=∂∂ 21=0 由此得一组求解Ci 的m 个联立方程称为久期方程，运用线性代数法求得m 套非零解，由其中与最低E 相对应的一套解C 1,C 2,……,C m 便可组成基态分子轨道波函数，所对应的E 便是基态能量近似值。

应用分子轨道理论处理双原子分子结构1101班阮赛摘要：分子轨道理论（MO理论）是处理双原子分子及多原子分子结构的一种有效的近似方法，是化学键理论的重要内容。

它注重于分子轨道的认知，即认为分子中的电子围绕整个分子运动,注意了分子的整体性，因此较好地说明了多原子分子的结构。

目前，该理论在现代共价键理论中占有很重要的地位。

本文就分子轨道理论介绍及应用于双原子分子的一些内容作简单介绍。

关键词：分子轨道理论、、成建轨道、反键轨道、对称性匹配、最大重叠、能量相近, σ键、π键、键级、顺磁性、反磁性等。

背景:从20世纪30年代初，由Hund，Mulliken，Lennard-Jones开创，Slater，Hückel，Pople发展至今。

该方法的分子轨道具有较普通的数学形式，较易程序化。

六十年代以来，随着计算机的发展，该方法得到了很大的发展。

如Pople等研制的Gaussian从头算程序, 已成为当今研究化学键理论的主流方法.一、分子轨道理论（Molecular orbital theory）要点1、分子轨道理论的基本观点是把分子看作一个整体，其中电子不再从属于某一个原子而是在整个分子的势力场范围内运动。

正如在原子中每个电子的运动状态可用波函数（ψ）来描述那样，分子中每个电子的运动状态也可用相应的波函数来描述。

2、分子轨道是由分子中原子的原子轨道线性组合而成，简称LCAO (linear combination of atomic orbitals 的缩写)。

组合形成的分子轨道数目与组合前的原子轨道数目相等。

如两个原子轨道ψa和ψb线性组合后形成两个分子轨道ψ1和ψ2ψ1 = c1ψa +c2ψb ；ψ2= c1ψa -c2ψb这种组合和杂化轨道不同，杂化轨道是同一原子内部能量相近的不同类型的轨道重新组合，而分子轨道却是由不同原子提供的原子轨道的线性组合。

原子轨道用s、p、d、f……表示，分子轨道则用σ、π、δ……表示。

第3章双原子分子的结构与分子光谱习题答案1. CO是一个极性较小的分子还是极性较大的分子？其偶极距的方向如何？为什么？解：CO是一个异核双原子分子。

其中氧原子比碳原子多提供2个电子形成配位键：:O氧原子的电负性比碳C:原子的高，但是在CO分子中，由于氧原子单方面向碳原子提供电子，抵消了部分碳氧之间的电负性差别引起的极性，所以说CO是一个极性较小的分子。

偶极矩是个矢量，其方向是由正电中心指向负电中心，CO 的偶极距 = 0.37×10-30 C·m，氧原子端显正电，碳原子端显负电，所以CO 分子的偶极距的方向是由氧原子指向碳原子。

2. 在N2，NO，O2，C2，F2，CN，CO，XeF中，哪几个得电子变为AB-后比原来中性分子键能大，哪几个失电子变为AB+后比原来中性分子键能大？解：就得电子而言，若得到的电子填充到成键电子轨道上，则AB-比AB 键能大,若得到得电子填充到反键分子轨道上，则AB -比AB 键能小。

就失电子而言，若从反键分子轨道上失去电子，则AB +比AB 键能大，若从成键轨道上失去电子，则AB +比AB 键能小。

基态价电子组态为： (1)2g 4u 2u 2g 2)2()1()1()1(:N σπσσ 键级为3 1g 4u 2u 2g 2)2()1()1()1(:N σπσσ+ 键级为2.5 1u 2g 4u 2u 2g 2)2()2()1()1()1(:N πσπσσ- 键级为2.5N 2的键能大于N 2+和N 2-的键能（按N 2能级次序）(2) 12422)2()3()1()2()1(:NO πσπσσ 键级为2.52422)3()1()2()1(:NO σπσσ+键级为322422)2()3()1()2()1(:NO πσπσσ- 键级为2所以NO 的键能小于 NO +的键能，大于NO -的键能 (3)z x y x2*2222*122s 2s2p 2p 2p 2p O :()()()()()()+σσσπππ键级为2.5，z x y xy2*2222*1*122s 2s2p 2p 2p 2p 2p O :()()()()()()()σσσππππ键级为2，z x y xy2*2222*2*122s 2s2p 2p 2p 2p 2p O :()()()()()()()-σσσππππ键级为1.5，所以O 2的键能小于O 2+的键能，大于O 2-的键能 (4)4222)1()1()1(:u u g C πσσ 键级为23u 2u 2g 2)1()1()1(:C πσσ+键级为1.5 1g 4u 2u 2g 2)2()1()1()1(:C σπσσ-键级为2.5所以C 2的键能大于C 2+的键能，小于C 2 (5) 4*p 24p 22p 22*s 22s 22)()()()()(:F z ππσσσ 键级为13*p 24p 22p 22*s 22s 22)()()()()(:F z ππσσσ+键级为1.5 1p 24*p 24p 22p 22*s 22s 22)()()()()()(:F z z *-σππσσσ 键级为0.5所以F 2 的键能小于F 2+的键能，大于F 2-的键能CN 基态价电子组态（按N 2能级次序排列） (6)()()()()14223121:CN σπσσ 键级为2.5()()()()24223121:CN σπσσ- 键级为3()()()422121:CN πσσ+键级为2所以CN的键能大于CN+的键能，小于CN-的键能(7) CO基态价电子组态（按N2能级次序排列）2)224COσπσσ)1(:2(3()1()键级为32)+421COσπσσ1(:3()1())2(键级为2.52)-2412σCOππσσ1(:))2(3()2()1(键级为2.5所以CO的键能大于CO+和CO-的键能（按F2能级次序排列）(8)222441XeF:(1)(2)(3)(1)(2)(4)σσσππσ键级为0.544222)2()1()3()2()1(:F Xe ππσσσ+键级为1222442XeF :(1)(2)(3)(1)(2)(4)-σσσππσ键级为0所以XeF 的键能小于XeF +的键能，大于XeF -的键能，XeF -不能稳定存在。

第三章共价键和双原子分子的结构化学共价键是指通过原子间电子的共享而形成的化学键。

在双原子分子中，共价键的形成决定了分子的结构和性质。

本章将介绍共价键的形成原理和双原子分子的结构化学。

一、共价键的形成原理共价键的形成建立在原子间电子的共享基础上。

在共价键形成的过程中，原子外层电子通过相互重叠形成电子云（共价键电子云），原子间的空间重叠区域形成化学键。

共价键的形成有以下几个原则：1.电子云的形成：共价键需要通过原子外层电子的相互重叠来形成电子云。

一般来说，只有原子外层电子的轨道重叠区域能形成共价键。

2.电子云的稳定性：电子云的形成需要遵循几何排列的稳定性原则。

最稳定的结构是能够使电子云尽可能远离彼此的排列方式。

3.化合价的确定：化合价是指元素在化合物中的价态，描述原子定位于化合物中的位置。

通过化合价的计算，可以确定原子的连接方式和分子的形状。

双原子分子是由两个原子通过共价键连接而成的分子。

根据化合价的计算和几何形状，双原子分子可以分为两类：线性分子和非线性分子。

1.线性分子：线性分子的两个原子处于同一直线上，化合价为2、例如，氧气（O2）和氮气（N2）都是线性分子。

2.非线性分子：非线性分子的两个原子不处于同一直线上，化合价大于2、根据电子对排斥原则和共价键电子云的稳定性原则，非线性分子可以进一步分为三类：线性三角形结构、四方形结构和梯形结构。

a.线性三角形结构：其中一个原子位于另外两个原子的中心位置，两个原子之间的倾斜角度约为180度。

例如，一氧化氮（NO）就是线性三角形结构。

b.四方形结构：原子之间的倾斜角度约为109.5度。

例如，四氟化硅（SiF4）就是四方形结构。

c.梯形结构：原子之间的倾斜角度约为120度。

例如，氯化锡（SnCl2）就是梯形结构。

通过分子结构的分析，可以确定双原子分子的性质。

例如，分子中化合价倾斜角度的不同会影响分子的极性和化学反应的活性。

总结：共价键是通过原子间电子的相互重叠形成的化学键，决定了分子的结构和性质。