结构力学第4章习题及参考答案(1)

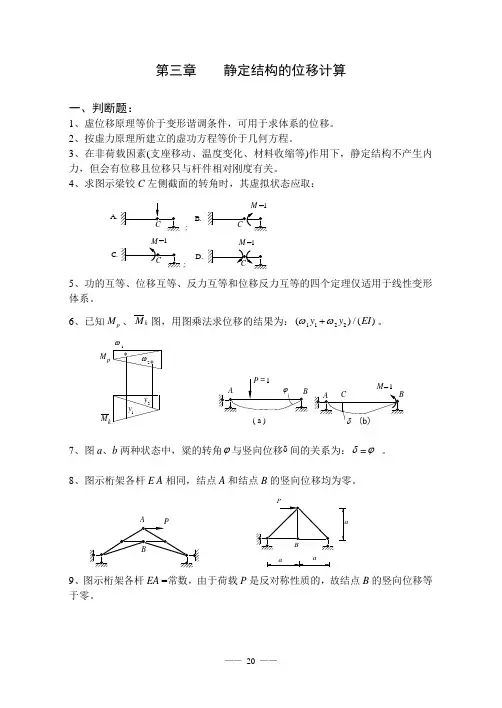
第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。

2、按虚力原理所建立的虚功方程等价于几何方程。

3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。

4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;;B.D.C.M =1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。

6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。

M kM p21y 1y 2**ωω( a )M 17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。

8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。

9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。

二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。

q11、求图示静定梁D 端的竖向位移 ∆DV 。

EI = 常数 ，a = 2m 。

10kN/m12、求图示结构E 点的竖向位移。

EI = 常数 。

ll l /32 /3/3q13、图示结构，EI=常数 ，M =⋅90kN m , P = 30kN 。

求D 点的竖向位移。

P14、求图示刚架B 端的竖向位移。

q15、求图示刚架结点C 的转角和水平位移，EI = 常数 。

q16、求图示刚架中Ｄ点的竖向位移。

EI ＝常数。

l/217、求图示刚架横梁中Ｄ点的竖向位移。

EI＝常数。

18、求图示刚架中D点的竖向位移。

E I = 常数。

qll l/l/2219、求图示结构Ａ、Ｂ两截面的相对转角，EI＝常数。

l/23l/320、求图示结构A、B两点的相对水平位移，E I = 常数。

ll21、求图示结构B点的竖向位移，EI = 常数。

ll22、图示结构充满水后，求A 、B 两点的相对水平位移。

结构力学 第四章习题 参考答案2005级4－1 图示抛物线拱的轴线方程24(fy x l l=−)x ，试求截面K 的内力。

解：（1） 求支座反力801155 kN 16AV AV F F ×=== 0805(5580)0.351500.93625 kN 16BV BV F F ×==−×+×== 0Mc 55880350 kN 4H F f ×−×===（2） 把及代入拱轴方程有:16m l =4m f =(16)16xy =−x （1）由此可得:(8)tan '8x y θ−==（2） 把截面K 的横坐标 ,代入（1），（2）两式可求得: 5m x ==＞, 3.44m y =tan 0.375θ= 由此可得:20.56θ= 则有sin 0.351θ=,cos 0.936θ=最后得出截面k 处的内力为: (上标L 表示截面K 在作用力左边，R 则表示截面在作用力右边)055550 3.44103 kN m K H M M F y =−=×−×=i0cos sin 550.936500.35133.93 kN L sK s H F F F θθ=−=×−×= (5580)0.936500.35140.95 kN R sK F =−×−×==40.95 KN 0sin cos 550.351500.93666.1 kN L NK s H F F F θθ=+=×+×= (5580)0.351500.93638.03 kN R NK F =−×+×=4－2 试求拉杆的半圆三铰拱截面K 的内力。

解：（1）以水平方向为X 轴,竖直方向为Y 轴取直角坐标系，可得K 点的坐标为：2m6mK K x y =⎧⎪⎨==⎪⎩ （2）三铰拱整体分别对A ，B 两点取矩，由平衡方程可解得支座反力：0 20210500 20210500 2100A By B Ay x Ax M F M F F F ⎧=×−××⎪⎪=×+××⎨⎪=−×=⎪⎩∑∑∑=== =＞ 5 kN ()20 kN () 5 kN ()Ay Ax By F F F =−⎧⎪=−⎨⎪=⎩向下向上向左（3）把拱的右半部分隔离，对中间铰取矩，列平衡方程可求得横拉杆轴力为：CN 0 105100MF =×−×∑=＞N 5 kN F =（4）去如图所示的α角，则有：=＞cos 0.6sin 0.8θθ=⎧⎨=⎩于是可得出K 截面的内力，其中：22(6)206525644 kN m 2K M ×=−+×−×−×=isK F (20265)sin 5cos 0.6 kN θθ=−×−×−×=− NK F (20265)cos 5sin 5.8 kN θθ=−−×−×−×=−13K M F r Fr ==（内侧受拉） K 截面作用有力，剪力有突变 且有01sin3032LSK 2F F F F =−=−×=− （2） 22R SK F FF F =−=（3）011sin30(326NKF F F F ==×=拉力）（4）4-4 试求图示三铰拱在均布荷载作用下的合理拱轴线方程。

结构力学第三版王焕定第4章习题及参考答案[1] 第3章3-1 试用直杆公式求图示圆弧型曲梁B 点水平位移。

EI 为常数。

解由图（a ）、（b ）可知结构在单位力和荷载作用下的内力都是对称的，所以可只对一半进行积分然后乘以2来得到位移。

令内侧受拉为正，则()P P sin 0,21cos 2M R F M R θπθθ?=∈=-??代入公式，得()()P P203P P 2d 2d 2sin 1cos d ? 22Bx MM MM s sEI EIF F R R R R EI EIππθθθ==?=?-=→∑* 3-2 图示柱的A 端抗弯刚度为EI ，B 端为EI /2，刚度沿柱长线性变化。

试求B 端水平位移。

解以左侧受拉为正，则[]30P 0,6M x x l q x M l ?=?∈?=代入公式，得3400P001d d 630ll Bxq x q l MM s x x EI EI l EI===??q 0习题3-2图l（b ）3-3 试求图示结构考虑弯曲变形和剪切变形的挠度曲线方程。

截面为矩形，k =。

解令上侧受拉为正，则单位力和荷载作用下的弯矩和剪力表达式分别为[]Q 2P QP ,10,,2M x F x l ql M qlx F ql ?==?∈?=-=??代入公式，得()Q QP P0024200d d 1 1.2 1.2d 1d 212ll By l l kF F MM x x EI GAql ql ql x qlx x ql x EI GA EI GA ?=+??=-+??=+↓ ??习题3-3 图22ql 22ql （b ）（a ）3-4 试求图示桁架C 点竖向位移和CD 杆与CE 杆夹角的改变量。

已知各杆截面相同，A =×10-2m 2，E =210 GP a 。

解（1）C 点的竖向位移()()92229222465112.5kN 6m 2125kN 5m 88 21010N/m 1.510m 53262.5kN 5m 275kN 6m8821010N/m 1.510m 6.39910mC y----?-?+?-?-? ? ???=+???+???=? （2）CD 杆与CE 杆夹角的改变量N 2N P 922252(0.15)62.5kN 5m 0.25(112.5kN )6m 21010N/m 1.510m 8.33310radCD CE F F l EA---=?-??+?-?==-?∑N P (b)kN F 图(）N2(c)F 图3 m ×4 习题3-5 图N1(a)F 图6-3-5 图示桁架AB杆的σ=，其他杆的Eσε=。

结构力学课程作业答案第一章绪论1、按照不同的构造特征和受力特点，平面杆件结构可分为哪几类？2、何为静定结构和超静定结构？从几何构造分析的角度看，结构必须是几何不变体系。

根据多余约束 n ，几何不变体系又分为：有多余约束( n > 0)的几何不变体系——超静定结构；无多余约束( n = 0)的几何不变体系——静定结构。

从求解内力和反力的方法也可以认为：静定结构：凡只需要利用静力平衡条件就能计算出结构的全部支座反力和杆件内力的结构。

超静定结构：若结构的全部支座反力和杆件内力，不能只有静力平衡条件来确定的结构。

3、土建、水利等工程中的荷载，根据其不同的特征，主要有哪些分类？第二章平面结构的几何组成分析作业题：1、何为平面体系的几何组成分析？按照机械运动及几何学的观点，对平面结构或体系的组成情况进行分析，称为平面体系的几何组成分析。

2、何为几何不变体系？何为几何可变体系？几何不变体系—若不考虑材料的应变，体系的位置和形状不会改变。

几何可变体系—若不考虑材料的应变，体系的位置和形状是可以改变的。

3、几何组成分析的目的是什么？1）保证结构的几何不变性,以确保结构能承受荷载和维持体系平衡.2）判别某一体系是否为几何不变,从而决定它能否作为结构.3）研究几何不变体系的组成规则,以保证所设计的结构是几何不变体系,从而能承受荷载而维持平衡.4）根据体系的几何组成分析,正确区分静定结构和超静定结构,从而选择适当的计算方法进行结构的反力和内力计算.5）通过几何组成分析,明确结构的构成特点,从而选择结构受力分析的顺序以简化计算.4、何为一个体系的自由度？知悉体系计算自由度的公式。

5、试对下图所示体系进行几何组成分析。

图1图2图3图46、试求图示各体系的计算自由度数W。

7、例2-1 例2-28、习题 2.1～2.12 试对图示体系作几何组成分析。

第三章静定梁、静定平面刚架和三角拱的计算作业题：1、单跨静定梁有简支梁、外伸梁、悬臂梁等形式。

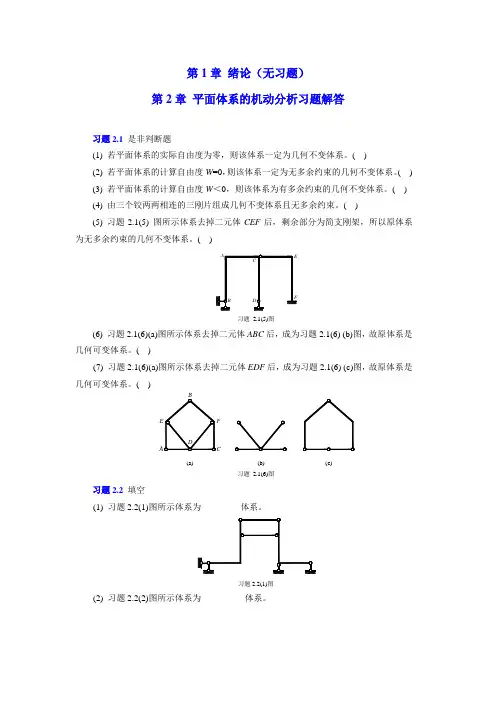
第1章绪论（无习题）第2章平面体系的机动分析习题解答习题2.1是非判断题(1) 若平面体系的实际自由度为零，则该体系一定为几何不变体系。

( )(2) 若平面体系的计算自由度W=0，则该体系一定为无多余约束的几何不变体系。

( )(3) 若平面体系的计算自由度W＜0，则该体系为有多余约束的几何不变体系。

( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。

( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。

( )习题2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后，成为习题2.1(6) (b)图，故原体系是几何可变体系。

( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后，成为习题2.1(6) (c)图，故原体系是几何可变体系。

()(a)(b)(c)习题2.1(6)图习题2.2填空(1) 习题2.2(1)图所示体系为_________体系。

习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。

习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。

习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。

习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。

习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系，有_________个多余约束。

习题2.2(6)图(7) 习题2.2(7)图所示体系为_________体系，有_________个多余约束。

习题2.2(7)图习题2.3对习题2.3图所示各体系进行几何组成分析。

(a)(b)(c)(d)(e)(f)(h)(g)(i)(j)(k)(l)习题2.3图第3章 静定梁与静定刚架习题解答习题3.1 是非判断题(1) 在使用内力图特征绘制某受弯杆段的弯矩图时，必须先求出该杆段两端的端弯矩。

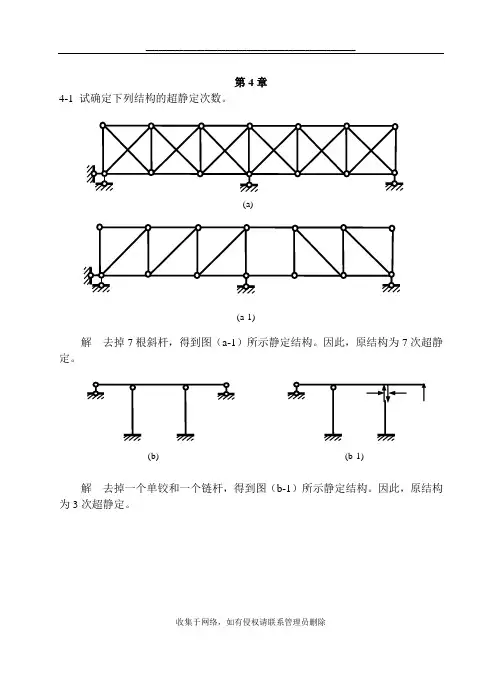
第4章4-1 试确定下列结构的超静定次数。

解 去掉7根斜杆，得到图（a-1）所示静定结构。

因此，原结构为7次超静定。

解 去掉一个单铰和一个链杆，得到图（b-1）所示静定结构。

因此，原结构为3次超静定。

(a)(a-1) (b)(b-1)解 去掉三个水平链杆，得到图（c-1）所示静定结构。

因此，原结构为3次超静定。

解 去掉两个单铰，得到图（d-1）所示静定结构。

因此，原结构为4次超静定。

解 去掉两个单铰，切断一个梁式杆，得到图（e-1）所示静定结构。

因此，原结构为7次超静定。

(d)(e) (c)(c-1)(d-1)(e-1)解 去掉四个支链杆，切断两个梁式杆，得到图（f-1）所示静定结构。

因此，原结构为10次超静定。

解 去掉一个单铰，两个链杆，切开一个封闭框，得到图（g-1）所示静定结构。

因此，原结构为7次超静定。

解 切开七个封闭框，得到图（g-1）所示静定结构。

因此，原结构为21次超静定。

(f)(g) (h)(f-1)(g-1)(h-1)2/8M 图解 切开两个封闭框，得到图（i-1）所示静定结构。

因此，原结构为6次超静定。

4-2 试用力法计算下列超静定梁，并作M 和F Q 图。

EI 为常数。

解 1111P 0X δ∆+= 34111P 13388l ql ql X EIEIδ∆-===(i)qq A2/2M P 图1(i-1)4-2 (b)解1111221P 2112222P 0X X X X δδ∆δδ∆++=++=2P 112212211P 2P 3616F l l lEI EI EIδδδδ∆∆-======，， P 12 8F lX X ==基本体系PM P 图2M 图1M 图F P l l /8 M 图F P l /84-2(c)解 1111P 0X δ∆+=；2P 111P 2F l lEI EIδ∆==、；P 12F l X -=。

（c ）X 1基本体系P M P 图PF P l /2图M1M 图X 1=114-2 (d)解 1111P 0X δ+∆=；3111P 1213324l l ql EI EI EI δ=+∆=-， k =10时：32111P 22113024088l ql ql X EI EI δ=∆=-=1，， k ＝0.1时：32111P 1221110532444l ql ql X EI EI δ=∆=-=，， (d) I 1=kI 2，①k =10，②k =0.1基本体系25ql2ql 8M P 图4-3 试用力法计算下列超静定刚架，并作弯矩图。

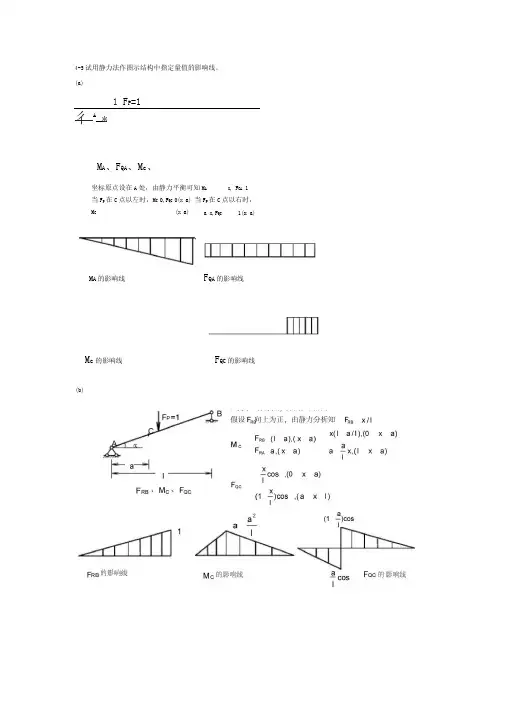
4-5试用静力法作图示结构中指定量值的影响线。

(a)1 F P=1彳A*M A、F QA、M c、坐标原点设在A处，由静力平衡可知M A X,F CA 1当F p在C点以左时，M C O,F QC 0(X a) 当F p在C点以右时，M C(X a)F QC的影响线(b)M A的影响线F QA的影响线a X,F QC1(x a) M c的影响线由M EM CM B0知,F NCDFNCD3535(d)F QC RF NCD | 4 12 (5 x),(02,(5 XX 3)7)X 3,(00,(3 X二F NCD5一F NCD,(3 x51,(07)7)3)(7 X) 03474F NCD35125—X125)1評0-x,(343)7)的影响线『尸11F QC R的影响线以D点为坐标原点，向右为正—4m5m -2m**H2m**---- 5m—F RB X 1「X 1 L 1 X〒,M C 〒，F QCM C、F QCM c的影响线F QC的影响线(e)|F P=1A t aB rxJ；D-^Jz 4a A* 2aF Q A、F Q A、F QC、M eF Q A1,(00,(aa)匚R，F QA7a)0,(0 x1,(a xa)7a)F QC0,(01,(5a 5a)7a)，Mcx a,(04a,(5ax 5a)x 7a)(f)FRA|F P=1—a 江卜a -**j* a a ■卜F RA、F QB、M E、F QF M Ei2>0,(2a xx小-,(0 x2x .a 2，(a0,(2a xx 2a) F，F QB知0 x 2 a)5a) 0,(2 a x 5a)a)x—,(0 x4a2a)x 2a), F QF 3 X-—,(2ax 4a)5a)5 x-—,(4a2 2ax 5a)F RA的影响线F QB的影响线a/2ME的影响线4-6试用机动法作图示结构中指定量值的影响线。

(a)F p=11/21/21/4(C)F p =14-7试绘制图示结构主梁指定量值的影响线，并加以比较。

结构力学课后习题答案4结构力学课后习题答案4结构力学是工程学中非常重要的一门学科，它研究物体在受到外力作用下的变形和破坏行为。

通过学习结构力学，我们可以更好地理解和分析各种工程结构的力学性能，为工程设计和施工提供有力的支持。

下面是结构力学课后习题的答案，希望对大家的学习有所帮助。

1. 问题描述：一个悬臂梁的长度为L，横截面形状为矩形，宽度为b，高度为h。

在悬臂梁的自重作用下，梁的挠度为δ。

求悬臂梁在距离支点x处的弯矩M和剪力V。

解答：根据悬臂梁的受力分析，距离支点x处的弯矩M可以通过以下公式计算：M = -wLx + 1/2wL^2其中，w为单位长度的梁的自重。

剪力V可以通过以下公式计算：V = wL - wx2. 问题描述：一个梁的长度为L，横截面形状为矩形，宽度为b，高度为h。

在梁的两端分别施加一个向下的集中力P。

求梁在距离支点x处的弯矩M和剪力V。

解答：根据梁的受力分析，距离支点x处的弯矩M可以通过以下公式计算：M = -Px + P(L-x)剪力V可以通过以下公式计算：V = P3. 问题描述：一个梁的长度为L，横截面形状为矩形，宽度为b，高度为h。

在梁的两端分别施加一个向下的集中力P。

梁的弹性模量为E，截面惯性矩为I。

求梁在距离支点x处的挠度δ。

解答：根据梁的受力分析，梁在距离支点x处的挠度δ可以通过以下公式计算：δ = (Px(L^2-x^2))/(6EI)4. 问题描述：一个梁的长度为L，横截面形状为矩形，宽度为b，高度为h。

在梁的两端分别施加一个向下的集中力P。

梁的弹性模量为E，截面惯性矩为I。

求梁在距离支点x处的剪力V。

解答：根据梁的受力分析，梁在距离支点x处的剪力V可以通过以下公式计算：V = P(L-x)/L5. 问题描述：一个梁的长度为L，横截面形状为矩形，宽度为b，高度为h。

在梁的两端分别施加一个向下的集中力P。

梁的弹性模量为E，截面惯性矩为I。

求梁在距离支点x处的弯矩M。

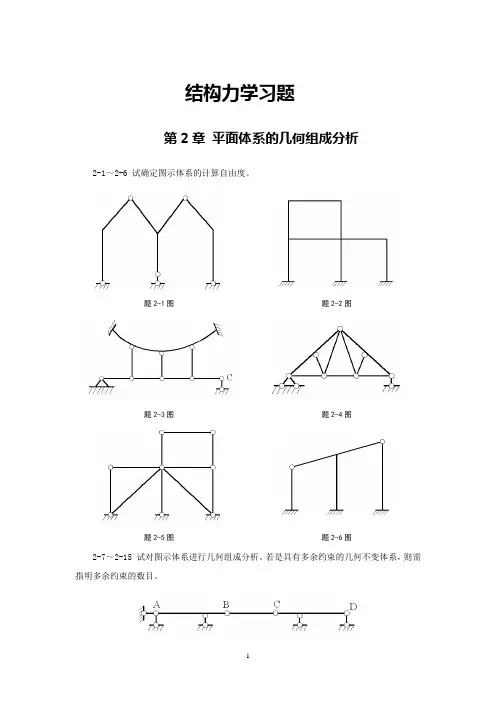
结构力学习题第2章平面体系的几何组成分析2-1～2-6 试确定图示体系的计算自由度。

题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7～2-15 试对图示体系进行几何组成分析。

若是具有多余约束的几何不变体系，则需指明多余约束的数目。

题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-1 1W=2-1 9-W=2-3 3-W=2-4 2-W=2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。

（a）（b）(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。

（a）（b）(c)习题3-2图3-3～3-9 试作图示静定刚架的内力图。

习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定结构的弯矩图是否正确。

(a)(b)(c)(d)部分习题答案3-1 （a ）m kN M B ⋅=80（上侧受拉），kN F RQB 60=，kN F L QB 60-=（b ）m kN M A ⋅=20（上侧受拉），m kN M B ⋅=40（上侧受拉），kN F RQA 5.32=，kN F L QA 20-=，kN F LQB 5.47-=，kN F R QB 20=(c) 4Fl M C =（下侧受拉），θcos 2F F L QC =3-2 (a) 0=E M ，m kN M F ⋅-=40（上侧受拉），m kN M B ⋅-=120（上侧受拉）（b ）m kN M RH ⋅-=15(上侧受拉)，m kN M E ⋅=25.11（下侧受拉）（c ）m kN M G ⋅=29(下侧受拉)，m kN M D ⋅-=5.8(上侧受拉)，m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10（左侧受拉），m kN M DF ⋅=8（上侧受拉），m kN M DE ⋅=20（右侧受拉） 3-4 m kN M BA ⋅=120（左侧受拉）3-5 m kN M F ⋅=40（左侧受拉），m kN M DC ⋅=160（上侧受拉），m kN M EB ⋅=80(右侧受拉) 3-6 m kN M BA ⋅=60（右侧受拉），m kN M BD ⋅=45（上侧受拉），kN F QBD 46.28=3-7 m kN M C ⋅=70下（左侧受拉），m kN M DE ⋅=150（上侧受拉），m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0（上侧受拉），m kN M BA ⋅=36.0（右侧受拉） 3-9 m kN M AB ⋅=10（左侧受拉），m kN M BC ⋅=10（上侧受拉） 3-10 （a ）错误 （b ）错误 （c ）错误 （d ）正确第4章 静定平面桁架和组合结构的内力分析4-1 试判别习题4-1图所示桁架中的零杆。

第1章 绪论（无习题）第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零，则该体系一定为几何不变体系。

( )(2) 若平面体系的计算自由度W =0，则该体系一定为无多余约束的几何不变体系。

( ) (3) 若平面体系的计算自由度W ＜0，则该体系为有多余约束的几何不变体系。

( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。

( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。

( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后，成为习题2.1(6) (b)图，故原体系是几何可变体系。

( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后，成为习题2.1(6) (c)图，故原体系是几何可变体系。

()(a)(b)(c)AEBFCD习题 2.1(6)图【解】（1）正确。

（2）错误。

0W 是使体系成为几何不变的必要条件而非充分条件。

（3）错误。

（4）错误。

只有当三个铰不共线时，该题的结论才是正确的。

（5）错误。

CEF 不是二元体。

（6）错误。

ABC 不是二元体。

（7）错误。

EDF 不是二元体。

习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。

习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。

习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。

习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。

习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。

习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系，有_________个多余约束。