工程力学(材料力学)-5-杆件的内力图
- 格式:ppt
- 大小:4.13 MB
- 文档页数:96


静力学部分第1章 工程静力学基础1、平面汇交力系如图所示,已知F 1=kN 3,F 2=1kN ,F 3=3kN ,则该力系的合力R 的大小应为( ) A 、R=(1+43) kN B 、R=kN 3C 、R=(1+23)kND 、R=02、重量为W 的物块放在倾角为θ的粗糙斜面上而处于临界平衡状态。
已知物块与斜面间的静滑动摩擦系数为f ,此时物块受到斜面的摩擦力为( )A 、FwB 、fW sin θC 、fW cos θD 、fW tan θ3、在图示轮子受力图中,Fr m Fr m 3,21==,其中( )图轮子处于平衡状态。
4、如图所示系统只受F 作用而处于平衡。
欲使A 支座约束反力的作用线与AB 成300角,则斜面的倾角α应为( )A 、00B 、300C 、450D 、 6005、平面汇交四个力作出如下图所示力多边形,表示力系平衡的是( ).6、若作用在A 点的两个大小不等的力1F 和2F ,沿同一直线但方向相反。
则其合力可以表示为( )。
A 、12F F -;B 、21F F -;C 、12F F +。
7、重P的均质圆柱放在V型槽里,考虑摩擦柱上作用一力偶,其矩为M时(如图),圆柱处于极限平衡状态。
此时按触点处的法向约束力N A与N B的关系为()。
A、N A = N B;B、N A > N B;C、N A < N B。
8、图示三铰刚架,受水平力P作用,有以下四种说法,其中错的是()。
A、AC为二力平衡杆件B、BC为三力平衡构件C、反力RA和RB的方向都指向CD、RA的方向指向C,RB的方向不确定9、如果力FR 是F1、F2二力的合力,用矢量方程表示为FR=F1+F2,则三力大小之间的关系为( )。
A、必有FR =F1+F2B、不可能有FR=F1+F2C、必有FR >F1,FR>F2D、可能有FR<F1,FR<F210、力对物体的作用效应取决于力的三要素,下列选项中不属于力的三要素的是:(B )A、力的大小B、力的单位C、力的方向D、力的作用点11、刚体受三力作用而处于平衡状态,则此三力的作用线( A )。

《工程力学》第4次作业解答(杆件的内力计算与内力图)2008-2009学年第二学期一、填空题1.作用于直杆上的外力(合力)作用线与杆件的轴线重合时,杆只产生沿轴线方向的伸长或缩短变形,这种变形形式称为轴向拉伸或压缩。
2.轴力的大小等于截面截面一侧所有轴向外力的代数和;轴力得正值时,轴力的方向与截面外法线方向相同,杆件受拉伸。
3.杆件受到一对大小相等、转向相反、作用面与轴线垂直的外力偶作用时,杆件任意两相邻横截面产生绕杆轴相对转动,这种变形称为扭转。
4.若传动轴所传递的功率为P 千瓦,转速为n 转/分,则外力偶矩的计算公式为9549P M n=⨯。
5.截面上的扭矩等于该截面一侧(左或右)轴上所有外力偶矩的代数和;扭矩的正负,按右手螺旋法则确定。
6.剪力S F 、弯矩M 与载荷集度q 三者之间的微分关系是()()S dM x F x dx =、()()S dF x q x dx=±。
7.梁上没有均布荷载作用的部分,剪力图为水平直线,弯矩图为斜直线。
8.梁上有均布荷载作用的部分,剪力图为斜直线,弯矩图为抛物线。
9.在集中力作用处,剪力图上有突变,弯矩图上在此处出现转折。
10.梁上集中力偶作用处,剪力图无变化,弯矩图上有突变。
二、问答题1.什么是弹性变形?什么是塑性变形?解答:在外力作用下,构件发生变形,当卸除外力后,构件能够恢复原来的大小和形状,则这种变形称为弹性变形。
如果外力卸除后不能恢复原来的形状和大小,则这种变形称为塑性变形。
2.如图所示,有一直杆,其两端在力F 作用下处于平衡,如果对该杆应用静力学中“力的可传性原理”,可得另外两种受力情况,如图(b )、(c )所示。
试问:(1)对于图示的三种受力情况,直杆的变形是否相同?(2)力的可传性原理是否适用于变形体?解答:(1)图示的三种情况,杆件的变形不相同。
图(a )的杆件整体伸长变形,图(b )的杆件只有局部伸长变形,图(c )的杆件是缩短变形。


6 .剪力 F 、弯矩 M 与载荷集度 q 三者之间的微分关系是 dM ( x)= F ( x ) 、dx《工程力学》第 4 次作业解答(杆件的内力计算与内力图)2008-2009 学年第二学期一、填空题1.作用于直杆上的外力(合力)作用线与杆件的轴线重合时,杆只产生沿轴线方向的 伸长或缩短变形,这种变形形式称为轴向拉伸或压缩。
2.轴力的大小等于截面截面一侧所有轴向外力的代数和;轴力得正值时,轴力的方向 与截面外法线方向相同,杆件受拉伸。
3.杆件受到一对大小相等、转向相反、作用面与轴线垂直的外力偶作用时,杆件任意 两相邻横截面产生绕杆轴相对转动,这种变形称为扭转。
4.若传动轴所传递的功率为 P 千瓦,转速为 n 转/分,则外力偶矩的计算公式为M = 9549 ⨯ Pn。
5.截面上的扭矩等于该截面一侧(左或右)轴上所有外力偶矩的代数和;扭矩的正负, 按右手螺旋法则确定。
S S dF ( x )S dx= ±q ( x ) 。
7.梁上没有均布荷载作用的部分,剪力图为水平直线,弯矩图为斜直线。
8.梁上有均布荷载作用的部分,剪力图为斜直线,弯矩图为抛物线。
9.在集中力作用处,剪力图上有突变,弯矩图上在此处出现转折。
10.梁上集中力偶作用处,剪力图无变化,弯矩图上有突变。
二、问答题1.什么是弹性变形?什么是塑性变形?解答:在外力作用下,构件发生变形,当卸除外力后,构件能够恢复原来的大小和形状,则这种变形称为弹性变形。
如果外力卸除后不能恢复原来的形状和大小,则这种变形称为塑性变形。
2.如图所示,有一直杆,其两端在力 F 作用下处于平衡,如果对该杆应用静力学中“力的可传性原理”,可得另外两种受力情况,如图(b )、(c )所示。
试问:(1)对于图示的三种受力情况,直杆的变形是否相同? (2)力的可传性原理是否适用于变形体?问答题 2 图问答题 3 图。
解答:(1)图示的三种情况,杆件的变形不相同。





工程力学工程静力学与材料力学马志涛第5章杆件的内力图5.1.4 杆件内力分量的正负号规则5.1.4 杆件内力分量的正负号规则——轴力▪当轴力背离截面,即杆件受到拉伸时,其轴力为正。
▪当轴力指向截面,即杆件受到压缩时,其轴力为负。
F AB Fm m F N AFm m F B F N m m▪当轴力背离截面,即杆件受到拉伸时,其轴力为正。
▪当轴力指向截面,即杆件受到压缩时,其轴力为负。
FAB Fm mF NAFm mF BF Nm m▪使截开部分顺时针转动为正▪使截开部分逆时针转动为负FF mmFF SFF S▪使截开部分顺时针转动为正▪使截开部分逆时针转动为负FFmmFF SFF S凹面朝上的弯矩为正凹面朝下的弯矩为负M MM M▪按右手螺旋法则,扭矩T 的方向与截面外法线方向一致为正▪按右手螺旋法则,扭矩T 的方向与截面外法线方向相反为负M e M ennⅠⅡM eⅠTTM eⅡ▪按右手螺旋法则,扭矩T的方向与截面外法线方向一致为正▪按右手螺旋法则,扭矩T的方向与截面外法线方向相反为负M eⅠT TM eⅡM e MeⅠⅡnnC▪一直杆,A 端固定,在B 、C 两处作用有集中载荷F 1和F 2,其中F 1=5 kN ,F 2=10 kN 。
▪试画出:杆件的轴力图。
C AB F 1F 2llCAB llF 1F 2F A 解:1. 确定A 处的约束力A 处虽然是固定端约束,但由于杆件只有轴向载荷作用,所以只有一个轴向的约束力F A 。
由平衡方程求得F A =5 kNF x =0F A +F 1−F 2=0解:2.确定控制面3.应用截面法求控制面上的轴力用假想截面分别从控制面A 、B'、B"、C 处将杆截开,假设横截面上的轴力均为正方向(拉力),并考察截开后下面部分的平衡。
C ABF 1F 2llCAB llF 1F 2F A在集中载荷F 2、约束力F A 作用处的A 、C 截面,以及集中载荷F 1作用点B 处的上、下两侧横截面都是控制面。
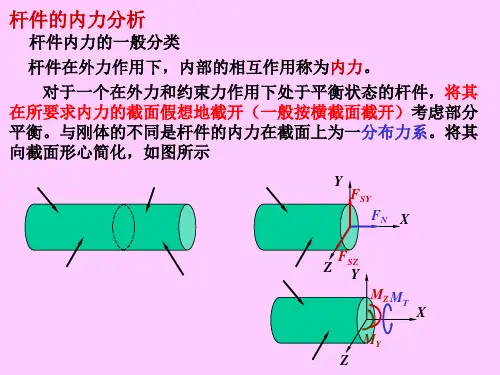
第五章杆件的内力分析在进行结构设计时,为保证结构安全正常工作,要求各构件必须具有足够的强度和刚度。
解决构件的强度和刚度问题,首先需要确定危险截面的内力。
内力计算是结构设计的基础。
本章研究杆件的内力计算问题。
第一节杆件的外力与变形特点进行结构的受力分析时,只考虑力的运动效应,可以将结构看做是刚体;但进行结构的内力分析时,要考虑力的变形效应,必须把结构作为变形固体处理。
所研究杆件受到的其他构件的作用,统称为杆件的外力。
外力包括载荷(主动力)以及载荷引起的约束反力(被动力)。
广义地讲,对构件产生作用的外界因素除载荷以及载荷引起的约束反力之外,还有温度改变、支座移动、制造误差等。
杆件在外力的作用下的变形可分为四种基本变形及其组合变形。
一、轴向拉伸与压缩受力特点:杆件受到与杆件轴线重合的外力的作用。
变形特点:杆沿轴线方向的伸长或缩短。
产生轴向拉伸与压缩变形的杆件称为拉压杆。
图:5-1所示屋架中的弦杆、牵引桥的拉索和桥塔、阀门启闭机的螺杆等均为拉压杆。
图5-1二、剪切受力特点:杆件受到垂直杆件轴线方向的一组等值、反向、作用线相距极近的平行力的作用。
变形特点:二力之间的横截面产生相对的错动。
产生剪切变形的杆件通常为拉压杆的连接件。
如图5-2所示螺栓、销轴连接中的螺栓和销钉,均产生剪切变形。
图5-2三、扭转受力特点:杆件受到作用面垂直于杆轴线的力偶的作用。
变形特点:相邻横截面绕杆轴产生相对旋转变形。
产生扭转变形的杆件多为传动轴,房屋的雨蓬梁也有扭转变形,如图:5-3所示。
图5-3四、平面弯曲受力特点:杆件受到垂直于杆件轴线方向的外力或在杆轴线所在平面内作用的外力偶的作用。
变形特点:杆轴线由直变弯。
各种以弯曲为主要变形的杆件称为梁。
工程中常见梁的横截面多有一根对称轴(图5-4)各截面对称轴形成一个纵向对称面,梁的轴线也在该平面内弯成一条曲线,这样的弯曲称为平面弯曲。
如图5-4所示。
平面弯曲是最简单的弯曲变形,是一种基本变形。