简谐振动的运动方程166页PPT

通过图表展示实验结果，如位移-时间 图、速度-时间图等，以便更直观地分 析振动特性。
波动方程验证性实验设计思路分享
实验目的通过观察Βιβλιοθήκη 测量波动现象，验证波动方程的正确性。
实验原理
利用波动方程描述波的传播规律，通过实验数据验证理论预测。
波动方程验证性实验设计思路分享
实验设计思路
选择合适的波动源和测量仪器，如振动台、激光 干涉仪等。
01
实验步骤
02
搭建实验装置，包括弹簧、振子、测量仪器等。
调整实验参数，如弹簧劲度系数、振子质量等，以获得不同条
03
件下的振动数据。
弹簧振子实验设计思路分享
使用测量仪器记录振动的位移、速度 、加速度等数据。
对实验数据进行处理和分析，提取简 谐振动的基本特征。
单摆实验数据处理技巧指导
实验目的
通过观察和测量单摆的运动，研究简谐振动的基本规律。
波动传播速度
波动在介质中传播的速度称为波动传播速度。对于简谐振动 形成的机械波而言，波动传播速度与介质的性质有关，如弹 性模量、密度等。同时，波动传播速度还与振动的频率有关 ，频率越高则波动传播速度越快。
02
简谐振动的动力学特征
回复力与加速度关系
回复力定义
指向平衡位置的力，大小与位移成正比，方 向始终指向平衡位置。
1 研究非线性振动现象
通过设计和实施非线性振动实验，探索非线性振动的基 本规律和特性，如混沌现象、分岔行为等。
2 探究复杂系统中的振动传播
研究复杂网络中振动传播的动力学行为，揭示网络结构 对振动传播的影响机制。
3 开发新型振动传感器件
结合微纳加工技术和振动理论，设计并制作具有高灵敏 度、高分辨率的振动传感器件，应用于精密测量和工程 领域。

机械振动
第一节 简谐运动
高中阶段学过的运动形式有哪些?
• 匀速直线运动 • 特点: • 图象:
匀变速直线运动
特点:
图象:
Main Idea
运动的共同特点
一、机械振动：物体在某一位置附近 所做的往复运动
今天我们研究最简单、最基本的机械振动
－－简谐运动
二、弹簧振子
装置
运动特点：某一位置附近往复运动
10 5 0 -5 -10
1 2
3
4
5 6 t/s
2、某弹簧振子的振动图象如图所示，根据图象判断。下 列说法正确的是（D ） A、第1s内振子相对于平衡位置的位移与速度方向相反 B、第2s末振子相对于平衡位置的位移为-20cm C、第2s末和第3s末振子相对于平衡位置的位移均相 同，但瞬时速度方向相反 D、第1s内和第2s内振子相对于平衡位置的位移方向 相同，瞬时速度方向相反。 x/cm
２、简谐运动的图象
图象坐标轴的含义
图象的形状：正弦或余弦曲线 图象的物理意义 举例分析 20 x/cm
0 1
-20
2
3
4
5
6
7 t/s
课堂练习
1、某一弹簧振子的振动图象如图所示，则由 图象判断下列说法正确的是（A B ） A、振子偏离平衡位置的最大距离为10cm B、1s到2s的时间内振子向平衡位置运动 C、2s时和3s时振子的位移相等，运动方向 也相同 x/cm D、振子在2s内完 成一次往复性运动
平衡位置 －－合外力为零 弹簧振子的位移－时间图象
课件展示
思考：从此图象可以猜想弹簧振子的 运动随时间的变化规律
三、简谐运动及其图象
１、定义：若质点的位移与时间的关 系遵从正弦或余弦函数变化的规律， 这种运动就叫做简谐运动 ２、振动方程：x=Asin(ωt+Φ ) 3、简谐运动是一种非匀变速运动

想一想
一个完整的全振动过程，有什 么显著的特点？
在一次全振动过程中，一定是
振子连续两次以相同速度通过同一
点所经历的过程。（强调方向性）
2021
33
周期的可能影响因素
弹 簧 振 子 的 再 研 究
2021
34
周期的可能影响因素
弹
簧
振
如何测时间？
子 的
在什么位置测时间？
再
研
结论：周期大小与
究
振幅无关！
2021
35
看一看 两个振子的运动快慢有何不同？
2021
36
2、周期和频率
1)、描述振动快慢的物理量 2)、周期T：做简谐运动的物体完成一次全振
动所需的时间，单位：s。
3)、频率f：单位时间内完成的全振动 的次数，单位：Hz。
4)、周期和频率之间的关系：
f=1/T
5)、周期越小，频率越大，运动越快。
D．O至B位移为负、速度为负
2021
26
简谐运动的特点：
1、简谐振动是最简单、最基本的运动，简谐振 动是理想化的振动。
2、加速度与位移方向相反，总是指向平衡位置 。
3、简谐运动是一种理想化的运动，振动过程中 无阻力，所以振动系统机械能守恒。
4、简谐运动是一种非匀变速运动。 5、位移随时间变化关系图是正弦或余弦曲线.
1位移大小相等方向相反2速度大小相等方向可能相同也可能相反3加速度大小相等方向相反4从平衡位置到达这两个或从这两个点直接到达平衡位置的时间相等对称关系2021471从图像中可直接读出在不同时刻的位移值从而知道位移x随时间变化的情况2可以确定振幅3可以确定振动的周期和频率4可以用作曲线上某点的切线的办法确定各时刻的速度大小和方向5由于简谐运动的加速度和位移大小成正比方向相反可以根据图像上各时刻的位移变化情况确定质点加速度的变化情况202148202149如果两个摆球振动的步调一致称为同相

2.2
简谐运动的描述
目录
CONTENTS
1
简谐运动的表达式
2
描述简谐运动的物理量
3
简谐运动的周期性和对称性
4
简谐运动振幅与路程的关系
有些物体的振动可以近似为简谐运
动，做简谐运动的物体在一个位置附近
不断地重复同样的运动。如何描述简谐
运动的这种独特性呢？
知识回顾：
简谐运动的位移图像是一条正弦曲线。
全振动的特点：①位移和速度都会到初状态 ②路程等于4A
②周期：做简谐运动的物体完成一次全振动所需要的时间，用T表示，
单位：s.
③ 频率：单位时间内完成全振动的次数，用f表示，单位：Hz.
周期T与频率f的关系是T＝
知道即可：弹簧振子的周期由哪些因素决定?
周期公式： T 2
m
k
弹簧振子周期（固有周期）和频率由振动系统本身的因素决定（振子的质量m和弹
②若△ = 2 − 1＜0，振动2的相位比1落后△ 。
4.同相与反相：
（1）同相：相位差为零



△ = 2( = 0，1，2， … )


（2）反相：相位差为
△ = (2 + 1)( = 0，1，2， … )

A与B同相
A与C反相
A与D异相
相位差90°
＝（ ＋ ）
一、简谐运动的表达式
相位
x A sin(t )
振幅
圆频率
初相位
二、描述简谐运动的物理量
＝（ ＋ ）
1.振幅：（1）定义：振动物体离开平衡位置的最大距离。
振幅
O
振幅
（2）物理意义：振幅是描述振动强弱的物理量。

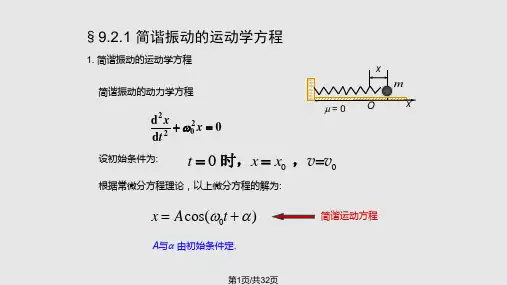
x −t 图
x = A cos ωt
x
A
t
v−t 图
v = − Aω sin ω t
= Aω cos(ω t +
Aω v
t
π
2 )
2
a −t图
a = − Aω 2 cos ω t
Aω
a
t
= Aω 2 cos(ωt + π )
2 描述简谐振动的特征量 (1)振幅 A 频率、 (2)周期、频率、圆频率 弹簧振子 ω = 单 摆
(2)按题意 (2)按题意 t=0 时 m O x
x0=0，v0>0 =0，
X
x0=Acosϕ0=0 , cosϕ0=0 ϕ0=π/2 ,3π/2 =Acosϕ cosϕ ,3π v0=-Aωsinϕ>0 , sin ϕ0 <0, 取ϕ0=3π/2 sinϕ =3π ∴ x=9.8×10-2cos(10t+3π/2) m x=9.8× cos(10t+3π
π
a1 > 0,则
7 11 ω ⋅1+ = π或 π 6 6 6
π
cos(ω⋅1+ϕ0 ) < 0
7 ω ⋅1+ = π 6 6
π
ω = π = 3.14s
−1
31.4 ∴ A= = =10cm ω 3.14
vm
故振动方程为 x =10cos(πt + 方法2 用旋转矢量法辅助求解。 方法2： 用旋转矢量法辅助求解。
ϕ+
π
2
ω
v
31.4 A= = =10cm ω 3.14
o
x =10cos(πt +
π
6

在-π到π之间取值：
22
3
取哪一个值要看初始条件，由于：
v A si n t ()
所以： v0Asin
由于t=0时，质点向正 x 方向运动，所以 v0>0
因此，应取：
3
于是，此简谐振动的表达式： x0.1c2ots() (S)I
3
利用旋转矢量法求解很直观，
根据初始条件就可画出如图所 示的振幅矢量的初始位置，从 而得到：
周期T: Period A co t s ) A ( co ( t T s ) []
A co ts (2 )
T2 T2/
频率ν： 1 T 2
Phase 描述运动状态的量
(3)初相位： t
φ为初相位，Initial Phase 11
5、位移、速度和加速度的相位关系
xA c o ts()
2
2
E 1 kA2
Ek
Ep
2
A o A
弹性力是保守力，总机械能守恒，即总能量不随时间变化。
29
动能的时间平均值:
E kT 10 T1 2k2 A si2(n t)dt
k2ATsi2(n t)dt1k2A
2T0
4
势能的时间平均值:
E PT 10 T1 2k2 A c o 2( st )dt
k2 A T
c
o 2tsdt1k2 A
2 T0
4
30
总能的时间平均值:
EEk
Ep
1kA2 2
1
EK
Ep
E 2
结论：
* 弹簧振子的动能和势能的平均值相等，且 等于总机械能的一半。
* 任一简谐振动总能量与振幅的平方成正比

点旋以转o矢为量原A
的端点在 x轴
上的投影点的
运动为简谐运 动.
第17页/共32页
x Acos(t )
t 0
o
A
x0 x
x0 Acos
点旋以转o矢为量原A
的端点在 x轴
上的投影点的
运动为简谐运 动.
第18页/共32页
t t
o
A
t
x
x Acos(t )
点旋以转o矢为量原A
的端点在 x轴
x1
A1
cos(t
1
)
x A cos(t )
2
2
2
(t 2 ) (t 1)
2
1
第25页/共32页
2 1
0同步 x
超前
π 反相 为其它 落后
x
x
o
to
o
t
t
第26页/共32页
例 一质量为0.01 kg的物体作简谐运动，其振幅 为0.08 m，周期为4 s，起始时刻物体在x=0.04 m 处，向ox轴负方向运动（如图）.试求 （1）t=1.0 s时，物体所处的位置和所受的力；
2
0.04 π)
3
m
t 1.0 s 代入上式得
x 0.069 m
F kx m 2 x 1.70103 N
A π 3
0.08 0.04 o 0.04 0.08
x/m
第28页/共32页
（2）由起始位置运动到x = -0.04 m处所需要的最短时间.
法一 设由起始位置运动到x= -0.04 m处所需要的最短 时间为t
A cos(t π)
2
o
A
a A 2 cos(t )

简谐振动
1
简谐运动的基本概念 1.定义
物体在受到跟偏离平衡位置的位移大小成正比，并且总 指向平衡位置的回复力的作用下的振动，叫简谐运动。 表达式为：F= -kx
（1）简谐运动的位移必须是指偏离平衡位置的位移。也 就是说，在研究简谐运动时所说的位移的起点都必须在 平衡位置处。
（2）回复力是一种效果力。是振动物体在沿振动方向 上所受的合力。
振 幅
f
微波炉、打夯机、跳板跳水、打秋千…
0 f′
⑵防止共振的有：机床底座、航海、 军队过桥、高层建筑、火车车厢…
共振曲线
10
gk005.2008年高考江苏卷12B. (3) 12.B⑶（选修模块3—4）描述简谐运动特征的公式 是x＝ Asinωt ．自由下落的篮球经地面反弹后上 升又落下．若不考虑空气阻力及在地面反弹时的能 量损失，此运动不是 （填“是”或“不是”）简谐 运动. 解析： 简谐运动的特征公式为x = Asinωt，其中A是振幅； 自由落体由反弹起来的过程中，回复力始终为重力， 恒定不变，与偏离平衡位置的位移不是成正比的， 不符合简谐运动的规律。
T与摆球质量m、振幅A都无关。其中l为摆长，表示从 悬点到摆球质心的距离，要区分摆长和摆线长。
（3）小球在光滑圆弧上的往复滚动，和单摆完全等同. 只要摆角足够小，这个振动就是简谐运动。 这时周期公式中的l应该是圆弧半径R和小 球半径r的差。
（4）秒摆的周期为2秒
9
三、 受迫振动与共振 1.受迫振动 物体在驱动力(即周期性外力)作用下的振动叫受迫振动.
（3）在水平方向上振动的弹簧振子的回复力是弹簧的 弹力；在竖直方向上振动的弹簧振子的回复力是弹簧 弹力和重力的合力。
8
2. 单摆 （1）单摆振动的回复力是重力的切向分力，不能说成是 重力和拉力的合力。在平衡位置振子所受回复力是零，但 合力是向心力，指向悬点，不为零。

1. 平衡位置 2. 建立坐标 3.受力分析
弹性力 f kx
4.牛顿运动方程
kx
ma
m
d2 dt
x
2
令 k 2 整理得
m
d 2 x 2 x 0 简谐振动动力学方程
dt 2
解微分方程可得
x A cos(t 0 )
简谐振动运动学方程
二、简谐振动的三个特征量
1.振幅 物体离开平衡位置的最大位移的绝对值 A， 由初始条件决定，描述振动的空间范围。
2.周期 振动状态重复一次所需要的时间,描述振 动的快慢.
Acos[(t T ) 0] Acos(t 0)
T 2π T 2π
1
T
物体在单位时间内发生完全振动的次
数，称振动的频率.
2π 称圆频率（角频率）.
k T 2 m 1 k
m
k
2 m
反映了系统的固有特性，分别称为谐振子系统 的固有圆频率、固有周期和固有频率.
圆频率 k 由系统决定，与初始条件无关
m
振幅 反映振动的强弱，由初始条件决定.
由
x Acos t 0 v A sin t 0
x0 Acos0
t=0时 v0 A sin0 可得
A
x02
v02
2
初相位 0 已知初始振动状态，用旋转矢量确定
x0<0 v0<0
x0=0 v0<0
x0>0 v0<0
例6 某简谐振动的振动曲线如图，写出振动方程。 x(cm)
O
t(s)
-1
1
-2
解： 设振动方程为 x A cos(t 0 )
则由振动曲线： A=2 cm
xA

解：方法1
31.4
15.7
设振动方程为
0
x Acos(t 0 ) 15.7
31.4
1
t(s)
v0 A sin0 15.7cms 1 a0 2 Acos0 0
A vm 31.4cms 1
sin 0
v0
A
15.7 31.4
1 2
0
6
或
5 6
a0
0,则cos0
0
0
6
t 1 v 15.7cms 1 sin( 1 ) v v 1
两振动步调相反,称反相
0
2 超前于1 或 1滞后于 2
相位差反映了两个振动不同程度的参差错落
谐振动的位移、速度、加速度之间的位相关系
x Acos( t 0 )
v
A
sin(
t
0
)
vm
cos(
t
0
2
)
a A 2 cos( t 0 ) am cos( t 0 )
x.v.a. x
衡位置的运动。
• 平衡位置：质点在某位置所受的力（或沿 运动方向受的力）等于0，则此位置称为平 衡位置。
•线性回复力：若作用于质点的力总与质点相对于平 衡位置的位移（线位移或角位移）成正比，且指向 平衡位置，则称此作用力为线性回复力。
若以平衡位置为原点，以X表示质点相对于平衡
位置的位移，则
f kx
3
a 0.12 2 cos( 0.5 ) 0.103
3
(3) 当x = -0.06m时，该时刻设为t1,得 cos(t ) 1
13
2
t 2 , 4
133 3
因该时刻速度为负，应舍去