下载文档原格式
第5课时分数连除和乘除混合运算〖教学内容〗教科书第50页例6和相关练习。
〖教学目标〗1.结合具体的生活情境，使学生经历探索分数连除和乘除混合运算的计算方法的过程。
2.掌握分数连除和乘除混合运算的方法，能正确解答分数连除和乘除混合运算的相关问题。
〖教学重、难点〗重点：掌握分数连除和乘除混合运算的计算方法。
难点：能运用分数连除和乘除混合运算解决稍复杂的分数问题。
〖教学过程〗一、复习导入1.口算。
2/7÷1/2＝ 4×5/8＝4/9÷6＝ 5/9×3/10＝提问：你在口算时，运用了哪些计算方法?引导学生回答：计算分数乘法时，用分子相乘的积作分子，分母相乘的积作分母，能约分的可以先约分，再相乘；计算分数除法时，用被除数乘除数的倒数。
2.我们已经学习了分数乘除法的计算方法，并会用分数乘除法解决一些简单的实际问题，同学们愿意进一步探究分数乘除法的知识吗?（愿意）今天我们就来学习分数连除和乘除混合运算。
板书课题：分数连除和乘除混合运算。
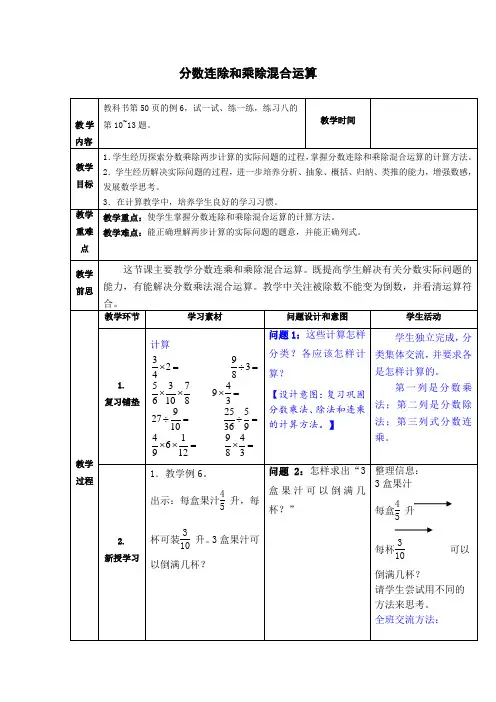
二、探究新知（一）教学例61.理解题意，寻找数学信息。
（1）请同学们读题，理解题意。
（2）提问：从题目中你了解了哪些数学信息?这些信息之间有什么关系?引导学生回答：从题目中我们知道了每盒果汁4/5升，每杯可盛3/10升，要求3盒果汁可以倒满几杯。
这三个信息之间的关系是：3盒果汁可以倒的杯数等于1盒果汁所能倒的杯数的3倍。
（3）追问：要解决“3盒果汁可以倒满几杯”这个问题时，首先要解决什么问题?①学生独立思考后讨论交流。
②反馈汇报。
汇报预测：生1：先算3盒果汁一共有多少升。
生2：先算1盒果汁可以倒几杯。
……2.列出算式，解决问题。
（1）讨论解题方法。
引导：刚才同学们已经知道要求3盒果汁可以倒满几杯，先要求出3盒果汁一共有多少升，或先求出1盒果汁可以倒几杯，那么求出了这两个问题以后，再继续算什么呢?先想一想，再与同桌交流。
学生先独立思考，再在小组里交流自己的解题思路。
分数连除、乘除混合运算教学设计分数连除、乘除混合运算教学设计新龙中心学校曾学杰教学内容：教科书第63页例6及相应的练习教学目标：1.结合具体情境使学生经历探索分数乘除混合运算的过程。
2.帮助学生分析两步计算的应用题的数量关系，能正确解答，提高解题能力。
3.培养学生良好的学习习惯，提高计算能力。
教学重点：让学生能正确灵活地计算分数连除和分数乘除的混合运算。
教学难点：连除和乘除混合运算计算时的转化方法。
教学过程：一、课前练习1、1/5÷3= 6÷3/5= 5/9÷10/21= 7/2×5/6×3/14=2、列式计算（1）每盒果汁4/5升，每杯可装果汁3/10升，一盒果汁能装多少杯？（2）每盒果汁4/5升，有3盒果汁，一共有多少升果汁？二、新授1、出示例6中的三个条件，引导理解题目意思。
（1）读题理解题目意思。
（2）从题目中我们可以知道哪些信息？这些信息之间有什么关系？通过信息的组合，我们又可以获得什么新的信息？2、讨论解决问题的策略。
（1）添加要解决的问题：3盒果汁可以倒多少杯？（2）怎么解决这个问题呢？自己先想一想，看能不能把结果算出来。
（3）交流：你是怎么想的？先算的是什么？①如果先求3盒一共有多少升，怎么想？怎么算？板书：4/5×3 = 12/5（升）12/5 ÷3/10 =8（杯）②如果先求一盒能装几杯呢？板书：4/5÷3/10 = 8/3（杯）8/3×3=8（杯）3、这题如果列综合算式怎么列？（1）各自尝试列式。
（2）指名汇报，根据学生的汇报板书：4/5×3÷3/10 4/5÷3/10 ×3让学生在书上完成计算，并指名板演。
4、教学“试一试”。
（1）出示：5/8 ÷3/4 ÷5/7 ，这题是分数连除，怎么算？（2）学生在书上独立计算后讨论算法师板书计算过程。
分数除法的简单运用，分数连除和乘除混合运算、整理与练习一、本周学习目标：1、掌握分数连除和乘除混合运算的计算方法，能正确进行计算。
2、能够正确解答分数连除和乘除混合运算相关的实际问题。
3、能列方程解答“已知一个数的几分之几是多少，求这个数”等类型的简单实际问题。
4、使学生在探索解决问题时，进一步提高能力，感受数学知识在生活中的应用，提高学好数学的自信心。
二、考点分析：1、在分数连除或分数乘除混合运算中，遇到除以一个数时，只要乘这个数的倒数就可以了。
2、在解答分数除法应用题时要找准单位“1”的量，而简单的分数除法应用题就是要求单位“1”的量。
3、分数除法应用题的数量关系式是： 单位“1” ×分率 = 分率对应的量在具体解答时，用方程做，设单位“1”的量为ⅹ。
4、解答分数除法应用题时，可以借助于线段图来分析数量关系。
在画线段图时，先画单位“1”的量。
三、典型例题例1、（重点展示）计算。
（1）53÷ 6÷ 151 （2）59 × 32÷ 3518分析与解：计算过程中先把除以一个数改为乘这个数的倒数，再按乘法计算法则进行计算。
（1）= 53 × 61× 15 = 23（2）59 × 32÷ 3518 = 59 × 32× 1835 = 37 点评：也许有人会说，不也可以按照计算顺序依次计算吗？是的，可以！但是再想一下，是一下子计算方便呢？还是分步计算方便？当然是一下子转化为连乘计算方便。
例2、（误点诊所）计算15 ÷259× 54 错误解法：15 ÷ 259× 54 = 15 × 925× 45 = 361875分析与解：和例题1一样先转化为连乘的算式，再计算。
正确解答：15 ÷259× 54 = 15 × 925× 54 = 3100点评：在计算过程中除以一个数，只要转化为乘这个数的倒数，而乘一个数是不要变化的。
5 分数连除和乘除混合运算人非圣贤，孰能无过？过而能改，善莫大焉。
《左传》江缘学校 陈思梅内 容1.脱式计算。
225÷15×9 360÷20×5 3×49÷7 4×15÷202.阅读教材第50页例6。
要求3盒果汁可以倒满几杯,可以先求3盒一共有多少升,列式是( ),结果是( ),再求3盒果汁可以倒满几杯,列式是( )。
也可以先求每盒果汁可以倒满几杯,列式是( ),结果是( ),再求3盒果汁可以倒满几杯,列式是( )。
3.列综合算式分别是( )和( )。
4.计算分数乘除混合运算,先把除法转化为( )后再进行计算。
5.分数的乘除混合运算顺序和整数的相同,按从( )到( )依次计算;分数的混合计算也可以先把除法转化为( ),再应用分数的连乘依次计算。
6.预习完之后,你的困惑是什么?有哪些地方不明白?7.脱式计算。
÷÷ ×÷ 4×÷8.用3千克毛线织手套,每副手套需要毛线千克。
已经织了手套总数的。
已经织了多少副手套?温馨知识准备:整数乘除混合运算、分数乘除法。
提示1.135902132.×3÷÷×33.×3÷÷×34.乘法5.左右乘法6.略7. 8.3÷×=24(副)【素材积累】宋庆龄自1913年开始追随孙中山，致力于中国革命事业，谋求中华民族独立解放。
摘近70年的漫长岁月里，经过护法运动(1917年)、国民大革命(1924—1927年)、国共对立十年(1927—1937年)、抗日战争(1937—1945年)、解放战争(1945—1949年)，她始终忠贞不渝地坚持孙中山的革命主张，坚定地和中国人民站摘一起，为祖国的繁荣富强和人民生活的美满幸福而殚精竭虑，英勇奋斗，摘中国现代历史上，谱写了光辉的篇章。
分数连除和乘除混合运算【知识点一】分数连除和乘除混合运算【例题1】每盒果汁54升，每杯可盛103升。
3盒果汁可以倒满几杯?【例题2】（ ）（ ）＝（ ）（ ）（ ）（ ）（ ）（ ）＝⨯⨯÷÷734385知识归钠：计算分数连除和乘除混合运算时，只要把其中的除以一个数转化为乘这个数的倒数，再按分数连乘的计算法则计算。
1.蛇的冬眠时间约是180天，熊的冬眠时间是蛇的32，又是青蛙的54。
青蛙的冬眠时间约是多少天?2.一辆汽车43小时行36千米，照这样计算，从甲地到乙地要行23小时。
甲、乙两地相距多少千米?3.有6台同样的织布机，411小时共织布154米，平均每台织布机每小时织布多少米?【典型例题】一、找准单位“1”，看清等量关系【例题1】已知甲数的43等于乙数的65，甲数是80，则乙数是多少?1.牧场有1500匹马，牛的数量是马的56，又是羊的23。
羊有多少只?【例题2】计算：5425915⨯÷ 15141085÷÷ 25427310÷⨯ 415538⨯÷【例题3】小明和小红都养了一些金鱼，小明把自已金鱼条数的51送给小红后，两人的金鱼条数同样多。
已知小明原来的金鱼比小红多8条，小红和小明原来各有金鱼多少条?2.李芳和赵敏都是集邮爱好者，李芳比赵敏多集邮24枚，李芳把自己邮票的61给赵敏后，两人的邮票数就同样多。
两人原来各有多少枚邮票?3.小云和小乐一共有28本故事书，小云把自己故事书的81借给小乐，两人的故事书就同样多。
两人原来各有多少本故事书?【基础巩固提优】 1.填一填，算一算。
=÷÷1665158( )×( )×( )=( ) 74103218÷⨯=( )×( )×( )=( ) =⨯÷1511121195( )×( )×( )=( ) 2.计算下列各题。
