数与运算(四则运算及运算定律)

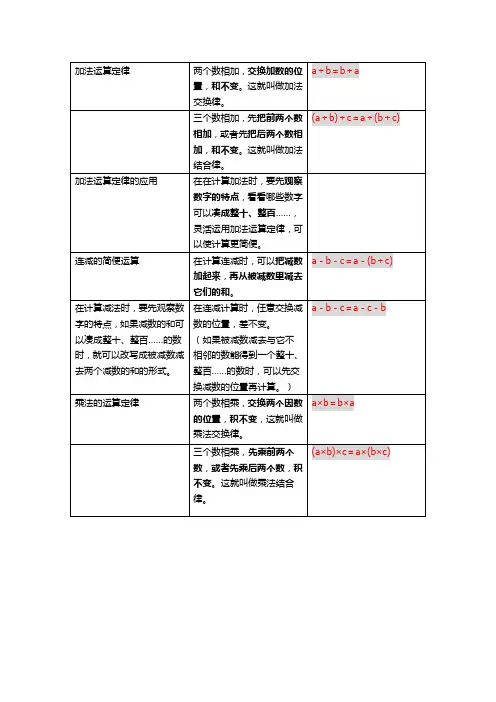
完整版)四则运算和运算定律知识点四则运算和运算定律是数学中的基础知识点。

首先，四则运算包括加法、减法、乘法和除法，没有括号的算式中，单独的加减法或乘除法按顺序从左往右计算，有混合运算的先算乘除法再算加减法。

如果有括号，要先算括号里面的，再算括号外面的，括号的计算顺序为小→中→大，括号里面的运算遵循以上的计算顺序。

其次，运算定律包括加法交换律、加法结合律、乘法交换律、乘法结合律和乘法分配律。

这些定律可以简化计算，例如交换加数位置不影响和的大小，三个数相加可以先把前两个数相加或后两个数相加，积的顺序也可以交换，两个数的和与一个数相乘可以先分别相乘再相加，两个数的差与一个数相乘可以先分别相乘再相减。

此外，还有连减定律和连除定律，也可以简化计算。

最后，我们可以通过简便计算来练四则运算和运算定律的应用，例如常见乘法计算、加法交换律、加法结合律和乘法交换律的简算例题。

掌握好这些知识点，可以帮助我们更快更准确地进行数学计算。

五、乘法结合律的应用：99×125×8可以改写为99×(125×8)，再进行简算得到.六、加法交换律和结合律的应用：65+286+35+714可以改写为(65+35)+(286+714)，再进行简算得到1100.七、乘法交换律和结合律的应用：25×0.125×4×8可以改写为(25×4)×(0.125×8)，再进行简算得到100.八、乘法分配律的应用：1.分解式25×(40+4)可以拆分为25×40+25×4，再进行简算得到1100.2.合并式135×12.3—135×2.3可以拆分为135×(12.3—2.3)，再进行简算得到1350.3.特殊例题1：99×25.6+25.6可以拆分为99×25.6+25.6×1，再进行简算得到2560.4.特殊例题2：45×102可以拆分为45×(100+2)，再进行简算得到4590.5.特殊例题3：99×26可以拆分为(100—1)×26，再进行简算得到2574.6.特殊例题4：35.3×8+35.3×6—4×35.3可以拆分为35.3×(8+6—4)，再进行简算得到353.九、连减的简便运算例子：1.528—6.5—3.5可以拆分为528—(6.5+3.5)，再进行简算得到518.2.528—89—128可以拆分为528—128—89，再进行简算得到311.3.52.8—(40+12.8)可以拆分为52.8—12.8—40，再进行简算得到0.十、连除的简便运算例子：3200÷25÷4可以拆分为3200÷(25×4)，再进行简算得到32.十一、其他简便运算例子：1.256—58+44可以拆分为256+44—58，再进行简算得到242.2.250÷8×4可以拆分为250×4÷8，再进行简算得到125.。

四则运算4、算式有括号，要先算括号里面的，再算括号外面的；括号里面的算式计算顺序遵循以上的计算顺序。

5、加法、减法、乘法和除法统称为四则运算。

关于“0”的运算1、“0”不能做除数；字母表示：a÷0错误2、一个数加上0还得原数；字母表示：a＋0= a3、一个数减去0还得原数；字母表示：a－0= a4、被减数等于减数，差是0；字母表示：a－a = 05、一个数和0相乘，仍得0；字母表示：a×0= 06、0除以任何非0的数，还得0；字母表示：0÷a（a≠0）= 07、0÷0得不到固定的商;5÷0得不到商.运算定律及简便运算：一、加法运算定律：1、加法交换律：两个数相加，交换加数的位置，和不变。

a+b=b+a2、加法结合律：三个数相加，可以先把前两个数相加，再加上第三个数；或者先把后两个数相加，再加上第一个数，和不变。

（a+b）+c=a+(b+c) 加法的这两个定律往往结合起来一起使用。

如：１６５+９３+３５＝９３+（１６５+３５）依据是什么？3、连减的性质：一个数连续减去两个数，等于这个数减去那两个数的和。

a-b-c=a-(b+c)二、乘法运算定律：1、乘法交换律：两个数相乘，交换因数的位置，积不变。

a×b=b×a2、乘法结合律：三个数相乘，可以先把前两个数相乘，再乘以第三个数，也可以先把后两个数相乘，再乘以第一个数，积不变。

（a×b ）× c = a× (b×c )乘法的这两个定律往往结合起来一起使用。

如：１２５×７８×８的简算3、乘法分配律：两个数的和与一个数相乘，可以先把这两个数分别与这两个数相乘，再把积相加。

（a+b）×c=a×c+b×c (a－b)×c＝a×c－b×c乘法分配律的应用：①类型一：（a+b）×c (a－b)×c= a×c＋b×c = a×c－b×c②类型二：a×c＋b×c a×c－b×c=（a+b）×c =(a－b)×c③类型三：a×99＋a a×b－a= a×（99+1） = a×（b－1）④类型四：a×99 a×102= a×（100－1） = a×（100+2）= a×100－a×1 = a×100+a×2三、简便计算1．连加的简便计算：①使用加法结合律（把和是整十、整百、整千、的结合在一起）②个位：1与9，2与8，3与7，4与6，5与5，结合。

四则运算规律总结及其简便运算应用举例第一部分规律总结一、四则运算的运算顺序1、在没有括号的算式里，如果只有加、减法或者只有乘、除法，都要从左往右按顺序计算。

2、在没有括号的算式里，同时有加、减法和乘、除法，要先算乘除法，再算加减法。

3、算式有括号，先算括号里面的，再算括号外面的；括号里面的算式计算顺序遵循以上的计算顺序。

二、关于“0”的运算：1、“0”不能做除数；2、一个娄加上0或者减去0，最终还等于原数3、被减数等于减数，差得04、0乘任何数或0除以任何数，都得0三、运算定律与简便运算（一）加法运算定律：1、两个加数交换位置，和不变这叫做加法交换律。

字母公式：a+b=b+a2、先把前两个数相加，或者先把后两个数相加；和不变，这叫做加法结合律。

字母公式：(a+b)+c=a+(b+c)（二）乘法运算定律1、交换两个因数的位置，积不变，这叫做乘法交换律。

字母公式：a x b=b x a2、先乘前两个数，或者先乘后两个数，积不变，这叫乘法结合律。

字母公式：（a x b）x c=a x(b x c)3、两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加，这员乘法分配律。

字母公式：(a+b) x c=a x c+b x c 或a x (b+c)=a x b+a x c拓展公式：（a-b）x c=a x c- b x c 或a x(b-c)=a x b-a x c（三）减法简便运算：1、一个数连续减去两个数，可以用这个数减去这两个数的和。

用字母表示：a-b-c=a-(b+c)2、一个数连续减去两个数，可以用这个数先减去后一个数再减去前一个数。

用字母表示：a-b-c=a-c-b（四）除法简便运算1、一个数连续除以两个数，可以用这个数除以这两个数的积。

用字母表示：a÷b÷c=a÷(b x c)2、一个数连续除以两个数，可以用这个数先除以后一个数再除以前一个数。

用字母表示：a÷b÷c=a÷c÷b第二部分简便算法应用举例一、加法类型一：利用加法交换律、结合律，观察数的末位特征，将数凑成整数进行简算。

四则运算的运算定律
(一)加法运算定律：
1、两个加数交换位置，和不变，这叫做加法交换律。

字母公式：a+b=b+a
2、先把前两个数相加，或者先把后两个数相加，和不变，这叫做加法结合律。

字母公式：(a+b) +c=a+(b+c)
(二)乘法运算定律：
1、交换两个因数的位置，积不变，这叫做乘法交换律。

字母公式：a×b=b×a
2、先乘前两个数，或者先乘后两个数，积不变，这叫做乘法结合律。

字母公式：(a×b)×c=a×(b×c)
3、两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加，这叫做乘法分配律。

用字母公式：(a+b)×c=a×c+b×c或a×(b+c) =a×b+a×c 拓展：(a-b)×c=a×c-b×c或a×(b-c) =a×b-a×c
(三)减法简便运算：
1、一个数连续减去两个数，可以用这个数减去这两个数的和。

用字母表示：a-b-c=a-(b+c)
2、一个数连续减去两个数，可以用这个数先减去后一个数再减去前一个数。

用字母表示：a-b-c=a—c-b
(四)除法简便运算：
1、一个数连续除以两个数，可以用这个数除以这两个数的积。

用字母表示：a÷b÷c=a÷(b×c)
2、一个数连续除以两个数，可以用这个数先除以后一个数再除以前一个数。

用字母表示：a÷b÷c=a÷c÷b。

四则运算定律概念及公式
四则运算是指加法、减法、乘法和除法这四种基本运算。

四则运算定律是指这四种基本运算中的一些性质和规则。

1.加法定律：
-交换律：对于任意的实数a和b，a+b=b+a。

-结合律：对于任意的实数a、b和c，(a+b)+c=a+(b+c)。

2.减法定律：
-减法与加法的关系：对于任意的实数a、b和c，如果a+b=c，那么c-b=a。

3.乘法定律：
-交换律：对于任意的实数a和b，a*b=b*a。

-结合律：对于任意的实数a、b和c，(a*b)*c=a*(b*c)。

4.除法定律：
-除法与乘法的关系：对于任意的实数a、b和c（其中b和c不为零），如果a*b=c，那么c/b=a。

-倒数：对于任意的非零实数a，存在一个实数b，使得a*b=1，这个b被称为a的倒数，记作1/a。

此外，还有一些其他的四则运算定律：
5.零元素：
-加法的零元素：对于任意的实数a，a+0=a。

-乘法的零元素：对于任意的实数a，a*0=0。

6.乘法的单位元：
-乘法的单位元：对于任意的实数a，a*1=a。

7.分配律：
-左分配律：对于任意的实数a、b和c，a*(b+c)=a*b+a*c。

-右分配律：对于任意的实数a、b和c，(a+b)*c=a*c+b*c。

以上是四则运算的一些基本定律和公式。

在进行四则运算时，这些定律和公式可以帮助我们简化和优化计算过程，提高计算的准确性和效率。

四则运算运算定律性质整理一，四则运算运算定律1.加法结合律: 三个数相加，先把前两个数相加，再加上第三个数，或者先把后两个数相加，再和第一个数相加，他们的和不变，这叫加法结合律。

字母表达式 : ( a + b )+ c = a + ( b + c ) 例子： 456+455+445=456=456+(455+445)=456+900=13562.乘法结合律：三个数相乘，先把前两个数乘，再乘第三个数，或者先把后两个数相乘，再和第一个数相乘 ,它们的积不变，这叫乘法结合律。

字母表达式：（ a xb )xc = a x (b x c ) 例子 : 243x8x125=243x( 8x125)=243x1000=2430003. 加法交换律: 两个数相加，交换加数的位置，它们的和不变，这叫做加法交换律。

字母表达式： a + b= b = a 例子: 123+345=345=1234乘法交换律 : 两个数相乘, 交换因数的位置，他们积不变，这叫做乘法交换律。

字母表达式： a x b = b x a 例子： 1276 x762 =762 x12765. 乘法分配律：两个数的和和一个数相乘，可以把两个加数分别与这个数相乘，再把两个积相加，所得的结果不变，这叫乘法分配律。

字母表达式：（ a + b ） x c= a x c + b x c 例子：( 100+ 125 ) x8 = 8 x100 + 8x 125 =800 +1000 =1800二，四则运算性质1.减法运算性质:一个数连续减去两个数，可以先把两个减数加起来，再从被减数里减去。

字母表达式: a - b - c =a - ( b + c ) 例子: 274 – 23 – 177 =274 - (23 + 177 )=274 - 200 = 742.除法运算性质 :一个数连续除以两个数，可以先把两个除数乘起来 , 再去除被除数。

字母表达式： a ÷ b ÷ c = a ÷ ( b x c ) (b≠0 c≠0) 例子： 2000 ÷8÷125 =2000÷（8 x125 ） = 2000 ÷1000= 23.商不变性质:被除数和除数同时乘或除以一个相同的数，(零除外) ,它们的商不变，这叫做商不变性质. 字母表达式： a ÷ b = ( a ÷x c)÷ ( b ÷x c) ( b ≠ 0) ( c≠0 )例子:1100÷25 = (1100 x4 ) ÷ ( 25x 4) =4400÷100 =44。

10 总复习本单元的复习包括四则运算、观察物体(二)、运算律、小数的意义和性质、三角形、小数的加法和减法、图形的运动(二)、平均数与条形统计图、数学广角——鸡兔同笼这九个单元的内容。

其中，四则运算的意义及其关系，运算律，小数的意义、性质和加、减法运算，图形与运动中的轴对称图形的知识，统计知识中的平均数等是本册教科书的重点内容，回顾与整理时要重点处理。

在内容的具体安排上,本单元既遵循所学知识的顺序,同时又对相关内容进行集中安排。

这样,一方面对新学的知识进行整理和复习，另一方面突出了知识之间的内在联系,便于学生形成知识网络。

本学期学生理解、分析能力，解决问题的能力都有明显的进步，在学习过程中暴露出来的问题也较多。

部分学生做口算题比较容易出错，特别是简单的小数加法和减法口算习题。

对于运算律的应用，以及稍微有难度的简便计算，学生也会出现失误。

个别学生对三角形的分类和特征掌握不牢。

在空间与图形方面，部分学生不能够画出同一物体从不同方向观察所看到的平面图形，不能正确掌握平移的方法等。

这些问题都是本单元复习要突破的难点。

1.在复习前，教师要充分了解学生对本学期知识的掌握情况，如概念的理解水平、对易混淆概念的掌握情况、计算的正确率、普遍容易出错的问题等，从而根据具体情况制定恰当有效的复习计划。

2.重视知识的融会贯通，引导学生学会梳理知识的方法。

复习中应引导学生抓住知识间的联系，将零散的知识点联系起来形成知识网络，将所学知识系统化。

实际教学中，一是可采取抓住核心知识，辐射扩展的方式来复习。

如小数的意义、性质及大小比较，小数点位置移动引起小数大小变化等知识的复习，以小数的意义为基本出发点，围绕位值思想和十进制的概念，将小数的性质、读写法、大小比较，小数点位置移动引起小数大小变化等知识进行系统整理，使学生更好地理解与掌握。

二是可引导学生在不同梳理方式的比较中学会复习。

如在运算律等知识内容复习梳理时，有学生可能以直接写文字的方式梳理，也有学生用表格的方式来梳理等。