数学与统计学院

数学与统计学院副院长述职述廉述学报告尊敬的领导、老师和同事们：大家好！我是数学与统计学院的副院长，今天非常荣幸能够向大家述职述廉述学。

在过去的一年里，我带领全院师生积极投入工作，努力推动学院发展，取得了一些成绩和经验，同时也存在一些不足和问题。

下面将就我个人的工作情况、廉洁自律以及学术研究等方面进行报告，希望能得到大家的认可和建议。

首先，我要向大家汇报一下我过去一年的工作。

作为副院长，我负责协助院长进行学院的日常管理和决策，主要职责包括教学管理、科研管理、人才培养和学院建设等方面。

在教学管理方面，我积极推动课程改革和优化教学资源配置，组织教师进行教学培训，提高教学质量。

在科研管理方面，我注重鼓励和支持教师进行科研项目申报和学术交流，帮助他们提高研究水平和学术能力。

在人才培养方面，我致力于加强学生的科研训练和创新能力培养，组织学生参与科研项目和竞赛活动，提高他们的综合素质和竞争力。

在学院建设方面，我积极落实学院发展规划，推动学院内外合作，争取更多的资源和支持，促进学院的可持续发展。

然而，我也意识到在工作中存在一些不足和问题。

首先，我在教学管理方面还需要进一步提高，加强与教师的沟通和协调，更好地满足学生的学习需求。

其次，我需要更加注重科研管理和项目申报工作，提高教师的科研积极性和创新能力。

同时，我也要加强与其他学院和单位的合作，扩大学院的影响力和资源优势。

最后，我还需重视学生的培养工作，更好地引导学生发展兴趣和特长，提高他们的综合素质和就业竞争力。

在廉洁自律方面，我始终严格要求自己，遵守学校和学院的规章制度，不违反纪律要求。

我坚决抵制各种形式的腐败和贪污行为，保持廉洁自律，充分履行副院长的职责与义务。

我保持与同事们的良好互动和沟通，对学院资源和财务进行科学、规范的管理，确保每一笔开支都合理、透明、有效。

最后，在学术研究方面，我积极参与学术交流和合作，提高个人的研究水平和学术能力。

我发表了若干学术论文，在国内外学术会议上进行了多次学术报告，同时还积极指导学生进行科研项目并取得了一定成果。

全日制应用统计专业学位硕士研究生培养方案代码： 025200 （Applied Statistics)“应用统计硕士”为国务院学位办正式批准设立的专业硕士学位，是在统计学科基础上，为适应我国现代统计事业对应用统计专门人才的迫切需要、完善应用统计人才培养体系、创新应用统计人才培养模式、提高应用统计人才培养质量而特设的硕士专业学位。

应用统计硕士专业学位和学术学位处于同一层次，培养方向各有侧重，其对研究生的培养具有实用性、技能性、实践性强、应用性广的特点，主要面向经济社会产业部门专业需求，培养各行各业特定职业的专业人才。

“应用统计硕士”英文名为“Master of Applied Statistics”,英文缩写为M.A.S.。

本学位的优势在于，即适应我国经济建设对实用型统计和数据分析人才的需求，又充分借鉴了国际上培养专业统计和数据分析人才的先进经验，且与目前国内的职业资格认证制度（调查分析师）互相配合和衔接，从而使得本学位的市场需求广泛，教学内容和手段先进，具有良好的发展前景。

一、领域概况统计学作为涵盖应用统计专业的一级学科，是一门关于用科学方法收集、整理、汇总、描述和分析数据资料，并在此基础上进行推断和决策的科学。

统计学有如下的性质和特点：1、统计学研究的对象是客观现象的数量方面。

随着人类活动各种实践的需要，各个领域都要研究事物的数量方面，以及密切联系数量方面来研究事物的本质。

因此统计的应用越来越广泛。

统计方法已渗透到其他学科领域，成为当前最活跃的学科之一。

2、统计学研究的是群体现象的数量特征与规律性。

客观世界是十分复杂的，但根据其不同的性质加以分类就形成各种群体，在统计学中把所研究的某类客观现象的群体称作总体, 统计研究的最终目的是研究总体的数量特征及其规律性。

3、统计学是一门方法论的科学。

在统计学界对统计学的性质有实质性科学和方法论科学之争。

普遍认为统计学是实用性很强的科学，就统计工作来说，他总是研究实际问题的，统计的方法也是从现实问题中产生的。

一、报考情况分析1.招生目录招生年份：2023年招生专业：070100 数学研究方向：01 代数及其表示02 几何、拓扑与分析03 图论与组合优化04 微分方程理论及其应用05 计算、几何力学与控制拟招生人数：5考试科目：①101 思想政治理论②201 英语一③601 数学分析④847高等代数复试要求及相关说明：笔试科目:综合数学基础知识笔试(含复变函数、实变函数、常微分方程、近世代数、拓扑学)。

面试内容:外语口语听力测试；综合基础知识面试。

2.复试分数线2023年复试分数线：单科（45/45/68/68），总分 347；招生计划：18 人，参加复试 22 人。

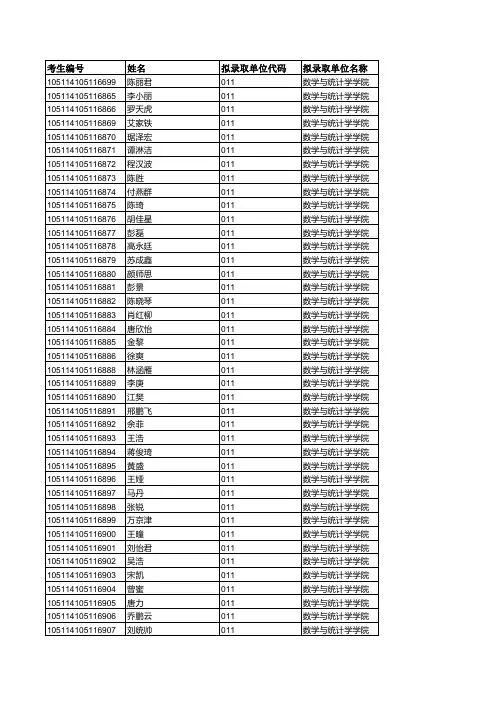
3.录取名单二、考试大纲及参考书目847 高等代数1．考试内容1. 一元多项式理论：最大公因式与因式分解，重因式，不可约多项式，复数域上的不可约多项式，实数域上的不可约多项式，有理系域上的不可约多项式，多元多项式环。

2. 行列式：行列式的定义，行列式的计算及性质，Laplace展开定理。

3. 线性方程组理论：Cramer法则，Gauss消元法，维向量的线性相（无）关性，向量组的秩和矩阵的秩，线性方程组有解的判别，线性方程组解的结构。

4. 矩阵：矩阵的混合运算，方阵的行列式，矩阵的逆，矩阵的分块，初等矩阵，正交矩阵，欧几里得空间。

5. 矩阵的相抵与相似：矩阵的相抵，广义逆矩阵，矩阵的相似，矩阵的特征值和特征向量，矩阵可对角化的条件，实对称矩阵的对角化。

6. 二次型：二次型及其标准形，实二次形的规范形，正定二次型与正定矩阵。

7. 线性空间：线性空间的结构，子空间以及子空间的交与和，子空间的直和，线性空间的同构，商空间。

8. 线性映射：线性映射及其运算，线性映射的核与象，线性映射的矩阵表示，线性变换的特征值与特征向量，线性变换的不变子空间，Hamilton-Cayle定理，线性变换的最小多项式，幂零变换的结构，线性变换的Jordan标准形，线性函数与对偶空间。