数学与计算机科学学院

070102 计算数学计算数学也叫做数值计算方法或数值分析。

主要内容包括代数方程、线性代数方程组、微分方程的数值数值逼近问题，矩阵特征值的求法，最优化计算问题，概率统计计算问题等等，还包括解的存在性、唯一性差分析等理论问题。

我们知道五次及五次以上的代数方程不存在求根公式，因此，要求出五次以上的高次代一般只能求它的近似解，求近似解的方法就是数值分析的方法。

对于一般的超越方程，如对数方程、三角方采用数值分析的办法。

怎样找出比较简洁、误差比较小、花费时间比较少的计算方法是数值分析的主要课题的办法中，常用的办法之一是迭代法，也叫做逐次逼近法。

迭代法的计算是比较简单的，是比较容易进行的以用来求解线性方程组的解。

求方程组的近似解也要选择适当的迭代公式，使得收敛速度快，近似误差小。

在线性代数方程组的解法中，常用的有塞德尔迭代法、共轭斜量法、超松弛迭代法等等。

此外，一些比消去法，如高斯法、追赶法等等，在利用计算机的条件下也可以得到广泛的应用。

在计算方法中，数值逼近本方法。

数值逼近也叫近似代替，就是用简单的函数去代替比较复杂的函数，或者代替不能用解析表达式表值逼近的基本方法是插值法。

初等数学里的三角函数表，对数表中的修正值，就是根据插值法制成的。

在遇到求微分和积分的时候，的函数去近似代替所给的函数，以便容易求到和求积分，也是计算方法的一个主要内容。

微分方程的数值解法。

常微分方程的数值解法由欧拉法、预测校正法等。

偏微分方程的初值问题或边值问题，目前常用的是有限元素法等。

有限差分法的基本思想是用离散的、只含有限个未知数的差分方程去代替连续变量的微分方程求出差分方程的解法作为求偏微分方程的近似解。

有限元素法是近代才发展起来的，它是以变分原理和剖分的方法。

在解决椭圆形方程边值问题上得到了广泛的应用。

目前，有许多人正在研究用有限元素法来解双曲方程。

计算数学的内容十分丰富，它在科学技术中正发挥着越来越大的作用。

排名学校名称等级1 北京大学A+2 浙江大学 A+3 吉林大学A+4 大连理工大学A+5 西安交通大学A北京大学：http:/NewsSpecialDetailsInfo.aspx?SID=4浙江大学：http:/NewsSpecialDetailsInfo.aspx?SID=21847吉林大学：http:/NewsSpecialDetailsInfo.aspx?SID=5506大连理工大学：http:/NewsSpecialDetailsInfo.aspx?SID=4388西安交通大学：http:/NewsSpecialDetailsInfo.aspx?SID=18285有该专业的部分院校分数一览（A+、A、B+、B各选部分代表院校）。

中山大学本科教学大纲Undergraduate Course Syllabus学院（系）：数据科学与计算机学院School (Department)：School of Data and Computer Science课程名称：离散数学基础Course Title：Discrete Mathematics二〇二〇年离散数学教学大纲Course Syllabus: Discreate Mathematics（编写日期：2020 年12 月）(Date: 19/12/2020)一、课程基本说明I. Basic Information二、课程基本内容 II. Course Content（一）课程内容i. Course Content1、逻辑与证明（22学时） Logic and Proofs (22 hours)1.1 命题逻辑的语法和语义(4学时) Propositional Logic (4 hours)命题的概念、命题逻辑联结词和复合命题，命题的真值表和命题运算的优先级，自然语言命题的符号化Propositional Logic, logic operators (negation, conjunction, disjunction, implication, bicondition), compound propositions, truth table, translating sentences into logic expressions1.2 命题公式等值演算(2学时) Logical Equivalences (2 hours)命题之间的关系、逻辑等值和逻辑蕴含，基本等值式，等值演算Logical equivalence, basic laws of logical equivalences, constructing new logical equivalences1.3 命题逻辑的推理理论（2学时）论断模式，论断的有效性及其证明，推理规则，命题逻辑中的基本推理规则（假言推理、假言易位、假言三段论、析取三段论、附加律、化简律、合取律）,构造推理有效性的形式证明方法Argument forms, validity of arguments, inference rules, formal proofs1.4 谓词逻辑的语法和语义 (4学时) Predicates and Quantifiers (4 hours)命题逻辑的局限，个体与谓词、量词、全程量词与存在量词，自由变量与约束变量，谓词公式的真值，带量词的自然语言命题的符号化Limitations of propositional logic, individuals and predicates, quantifiers, the universal quantification and conjunction, the existential quantification and disjunction, free variables and bound variables, logic equivalences involving quantifiers, translating sentences into quantified expressions.1.4 谓词公式等值演算(2学时) Nested Quantifiers (2 hours)谓词公式之间的逻辑蕴含与逻辑等值，带嵌套量词的自然语言命题的符号化，嵌套量词与逻辑等值Understanding statements involving nested quantifiers, the order of quantifiers, translating sentences into logical expressions involving nested quantifiers, logical equivalences involving nested quantifiers.1.5谓词逻辑的推理规则和有效推理(4学时) Rules of Inference (4 hours)证明的基本含和证明的形式结构，带量词公式的推理规则（全程量词实例化、全程量词一般化、存在量词实例化、存在量词一般化），证明的构造Arguments, argument forms, validity of arguments, rules of inference for propositional logic (modus ponens, modus tollens, hypothetical syllogism, disjunctive syllogism, addition, simplication, conjunction), using rules of inference to build arguments, rules of inference for quantified statements (universal instantiation, universal generalization, existential instantiation, existential generalization)1.6 数学证明简介(2学时) Introduction to Proofs (2 hours)数学证明的相关术语、直接证明、通过逆反命题证明、反证法、证明中常见的错误Terminology of proofs, direct proofs, proof by contraposition, proof by contradiction, mistakes in proofs1.7 数学证明方法与策略初步(2学时) Proof Methods and Strategy (2 hours)穷举法、分情况证明、存在命题的证明、证明策略（前向与后向推理）Exhaustive proof, proof by cases, existence proofs, proof strategies (forward and backward reasoning)2、集合、函数和关系（18学时）Sets, Functions and Relations(18 hours)2.1 集合及其运算(3学时) Sets (3 hours)集合与元素、集合的表示、集合相等、文氏图、子集、幂集、笛卡尔积Set and its elements, set representations, set identities, Venn diagrams, subsets, power sets, Cartesian products.集合基本运算（并、交、补）、广义并与广义交、集合基本恒等式Unions, intersections, differences, complements, generalized unions and intersections, basic laws for set identities.2.2函数(3学时) Functions (3 hours)函数的定义、域和共域、像和原像、函数相等、单函数与满函数、函数逆与函数复合、函数图像Functions, domains and codomains, images and pre-images, function identity, one-to-one and onto functions, inverse functions and compositions of functions.2.3. 集合的基数（1学时）集合等势、有穷集、无穷集、可数集和不可数集Set equinumerous, finite set, infinite set, countable set, uncountable set.2.4 集合的归纳定义、归纳法和递归（3学时）Inductive sets, inductions and recursions (3 hours)自然数的归纳定义，自然数上的归纳法和递归函数；数学归纳法（第一数学归纳法）及应用举例、强归纳法（第二数学归纳法）及应用举例；集合一般归纳定义模式、结构归纳法和递归函数。

泉州师范学院简介Quanzhou Normal University泉州师范学院坐落在全国首批历史文化名城、著名侨乡、国际花园城市——福建省泉州市，有东海和诗山两个校区，占地1185亩。

东海主校区位于晋江和洛阳江两江交汇处，携江临海，极目古港沧澜；诗山校区南倚高盖名山，北眺鹏峰胜景。

泉州师范学院前身为创办于1958年的泉州大学师范学院，此后历经更名、停办、复办等发展历程。

1998年泉州师专、泉州教育学院、泉州师范学校合并为新泉州师专，2000年3月经国家教育部批准正式升格为泉州师范学院，系福建省第一所新建地方性省属本科高校。

2001年10月原南安师范学校并入泉州师范学院。

2004年学校顺利通过教育部本科教学工作水平评估，现在已成为一所立足泉州、面向福建、辐射全国，集普通教育和特殊教育为一身，融师范教育与非师范教育为一体的新型现代化大学。

在50多年的办学进程中，向社会输送了8万余名专门人才，为地方教育事业、经济建设和社会发展作出了重要贡献。

学校现有文学与传播学院、政治与社会发展学院、物理与信息学院、数学与计算机学院、外国语学院、资源与环境科学学院、化学与生命科学学院、陈守仁工商信息学院、教育科学学院、音乐与舞蹈学院、美术与设计学院、体育学院、应用科技学院、继续教育学院、软件学院等14个二级学院和1个思政教研部，全日制在校生13880人；另有1个校企合作软件学院。

全日制本科专业44个，涵盖文、史、理、工、经、法、管、教育等八大学科门类。

拥有国家级人才培养模式实验区1个，福建省重点学科4个、省级精品课程19门、省级实验教学示范中心3个、省级人才培养模式创新实验区项目3个、省级特色专业6个、省级教学团队3个。

学校在50多年的办学实践中秉承“以教学工作为中心，以本科教学为主体，以教学改革为动力，以提高教学水平为目标”的办学指导思想，始终坚持“厚基础、宽口径、能创新、适应性强”的人才培养观，以科学发展观为指导，以质量求生存，以特色促发展，努力把学校办成开放型、有特色、高水平地方大学。

西南民族大学计算机科学与技术学院专业介绍计算机科学与技术学院计算机科学与技术学院拥有计算机科学与技术、软件工程、信息与计算科学、数学与应用数学、信息管理与信息系统5个本科专业；学院有8个教研室，系统实验室（国家民委重点）、计算机应用技术实验室和教学实验中心共3个综合实验室，1个计算机应用技术研究所。

现有来自全国各地的本科大学生1530余人，教职工80余人。

专职教师中，具有教授、副教授职称的26名，硕博研究生比例为70.00%，35岁及以下青年教师中研究生比例为96.91%。

实验室面积3500m2，设备总值1450余万元。

近年来，教师共发表论文200余篇，先后有多名教师荣获省部级科技进步和教学成果奖，现有在研项目30余项。

近三年，共有三十余名学生在全国大学生数学建模竞赛中荣获国家和省级奖励。

计算机科学与技术培养目标：本专业培养具有良好的科学素养，能系统地掌握计算机科学与技术的基本理论、基本知识和基本技能的高级专门人才。

主干课程：高等数学、离散数学、数据库原理及应用、数据结构、计算机组成原理、操作系统、汇编语言、计算机网络、现代网络技术、编译原理、计算机图形学、人工智能、单片机技术等。

学制学位：本科、学制四年，毕业合格者授予工学学士学位。

软件工程培养目标：本专业培养适应国民经济信息化建设和发展的需要，系统地掌握软件工程专业基本理论、基本知识及基本技能与方法；具有很强的工程实践能力；具有运用先进的工程化方法技术和工具从事软件分析、设计、开发、维护等工作的能力；具有团队协作能力、技术创新能力和市场开拓能力的实用型、复合型软件工程技术人才。

主干课程：面向对象程序设计（C++/Java）、离散数学、数据结构与算法、计算机组织与结构、数据库概论、操作系统、软件工程导论、软件开发过程、软件项目管理、软件需求工程、软件构件技术、软件过程模型、软件质量保证与软件测试、大型数据库系统开发、J2EE架构与程序设计等。

学制学位：本科、学制四年，毕业合格者授予工学学士学位。

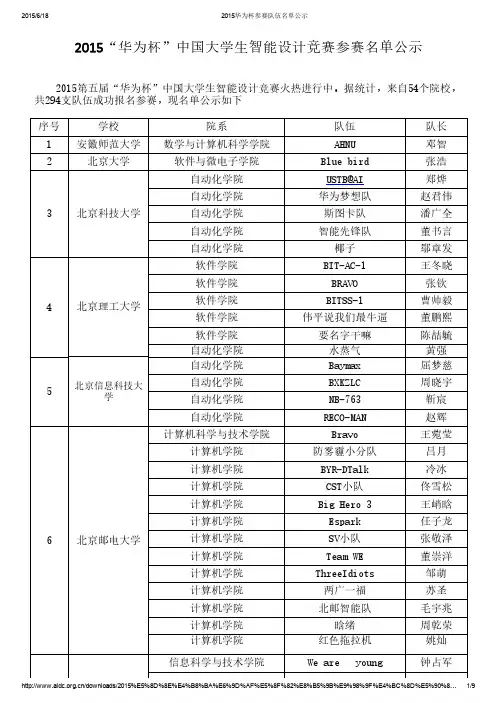
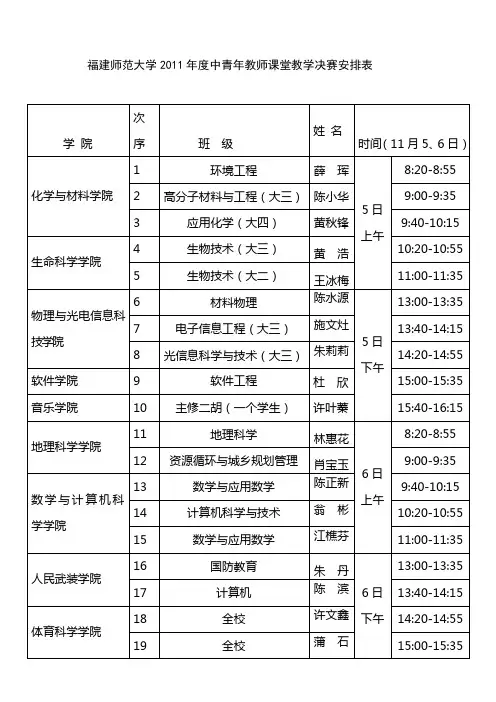
福建师范大学2011年度中青年教师课堂教学决赛安排表
2010、2011年新进教师名单
经济学院：陈丰、王珍珍、唐杰、陈洪昭
文学院：周云龙、林强、肖满省、叶黛莹、王炳中、王申、谢刚
传播学院：彭艳戎、林升梁、彭飙
社会历史学院：林泽斐
公共管理学院：张廷君
外国语学院：吕颖、郑奕、林静
音乐学院：吴凡、潘达、杨明玉、许琛、宋方方
美术学院：潘颖、陈艳、胡新地
体育科学学院：许建政、王韶玉
数学与计算机科学学院：李德梅、陈兰香、林贤祖、张世芳、唐嘉
物理与光电信息科技学院：王哲哲、王丽丽
化学与材料学院：黄秋锋、戴宏、蔡开聪、黄静
地理科学学院：吴勇、张金凤、林啸、朱芸、雷国良、司友涛、林成芳生命科学学院：郑永标
软件学院：倪友聪、杜欣
海外教育学院：谢婧怡、陈海峰、林琳琳、黄燕萍。

1.中山大学（985）广东省广州软件工程：867专业基础（数据结构）620)软件学院院系：100 本专：100 推免：60 专业：40621)（1）101思想政治理论（2）204英语二（3）302数学二（4）867专业基础（数据结构）复试专业课：F62 01计算机综合考试①《离散数学》，耿素云、屈婉玲，高等教育出版社，1998。

②《C程序设计》第二版，谭浩强编，清华大学出版社，1999。

计算机技术：（408）综合350)信息科学与技术学院院系：287 专硕：143 推免：100 一般：43 (470)中山大学-卡内基梅隆大学联合工程学院（922）数据结构与计算机原理本专：40分数线：300；270；2702.华南理工大学（985）广东省广州计算机技术：（831）计算机专业综合(数据结构、操作系统)008)计算机科学与工程学院院系：133 专业招生人数:55① 101思想政治理论② 204英语1③302数学1④831计算机专业综合(数据结构、操作系统) 复试笔试科目：902上机能力测试:数据库复试科目参考书：《数据库系统概论》(第三版)王能斌著，,电子工业出版社；《数据库系统概念》(第四版)中文版，杨冬青、唐世渭等编译，机械工业出版社；《数据库系统教程》王能斌著，电子工业出版社软件工程：（408）综合(023)软件学院院系：74推免：373.暨南大学（211）广东省软件工程和计算机技术：（830）数据结构(010)信息科学技术学院院系：110 推免：20 软件工程专业：10①101思想政治理论②204英语二③302数学二④830数据结构830数据结构1．严蔚敏、吴伟民, 数据结构（C语言版）,清华大学出版社出版2．严蔚敏, 吴伟民,《数据结构习题解析》,清华大学出版社出版复试科目：C语言程序设计加试科目：①离散数学②计算机基础！！华南师范大学广东省软件工程：（918)计算机综合考试（操作系统、程序设计）(019)计算机学院院系：62 推免：164.华东师范大学（985）上海市085211 数据结构（含c语言）计算机技术1.上机考试：主要考查学生运用计算机编程解决问题的能力，上机语言为C或C++。

数学与计算机科学学院师资队伍信息2013-10-19李星，男，汉族， 1964 年生，博士（德国），宁夏大学教授 , 曾任宁夏大学副校长，现任宁夏师范学院院长；上海交通大学兼职教授、博士生导师，《中国数学文摘》副主编，宁夏大学学报（自然科学版）主编（中文核心期刊），第十届全国政协委员，第五届、第六届中国科协委员，第九届全国青联委员，第八届、第九届中国数学会理事，第七届宁夏青联副主席，第五届、第六届宁夏回族自治区科协副主席；第七届、第八届宁夏政协委员；第十届宁夏人大代表；首届宁夏高级专家联合会副会长；中国数学会副理事长；宁夏数学会理事长；宁夏力学会理事长；宁夏回族自治区重点学科“应用数学”专业的学科带头人； 211 重点学科“数学力学及工程技术科学计算”的学科带头人。

入选教育部“高层次创造性人才计划”获青年教师奖，首届国家“百千万人才工程”一、二层次人选 , 中央直接联系专家。

马应虎，男，回族，1958年7月出生，宁夏海原县人，中共党员。

1982年1月毕业于宁夏大学数学系，理学学士，2000年评聘为教授，曾任固原师专数学系副主任、主任、教务处处长、校长助理，2005年8月任宁夏师范学院党委委员、副院长，现任宁夏大学副校长。

教育部“曾宪梓教育基金会高等师范院校教师奖”三等奖获得者；“数学与应用数学”区级教学团队负责人；“数学与应用数学”区级特色专业负责人；宁夏师范学院“基础数学”校级重点学科学科带头人；区级精品课程《高等代数》的主要完成人，主要担任“高等代数”、“近世代数”等课程的教学工作。

2007年主持完成区级教改项目“普通高校兼办高职教育人才培养模式创新研究”；2008年主持完成区级教改项目“宁夏高校专业建设发展趋势研究”；2009年主持完成区社科项目“教育公平与优质教育资源配置”，参与完成2个省部级教学科研项目，主持完成3项校级教学科研项目。

近五年来发表《发挥师范教育在教师教育中的主体作用》等研究论文8篇；出版《近世代数基础》等专著4部，主持完成的”近世代数教学改革研究“获2011学年度校级优秀教学成果一等奖；2010年研究报告《西北地区中小学教师流动问题研究》获第四届全国教育科学研究优秀成果三等奖（主要完成人）；2010年研究报告《宁南山区农村小学教师流动与教育公平研究》获宁夏首届优秀教育研究成果一等奖(主要完成人)；2010年著作《高等职业教育的改革与发展》获宁夏首届优秀教育研究成果二等奖。