13： 第六章 勒让德多项式

勒让德多项式[编辑]维基百科，自由的百科全书伴随勒让德多项式有时也简称为“勒让德多项式”。

数学上，勒让德函数指以下勒让德微分方程的解：为求解方便一般也写成如下施图姆-刘维尔形式（Sturm-Liouville form）:上述方程及其解函数因法国数学家阿德里安-马里·勒让德而得名。

勒让德方程是物理学和其他技术领域常常遇到的一类常微分方程。

当试图在球坐标中求解三维拉普拉斯方程（或相关的其他偏微分方程）时，问题便会归结为勒让德方程的求解。

勒让德方程的解可写成标准的幂级数形式。

当方程满足|x| < 1 时，可得到有界解（即解级数收敛）。

并且当n 为非负整数，即n = 0, 1, 2,... 时，在x = ±1 点亦有有界解。

这种情况下，随n 值变化方程的解相应变化，构成一组由正交多项式组成的多项式序列，这组多项式称为勒让德多项式（Legendre polynomials）。

勒让德多项式Pn(x)是n 阶多项式，可用罗德里格公式表示为：目录 [隐藏]1 正交性2 部分实例3 在物理学中的应用4 其他性质4.1 奇偶性4.2 递推关系5 移位勒让德多项式6 分数阶勒让德多项式7 参见8 外部链接9 参考文献正交性[编辑]勒让德多项式的一个重要性质是其在区间−1 ≤x ≤ 1 关于L2内积满足正交性，即：其中δmn 为克罗内克δ记号，当m = n 时为1，否则为0。

事实上，推导勒让德多项式的另一种方法便是关于前述内积空间对多项式{1, x, x2, ...}进行格拉姆-施密特正交化。

之所以具有此正交性是因为如前所述，勒让德微分方程可化为标准的strum-liouville问题：其中本征值λ对应于原方程中的n(n+1)。

部分实例[编辑]下表列出了头11阶（n 从0到10）勒让德多项式的表达式：n12345678910头6阶（n 从0到5）勒让德多项式的曲线如下图所示：在物理学中的应用[编辑]在求解三维空间中的球对称问题，譬如计算点电荷在空间中激发的电势时，常常要用到勒让德多项式作如下形式的级数展开：其中和分别为位置向量和的长度，为两向量的夹角。

第六章 勒让德多项式在这一章，我们将通过在球坐标系中对Laplace 方程进行分离变量，引出§2.6中曾指出过的勒让德方程，并讨论这个方程的解法及解的有关性质。

勒让德方程在区间[1,1]-上的有界解构成了另一类正交函数系－勒让德多项式。

§6.1 勒让德方程的引出现在对球坐标系中的Laplace 方程进行分离变量，在球坐标系中Laplace 方程为2222222111()(sin )0sin sin u u ur r r r r r θθθθθϕ∂∂∂∂∂++=∂∂∂∂∂ （6.1） 令 (,,)()()()u r R r θϕθϕ=ΘΦ， 代入（6.1）得2222222111()(sin )0sin sin d dR d d d r R R r dr dr r d d r d θθθθθϕΘΦΘΦ+Φ+Θ= 以2r R ΦΘ乘上式各项得 2222111()(sin )0sin sin d dR d d d r R dr dr d d d θθθθθϕΘΦ++=ΘΦ 或2222111()(sin )sin sin d dR d d d r R dr dr d d d θθθθθϕΘΦ=--ΘΦ 上式左端只与r 有关，右端只与θ，ϕ有关，要它们相等只有当它们都是常数时才有可能。

为了以后的需要，我们把这个常数写成(1)n n +的形式（这是可以做到的，因为任何一个实数总可以写成这种形式，这里的n 可能为实数，也有可能为复数），则得21()(1)d dRr n n R dr dr=+ （6.2）22211(sin )(1)sin sin d d d n n d d d θθθθθϕΘΦ+=-+ΘΦ （6.3） 将方程（6.2）左端的导数计算出来，即有2222(1)0d R dRr r n n R dr dr+-+= 这是一个欧拉方程，它的通解为(1)12()n n R r A r A r -+=+其中12,A A 为任意常数。

勒让德多项式递推公式证明以勒让德多项式是数学中一类重要的特殊函数，其递推公式是证明其性质的关键。

本文将通过介绍以勒让德多项式的定义、性质和递推公式的证明，来解释这一标题。

以勒让德多项式是数学中的一类正交多项式，它们是解决物理和工程问题中的常微分方程的重要工具。

以勒让德多项式的定义如下：$$P_n(x) = \frac{1}{2^n n!} \frac{d^n}{dx^n} \left[(x^2 - 1)^n\right]$$其中，$n$为非负整数，$P_n(x)$表示以勒让德多项式的第$n$阶，$x$为自变量。

以勒让德多项式具有一系列重要的性质，如正交性、归一性等，这些性质使其在数学和物理学中得到广泛应用。

以勒让德多项式的递推公式是证明其性质的关键。

递推公式的形式如下：$$(n+1)P_{n+1}(x) = (2n+1)xP_n(x) - nP_{n-1}(x)$$下面我们来证明这个递推公式。

我们将以勒让德多项式的定义代入递推公式中，得到：$$(n+1)\left(\frac{1}{2^{n+1} (n+1)!} \frac{d^{n+1}}{dx^{n+1}} \left[(x^2 - 1)^{n+1}\right]\right) = (2n+1)x\left(\frac{1}{2^n n!} \frac{d^n}{dx^n} \left[(x^2 - 1)^n\right]\right) - n\left(\frac{1}{2^{n-1} (n-1)!} \frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right]\right) $$化简上式，可以得到：$$\frac{1}{2^{n+1} (n+1)!} \frac{d^{n+1}}{dx^{n+1}} \left[(x^2 - 1)^{n+1}\right] = \frac{2n+1}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right]$$我们将上式中的$n+1$分布到第一项中，并利用导数的链式法则进行化简，得到：$$\frac{1}{2^{n+1} (n+1)!} \frac{d}{dx}\left[(2n+1)x(x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right] $$再次化简上式，得到：$$\frac{1}{2^{n+1} (n+1)!} (2n+1)\left[x\frac{d}{dx}\left[(x^2-1)^n\right] + (x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right] $$继续化简上式，可以得到：$$\frac{1}{2^{n+1} (n+1)!} (2n+1)\left[x\frac{d}{dx}\left[(x^2-1)^n\right] + (x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right]$$再次化简上式，得到：$$\frac{1}{2^{n+1} (n+1)!} (2n+1)\left[x\frac{d}{dx}\left[(x^2-1)^n\right] + (x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right] $$继续化简上式，可以得到：$$\frac{1}{2^{n+1} (n+1)!} (2n+1)\left[x\frac{d}{dx}\left[(x^2-1)^n\right] + (x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right] $$再次化简上式，得到：$$\frac{1}{2^{n+1} (n+1)!} (2n+1)\left[x\frac{d}{dx}\left[(x^2-1)^n\right] + (x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right] $$通过以上推导，我们证明了以勒让德多项式的递推公式。

由达朗贝尔判别法可知，当n 0不为整数时，这两个级数的收敛半径为1,在（）式和（）式中，a°与a i可以任意取值，它们起着任意常数的作用，显然，在区间（—1，1 ）内yi和y都是方程（）的解，所以（）是（）的通解。

上面（）和（）幕级数当|x| 1时级数收敛，此外级数是发散的。

并且，我们发现，当n取非负整数时，y1和y2中有一个便退化为n次多项式，它就是方程（）在闭区间［-1,1］上的有界解。

此时，适当的选定这个多项式的最高次幕系数an，所得的多项式称为n阶勒让德多项式或第一类勒让德函数，记作P n X，下面我们来推导勒让德多项式R X的表达式。

①当n为正偶数时%退化为n次多项式。

为求得巳X的表达式，在％中我们通过a n来表示其它各项的系数。

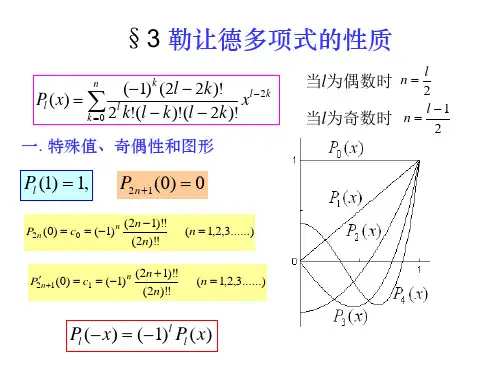
为此，将系数递推关系式改写成下列形式：(k 2)(k 1) 一a k O k 2(k n)(k n 1) 2()在（）式中取k n 2，得：n(n 1) aa n 2an2(2 n 1) n()勒让德（legendre）多项式及其性质一. 勒让德多项式勒让德多项式是由勒让德方程的通解推导出来的，所以我们首先引入勒让德方程，以及勒让德方程的幕级数解，勒让德方程的表达式如下：Q II I （1 x2）y 2xy它的幕级数解如下：y y i y2其中：2ky i a2k Xk 02k 1y2 a2k 1X ak 0n(na o[1(n1)y 02!吨X33!其中n为非负实数（）()n(n 2)(n 1)(n 3)X4]4! （）(n 1)(1 3)(n 2)(n 4)X5✓v5!]()2n 2m !an 2m1m2n m!(n m)!(n 2m)!(m 0,1,(\!7nXI2rnn- 2n/1%\IJn/(. rrX.n 2mx()般地，我们有我们将这些系数带入（）中，并把此时的 y 记作R （x ），可得:这就是当n 为正偶数时勒让德多项式 ②当n 为正奇数时丫2退化为n 次多项式，我们把丫2记作R （x ），同理可得:n 1了、2,八m(2n 2m)!p n (x)( 1) m02n m!(n m)!(n 2m)! 把（）和（）写成统一的形式，得习惯上取an 为 a n(2n)2n ( n!)2()于是有: an 2n(n 1)2n(2n 1)(2n 2)! 2(2 n1)2n n(n 1)!n(n 1)(n 2!)(2n 2)! 2)!2n(n 1)!(n()在（）式中取k n4，并利用a n 2之值得:(2n 4)!a n(n 2)(n 3)a 4(2 n 3) n 22(n 2)(n 3)| 4(2n 3) I 1)(2n 2)!2n (n 1)!(n 2)!(1)2Y(2!)(n 2)!(n 4)!()由上述讨论可知，当n 为非负整数时，力和y 2中有一个是n 阶勒让德多项式，而另一个是无穷 级数，记作Q n (x)，称为第二类勒让德函数，此时方程()通解为：y Cf n (x) C 2Q n (X )()特别当n 0,1,2,3,4,5时，由()和()式得：1 2P o (x) 1 P(x) xP 2(x) 2(3X 1) 1311 5 3F 3(x)(5x 3x)P 4(x) -(35x 4 30x 2 3)F 5(x)(63x 70x 15x) 288它们的图形如下:P n (X)m 0m —(2n 2m )!—Xn 2m2n m!(n m)!(n 2m)!()其中[2]表示 2的整数部分-05c勒让德多项式的性质首先介绍一下勒让德多项式的母函数: 试将函数(x,z)(1 2xz z2) 2() 展开成z的幂级数(x,z)nA n Zn 0()可以证明(x, z)级数展开式中z n的系数恰好是勒让德多项式, 最终得到(x,z)(1 2xz Z2) 12Fn(x)z nn 0()因此称(x, z)为勒让德多项式的母函数。