参数敏感性分析与试验方案优化_图文(精)
- 格式:doc
- 大小:279.00 KB
- 文档页数:6
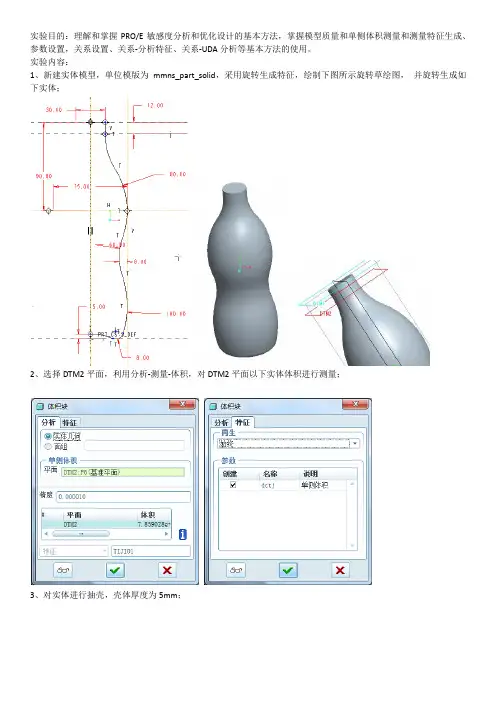
实验目的:理解和掌握PRO/E敏感度分析和优化设计的基本方法,掌握模型质量和单侧体积测量和测量特征生成、参数设置,关系设置、关系-分析特征、关系-UDA分析等基本方法的使用。
实验内容:1、新建实体模型,单位模版为mmns_part_solid,采用旋转生成特征,绘制下图所示旋转草绘图,并旋转生成如下实体;2、选择DTM2平面,利用分析-测量-体积,对DTM2平面以下实体体积进行测量;3、对实体进行抽壳,壳体厚度为5mm;4、测量DTM2平面以下在抽壳以后的体积,方法同3,请自行定义测量特征的特征名;5、利用分析工具,利用分析-关系:计算两次测量的体积差:6、进行敏感度分析,估计体积为:500000mm3的时候直径75的值;7、利用菜单-优化/可行性,执行可行性分析重构模型使得其容积为500000mm3;8、将容器内表面通过:复制-粘贴,编辑-填充,编辑-合并,拉伸切除原有实体、实体化,构造内部容积实体;9、构建草汇中心线:10、在草汇中心线上构建域点,并生成单侧测量体积特征;11、生成由“域点、草汇中心线、单侧测量体积特征”构建的组特征;12、新建UDA分析特征,分析对象为上述组特征,注意要生成图形对象;13、利用扫描混合命令构建如图扫描特征,特征变量为容积的体积:sd6=evalgraph("VOL_H",trajpar)/1000014、草汇刻度并,阵列:草汇设置扫描:sd6=evalgraph("VOL_H",trajpar)/10000阵列:if(floor(sd3/10)==sd3/10)sd5=10elseif(floor(sd3/5)==sd3/5)sd5=7.5elsesd5=5endifendif实验报告要求:1、按照学校教务提供的课程实验格式编写实验报告;2、完成实验报告,报告中包括个人对绘制方法和建模过程的理解。
3、鼓励有创新的建模设计方法;软件版本:Creo.Elements.Pro.5.0.M110.Win32.简体中文。




流体动力学模型的参数优化与敏感性分析方法引言流体动力学模型是研究和预测流体行为的有效工具。
然而,模型的准确性和可靠性取决于参数的选择。
为了优化模型并评估参数对模型输出的影响,研究者们开发了各种参数优化和敏感性分析方法。
本文将介绍流体动力学模型的常见参数优化和敏感性分析方法,并讨论它们的优缺点及应用领域。
参数优化方法1. 遗传算法(Genetic Algorithm)遗传算法是一种模拟生物进化过程的优化算法。
它通过选择、交叉和变异操作来生成新的参数组合,并根据适应度函数评估它们的优劣。
适应度函数通常是模型输出与实测数据之间的均方根误差或相关系数。
遗传算法可以帮助研究者在搜索参数空间时快速找到最优解。
2. 粒子群优化算法(Particle Swarm Optimization)粒子群优化算法是另一种基于群体智能的优化算法。
它模拟了鸟群或鱼群中个体之间的协作和信息传递。
算法中的每个粒子代表一个参数组合,并根据其自身的历史最优解和群体的最优解进行更新。
粒子群优化算法具有全局搜索能力和快速收敛性。
3. 贝叶斯优化算法(Bayesian Optimization)贝叶斯优化算法是一种基于贝叶斯统计的优化算法。
它利用模型输出与实测数据之间的先验知识来指导参数搜索过程。
算法通过更新参数的后验分布来逐步收敛到最优解。
贝叶斯优化算法适用于对高代价函数进行优化的问题,并能够在少量样本点的情况下取得较好的效果。
敏感性分析方法1. 全局敏感性分析(Global Sensitivity Analysis)全局敏感性分析通过评估模型输出与各参数之间的敏感性来确定参数对模型输出的影响程度。
常见的全局敏感性分析方法包括Sobol指数、Morris元分析方法和FAST(Fourier Amplitude Sensitivity Test)等。
全局敏感性分析可以帮助研究者识别对模型输出影响最大的参数,并优先进行优化。
2. 局部敏感性分析(Local Sensitivity Analysis)局部敏感性分析旨在评估模型在参数变化时的灵敏程度。




摩尔库伦本构模型参数敏感性分析及修正吴强1吴章利2(1.中国水电顾问集团贵阳勘测设计研究院贵州贵阳550081;2.贵州省煤田地质局地质勘察研究院贵州贵阳550081)摘要以锦屏二级电站引水隧洞为例,建立1号引水隧洞FALC3D模型,在其他参数不变的条件下,单独增大(减小)内聚力C或内摩擦角φ20%,然后模拟计算拱顶位移,对比位移大小分析得出参数C和φ对于隧道稳定性计算的敏感性。
计算结果表明,在水的作用下,对于围岩稳定性,φ的作用比C要强。
以此为依托,结合室内试验,针对锦屏二级电站引水隧洞高地应力、高外水压力条件下,提出修正的FALC3D摩尔库伦强度判别模型:τ≤0.67C+tg0.938φ。
关键字FLAC3D;摩尔库伦;敏感性;本构方程中图分类号:TV554文献标识码:A1前言选取1号引水洞(SK8+150+SK8+250)增减c或φ值20%,得到五组模拟参数组作为模拟分析对象,洞室直径为11.8m,模型合,两种对比方案,具体参见表2。
运用五组数值模拟方法中的有限差分法应用比x、z方向均取60m,大于5倍洞径,满足圆形洞参数组合分别进行模拟计算,跟踪分析在较广,比较突出的拉格朗日有限差分软件室一般模拟计算范围,y方向取洞线长100m,不同c和φ值条件下拱顶位移同其参数就是FLAC3D,操作简单,应用广泛,可以在选择通用有限元程序ANSYS建立三维模变化的规律。
隧道、滑坡、基坑等许多工程中运用,特别型,通过ANSYS到FLAC3D的转换程序,将2.2方案一模拟分析适合岩土工程。
FLAC3D有十种基本的本构建好的模型导出为FLAC通用的模型,转换在方案一参数条件下,单独变化C值模型,对于隧道围岩稳定性的研究主要运后的网格基本为四面体单元,整个模型由20%,变化后模拟计算得到的结果见图1。
用的模型就是摩尔库伦模型,14250个单元和15367个节点组成。
对拱顶顶点进行位移跟踪,可以得到在其运用FLAC3D对隧洞进行模拟,在不同对于模型的边界条件,为了达到既符他参数不变的条件下:C值不变时(C=1.的工程地质条件下,参数选取至关重要,针合实际情况,又避免边界发生破坏的目的,0MPa、ф=30°)拱顶位移为2.18cm;单独对锦屏二级电站引水隧洞高地应力和高外模型前后左右边界(x方向)采取水平约束,减小C值20%时拱顶的位移为2.23cm;增水压力的工程地质条件下,需要考虑岩体上下重力方向(z方向)上底面不约束,下底大C值20%时拱顶位移为2.09cm。


作物学报 ACTA AGRONOMICA SINICA 2024, 50(2): 464 477 / ISSN 0496-3490; CN 11-1809/S; CODEN TSHPA9 E-mail:***************本研究由国家自然科学基金项目(32160416), 甘肃省教育厅产业支撑计划项目(2021CYZC-15, 2022CYZC-41)和甘肃省优秀研究生“创新之星”项目(2022CXZXS-026)资助。
This study was supported by the National Natural Science Foundation of China (32160416), the Industrial Support Program of Gansu Provin-cial Education Department (2021CyzC-15, 2022CYZC-41), and the “Innovation Star” Project of Gansu Province Outstanding Postgraduate Students (2022CXZXS-026).*通信作者(Corresponding author): 聂志刚,E-mail:**************.cn第一作者联系方式:E-mail:*****************Received (收稿日期): 2023-03-12; Accepted (接受日期): 2023-09-13; Published online (网络出版日期): 2023-10-11. URL: https:///urlid/11.1809.S.20231010.1346.002This is an open access article under the CC BY-NC-ND license (/licenses/by-nc-nd/4.0/).DOI: 10.3724/SP.J.1006.2024.31018温度升高下APSIM 模型春小麦籽粒生长参数敏感性分析及优化张 康1 聂志刚1,* 王 钧1 李 广21甘肃农业大学信息科学技术学院, 甘肃兰州 730070; 2 甘肃农业大学林学院, 甘肃兰州 730070摘 要: 为有效识别基于APSIM 模型籽粒生长参数中春小麦产量敏感性参数, 快速并准确的估算当地模型参数。
流溪河模型云计算与服务平台中山大学水灾害管理与水利信息化实验室∙首页∙理论方法o理论方法o建模数据o参数敏感性o参数优选o单元分类o断面估算o参数分类∙应用案例o新安江水库o乐昌峡水库o长湖水库o流溪河流域∙论文论著∙科技团队∙大记事∙软件系统∙新手上路∙我的模型∙联系我们∙理论方法∙建模数据∙参数敏感性∙参数优选∙单元分类∙断面尺寸估算∙参数分类1、参数敏感性分析方法流溪河模型将参数分成高度敏感参数、敏感参数和不敏感参数。
由于流溪河模型的参数较多,那些参数是高度敏感参数,那些参数是敏感参数,那些参数是不敏感参数,就需要通过敏感性分析确定。
参数敏感性分析分参数逐个进行,一次仅进行一个参数的敏感性分析。
将当前进行敏感性分析的参数称为分析参数,其它参数称为非分析参数。
敏感性分析的具体方法是,固定所有非分析参数的值不变,对分析参数,以其现值为中心,上、下各取若干个值分别进行洪水模拟计算,求出洪水模拟结果的变化随参数值变化的规律,以此判断参数是否敏感,原则上,当参数的值变化时,模拟的洪水过程有剧烈变化或较大变化时,该参数为高度敏感参数;当参数的值变化时,模拟的洪水过程有明显变化时,该参数为敏感参数;当参数的值变化时,模拟的洪水过程有一定变化,但不明显时,该参数为不敏感参数。
对流溪河模型各可调参数,逐个进行敏感性分析,包括河道单元糙率、边坡单元糙率、土壤饱和含水率、田间持水率、凋萎含水率、饱和水力传导率、土壤层厚度、土壤特性参数b、蒸发系数、潜在蒸发率和地下径流消退系数共11个参数。
在进行模型可调参数的敏感性分析时,为了全面、深入的进行分析,得到较为合理的结论,一般要选择1-3场洪水进行敏感性分析。
如何对参数的敏感性进行评判,一般通过分析由于参数变化引起的模型模拟结果变化的程度来判别。
如当参数发生一定比例的变化时,引起的模型模拟计算结果的变化幅度较大,并且其变化幅度大于参数的变化幅度时,可认为该参数是敏感的,如引起的模型模拟计算结果的变化幅度特别大,则可认为该参数是高度敏感的。
机械设计中的参数优化与敏感性分析概述:机械设计中的参数优化与敏感性分析是一种重要的工程方法,通过对设计参数的优化和敏感性分析,可以提高机械系统的性能和可靠性。
本文将介绍参数优化和敏感性分析的概念和方法,并探讨其在机械设计中的应用。
一、参数优化的概念和方法参数优化是指在给定设计目标和约束条件的情况下,通过调整设计参数来寻求最佳设计方案的过程。
在机械设计中,参数优化可以应用于各个层面,包括零件设计、装配设计和系统设计等。
参数优化的方法包括传统方法和现代方法,传统方法主要通过经验和试错来确定设计参数的最佳取值,现代方法则基于数值仿真和优化算法,能够在更大的设计空间中搜索最佳解。
二、敏感性分析的概念和方法敏感性分析是指通过对设计参数进行变化和分析,评估设计参数对设计目标的影响程度的过程。
敏感性分析可以帮助设计人员了解不同设计参数的重要性,从而指导参数优化的过程。
敏感性分析的方法有多种,常见的方法包括局部敏感性分析和全局敏感性分析。
局部敏感性分析通过计算参数的一阶和二阶导数来评估参数的敏感性,全局敏感性分析则通过采样和统计分析的方法来评估参数的重要性。
三、参数优化与敏感性分析的应用参数优化和敏感性分析在机械设计中有广泛的应用。
以某机械装配设计为例,通过参数优化,可以调整零件尺寸、连接方式和材料等设计参数,以提高装配的精度和可靠性。
同时,通过敏感性分析,可以评估不同参数对装配性能的影响,从而确定对装配质量最为关键的设计参数。
参数优化和敏感性分析还可以应用于机械系统设计中,例如在发动机设计中,可以通过参数优化来提高燃油效率和排放性能,通过敏感性分析来评估不同参数对发动机性能的影响。
四、参数优化与敏感性分析的挑战和发展方向参数优化和敏感性分析在机械设计中面临一些挑战,例如设计空间的高维度和非线性、多模态性和优化过程的计算成本等。
为了应对这些挑战,需要发展更为高效和精确的优化算法和敏感性分析方法。
同时,还需要开展参数优化和敏感性分析的多学科集成研究,将机械设计与其他学科(如材料科学、流体力学和动力学等)相结合,以实现更为综合和优化的设计。
岩土力学 ! 年态时著法。
, Υ 、甲、值的变化将影响结构的变形特性并随塑性区的增大而对结构变形的影响愈加显的敏感度不仅与其本身的基准值有关 , 一即Γ , , 还与 & 二、叮, 的取值有关 , , 。
如欲进一步考虑这种参数间的相关影响’! 〔应对所讨论的问题具备一定的专业知识。
也可以应用正交试验对与其它参数相。
或灰色系统理论“’ 等 , 对参数间的相关作用进行预分析 , 经过预分析关性显著的参数进行敏感性分析时应同时令其相关参数在可能的范围内变化试验方案优化对地下工程进行稳定性分析因 , , 需要了解场地各种有关的岩体力学参数。
精确的岩体力学、参数只有通过大型原位试验才能得到又不可能大量进行因此 , 。
而大型原位试验由于费用高 , 、强度大时间长等原另一方面 , , 并不是每种岩体力学参数都必须通过大型原位试验获进行试验方案优化 , 是一个非常值得我们研得。
如何根据实际问题合理安排试验究的课题试验方案优化的含义是 , 以最小的大型原位试验工作量 , 获得足以满足工程所需精度要求的各种岩体力学参数。
参数敏感性分祈为试验方案优化提供了基础 , = 0 > 根据参数敏感度因子排
序。
可将岩体力学参数区分为主要参数和次要参数 , , 从而抓住主要矛盾。
例如 , 对于高边墙的水平变形而言。
水平向地应力 & , 和岩体弹性模量 6 就 , 是主要参数 , 而其它参数是次要参数 , 主要参数必须通过大型原位试验获得 , 。
而次要参数则。
只需通过室内试验获得 , 甚至不通过试验。
而通过以往试验结果类比或凭经验获得前面我们已阐述 , , =
7 > 参数敏感性分析可以避免主观错误判断对于不同的基准参数 , 集
参数敏感度排序是不同的 , 因此 , 应针对具体工程问题。
进行参数敏感性分析来区分主要参数和次要参数 = ! > 而不应单凭经验行事 , 根据各主要岩体力学参数的敏感度因子的对比原则上讲 , 合理安排这些参数原位试验的相。
应试验量 = 。
, 敏感度越高的参数 0 , 应安排的试验
量越多 , > 根据敏感度因子和工程要求精度选择合适的试验方法 , 比方说7 , 测量“ ‘, 。
的方二法有两种选择∗Ζ , 方法。
的相对误差 ( , 。
二, ≅二Ζ ≅ 1 费用比较便宜 , , 方法“ 的相对误差 ( , 5 ≅费用较贵。
、二由敏感度分析知 1 . 。
∗Ρ Ρ 故两种方法的测量误差引起“ 的相对误差分别为( Ξ , 7 Ζ和 ! 。
Π “5 二∗7 Ρ Ζ 。
若要求的相对误差Π [ Ζ “ , 则方法 , 尽管费而不
必一 , 用低也不应采用而应采用方法。
尚若工程要求 ( [ 7 ∗ Ζ 。
则应采用方法味追求精度去采用方法 7 敏感性分析从工程精度角度为试验方案优化提供了依据合试验费用、进行试验方案优化时还应结设备条
件等因素 , 统筹考虑。
结束语。
敏感性分析是系统分析中评价系统抗干扰能力的一种有效方法析的基础上 , 本文在单因素敏感性分。
定义了无量纲敏感度函数和敏感度因子 , 使得多因素的敏感性具有可比
性
第期章光等 5 参数敏感性分析与试验方案优化 , 作为算例评价指标次为 5 , 本文对拉西瓦地下工程的稳定性进行了敏感性分析 , 。
应用本课题组编制的二、维非线性有限元程序建立了计算模型以地下主厂
房高边墙的最大水平向变形作为稳定性的娜、考察了岩体弹性模量『, 1 6 、泊松比。
内聚力 , , Υ 、内摩擦甲 1 水平向地应力 , 叮二 , 和铅垂向地面力等参数的扰动影响 , , 经过分析刀5 、得到了各参数敏感度值 4 按大
小排序。
4 依 , , 傲Ω 」, 水平向地应力指出, Ω 一Δ 5 ,, 二≅∗Ρ , 4 Η1 一一 4 『, 4 一4 二 , 和弹模 6 是影响高边墙水平向变形的敏感参数二习共≅。
1 ∗, , Δ 。
, 5 ≅ 4 ≅ , 4 ∗ 1 ∗ςς , 4一一Ω Δ 5 , ≅∗∗! Ω , 。
Δ , 。
Ω 一 4 其余为不敏感参数 4 人、 ? ≅∗ , 1 ∗7 ∗ ‘, 一结果表明。
、。
4 。
但应基准Ω 上
述结论是在参照拉西瓦工程的实际条件而给出的基准参数集的基础上得到的 , 。
参数集不同结论将有差异 , 。
本文提出了试验方案优化
的概念。
参数敏感性分析是试验方案优化的基础 , 。
通过参数敏。
感性分析和敏感度因子排序要参数 , 可以针对各种不同的具体情况 , 确
定符合实际的主要参数和次结合实际工程所要求的精度 , 做到最合理地安排试验量和选择合适的试验方法、在本文进行的有限元计算过程中在此表示衷心感谢。
得到了潘榕明先生王平先生和王可钧先生等同事的热情帮助 , 参于学馥等李世辉曾秋成 1 1 1 考 5 文献 , 地下工程围岩稳定分析 1 1 北京 5 煤炭出版社Ρ! , 隧道围岩稳定系统分析技术数理统计
方法 1 1 北京 5 中国铁道出版社 1 合肥安徽科学技术出版社系统工程, Ρ ∗ 1 李健萍等影响石膏强度因素的灰色关联分析 , 磅
Ρ 岩土力学 ! 年8& 3 & Τ ∃ Η ∃ 3 Δ ∃∋ . −Η −ϑ−ΗΚ Φ∋ & 0 Κ . −. & ∋( # ; Η−Τ −∴ −∋ Λ < # 3 ] ∃ . Η 83 # Λ 3 & Τ Χ ,& 忍 . ⊥ Ι & 忆夕Χ ,“ Γ _ Η ∃泞,∃
艺” Φ ⎯. Η 3& Μ∋ Η 、 < 1 ; & ;∃ # ∋ 3 , ⎯1 & ∋ .∃ 1 ( # ∋ .∃∋ , Η ,∃ϑ也∃ −Η Κ Η ,# ( < & Γ # < , −∋ Λ 0 ∃一; Ψ −Η & 3 & Τ ∃ Η ∃ 3 .∃∋ . − Η −ϑ−Η Κ & 3 ∃& ∋ & 0 Κ, ∋∃ , & # .∃∋ Θ −Η − ϑ−Η Κ 3 ∃ .Ι Ι ∋ Γ Η − ( −Η − & Η# 3 Ι , ( −Τ
8&3 & ∃∋ . − # ∋ 0 ∃ . . ∋∃ .. ( 1 ∃ <− ( Η Τ & %∃ , Η 五∃ ,∃ − ∋ 0Η . # < . ∃∋ . −Η − ϑ−Η Κ & ∋ 0Κ . − , −∃ ( # ∋ Τ Η # ∋ 0 Η −8 0 ∃ Η Τ ∃ Η∃ # 3 . Γ # Τ 8& 3 −Ψ & & ⎯ 0∃ ( ∃∃ Φ. 3 & ∋∃ Α & Τ 80 ∃ Η 3 . ∃∋ . −Η − ϑ−Η Κ ∃ 3 ∃ . Ι & ∋ & 0 Κ. − , Γ & 3 3 # Ι # ∋ ,∃ . Η& Η & ⎯ −0 −Η Κ < α 『1 & Α 胜∋ Λ 3 # Ι ∋ ( # ∃∋ Λ
−∋ 0 # ∃∃Θ Λ 1 ] , 0 Η. . , # Ψ Η Η, & Η Η , ∃ , ∃ # 3 − , Η & 0 Η Γ 3 Ι . 0 . Η 3 ∃ .. & ∋ ( Η # ∋ , ∃ 0 & . Η − Γ Τ &Η ( ∋ Ι Ι . # < Η ,# 3 # ∃ % ∃ Τ & 吕! 6 & 3 ∃ ,∃ 1 ∃∋ . −Η − , 8 ( ∃ & 3 & Τ ∃∃ 3 . & << 扭Γ Η −∋ 1 Λ Η ,∃∃ ,# & ∋ & 3 −∴ Η∋ & 0 ( ∃ <# Τ −# Η < Η,∃ ‘−Λ , Η −ϑ∃ . −( Ψ & 00. 3 . # < Η ,∃ 3 ∃ Ι ∋ ( ∃∃ 3 Λ Η 3 # Ι
∋ <& − 3 Γ Η # 3 & . ∃ Κ ⎯Ι − 0 ( −∋ Λ ], . ∃ 0 Κ . −. 0. # 8 Η −# . ∋ , # Ψ . # ,&Η # ∃∋ . ∴ 0 −Θ 8 Η∃ & 3 & Τ ∃ Η∃ & 3 ∃ 0 Η & Η ( 3 # Η , ⎯ 8 & 3 & ∋ Κ ∃Η# 3 Η 1 ] , ∃ Γ # ∋ Γ ∃ < Η # 8Η −Τ − − Λ < < # # 3 “Η ;3 # Λ 3 & Τ Η ∃ , ; Ι <# 3 & Ψ . 1 & 3 ( −∋ Η, ∃ 8 & 8∃ 3 & ∋ ( .∃∋ β − Η −ϑ−Η Κ & ∋ & 0 Κ . −1 , # ⎯&.∃ # 8 Η − Τ −∴−∋ Λ <# 3 Η 83 # Λ Τ 之 . ∃∋ . Β∃ Κ _ # 3( , ? ; & 3 & Τ ∃ Η ∃ 3 , − Η −ϑ−Η Κ &∋ & 0Κ . −. , # 8 Η − Τ −5 − ∋ Λ 祥。