实验优化设计第4章方差分析
- 格式:ppt
- 大小:463.00 KB
- 文档页数:40

方差分析的实验报告方差分析的实验报告引言:方差分析是一种常用的统计方法,用于比较两个或多个组之间的均值差异是否显著。
在本次实验中,我们将运用方差分析来研究三种不同肥料对植物生长的影响。
通过对不同处理组的生长情况进行观察和数据分析,我们旨在探究不同肥料对植物生长的影响是否存在显著差异。
实验设计与方法:本实验采用了完全随机设计,共设置了四个处理组,分别为对照组和三个不同肥料处理组。
每个处理组设置了十个重复样本。
实验的主要步骤如下:1. 准备工作:选取相同品种的植物作为实验材料,并确保它们具有相似的生长状态和健康状况。
同时,为了消除外界因素的干扰,我们将植物放置在相同的环境条件下。
2. 分组处理:将植物随机分为四组,其中一组作为对照组,不施加任何肥料,另外三组分别施加三种不同的肥料。
3. 数据收集:在实验开始后的每个固定时间点,我们测量每个植物的生长指标,如株高、叶片数、根长等,并记录下来。
这些数据将用于后续的方差分析。
数据分析与结果:在实验结束后,我们对收集到的数据进行了方差分析。
通过计算各组的平均值、方差和标准差,我们得到了以下结果:1. 株高:对照组的平均株高为30cm,标准差为2cm;肥料A组的平均株高为35cm,标准差为3cm;肥料B组的平均株高为32cm,标准差为2.5cm;肥料C组的平均株高为33cm,标准差为2.8cm。
方差分析结果显示,不同处理组之间的株高差异是显著的(F=4.56, p<0.05)。
2. 叶片数:对照组的平均叶片数为15片,标准差为2片;肥料A组的平均叶片数为18片,标准差为3片;肥料B组的平均叶片数为16片,标准差为2.5片;肥料C组的平均叶片数为17片,标准差为2.8片。
方差分析结果显示,不同处理组之间的叶片数差异是显著的(F=3.21, p<0.05)。
3. 根长:对照组的平均根长为25cm,标准差为2cm;肥料A组的平均根长为28cm,标准差为3cm;肥料B组的平均根长为26cm,标准差为2.5cm;肥料C组的平均根长为27cm,标准差为2.8cm。



实验设计及数据分析-方差分析实验设计及数据分析方差分析一、方差分析的基本原理方差分析的核心思想是将观测值的总变异分解为不同来源的变异,然后通过比较不同来源变异的大小来判断因素对观测结果的影响是否显著。
总变异可以分解为组间变异和组内变异。
组间变异反映了不同组之间的差异,组内变异则反映了组内个体之间的随机误差。
如果组间变异显著大于组内变异,就说明不同组之间的均值存在显著差异,即所研究的因素对观测结果有显著影响。
二、实验设计要点1、确定研究因素和水平首先要明确研究的因素,以及每个因素的不同水平。
例如,研究不同肥料对作物产量的影响,肥料种类就是因素,不同的肥料品牌或配方就是水平。
2、选择合适的实验对象实验对象应具有代表性和随机性,以减少偏差。
3、控制无关变量在实验过程中,要尽量控制其他可能影响结果的无关变量,以确保结果的准确性。
4、确定样本量样本量的大小会影响统计检验的效力,一般来说,样本量越大,结果越可靠,但也要考虑实际操作的可行性和成本。
5、随机分组将实验对象随机分配到不同的组中,以保证各组之间的初始条件相似。
三、方差分析的类型1、单因素方差分析只考虑一个因素对观测结果的影响。
2、双因素方差分析同时考虑两个因素对观测结果的交互作用。
3、多因素方差分析涉及两个以上因素的情况。
四、数据分析步骤1、提出假设零假设(H0):不同组之间的均值没有显著差异。
备择假设(H1):不同组之间的均值存在显著差异。
2、计算统计量根据实验数据,计算出组间平方和、组内平方和、总平方和等,进而得到 F 统计量。
3、确定显著性水平通常选择 005 或 001 作为显著性水平。
4、查找临界值根据自由度和显著性水平,在 F 分布表中查找临界值。
5、做出决策如果计算得到的 F 统计量大于临界值,拒绝零假设,认为不同组之间的均值存在显著差异;否则,接受零假设。
五、结果解读1、查看 ANOVA 表ANOVA 表中会给出各项变异的来源、自由度、平方和、均方和 F 值等信息。


▪ 习题4.1不能用正交表78(2)L ,因为会产生混杂。
需选用正交表1516(2)L 。
表头设计如下:▪ 说明:也可有其他不同的表头设计(试验方案)。
▪ 习题4.2 由于1AB C D A B A C B C f f f f f f f ⨯⨯⨯=======, 7f =总,故可选用正交表78(2)L ,且不会产生混杂。
表头设计如下:根据直观分析结果,因素的主次顺序为:AXB AXC C B BXC A D A 与B 的二元表,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,A 与C 的二元表,▪根据A与B的二元表,A1 B2的效果最好;▪根据A与C的二元表,A1 C2的效果最好;▪从直观分析结果可以得到,D1效果最好;▪故最优生产条件为:A1 B2 C2 D1▪(3)方差分析由于没有误差列,故不能对各因素进行显著性检验。
但是,我们选择离差平方和最小的因素D所在的列作为误差列,对各因素进行显著性检验,得到结果如下:因素的主次顺序与直观分析的一样,从显著性来看,只有AXB显著,其他的因素或交互作用都不显著。
▪习题4.3其中A ×B 的离差平方和349.85222.29632.148A B SS SS SS ⨯=+=+=A ×B 的自由度,,,,,,344A B f f f ⨯=+=32.14841.973 5.14024.446A B F ⨯==<故A ×B 不显著。
B ×C 的离差平方和81134.7417.6342.371B C SS SS SS ⨯=+=+=B ×C 的自由度,,,,,,8114B C f f f ⨯=+=42.3714 2.601 5.14024.446B CF ⨯==<故B ×C 不显著。
▪ 因素的主次顺序(根据极差大小或F 值大小) A D F BXC AXB B E C ▪ 最优工艺条件的确定:可以根据直观分析结果选择每个因素的最优水平,得到最优工艺条件为:,,,,,,,,,,,,,,,A1,D1,F1,E0,B0,C0,,.,,,,,,,,,,也可以计算各因素的水平效应 根据水平效应来确定,具体如下: 对于因素A ,,,,115221319ˆ9.148927927A K T a=-=-= 224251319ˆ 1.630927927A K T a =-=-=-333721319ˆ7.519927927A K T a =-=-=-故A 的第1水平的效应最大。

方差分析实验报告一、实验目的:1.学习和掌握方差分析的基本原理和方法。
2.通过实验数据的处理,在不同的水龄条件下,比较水体COD浓度之间的差异,从而分析水龄对COD浓度的影响。
二、实验原理:1.方差分析是一种用来比较不同处理组之间差异性的统计方法。
它可以将总体方差分解为由不同因素引起的组内变异和组间变异,从而确定组间差异是否显著。
2.实验中所用的单因素方差分析是一种简单的方差分析方法,用于比较各组间的均值差异。
三、实验方法:1.实验设计:选取三个不同的水龄条件(10天、20天、30天)进行实验。
2.实验过程:分别采集三个水龄条件下的水样,进行COD浓度的测定。
每组实验重复三次,共计九次测定。
四、实验数据:1.实验数据见附表一2.通过对实验数据的处理,得到各组的均值和方差。
五、数据处理:1.计算总平均数:将所有测定值相加,然后除以测定的总次数。
2.计算组间平均数:将每组测定值相加,然后除以每组测定的次数。
3.计算组内平均数:将每个水龄条件下的测定值相加,然后除以该水龄条件下的测定次数。
4.计算组间平方和和组内平方和。
5.计算组间均方和和组内均方和。
6.计算F值。
7.查找F分布表,确定显著性水平α下的F(α)值。
8.判断各组均值之间的差异是否显著。
六、结果分析:1.通过计算可得,总平均数为X,组间平均数为X1、X2、X3,组内平均数为X1、X2、X32.计算得到组间平方和为SSB,组内平方和为SSW,组间均方和为MSB,组内均方和为MSW。
3.计算得到F值为F=MSB/MSW。
4.查找F分布表,确定显著性水平α下的F(α)值。
若F>F(α),则拒绝原假设,即各组之间的均值差异显著。
5.若各组均值差异显著,则可以进一步比较各组均值之间的差异。
七、实验结论:1.经过方差分析得知,在水龄条件下,水体COD浓度之间存在显著差异。
2.进一步比较各组均值之间的差异,可以得到水龄越长,水体COD浓度越高的结论。


第4章方差分析(ANOV A)实验设计和分析Catherine Potvin4.1生态学问题弄懂生态学问题需要将各种环境因子的影响分开,生态工作者用实验来解决这个问题。
不论在野外还是在控制环境条件下,可控实验都可以让生态工作者们只变化一个因子来检验其影响。
例如,生长箱能使生物体生长在完全相同的温度而不同的光周期的条件下,或相同的光强而不同温度条件下的实验成为可能。
在控制实验中,通常最希望的情况是环境‘背景’,即所有的影响因子, 不是自由地变化,而是精确地得到控制,这样就能够保证在改变目标变量时,观测的反应不会受到其它因素的影响。
因而控制环境条件, 例如使用生长箱和温室,成为植物生态学的一个常用的方法,如同动物生态学中使用的生长柜和水族槽一样。
本章第一部分,我要讲一下作为实验生态学基本工具的方差分析(ANOV A)。
本章重点放在实验设计上。
虽然人们一般认为生长箱会提供同一环境条件,但不论在一个生长箱内还是生长箱间都存在环境异质性(Lee和Rawlings 1982;Potvin等1990a),因而能够充分处理环境异质性的实验设计将在本章中述及。
尽管我的论述主要是以生长箱实验为基础,其原理在其它类型的控制或野外环境的实验研究中同样适用(第5,15和16章)。
我还要讨论错误实验设计的代价。
本章应视为实验设计的起步点,这个起步点就是要考虑各种影响因素。
实验者通常进行的实验比这里展开的要复杂。
但是一旦懂得了基本原理,讨论各种实验设计就相对简单一些。
更详细的论述请见Cochran & Cox(1957)和Winter(1991)。
4.2 统计问题:环境变化与统计分析正如Underwood(1997)建议的一样,生态实验设计的第一步是建立一个线性模型使研究者能够将感兴趣的变量(因素)独立出来。
由于实验设计支配误差项,建立线性模型取决于所研究的因子以及具体的实验设计。
在任何一个实验开始时,最基本的是要检验空间与时间变化的格局。
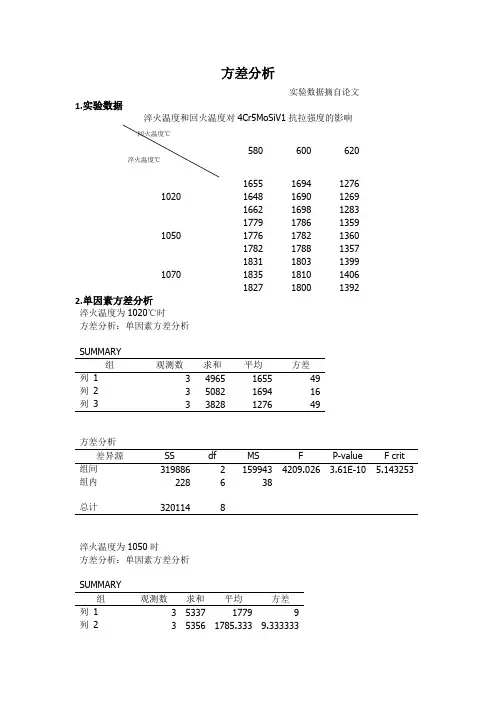
方差分析实验数据摘自论文1.实验数据淬火温度和回火温度对4Cr5MoSiV1抗拉强度的影响回火温度℃淬火温度℃580 600 6201020 1655 1694 1276 1648 1690 1269 1662 1698 12831050 1779 1786 1359 1776 1782 1360 1782 1788 13571070 1831 1803 1399 1835 1810 1406 1827 1800 13922.单因素方差分析淬火温度为1020℃时方差分析:单因素方差分析SUMMARY组观测数求和平均方差列1 3 4965 1655 49列2 3 5082 1694 16列3 3 3828 1276 49方差分析差异源SS df MS F P-value F crit 组间319886 2 159943 4209.026 3.61E-10 5.143253 组内228 6 38总计320114 8淬火温度为1050时方差分析:单因素方差分析SUMMARY组观测数求和平均方差列1 3 5337 1779 9列2 3 5356 1785.333 9.333333列3 3 4076 1358.667 2.333333方差分析差异源SS df MS F P-value F crit组间358764.7 2 179382.3 26039.37 1.53E-12 5.143253组内41.33333 6 6.888889总计358806 8淬火温度为1070摄氏度时方差分析:单因素方差分析SUMMARY组观测数求和平均方差列1 3 5493 1831 16列2 3 5413 1804.333 26.33333列3 3 4197 1399 49方差分析差异源SS df MS F P-value F crit组间351630.2 2 175815.1 5774.949 1.4E-10 5.143253组内182.6667 6 30.44444总计351812.9 82.无重复双因素分析方差分析:无重复双因素分析SUMMARY 观测数求和平均方差行1 3 4625 1541.667 53314.33行2 3 4924 1641.333 59796.33行3 3 5033 1677.667 58437.33列1 3 5265 1755 8176列2 3 5283 1761 3439列3 3 4034 1344.667 3936.333方差分析差异源SS df MS F P-value F crit 行29749.56 2 14874.78 43.97208 0.001893 6.944272 列341742.9 2 170871.4 505.1217 1.56E-05 6.944272误差1353.111 4 338.2778总计372845.6 83.有重复双因素分析方差分析:可重复双因素分析SUMMARY580600620总计1020观测数 3 3 3 9求和4965 5082 3828 13875平均1655 1694 1276 1541.667方差49 16 49 40014.251050观测数 3 3 3 9求和5337 5356 4076 14769平均1779 1785.333 1358.667 1641方差9 9.333333 2.333333 44850.751070观测数 3 3 3 9求和5493 5413 4197 15103平均1831 1804.333 1399 1678.111方差16 26.33333 49 43976.61总计观测数9 9 9求和15795 15851 12101平均1755 1761.222 1344.556方差6150.5 2622.444 2973.778方差分析差异源SS df MS F样本89584.3 2 44792.15 1783.758 P-value F crit 列1026343 2 513171.7 20436.04 2.03E-21 3.554557 交互3937.481 4 984.3704 39.20059 6.21E-31 3.554557 内部452 18 25.11111 1.18E-08 2.927744总计112031726。