假设检验案例集
- 格式:doc
- 大小:27.00 KB
- 文档页数:6
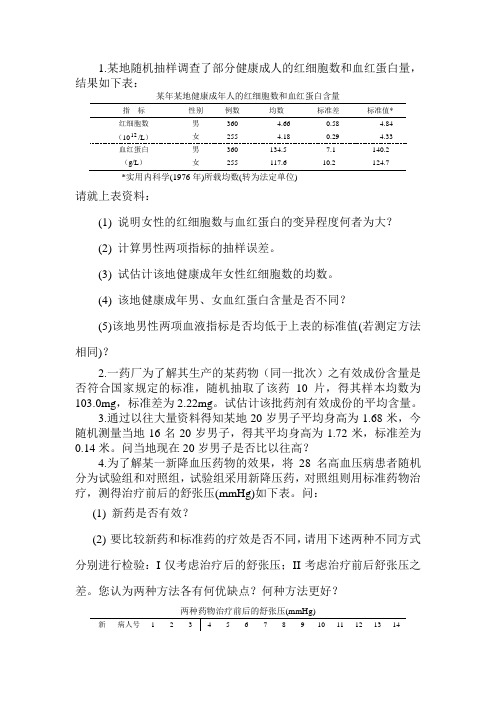
1.某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量,结果如下表:某年某地健康成年人的红细胞数和血红蛋白含量指标性别例数均数标准差标准值*红细胞数男360 4.66 0.58 4.84(1012/L)女255 4.18 0.29 4.33血红蛋白男360 134.5 7.1 140.2(g/L)女255 117.6 10.2 124.7*实用内科学(1976年)所载均数(转为法定单位)请就上表资料:(1)说明女性的红细胞数与血红蛋白的变异程度何者为大?(2)计算男性两项指标的抽样误差。
(3)试估计该地健康成年女性红细胞数的均数。
(4)该地健康成年男、女血红蛋白含量是否不同?(5)该地男性两项血液指标是否均低于上表的标准值(若测定方法相同)?2.一药厂为了解其生产的某药物(同一批次)之有效成份含量是否符合国家规定的标准,随机抽取了该药10片,得其样本均数为103.0mg,标准差为2.22mg。
试估计该批药剂有效成份的平均含量。
3.通过以往大量资料得知某地20岁男子平均身高为1.68米,今随机测量当地16名20岁男子,得其平均身高为1.72米,标准差为0.14米。
问当地现在20岁男子是否比以往高?4.为了解某一新降血压药物的效果,将28名高血压病患者随机分为试验组和对照组,试验组采用新降压药,对照组则用标准药物治疗,测得治疗前后的舒张压(mmHg)如下表。
问:(1)新药是否有效?(2)要比较新药和标准药的疗效是否不同,请用下述两种不同方式分别进行检验:I仅考虑治疗后的舒张压;II考虑治疗前后舒张压之差。
您认为两种方法各有何优缺点?何种方法更好?两种药物治疗前后的舒张压(mmHg)药治疗前102 100 92 98 118 100 102 116 109 116 92 108 102 100 治疗后90 90 85 90 114 95 86 84 98 103 88 100 88 86标准药病人号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 治疗前98 103 110 110 110 94 104 92 108 110 112 92 104 90 治疗后100 94 100 105 110 96 94 100 104 109 100 95 100 855.某医师观察某新药治疗肺炎的疗效,将肺炎病人随机分为新药组和旧药组,得两组的退热天数如下表。


假设检验在质量管理中的应用摘要:随着市场的不断完善,假设检验理论在质量管理中的重要性与日俱增,作为一种由样本信息推断总体特征的数理统计方法,在生产的各个方面都得到了广泛的应用。
本文从实际出发,对国内外研究现状进行了简要的综述,阐述了假设检验理论的基本原理,具体的实施步骤,以及在应用中需要注意的问题,同时将假设检验应用到实际的产品质量控制当中,对相关产品的质量做出合理的结论,为管理者进行改进产品质量的决策提供一定的依据。
关键词:假设检验应用质量管理Hypothesis Testing in the Application ofQuality ManagementAbstract: With the developing of the market,hypothesis testing plays an more important role in quality management.As a mathematical statistical method to make statistical inference in total population from the sample information,it is widely used in many aspects of product.This article summarizes the status of the foreign and domestic explorations.It also introduces the hypothesis testing theory,its steps ,the problems that we should pay attention to and apply it into real product quality control.It can make some conclusion of correlative product.It also can provide basis for the manager to make decision on improving product quality.Key Words: hypothesis testing application quality management在现实的生产生活中,为了取得更好的经济和社会效益,企业单位会在产品生产的各个阶段进行控制,以便达到生产预期效果,达到计划目标。

【关键字】解决案例名:对饮酒对工作能力是否有显著的影响的假设检验分析姓名:范晓维班级:人力031学号:07提交时间:用假设检验方法解决实际问题一:假设检验实际案例:任选19个工人分成两组,让他们每人做一件同样的工作,测得他们的完工时间(单位:分钟)如下:饮酒者 30 46 51 34 48 45 39 61 58 67 未饮酒者 28 22 55 45 39 35 42 38 20 问:饮酒对工作能力是否有显著的影响?(显著水平α=0.05)二:就案例中所面临的问题进行分析随是社会科学的快速发展,各种设施越发齐全,饮酒给大家带来快乐的同时也经常给大家带来不少的困扰和麻烦,甚至危急生命!本案例就饮酒是否对工作能力有影响做了一个假设检验的案例。
这个案例的特点是先提出了一个假设,然后要求从样本出发检验它是否成立,这就是假设检验问题。
假设检验的基本步骤:1:根据问题的性质和要求,提出零假设H0和备择假设H12:构造一个合适的统计量Q,它必须与假设有关,并且在H0成立的情况下,统计量Q的分布是已知的3:给定显著性水平α,确定H0的拒绝域W4:由样本观测值计算出统计量Q的值Q05:对假设H0做出判断:若统计量的值Q0落如拒绝域W内,则拒绝H0,否则接受H0对上题求解:解设两组工人的完工时间分别为总体ε~N(μ1,σ12)和η~N (μ2 ,σ22),其中σ1,σ2 未知,但假设以知有σ1=σ2,问题相当于要检验H0: μ1 = μ2是否成立。
m=10, =47.9,Sx2=125.29,n=9, =36.0, Sy2=112.00,Sω===11.5323T=(- )=2.2458对α=0.05,m+n-2=17,查t分布表,可得由于=2.2458>2.1098,因此拒绝H0: μ1 = μ2,从检验得出的结论是:饮酒对工作能力有显著的影响。
用SPSS的方法:Independent-Samples T Test 过程Analyze-Compare means-Indepant Samples T test附页:数理统计学及其应用领域数理统计学是“数学的一个分支学科。

假设检验的案例与应用摘要假设检验又称显著性检验,是统计推断的重要组成部分,其目的是在一定假设的基础上,用样本推断总体,检验实验组与对照组之间是否存在差异,差异是否显著。
在工程实践中,为了保证系统和部件的可靠性,需要建立相应的数学模型,采用概率分布和假设检验的方法进行必要的计算。
本文总结了假设检验处理检验数据的过程,并举例说明了该过程的应用。
本文首先分析了假设检验的基本思想、步骤、检验原理以及假设检验的方法等,重点讨论了假设检验在生产实践中的使用状况,丰富了假设检验在生活中的应用方面的结果。
关键词:假设检验;参数分析;实例验证1引言目前,在日常生活中,假设检验对生活和工作有着至关重要的作用,人们面对问题经常会使用假设检验进行思考,这样就可以降低人们自身因素带来的偏差,从而最大程度避免结果的不确定性给人们生活带来的影响。
通过实例的调查,可以进而拓展对假设检验的理论研究。
在现实生活中,建立的模型和解法被讨论,模型被完全讨论。
这些原则为将来假设检验在多个行业的应用提供了思路。
通常假设检验多是用在有针对性的解决问题,对问题进入深入的探讨,方案的制定等等方面。
所以,科学技术的发展,以及当前社会生活的进步都离不开假设检验。
从当前学术界关于假设检验的相关研究来看,研究成果十分丰富。
潘素娟等人[1]分别介绍了参数假设检验和非参数假设检验两种方法,并通过案例分析了假设检验理论的应用,对抽样的数据进行推断分析,为以后的实际应用提供理论依据。
缪海斌和周炳海[2]在对具体案例进行研究时发现,制造产品过程中的问题,可以引用假设检验来进行测试,从而以最短的时间找到解决的办法。
从产品在生产过程中的众多输入因素中,选出问题存在的深层次原因。
对于原因的查找需要采用假设检验的方法展开统计,从而可以探知真正的问题所在,并使用实验设计等工业工程和六西格玛改善工具对根本原因进行改进,最终显著改善了产品的质量。
张淑贵[3]指出假设检验亦称显著性检验,是统计推断的重要内容。

假设检验-单样本检验假设检验时数据分析必须学习的⽅法第⼀部分:误差思维和置信区间什么是误差思维?误差永远存在、不可避免随机⼲扰因素的影响⼀个量在测量、计算或观察过程中由于某些错误或通常由于某些不可控制的因素的影响⽽造成的变化偏离标准值或规定值的数量,误差是不可避免的。
只要有估计,就会有误差。
什么是置信区间?置信区间:误差范围什么是置信⽔平?置信⽔平:区间包含总体平均值的概率p(a<样本平均值<b)=Y%这⾥选常⽤置信⽔平%95,即精度为2个标准误差范围内:通过游戏可视化理解置信区间?如何计算⼤样本的置信区间?⼤样本:当⼀个抽样调查的样本数量⼤于30。
这时候可以近似看出样本抽样分布趋近于正态分布,因此它符合中⼼极限定理。
下⾯以计算全国成年男性的平均⾝⾼为例,假设抽取样本100⼈,平均值167.1cm,标准差0.2cm 1.确定要求解的问题计算全国成年男性的平均⾝⾼范围及精度2.求样本的平均值和标准误差3.确定置信⽔平这⾥选常⽤置信⽔平%95,即精度为2个标准误差范围内:4.求出置信区间上下限的值(1)由于选⽤的样本⼤⼩为100⼤于30符合正态分布,先求出如下图中两块红⾊区域⾯积(概率):(2)通过查z表格查出标准分Z=-1.96(3)求出a和b的值的⽅法:(4)根据中⼼极限定理,样本平均值约等于总体平均值,最终求出a和b的值:结论:当我们选⽤置信⽔平为%95时,求得置信区间为[167.0608,167.1392],即在两个标准误差范围内,全国成年男性的平均⾝⾼为167.0608cm到167.1392cm之间。
5.常⽤置信⽔平及其对应Z值(标准分)如何计算⼩样本的置信区间?⼩样本:当⼀个抽样调查的样本数量⼩于30。
这时候抽样分布符合t分布:在概率论和统计学中,t-分布(t-distribution)⽤于根据⼩样本来估计呈正态分布且⽅差未知的总体的均值。
如果总体⽅差已知(例如在样本数量⾜够多时),则应该⽤正态分布来估计总体均值。
第12章分布类型的检验本章将涉及统计学分析中最为主要的理论之一:假设检验,它是分析统计数据、构建统计模型进行决策支持的基石。
12.1假设检验的基本思想12.1.1问题的提出12.1.2假设检验的基本步骤1.小概率事件在讨论假设检验的基本思想之前,首先需要明确小概率事件这一概念。
衡量一个事件发生与否可能性的标准是概率大小,通常概率大的事件容易发生,概率小的事件不容易发生。
习惯上将发生概率很小,如P<=0.05的事件称为小概率事件,表示在一次实验或观察中该事件发生的可能性很小,因此,如果只进行一次试验,可以视为不会发生。
这里需要澄清一个事实:注意上面的表述是“一次试验中小概率事件不应当发生”,这并不表示小概率事件不可能发生,也就是说,这里有一个前提:只进行一次试验,结果应当不会是小概率事件。
如果进行多次(可能无穷多)试验,那么小概率事件就肯定会发生,或者说,小概率事件在一次试验中不大可能发生,然而在大量试验中几乎是必然发生的。
2.小概率反证法假设检验的基本思想是统计学的“小概率反证法”原理:对于一个小概率事件而言,其对立面发生的可能性显然要大大高于这一小概率事件,可以认为,小概率事件在一次试验中不应当发生。
因此可以首先假定需要考察的假设是成立的,然后基于此进行推导,来计算一下在该假设所代表的总体中进行抽样研究得到当前样本(及更极端样本)的概率是多少。
如果结果显示这是一个小概率事件,则意味着如果假设是成立的,则在一次抽样研究中竟然就发生了小概率事件!这显然违反了小概率原理,因此可以按照反证法的思路推翻所给出的假设,认为它们实际上是不成立的,这就是小概率反证法原理。
假设检验的基本逻辑:先成立一个与H1相对立的H0。
各种假设检验方法都是根据H0来成立抽样分布,然后求出H0是正确的可能性。
如果我们能证明H0是对的可能性很小,那么就可以据此排除抽样误差的说法,认为H1可能是对的。
简言之,假设检验的基本原则是直接检验H0因而间接地检验H1,目的是排除抽样误差的可能性。
案例一:假设检验设备判断中的应用[1]
例如:某公司想从国外引进一种自动加工装置。
这种装置的工作温度X服从正态分布(μ,52),厂方说它的平均工作温度是80度。
从该装置试运转中随机测试16次,得到的平均工作温度是83度。
该公司考虑,样本结果与厂方所说的是否有显著差异?厂方的说法是否可以接受?
类似这种根据样本观测值来判断一个有关总体的假设是否成立的问题,就是假设检验的问题。
我们把任一关于单体分布的假设,统称为统计假设,简称假设。
上例中,可以提出两个假设:一个称为原假设或零假设,记为H0:μ=80(度);另一个称为备择假设或对立假设,记为H1 :μ≠80(度)这样,上述假设检验问题可以表示为:
H0:μ=80H1:μ≠80
原假设与备择假设相互对立,两者有且只有一个正确,备择假设的含义是,一旦否定原假设H0,备择假设H1备你选择。
所谓假设检验问题就是要判断原假设H0是否正确,决定接受还是拒绝原假设,若拒绝原假设,就接受备择假设。
应该如何作出判断呢?如果样本测定的结果是100度甚至更高(或很低),我们从直观上能感到原假设可疑而否定它,因为原假设是真实时,在一次试验中出现了与80度相距甚远的小概率事件几乎是不可能的,而现在竟然出现了,当然要拒绝原假设H0。
现在的问题是样本平均工作温度为83度,结果虽然与厂方说的80度有差异,但样本具有随机性,80度与83度之间的差异很可能是样本的随机性造成的。
在这种情况下,要对原假设作出接受还是拒绝的抉择,就
必须根据研究的问题和决策条件,对样本值与原假设的差异进行分析。
若有充分理由认为这种差异并非是由偶然的随机因素造成的,也即认为差异是显著的,才能拒绝原假设,否则就不能拒绝原假设。
假设检验实质上是对原假设是否正确进行检验,因此,检验过程中要使原假设得到维护,使之不轻易被否定,否定原假设必须有充分的理由;同时,当原假设被接受时,也只能认为否定它的根据不充分,而不是认为它绝对正确。
[编辑]
案例二:假设检验在卷烟质量判断中的应用[2]
在卷烟生产企业经常会遇到如下的问题:卷烟检验标准中要求烟支的某项缺陷的不合格品率P不能超过3%,现从一批产品中随机抽取50支卷烟进行检验,发现有2支不合格品,问此批产品能否放行?按照一般的习惯性思维:50支中有2支不合格品,不合格品率就是4%,超过了原来设置的3%的不合格品率,因此不能放行。
但如果根据假设检验的理论,在α=0.05的显著性水平下,该批产品应该可以放行。
这是为什么呢?
最关键的是由于我们是在一批产品中进行抽样检验,用抽样样本的质量水平来判别整批的质量水平,这里就有一个抽样风险的问题。
举例来说,我们的这批产品共有10000支卷烟,里面有4支不合格品,不合格品率是0.04%,远低于3%的合格放行不合格品率。
但我们的检验要求是随机抽样50支,用这50支的质量水平来判别整批10000支的质量水平。
如果在50支中恰好抽到了2支甚至更多的不合格品,简单地用抽到的不合格品数除以50来作为不合格品率来判断,那我们就会对这批质量水平合格的产品进行误判。
如何科学地进行判断呢?这就要用到假设检验的理论。
步骤1:建立假设
要检验的假设是不合格品率P是否不超过3%,因此立假设
H0:P≤0.03
这是原假设,其意是:与检验标准一致。
H1:P>0.03
步骤2:选择检验统计量,给出拒绝域的形式
若把比例P看作n=1的二项分别b(1,p)中成功的概率,则可在大样本场合(一般n≥25)获得参数p的近似μ的检验,可得样本统计量:近似服从N(0,1) 其中=2/50=0.04,p=0.03,n=50
步骤3:给出显著性水平α,常取α=0.05。
步骤4:定出临界值,写出拒绝域W。
根据α=0.05及备择假设知道拒绝域W为
步骤5:由样本观测值,求得样本统计量,并判断。
结论:在α=0.05时,样本观测值未落在拒绝域,所以不能拒绝原假设,应允许这批产品出厂。
假设检验中的两类错误。
进一步研究一下这个例子,在50个样品中抽到多少个不合格品,就要拒绝入库呢?我们仍取α=0.05,根据上述公式,得出,解得x>3.48,也就是在50个样品中抽到4个不合格品才能判整批为不合格。
而如果我们改变α的取值,也就是我们定义的小概率的取值,比如说取α=0.01,认为概率不超过0.01的事件发生了就是不合理的了,那又会怎样呢?还是用上面的公式计算,则得出,解得x>4.30,也就是在50个样品中抽到5个不合格品才能判整批为不合格。
检验要求是不合格品率P不能超过3%,而现在根据α=0.01,算出来50个样品中抽到5个不合格品才能判整批为不合格,会不会犯错误啊!假设检验是根据样本的情况作的统计推断,是推断就会犯错误,我们的任务是控制犯错误的概率。
在假设检验中,错误有两类:
第一类错误(拒真错误):原假设H0为真(批产品质量是合格的),但由于抽样的随机性(抽到过多的不合格品),样本落在拒绝域W内,从而导致拒绝H0(根据样本的情况把批质量判断为不合格)。
其发生的概率记为α,也就是显著性水平。
α控制的其实是生产方的风险,控制的是生产方所承担的批质量合格而不被接受的风险。
第二类错误(取伪错误):原假设H0不真(批产品质量是不合格的),但由于抽样的随机性(抽到过少的不合格品),样本落在W外,从而导致接受
H0(根据样本的情况把批质量判断为合格)。
其发生的概率记为β。
β控制的其实是使用方的风险,控制的是使用方所承担的接受质量不合格批的风险。
再回到刚刚计算的上例的情况,α由0.05变化为0.01,我们对批质量不合格的判断由50 个样本中出现4个不合格变化为5个,批质量是合格的而不被接受的风险就小了,犯第一类错误的风险小了,也就是生产方的风险小了;但同时随着α的减小对批质量不合格的判断条件其实放宽了——50个样本中出现4个不合格变化为5个,批质量是不合格的而被接受的风险大了;犯第二类错误的风险大了,也就是使用方的风险大了。
在相同样本量下,要使α小,必导致β大;要使β小,必导致α大,要同时兼顾生产方和使用方的风险是不可能的。
要使α、β皆小,只有增大样本量,这又增加了质量成本。
因此综上所述,假设检验可以告诉我们如何科学地进行质量合格判定,又告诉我们要兼顾生产方和使用方的质量风险,同时考虑质量和成本的问题。
如有侵权请联系告知删除,感谢你们的配合!。