异步电机dq坐标系上的数学模型推导

异步电机控制算法基础异步电机，又称感应电机，是工业应用中最常见的电动机类型之一。

它的运行不依赖于外部的同步信号，而是通过内部的电磁感应产生转矩。

由于其结构简单、维护成本低以及可靠性高等特点，异步电机在诸多领域，如制造业、风力发电、水泵系统等都发挥着重要的作用。

随着电力电子技术、微处理器技术和控制理论的发展，异步电机的控制算法也日益丰富和精确。

本文将详细探讨异步电机控制算法的基础理论，包括数学模型、控制策略及其在实际系统中的应用。

一、异步电机的基本数学模型理解异步电机的控制算法，首先要从其数学模型入手。

异步电机的数学模型相对复杂，但可以通过合理的简化和假设来降低其复杂性。

常用的数学模型有dq轴模型、αβ轴模型以及基于这些模型的派生模型。

1. dq轴模型dq轴模型是通过Park变换将三相异步电机的电压、电流和磁链等物理量从静止的abc坐标系转换到旋转的dq坐标系中。

在dq坐标系下，电机的电压方程、磁链方程和转矩方程可以表示为相对简单的形式，便于分析和设计控制器。

2. αβ轴模型αβ轴模型是通过Clarke变换将三相异步电机的物理量从abc坐标系转换到两相正交的αβ坐标系中。

这种模型在分析和设计某些类型的控制器（如直接转矩控制）时特别有用。

二、异步电机的控制策略异步电机的控制策略主要可以分为两大类：矢量控制（也称为场向量控制）和直接转矩控制。

1. 矢量控制矢量控制是一种高性能的异步电机控制策略，它通过模拟直流电机的控制方式来独立控制异步电机的转矩和磁通。

矢量控制的核心思想是通过坐标变换将异步电机的定子电流分解为产生磁通的励磁分量和产生转矩的转矩分量，然后分别对这两个分量进行控制。

通过这种方式，矢量控制可以实现异步电机的高性能调速，包括快速的动态响应、高精度的速度控制和宽广的调速范围。

2. 直接转矩控制直接转矩控制是一种直接控制异步电机电磁转矩的控制策略。

它不需要进行复杂的坐标变换，而是直接在定子坐标系下计算和控制电机的转矩。

dq坐标系数学模型引言：dq坐标系是一种常用的坐标系，广泛应用于数学模型中。

本文将介绍dq坐标系的基本概念、转换公式以及在数学模型中的应用。

一、dq坐标系的基本概念dq坐标系是一种以dq轴为基础的坐标系，其中d轴表示直流分量，q轴表示交流分量。

在dq坐标系中，任意向量可以表示为d轴和q 轴的线性组合，即：Vd = V * cos(θ)Vq = V * sin(θ)其中V为向量的幅值，θ为向量的角度。

二、dq坐标系的转换公式在dq坐标系中，向量的转换可以通过dq坐标系的变换公式来实现。

dq坐标系的转换公式如下：Vα = Vd * cos(θ) - Vq * sin(θ)Vβ = Vd * sin(θ) + Vq * cos(θ)其中Vα和Vβ为向量在α轴和β轴上的分量，θ为dq坐标系与αβ坐标系之间的夹角。

三、dq坐标系在数学模型中的应用1. 电力系统中的dq坐标系dq坐标系在电力系统中广泛应用于电压和电流的分析和控制。

通过dq坐标系的转换，可以将电压和电流从三相坐标系转换到dq坐标系，简化了电力系统的分析和控制过程。

2. 电机控制中的dq坐标系dq坐标系也被广泛应用于电机控制领域。

通过dq坐标系的转换，可以将电机的电流从三相坐标系转换到dq坐标系，实现对电机的精确控制。

3. 电力电子领域中的dq坐标系dq坐标系在电力电子领域中也有重要的应用。

通过dq坐标系的转换，可以对电力电子器件的电流进行精确控制，提高电力电子系统的效率和稳定性。

4. 机器人控制中的dq坐标系dq坐标系在机器人控制中也有广泛的应用。

通过dq坐标系的转换，可以将机器人的位姿从笛卡尔坐标系转换到dq坐标系，实现对机器人的精确控制。

结论：dq坐标系是一种常用的坐标系，广泛应用于数学模型中。

本文介绍了dq坐标系的基本概念、转换公式以及在数学模型中的应用。

dq 坐标系的应用领域广泛，包括电力系统、电机控制、电力电子和机器人控制等。

通过dq坐标系的转换，可以简化数学模型的分析和控制过程，提高系统的效率和稳定性。

6.５异步电动机的动态数学模型和坐标变换本节提要ﻫ异步电动机动态数学模型的性质三相异步电动机的多变量非线性数学模型坐标变换和变换矩阵三相异步电动机在两相坐标系上的数学模型ﻫ三相异步电动机在两相坐标系上的状态方程ﻫ一、异步电动机动态数学模型的性质2. 交流电机数学模型的性质(1）异步电机变压变频调速时需要进行电压(或电流)和频率的协调控制,有电压(电流）和频率两种独立的输入变量。

在输出变量中，除转速外，磁通也得算一个独立的输出变量。

因为电机只有一个三相输入电源，磁通的建立和转速的变化是同时进行的,为了获得良好的动态性能,也希望对磁通施加某种控制，使它在动态过程中尽量保持恒定,才能产生较大的动态转矩。

ﻫ多变量、强耦合的模型结构由于这些原因,异步电机是一个多变量(多输入多输出)系统,而电压（电流)、频率、磁通、转速之间又互相都有影响,所以是强耦合的多变量系统,可以先用图来定性地表示。

图６-43 异步电机的多变量、强耦合模型结构模型的非线性(2)在异步电机中,电流乘磁通产生转矩,转速乘磁通得到感应电动势,由于它们都是同时变化的，在数学模型中就含有两个变量的乘积项。

这样一来,即使不考虑磁饱和等因素，数学模型也是非线性的。

模型的高阶性ﻫ（３)三相异步电机定子有三个绕组，转子也可等效为三个绕组,每个绕组产生磁通时都有自己的电磁惯性,再算上运动系统的机电惯性,和转速与转角的积分关系，即使不考虑变频装置的滞后因素，也是一个八阶系统。

ﻫ总起来说，异步电机的动态数学模型是一个高阶、非线性、强耦合的多变量系统。

ﻫ二、三相异步电动机的多变量非线性数学模型假设条件：ﻫ (1)忽略空间谐波，设三相绕组对称，在空间互差１20°电角度，所产生的磁动势沿气隙周围按正弦规律分布；(2）忽略磁路饱和,各绕组的自感和互感都是恒定的;(３)忽略铁心损耗；ﻫ (4)不考虑频率变化和温度变化对绕组电阻的影响。

1. 电压方程三相定子绕组的电压平衡方程为 :电压方程(续)与此相应，三相转子绕组折算到定子侧后的电压方程为:电压方程的矩阵形式将电压方程写成矩阵形式，并以微分算子 p 代替微分符号ｄ /dt或写成(6-67ｂ）2. 磁链方程每个绕组的磁链是它本身的自感磁链和其它绕组对它的互感磁链之和，因此，六个绕组的磁链可表达为：或写成（6-68ｂ)电感矩阵式中，Ｌ是6×６电感矩阵，其中对角线元素ＬAA, ＬBＢ， LCＣ,Laａ,Lbb,Lcｃ是各有关绕组的自感,其余各项则是绕组间的互感。

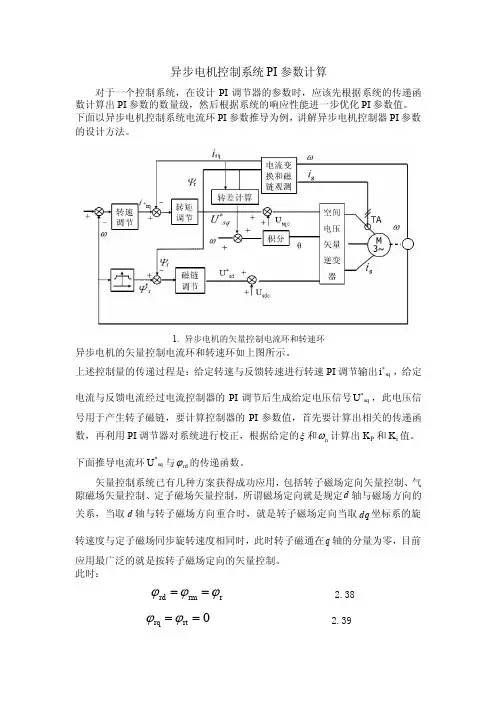
异步电机控制系统PI 参数计算对于一个控制系统，在设计PI 调节器的参数时，应该先根据系统的传递函数计算出PI 参数的数量级，然后根据系统的响应性能进一步优化PI 参数值。

下面以异步电机控制系统电流环PI 参数推导为例，讲解异步电机控制器PI 参数的设计方法。

1. 异步电机的矢量控制电流环和转速环异步电机的矢量控制电流环和转速环如上图所示。

上述控制量的传递过程是：给定转速与反馈转速进行转速PI 调节输出sq *i ，给定电流与反馈电流经过电流控制器的PI 调节后生成给定电压信号sq *U ，此电压信号用于产生转子磁链，要计算控制器的PI 参数值，首先要计算出相关的传递函数，再利用PI 调节器对系统进行校正，根据给定的ξ和n ω计算出K P 和K i 值。

下面推导电流环sq *U 与rd ϕ的传递函数。

矢量控制系统已有几种方案获得成功应用，包括转子磁场定向矢量控制、气隙磁场矢量控制、定子磁场矢量控制，所谓磁场定向就是规定d 轴与磁场方向的关系，当取d 轴与转子磁场方向重合时，就是转子磁场定向当取dq 坐标系的旋转速度与定子磁场同步旋转速度相同时，此时转子磁通在q 轴的分量为零，目前应用最广泛的就是按转子磁场定向的矢量控制。

此时：r rm rd ϕϕϕ== 2.38 0rt rq ==ϕϕ 2.39ωωω-=1s 2.40磁链方程：rd m sd s i L i L +=sdϕrq m sq s i L i L +=sq ϕ 2.41rd r sd m i L i L +=rd ϕ 0sq =+=rq r sq m i L i L ϕ由以上四式解出rd i 、rq i 与sd i 、sq i 的关系：rsq m rq L i L i -= 2.42)(1sd m rd rrd i L L i -=ϕ 2.43根据文件上《异步电机dq 坐标系上的数学模型推导》得出：sq dqs sd sd s sd P i R u ϕωϕ-+=sd dqs sq sq s sq P i R u ϕωϕ-+=0=+=rd rd r rd P i R u ϕ 2.440=+=rd dqr rq r rq i R u ϕω在鼠笼式异步电机中rd u 、rq u 为0。

6.5 异步电动机的动态数学模型和坐标变换本节提要异步电动机动态数学模型的性质三相异步电动机的多变量非线性数学模型坐标变换和变换矩阵三相异步电动机在两相坐标系上的数学模型三相异步电动机在两相坐标系上的状态方程一、异步电动机动态数学模型的性质2. 交流电机数学模型的性质（1）异步电机变压变频调速时需要进行电压（或电流）和频率的协调控制，有电压（电流）和频率两种独立的输入变量。

在输出变量中，除转速外，磁通也得算一个独立的输出变量。

因为电机只有一个三相输入电源，磁通的建立和转速的变化是同时进行的，为了获得良好的动态性能，也希望对磁通施加某种控制，使它在动态过程中尽量保持恒定，才能产生较大的动态转矩。

多变量、强耦合的模型结构由于这些原因，异步电机是一个多变量（多输入多输出）系统，而电压（电流）、频率、磁通、转速之间又互相都有影响，所以是强耦合的多变量系统，可以先用图来定性地表示。

图6-43 异步电机的多变量、强耦合模型结构模型的非线性（2）在异步电机中，电流乘磁通产生转矩，转速乘磁通得到感应电动势，由于它们都是同时变化的，在数学模型中就含有两个变量的乘积项。

这样一来，即使不考虑磁饱和等因素，数学模型也是非线性的。

模型的高阶性（3）三相异步电机定子有三个绕组，转子也可等效为三个绕组，每个绕组产生磁通时都有自己的电磁惯性，再算上运动系统的机电惯性，和转速与转角的积分关系，即使不考虑变频装置的滞后因素，也是一个八阶系统。

总起来说，异步电机的动态数学模型是一个高阶、非线性、强耦合的多变量系统。

二、三相异步电动机的多变量非线性数学模型假设条件：（1）忽略空间谐波，设三相绕组对称，在空间互差120°电角度，所产生的磁动势沿气隙周围按正弦规律分布；（2）忽略磁路饱和，各绕组的自感和互感都是恒定的；（3）忽略铁心损耗；（4）不考虑频率变化和温度变化对绕组电阻的影响。

1. 电压方程三相定子绕组的电压平衡方程为：电压方程（续）与此相应，三相转子绕组折算到定子侧后的电压方程为：电压方程的矩阵形式将电压方程写成矩阵形式，并以微分算子 p 代替微分符号 d /dt或写成（6-67b）2. 磁链方程每个绕组的磁链是它本身的自感磁链和其它绕组对它的互感磁链之和，因此，六个绕组的磁链可表达为：或写成（6-68b）电感矩阵式中，L 是6×6电感矩阵，其中对角线元素 LAA， LBB， LCC，Laa，Lbb，Lcc 是各有关绕组的自感，其余各项则是绕组间的互感。

异步电动机动态数学模型
异步电动机是目前应用最广泛的电机之一，它在各种工业和民用
领域中扮演着重要角色。

为了更好地控制异步电动机的运转，需要对
其进行动态数学模型建立。

异步电动机动态数学模型主要有两种，分别为转子定子“dq”坐
标模型和矢量控制模型。

下面针对这两种模型来进行详细介绍。

转子定子“dq”坐标模型是一种传统的动态数学模型，它通过转
子电流和定子电压的之间的相互作用来描述异步电动机的运转。

该模
型采用dq坐标系来描述电机转子和定子磁电量的动态变化规律。

在该
模型中，异步电动机的动态方程由Vdq、Idq、ω、ψd、ψq等变量的
微分方程组成，其中Vdq为定子dq坐标系瞬时电压，Idq为定子dq坐标系电流，ω为转子机械角速度，ψd和ψq分别为定子dq坐标系磁链。

矢量控制模型是一种比较新的动态数学模型，它采用磁场定向原
理来描述异步电动机的运转。

该模型通过电机磁链的矢量控制来实现
对电机的动态控制。

在该模型中，磁链矢量控制可以通过控制电机空
间矢量波的角度和大小来实现。

该模型可以使用Park变换和Clarke
变换将电机三相坐标系转换为dq坐标系，进而通过PI控制算法实现
对电机的动态控制。

总体来说，异步电动机动态数学模型可以帮助我们更好地掌握异
步电动机的运转规律，为实际控制提供指导意义。

无论采用哪种模型，
都需要进行模型参数的识别和校正，并根据具体情况确定控制策略，才能更好地实现对异步电动机的控制。

异步电机的数学模型是一个高阶、非线性、强耦合的多变量系统[1]。

在研究异步电机的多变量数学模型时，常作如下假设：(1)三相绕组在空间对称互差 120，磁势在空间按正弦分布； (2)忽略铁芯损耗；(3)不考虑磁路饱和，即认为各绕组间互感和自感都是线性的； (4)不考虑温度和频率变化对电机参数的影响。

异步电机在两相静止坐标系上的数学模型：仿真的基本思想是利用物理的或数学的模型来类比模仿现实过程，以寻求过程和规律。

在实际过程中，系统可能太复杂，无法求得其解析解，可以通过仿真求得其数值解。

计算机仿真是利用计算机对所研究系统的结构、功能和行为以及参与系统控制的主动者——人的思维过程和行为，进行动态性的比较和模仿，利用建立的仿真模型对系统进行研究和分析，并可将系统过程演示出来。

系统仿真软件MATLAB 不但在数值计算和符号计算方面具有强大的功能，而且在计算结果的分析和数据可视化方面有着其他类似软件难以匹敌的优势。

界面友好，编程效率高，扩展性强。

MATLAB 提供的SIMULINK 是一个用来对动态系统进行建模、仿真和分析的软件包。

SIMULINK 的目的是让用户能够把更多的精力投入到模型设计本身。

它提供了一些基本的模块，这些模块放在浏览器里面，用户可以随时调用。

当模型构造之后，用户可以进行仿真，等待结果，或者改变参数，再进行仿真。

异步电机的动态数学模型是一个高阶、非线性、强耦合的多变量系统，其动态和静态特性都相当复杂。

以下将介绍用SIMULINK 如何来建立三相异步电机的计算机仿真模型，为以后的系统仿真做好准备。

经过三相静止/两相静止坐标变换及两相旋转/两相静止坐标变换，可得异步电机在两相静止坐标系上的数学模型。

电压方程：⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--+++=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡βαβαβαβαωωωωr r s s r r r m m r r r r m r m m S m S r r s s i i i i P L R L P L L L P L R L P L P L P L R P L P L R u u u u 22110000磁链方程：⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡βαβαβαβαψψψψr r s s r mr m m sm s r r s s i i i i L L L L L L L L 0000000转矩方程：[])(0110βααββαβαr s r s m p r r s s m p e i i i i L n i i i i L n T -=⎥⎦⎤⎢⎣⎡⋅⎥⎦⎤⎢⎣⎡-⋅= 转速方程：L e rp T T dt d n J -=ω式中： m m L L 123=—οβα、、静止坐标系上定子与转子绕组间的互感，m s s L L L 123+=σ—οβα、、静止坐标系上两相定子绕组的自感，m r r L L L 123+=σ—οβα、、静止坐标系上两相转子绕组的自感，1R 、2R —定、转子电阻，L T 为负载阻转矩，J 为机组的转动惯量，p n 极对数，r ω为电机转子的旋转角速度。

异步电机在两相静止坐标系上的数学模型：经过三相静止/两相静止坐标变换及两相旋转/两相静止坐标变换，可得异步电机在两相静止坐标系上的数学模型。

电压方程：⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--+++=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡βαβαβαβαωωωωr r s s r rr m mr r r r mr m m S m S r r s s i i ii P L R L PL L L P L R L P L PL PL R P L PL R u u u u 2211000 （3.1.5）磁链方程：⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡βαβαβαβαψψψψr r s s r mr m m s m sr r s s i i i i L L L L L L L L 0000000 （3.1.6）转矩方程：[])(0110βααββαβαr s r s m p r r s s m p e i i i i L n i i i i L n T -=⎥⎦⎤⎢⎣⎡⋅⎥⎦⎤⎢⎣⎡-⋅= （3.1.7） 转速方程：L e r pT T dtd n J -=ω （3.1.8）式中： mm L L 123=—οβα、、静止坐标系上定子与转子绕组间的互感，ms s L L L 123+=σ—οβα、、静止坐标系上两相定子绕组的自感，m r r L L L 123+=σ—οβα、、静止坐标系上两相转子绕组的自感，1R 、2R —定、转子电阻，L T 为负载阻转矩，J 为机组的转动惯量，p n 极对数，r ω为电机转子的旋转角速度。

在进行交流传动控制系统仿真时，第一步必须建立异步电动机的仿真模型。

为了使仿真结果尽可能地接近异步电动机的实际运行状况，仿真模型应该与异步电动机的原始模型尽量保持一致，在这种情况下，所得到的仿真结果才具有现实指导意义。

在这里，以两相静止οβα、、坐标系中的数学模型作为建立仿真模型的依据，该数学模型是在变换前后功率保持不变的约束条件下，经过三相静止到两相静止坐标变换得到的，不需要其他假设条件。