伺服电机的选型及应用案例介绍
- 格式:pptx
- 大小:7.85 MB
- 文档页数:30


伺服电机的选型计算及应用案例介绍伺服电机是一种能够精确控制转速和位置的电动机,广泛应用于工业自动化领域。
选型计算是确定伺服电机规格和性能的过程,通常涉及到转矩、转速、功率、惯量等参数的综合考虑。
1.确定负载要求:首先需要明确伺服电机所驱动的负载的要求,包括所需转矩、转速和精度等。
2.计算转矩需求:根据负载要求,可以通过转矩计算公式来估算所需的转矩。
常用的转矩计算公式为:转矩=负载惯量x加速度角加速度+负载转矩其中,负载惯量是指负载的惯性矩,加速度角加速度是指负载加速度的转矩。
3.计算转速需求:根据负载要求,可以通过转速计算公式来估算所需的转速。
常用的转速计算公式为:转速=转矩/转矩常数其中,转矩常数是伺服电机的特性参数,代表单位转矩所需要的电压或电流。
4.确定功率需求:根据转矩和转速需求,可以计算出所需的功率。
功率可以通过转速和转矩的乘积来计算。
功率=转矩x转速5.确定惯量需求:根据负载的惯性矩和转矩需求,可以计算出所需的惯性矩。
惯性矩可以通过负载的质量和尺寸来计算。
以上是伺服电机选型计算的基本步骤,具体的选型还需要考虑其他因素,如环境温度、耐用性、可靠性等。
下面以一个应用案例来介绍伺服电机的选型计算。
假设有一个机械臂需要驱动,臂长为1米,质量为10千克。
机械臂需要能够承受10牛米的转矩,并以每分钟100转的速度旋转。
根据这些要求,可以使用以下公式计算伺服电机的规格和性能。
负载惯量=质量x(臂长^2)转矩需求=负载惯量x加速度角加速度+负载转矩加速度角加速度=转速/时间转速=100转/分钟负载转矩=10牛米根据以上参数,可以计算出负载惯量、加速度角加速度、转矩需求等。
假设加速时间为1秒,则有:加速度角加速度=(100转/分钟)/(60秒/分钟)/(1秒)=1.67转/秒^2负载惯量=10千克x(1米^2)=10千克·米^2转矩需求=10千克·米^2x(1.67转/秒^2)+10牛米=26.7牛米根据转矩需求和伺服电机的特性参数,可以选择合适的伺服电机。
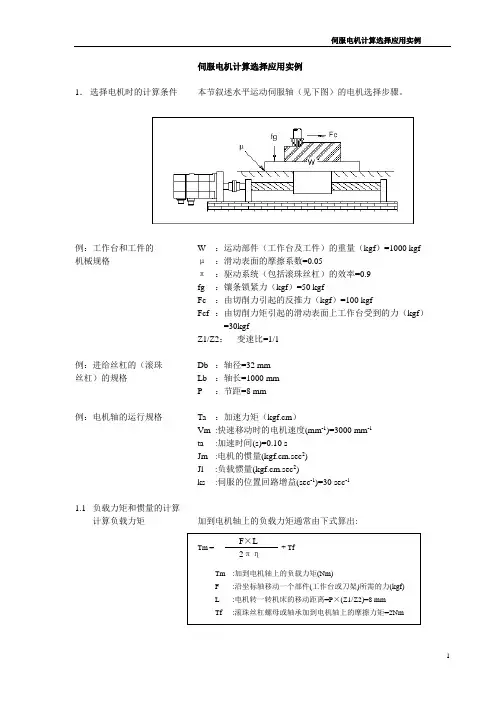
伺服电机计算选择应用实例1. 选择电机时的计算条件 本节叙述水平运动伺服轴(见下图)的电机选择步骤。
例:工作台和工件的W :运动部件(工作台及工件)的重量(kgf )=1000 kgf 机械规格 μ :滑动表面的摩擦系数=0.05π :驱动系统(包括滚珠丝杠)的效率=0.9 fg :镶条锁紧力(kgf )=50 kgfFc :由切削力引起的反推力(kgf )=100 kgfFcf:由切削力矩引起的滑动表面上工作台受到的力(kgf ) =30kgfZ1/Z2: 变速比=1/1例:进给丝杠的(滚珠 Db :轴径=32 mm 丝杠)的规格 Lb :轴长=1000 mm P :节距=8 mm例:电机轴的运行规格 Ta :加速力矩(kgf.cm )Vm :快速移动时的电机速度(mm -1)=3000 mm -1 ta :加速时间(s)=0.10 sJm :电机的惯量(kgf.cm.sec 2) Jl :负载惯量(kgf.cm.sec 2)ks :伺服的位置回路增益(sec -1)=30 sec -11.1 负载力矩和惯量的计算 计算负载力矩 加到电机轴上的负载力矩通常由下式算出:Tm = + Tf Tm :加到电机轴上的负载力矩(Nm) F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf) L :电机转一转机床的移动距离=P ×(Z1/Z2)=8 mmTf:滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2NmF ×L2πη无论是否在切削,是垂直轴还是水平轴,F值取决于工作台的重量,摩擦系数。
若坐标轴是垂直轴,F值还与平衡锤有关。
对于水平工作台,F值可按下列公式计算:不切削时:F = μ(W+fg)例如:F=0.05×(1000+50)=52.5 (kgf)Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf)例如:F=100+0.05×(1000+50+30)=154(kgf)Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1,应根据数据单选择电机,其负载力矩在不切削时应大于0.9(Nm),最高转速应高于3000(min-1)。

伺服电机选型计算实例伺服电机是一种控制器控制的电机,具有高精度和高速度的特点,广泛应用于机械设备中。
在选型伺服电机时,需要考虑多个参数来满足具体的应用要求。
下面以一个选型计算实例来详细介绍伺服电机的选型过程。
假设我们需要选型一台伺服电机用于驱动一个线传动机构,具体要求如下:1.最大负载力为2000N,工作速度范围为0-10m/s。
2. 线传动机构的负载惯量为500kg·m²。
3. 需要保证驱动精度在±0.2mm范围内。
4.工作环境温度范围为0-40℃。
首先,我们需要计算所需的转矩。
根据公式:转矩=负载力×工作半径,其中工作半径等于线传动机构的负载惯量÷2、由于我们没有具体的线传动机构参数,假设负载惯量为500kg·m²,即工作半径为0.25m。
则最大转矩=2000N×0.25m=500N·m。
考虑到一般情况下,峰值转矩为最大转矩的2倍,即1000N·m。
接下来,我们需要计算伺服电机的速度要求。
根据给定的工作速度范围0-10m/s,我们可以选择合适的额定转速。
假设我们选择的额定转速为2000rpm,则转速范围为0-2000rpm。
考虑到加速度和减速度的要求,一般额定转速的选择会略高于平均线速度,假设为2200rpm。
接下来,我们需要选择合适的伺服电机型号。
在选型之前,我们还需要考虑工作环境的温度范围。
根据给定的工作环境温度范围为0-40℃,我们需要选择具备合适温度范围的伺服电机。
一般伺服电机的温度范围为0-50℃,因此我们可以选择标准型号的伺服电机。
在选择伺服电机型号时,我们需要参考厂家提供的电机性能参数。
主要包括额定转矩、额定转速、额定电压、额定电流、额定功率等。
根据我们的要求,我们可以对比不同型号的伺服电机并选择合适的型号。
最后,我们需要根据具体应用需求考虑伺服电机的控制方式、接口类型以及其他附件等。
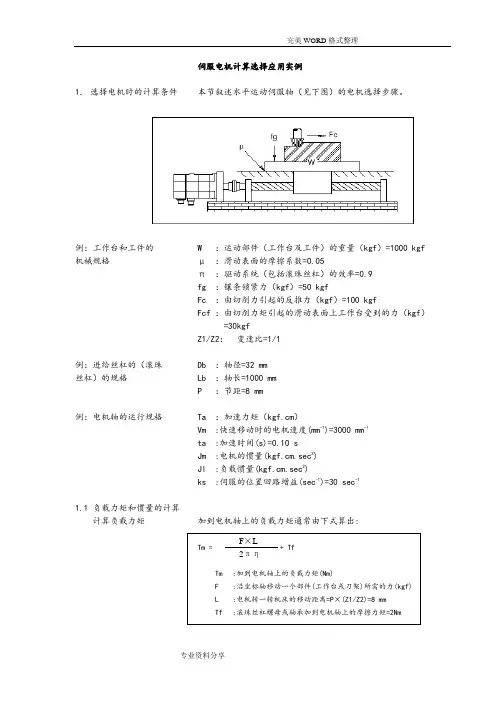
伺服电机计算选择应用实例1. 选择电机时的计算条件 本节叙述水平运动伺服轴(见下图)的电机选择步骤。
例:工作台和工件的 W :运动部件(工作台及工件)的重量(kgf )=1000 kgf 机械规格 μ :滑动表面的摩擦系数=0.05π :驱动系统(包括滚珠丝杠)的效率=0.9 fg :镶条锁紧力(kgf )=50 kgfFc :由切削力引起的反推力(kgf )=100 kgfFcf :由切削力矩引起的滑动表面上工作台受到的力(kgf )=30kgfZ1/Z2: 变速比=1/1例:进给丝杠的(滚珠 Db :轴径=32 mm 丝杠)的规格 Lb :轴长=1000 mm P :节距=8 mm例:电机轴的运行规格 Ta :加速力矩(kgf.cm )Vm :快速移动时的电机速度(mm -1)=3000 mm -1ta :加速时间(s)=0.10 sJm :电机的惯量(kgf.cm.sec 2)Jl :负载惯量(kgf.cm.sec 2)ks:伺服的位置回路增益(sec -1)=30 sec-11.1 负载力矩和惯量的计算 计算负载力矩 加到电机轴上的负载力矩通常由下式算出:Tm = + Tf Tm :加到电机轴上的负载力矩(Nm) F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf) L:电机转一转机床的移动距离=P ×(Z1/Z2)=8 mmTf :滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2NmF ×L 2πη无论是否在切削,是垂直轴还是水平轴,F值取决于工作台的重量,摩擦系数。
若坐标轴是垂直轴,F值还与平衡锤有关。
对于水平工作台,F值可按下列公式计算:不切削时:F = μ(W+fg)例如:F=0.05×(1000+50)=52.5 (kgf)Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf)例如:F=100+0.05×(1000+50+30)=154(kgf)Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1,应根据数据单选择电机,其负载力矩在不切削时应大于0.9(Nm),最高转速应高于3000(min-1)。
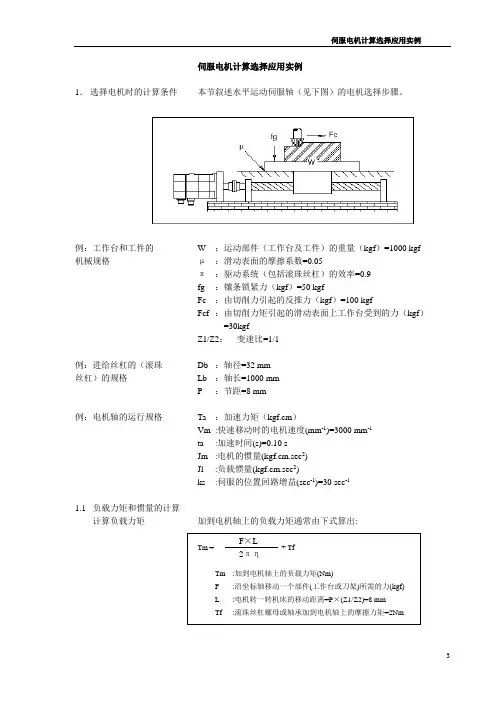
伺服电机计算选择应用实例1.选择电机时的计算条件本节叙述水平运动伺服轴(见下图)的电机选择步骤。
例:工作台和工件的W :运动部件(工作台及工件)的重量(kgf)=1000 kgf 机械规格μ:滑动表面的摩擦系数=0.05π:驱动系统(包括滚珠丝杠)的效率=0.9fg :镶条锁紧力(kgf)=50 kgfFc :由切削力引起的反推力(kgf)=100 kgfFcf :由切削力矩引起的滑动表面上工作台受到的力(kgf)=30kgfZ1/Z2:变速比=1/1例:进给丝杠的(滚珠Db :轴径=32 mm丝杠)的规格Lb :轴长=1000 mmP :节距=8 mm例:电机轴的运行规格Ta :加速力矩(kgf.cm)Vm :快速移动时的电机速度(mm-1)=3000 mm-1ta :加速时间(s)=0.10 sJm :电机的惯量(kgf.cm.sec2)Jl :负载惯量(kgf.cm.sec2)ks :伺服的位置回路增益(sec-1)=30 sec-11.1 负载力矩和惯量的计算计算负载力矩加到电机轴上的负载力矩通常由下式算出:Tm = + TfTm :加到电机轴上的负载力矩(Nm)F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf)L :电机转一转机床的移动距离=P×(Z1/Z2)=8 mmTf :滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2NmF×L2πη无论是否在切削,是垂直轴还是水平轴,F值取决于工作台的重量,摩擦系数。
若坐标轴是垂直轴,F值还与平衡锤有关。
对于水平工作台,F值可按下列公式计算:不切削时:F = μ(W+fg)例如:F=0.05×(1000+50)=52.5 (kgf)Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf)例如:F=100+0.05×(1000+50+30)=154(kgf)Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1,应根据数据单选择电机,其负载力矩在不切削时应大于0.9(Nm),最高转速应高于3000(min-1)。

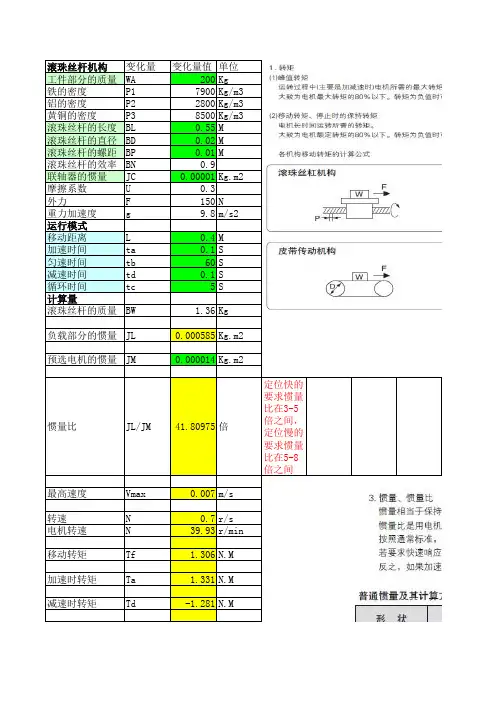
滚珠丝杆机构变化量变化量值单位工件部分的质量WA200Kg
铁的密度P17900Kg/m3铝的密度P22800Kg/m3黄铜的密度P38500Kg/m3滚珠丝杆的长度BL0.55M
滚珠丝杆的直径BD0.02M
滚珠丝杆的螺距BP0.01M
滚珠丝杆的效率BN0.9
联轴器的惯量JC0.00001Kg.m2摩擦系数U0.3
外力F150N
重力加速度g9.8m/s2运行模式
移动距离L0.4M
加速时间ta0.1S
匀速时间tb60S
减速时间td0.1S
循环时间tc5S
计算量
滚珠丝杆的质量BW 1.36Kg
负载部分的惯量JL0.000585Kg.m2预选电机的惯量JM0.000014Kg.m2
惯量比JL/JM41.80975倍定位快的要求惯量比在3-5倍之间,定位慢的要求惯量比在5-8倍之间
最高速度Vmax0.007m/s 转速N0.7r/s 电机转速N39.93r/min 移动转矩Tf 1.306N.M 加速时转矩Ta 1.331N.M 减速时转矩Td-1.281N.M
确认最大转矩Tmax N.M 加速时转矩=Ta
确认有效转矩Trms 4.531N.M。

伺服电机选型案例伺服电机功率计算选型例子伺服电机功率计算选型例子(新手必看,经典案例分析)伺服电机选型也有相应的规律和公式可循的。
最常见的机械传动结构有同步带,齿轮齿条,丝杆等。
以同步带为例,需要计算的参数有电机转速,电机力矩,转动惯量。
第一,电机额定转速N=(v/2πr)*i,启动瞬间需要的拉力F=(M+m1-m2)a+δ(M+m1-m2)g(水平),F=(M+m1-m2)a+δ(M+m1-m2)g+(M+m1-m2)g(垂直),T扭矩=F*R。
T电机=T扭矩/机械减速比n,电机功率=N*T 电机/10,启动惯量J=1/2mR2,电机惯量J电机=J/减速比的平方n2/惯量比i。
第二,同步带轮直径D=100mm、提升机载货台总重M=30kg、货物总重m1=10kg,配重m2=25kg,提升滚动摩擦系数取δ=0.03、加速度a=2m/S2、提升速度v=3m/s。
减速机减速比i=5,电机额定转速n=(v/2πr)*i=3/(2*3.14*0.05)*5*60=2866r/min,启动瞬间需要的拉力F=(M+m1-m2)a+&delta,(M+m1-m2)g+(M+m1-m2)g=(30+10-25)*2+0.03(30+10-25)*10+(30+10-25)*10=184.5N。
T扭矩=F*R=184.5*0.05=9.225Nm,折算电机需要扭矩T1=9.225Nm/5=1.85Nm,折算电机功率P1=2866*1.85/10=0.5KW。
启动惯量J=1/2mR2=0.5*(10+30+25)*0.0025=0.08125kgm2,折算电机需要惯量J1=0.08125/25=0.00325kgm2,根据经验值取惯量比=10,则实际J电=J1/10=0.000325kgm2。
经计算电机至少满足以下条件下面看下1.2千瓦3000RPM,4牛米的电机的惯量是2.98*10-4kgm2。
所以可以选择80ST-M04030的电机。


伺服电机选型计算实例在进行伺服电机选型时,需要考虑到多个因素,包括载荷特性、运动要求、控制要求以及环境要求等。
下面我们将通过一个实际案例来详细介绍伺服电机选型的计算方法。
案例描述:公司需要选购一台适合于自动化生产线上使用的伺服电机,用于驱动一台输送带,具体要求如下:1.输送带长度为2米,宽度为0.5米,预计最大负载为100千克。
2.需要实现起动、停止、加速和减速、定位等功能。
3.运动速度为1米/秒。
4.工作温度范围为-10℃~40℃。
根据以上要求,我们可以按照以下步骤进行伺服电机选型计算:步骤1:计算所需输出功率首先,我们需要计算伺服电机的输出功率。
根据输送带的长度、宽度和预计最大负载,可以计算得到输送带的质量:质量=长度×宽度×质量体积,质量体积可以通过相应材料的密度来获得。
假设输送带材料的密度为1克/立方厘米,则质量=2×0.5×1=1千克。
根据牛顿第二定律,质量乘以加速度等于力,所以我们可以得到加速度=质量/时间^2=100/1=100米/秒^2、再根据功率=力×速度,可以计算得到所需输出功率=力×速度=100×1=100瓦特。
步骤2:根据负载惯性计算电机惯性比为了实现加速和减速的控制要求,需要考虑负载的惯性。
负载的惯性通常用负载惯量来表示,通常使用kg*m^2作为单位。
对于输送带系统,我们假设负载的半径为0.25米(输送带宽度的一半),负载的惯量=负载质量×半径^2=100×0.25^2=6.25kg*m^2、然后,我们需要计算电机的惯性比,电机的惯量通常使用kg*m^2作为单位。
假设选用的伺服电机的惯量为0.01kg*m^2,则电机的惯性比=负载的惯量/电机的惯量=6.25/0.01=625步骤3:根据运动要求计算加速度和最大速度根据运动要求中的加速度和速度,我们可以计算得到实际需要的加速时间和加速距离。
伺服电机选型计算及案例
在进行伺服电机选型计算前,首先需要了解以下参数:
1.力矩要求:根据工作负载计算所需的最大输出力矩。
2.转速要求:根据工作过程中所需的最高转速确定。
3.加速度要求:根据工作过程中的速度变化率来计算。
4.环境条件:包括工作温度、工作湿度等环境因素。
下面以一个简单的案例为例,演示如何进行伺服电机选型计算。
案例:自动化生产线运行速度为60米/分钟,工作台上的工件质量为10千克,需要在0.5秒内从静止加速到最终速度并保持匀速运动。
根据这些要求,我们需要选用合适的伺服电机。
步骤1:计算所需的输出力矩。
根据牛顿第二定律,力矩(扭矩)等于质量乘以加速度。
加速度可以通过速度变化与时间的比值来计算。
加速度a = (60 m/min) / (0.5 s) = 120 m/min² = 2 m/s²
力矩T = (质量m) * (加速度a) = 10 kg * 2 m/s² = 20 Nm
所以我们需要选用至少能提供20Nm的输出力矩的伺服电机。
步骤2:计算所需的最高转速。
最高转速通常需要根据具体工作过程来确定。
在这个案例中,我们假设最高转速为3000 rpm(每分钟转数)。
步骤3:计算所需的加速度。
加速度已经在步骤1中计算过,为2m/s²。
步骤4:确定环境条件。
根据实际工作环境,确定伺服电机所需的环境参数,例如工作温度和湿度范围。
通过以上计算,我们得到了选型参数:输出力矩为20 Nm,最高转速为3000 rpm,加速度为2 m/s²。
伺服电机计算选择应用实例1. 选择电机时的计算条件 本节叙述水平运动伺服轴(见下图)的电机选择步骤。
例:工作台和工件的W :运动部件(工作台及工件)的重量(kgf )=1000 kgf 机械规格 μ :滑动表面的摩擦系数=0.05π :驱动系统(包括滚珠丝杠)的效率=0.9 fg :镶条锁紧力(kgf )=50 kgfFc :由切削力引起的反推力(kgf )=100 kgfFcf:由切削力矩引起的滑动表面上工作台受到的力(kgf ) =30kgfZ1/Z2: 变速比=1/1例:进给丝杠的(滚珠 Db :轴径=32 mm 丝杠)的规格 Lb :轴长=1000 mm P :节距=8 mm例:电机轴的运行规格 Ta :加速力矩(kgf.cm )Vm :快速移动时的电机速度(mm -1)=3000 mm -1 ta :加速时间(s)=0.10 sJm :电机的惯量(kgf.cm.sec 2) Jl :负载惯量(kgf.cm.sec 2)ks :伺服的位置回路增益(sec -1)=30 sec -11.1 负载力矩和惯量的计算 计算负载力矩 加到电机轴上的负载力矩通常由下式算出:Tm = + Tf Tm :加到电机轴上的负载力矩(Nm) F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf) L :电机转一转机床的移动距离=P ×(Z1/Z2)=8 mmTf:滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2NmF ×L2πη无论是否在切削,是垂直轴还是水平轴,F值取决于工作台的重量,摩擦系数。
若坐标轴是垂直轴,F值还与平衡锤有关。
对于水平工作台,F值可按下列公式计算:不切削时:F = μ(W+fg)例如:F=0.05×(1000+50)=52.5 (kgf)(52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)=Tm= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf)例如:F=100+0.05×(1000+50+30)=154(kgf)Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1,应根据数据单选择电机,其负载力矩在不切削时应大于0.9(Nm),最高转速应高于3000(min-1)。
第1篇一、引言伺服电机作为一种高精度、高性能的电动机,广泛应用于工业自动化、机器人、数控机床等领域。
力矩控制是伺服电机应用中的关键技术之一,通过对伺服电机力矩的精确控制,可以实现各种复杂运动控制。
本文以某数控机床为例,介绍伺服电机力矩控制的应用案例。
二、案例背景某数控机床厂是一家专业生产数控机床的企业,其产品广泛应用于机械加工、汽车制造、航空航天等领域。
在产品研发过程中,客户对数控机床的加工精度、速度和稳定性提出了更高的要求。
为了满足客户需求,该厂决定采用伺服电机力矩控制技术来提升数控机床的性能。
三、伺服电机力矩控制方案1. 系统组成该数控机床伺服电机力矩控制系统主要由以下部分组成:(1)伺服电机:选用高性能伺服电机,具有高精度、高响应速度和宽调速范围等特点。
(2)伺服驱动器:选用高性能伺服驱动器,实现对伺服电机的精确控制。
(3)运动控制器:采用高性能运动控制器,实现对伺服电机的力矩控制。
(4)传感器:选用高精度力矩传感器,实时监测伺服电机力矩。
(5)上位机:采用工业控制计算机作为上位机,实现对整个系统的监控和调试。
2. 力矩控制策略(1)闭环控制:采用闭环控制策略,通过力矩传感器实时监测伺服电机力矩,并与设定值进行比较,根据误差值调整伺服电机输出力矩。
(2)PID控制:采用PID控制算法对伺服电机力矩进行调节,实现对力矩的精确控制。
(3)自适应控制:根据机床加工过程和负载变化,实时调整PID参数,提高系统鲁棒性。
四、应用效果1. 提高加工精度:通过伺服电机力矩控制,实现了对加工过程中切削力的精确控制,有效降低了加工误差,提高了加工精度。
2. 提高加工速度:伺服电机力矩控制使机床在加工过程中始终保持稳定的切削力,提高了加工速度。
3. 提高稳定性:伺服电机力矩控制使机床在加工过程中具有更好的稳定性,降低了机床振动和噪音。
4. 降低能耗:通过精确控制伺服电机力矩,实现了机床的节能降耗。
五、总结伺服电机力矩控制技术在数控机床中的应用,提高了机床的加工精度、速度和稳定性,降低了能耗,具有显著的经济效益和社会效益。
垂直使用的滚珠丝杠伺服电机选型计算实例
垂直使用的滚珠丝杠伺服电机选型计算实例如下:
一、伺服电机选型步骤
1. 确定电机的机械负载:机械负载主要包括工作台、工作物和丝杠的重量,以及可能的外部负载。
在本例中,工作台重量为50kgf,工作物重量最大为25kgf,丝杠重量可以根据具体型号确定。
2. 确定电机的运动参数:运动参数包括电机的最大行程、最大速度、加速度等。
在本例中,最大行程为1000mm,最大速度为50m/min,加速度可以根据具体应用确定。
3. 确定电机的控制参数:控制参数包括定位精度和重复定位精度。
在本例中,定位精度为±/最大行程,重复定位精度为±。
4. 确定电机的驱动参数:驱动参数包括电机的最大扭矩和最大电流等。
在本例中,电机的最大扭矩和最大电流可以根据具体应用确定。
二、伺服电机选型计算
1. 计算电机的轴向力:根据机械负载的重量和重力加速度,可以计算出电机的轴向力。
在本例中,等速度时轴向力F2=μ(W1+W2)xg=(50+25)=(N),
其中μ为滑动摩擦系数,W1为工作台重量,W2为工作物重量,g为重力加速度。
2. 计算电机的转矩:根据电机的轴向力和转速,可以计算出电机的转矩。
在本例中,电机的转速可以根据具体应用确定,然后根据轴向力和转速计算出电机的转矩。
3. 确定电机型号:根据电机的运动参数、控制参数和驱动参数,以及计算出的转矩和可能的外部负载,选择适合的电机型号。
以上是垂直使用的滚珠丝杠伺服电机选型计算实例,具体计算过程可能需要根据具体情况进行调整和优化。
伺服电机计算选型应用实例伺服电机计算选型应用实例伺服电机选型实例1.选择电机时的计算条件本节叙述水平运动伺服轴(见下图)的电机选择步骤。
例:工作台和工件的W:运动部件(工作台及工件)的重量(kgf)=1000 kgf机械规格μ:滑动表面的摩擦系数=0.05π:驱动系统(包括滚珠丝杠)的效率=0.9fg:镶条锁紧力(kgf)=50 kgfFc:由切削力引起的反推力(kgf)=100 kgfFcf:由切削力矩引起的滑动表面上工作台受到的力(kgf)=30kgfZ1/Z2:变速比=1/1例:进给丝杠的(滚珠Db:轴径=32 mm丝杠)的规格Lb:轴长=1000 mmP:节距=8 mm例:电机轴的运行规格Ta:加速力矩(kgf.cm)Vm:快速移动时的电机速度(mm-1)=3000 mm-1ta:加速时间(s)=0.10 sJm:电机的惯量(kgf.cm.sec2)Jl:负载惯量(kgf.cm.sec2)ks:伺服的位置回路增益(sec-1)=30 sec-11.1负载力矩和惯量的计算计算负载力矩加到电机轴上的负载力矩通常由下式算出:Tm = + TfTm:加到电机轴上的负载力矩(Nm)F:沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf)L:电机转一转机床的移动距离=P×(Z1/Z2)=8 mmTf:滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2Nm无论是否在切削,是垂直轴还是水平轴,F值取决于工作台的重量,摩擦系数。
若坐标轴是垂直轴,F值还与平衡锤有关。
对于水平工作台,F值可按下列公式计算:不切削时:F = μ(W+fg)例如:F=0.05×(1000+50)=52.5 (kgf)Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf)例如:F=100+0.05×(1000+50+30)=154(kgf)Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1,应根据数据单选择电机,其负载力矩在不切削时应大于0.9(Nm),最高转速应高于3000(min-1)。