第7章 一阶电路
- 格式:pdf
- 大小:231.51 KB
- 文档页数:15

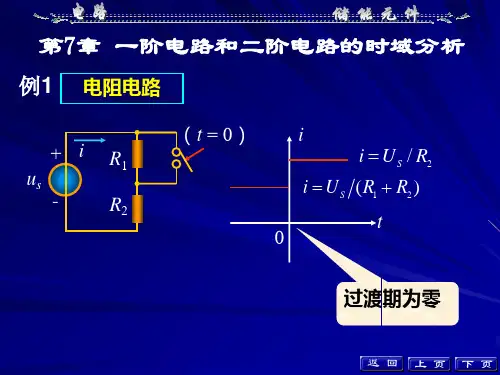


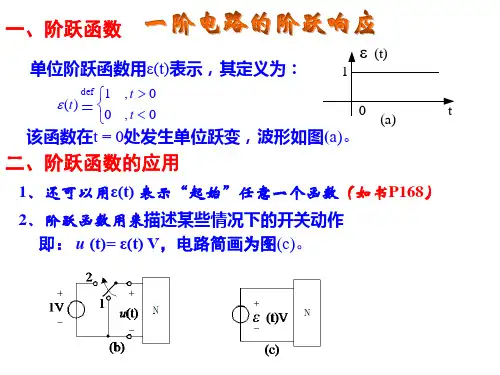
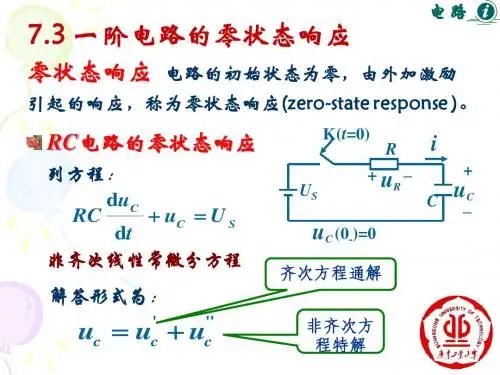


Chapter 7 一阶电路主要内容1.动态电路的方程及其初始条件;2.一阶电路(RC 电路、RL 电路)的时间常数;3.零输入响应、零状态响应、全响应、瞬态分量、稳态分量;4.三要素法;5.阶跃响应、冲激响应。
§7-1 动态电路的方程及其初始条件一、动态电路的方程1.动态电路:含有动态元件(电容或电感)的电路。
2.动态电路的方程: 电路中有储能元件(电容或电感)时,因这些元件的电压和电流的约束关系是通过导数(或积分)表达的。
根据KCL 、KVL 和支路方程式(VAR )所建立的电路方程是以电流、电压为变量的微分方程或微分-积分方程。
一阶动态电路:仅含一个动态元件的电路(RC 电路、RL 电路)。
3.动态电路的特征:当电路的结构或元件的参数发生改变时(如电源或无源元件的断开或接入,信号的突然注入等),可能使电路改变原来的工作状态,而转变到另一个工作状态。
换路:电路或参数的改变引起的电路变化。
0=t :换路时刻,换路经历的时间为 0_ 到 +0;-=0t :换路前的最终时刻; +=0t :换路后的最初时刻;4.经典法(时域分析法):根据KCL ,KVL 和VAR 建立描述电路的以时间为自变量的线性常微分方程,然后求解常微分方程,从而得到所求变量(电流或电压)的方法。
用经典法求解常微分方程时,必须根据电路的初始条件确定解答中的积分常数。
电路独立初始条件:)0(+C u 和 L i )0(+。
二、电路的初始条件1.电容的电荷和电压⎪⎪⎩⎪⎪⎨⎧+=+=⎰⎰ξξξξd tt i C t u t u d tti t q t q C C C C C C 0000)(1)()()()()(取 +-==0 ,00t t , 则⎪⎩⎪⎨⎧+=+=⎰⎰+-+--+-+ξξξξd i c u u d i q q C C C C C C 0000)(1)0()0()()0()0(若有限)( M i C ≤, 则 0)(00=⎰+-ξξd i C ,且⎩⎨⎧==-+-+)0()0()0()0(C C C C u u q q 电容上电荷和电压不发生跃变!① 若 -=0t 时,0)0(q q C =-, 0)0(U u C =-, 则有 0)0(q q C =+,)0(U u C =+, 故换路瞬间,电容相当于电压值为 0U 的电压源;② 若 -=0t 时,0)0( ,0)0(==--C C u q , 则应有)0( ,0)0(==++C C u q , 则换路瞬间,电容相当于短路。


第七章一阶电路分析一阶电路是指只包含一个电感或一个电容的电路,它们可以用来描述电路的基本性质和动态响应。
通过对一阶电路的分析,我们可以了解电路的稳态和暂态响应,从而更好地设计和优化电路。
一阶电路可以分为RL电路(含有电感)和RC电路(含有电容)两种。
它们的分析方法略有不同,下面将分别介绍这两种电路的分析方法。
一、RL电路的分析___RL__假设电压源为e(t),电阻为R,电感为L,电流为i(t)。
根据基尔霍夫电压定律,可以得到以下方程:e(t) = Ri(t) + Ldi(t)/dt将上述方程进行拉普拉斯变换,得到:E(s)=RI(s)+sLI(s)-Li(0)其中E(s)和I(s)为拉普拉斯变换后的电压和电流,Li(0)为电流在t=0时刻的初值。
将上述方程化简,得到:I(s)=E(s)/(sL+R)将上述方程进行反变换,得到电流i(t)的表达式:i(t) = (1/L) * ∫[0,t] E(t') * exp[-(t-t')/τ] dt'其中τ=L/R为电路的时间常数,代表电流上升至最终稳定值的时间。
二、RC电路的分析____EC___假设电压源为E(t),电阻为R,电容为C,电流为I(t)。
根据基尔霍夫电压定律,可以得到以下方程:E(t) = Ri(t) + 1/C ∫[0,t] i(t')dt'将上述方程进行拉普拉斯变换,得到:E(s)=RI(s)+I(s)/sC其中E(s)和I(s)为拉普拉斯变换后的电压和电流。
将上述方程化简,得到:I(s)=E(s)/(sRC+1)将上述方程进行反变换,得到电流i(t)的表达式:i(t) = (1/RC) * ∫[0,t] E(t') * exp[-(t-t')/τ] dt'其中τ=RC为电路的时间常数,代表电流上升至最终稳定值的时间。
通过对RL电路和RC电路的分析,我们可以得到它们的电流响应和电压响应。

教 案课程: 电路分析基础内容: 第七章 一阶电路课时:12学时教师:刘 岚课题一阶电路科目电路分析基础课时12学时教师刘岚授课班级时间教学目的与要求知识目标:1、动态电路方程的建立及初始条件的确定。
2、一阶电路的零输入响应、零状态响应和全响应求解。
3、稳态分量、暂态分量求解。
4、一阶电路的阶跃响应和冲激响应。
能力目标:培养学生的想象力及利用所学知识分析、总结问题的能力。
情感目标:激发学生对电路分析基础的学习热情。
教学重点用微分方程的经典解法分析一阶电路和二阶电路;求解零输入响应、零状态响应和全响应,及电路的特解、通解,稳态响应,暂态响应,阶跃响应和冲激响应。
教学难点一阶电路相应微分方程的列写是本章学习中的难点。
教学方法讲述法、演示法、发现法、讨论法教学环境多媒体教室教学准备多媒体课件教学过程1、复习提问 2、引入新课 3、讲解新课 4、归纳总结6、布置作业通过演示、多媒体教学软件与传统教学相结合,使教学过程更生动、直观,学生更易接受及课后记载产生学习兴趣。
探究式教学的应用可让学生结合所学知识,通过自主地观察、分析得出结论,培养了独立思维能力。
第7章 一阶电路教 案(一)教学内容:深刻理解下列概念:动态电路,过渡过程,状态、初始状态,换路定则,固有频率,时间常数,零输入响应,零状态响应,全响应,阶跃响应,冲激响应,非时变特性,自由分量,强制分量,暂态分量,稳态分量,三要素法。
熟练掌握一阶电路微分方程的建立,初始条件的求取与微分方程的求解。
熟练掌握利用戴维南定理结合三要素法直接求出一阶电路的全响应。
掌握非时变特性和线性函数的概念在一阶电路中的应用。
掌握阶跃响应、冲激响应的求法。
(二)重点:动态电路及其分析中的各种基本概念。
换路定则及用换路定则求初始条件。
微分方程的建立与求解。
戴维南定理结合三要素法在一阶电路分析中的应用。
难点:利用线性特性与非时变特性求一阶电路的零状态响应。
冲激响应的概念及各种求解方法。
求解微分方程时决定积分常数所需初始条件的确定。
(三)学时教学环节讲课习题课小计课程内容 学时动态电路及方程、电路初始条件22一阶电路的零输入响应112一阶电路的零状态响应112一阶电路的全响应112一阶电路的阶跃响应112一阶电路的冲激响应112(四)概述本章的主要内容是讨论用微分方程描述的动态电路,RC RL电路,介绍分析一阶电路过渡过程的经典法及一阶电教学环节教学过程复习引入新课讲述新课简单回顾上次课的知识点。
通过第六章的学习,我们注意到电容和电感的一个重要特性是,它们都具有存储能量的能力。
可以确定一个电感或电容释放或得到能量时产生的电流和电压。
在这一章我们将学习由电源、电阻、电容(或电感)组成的电路。
多媒体课件展示:第七章 一阶电路一、设置悬念、激发探究在日常生活中需要闪光灯的场合非常多。
照相机在光线比较暗的条件下照相,需要用闪光灯照亮场景一定时间,将影像记录在胶卷或存储设备上。
一般来说,照相机闪光灯电路需要重新充电后才能再照下一张照片。
还有些场合使用按一定时间间隔自动闪光的闪光灯作为危险警告,例如,高的天线塔、建筑工地和安全地带等。
那么类似这样的电路应该如何分析呢?我们在这一章就将详细学习。
二、动态电路及初始条件多媒体课件展示:7.1 动态电路的方程及其初始条件1.动态电路:电容元件和电感元件的电压和电流的约束关系是通过导数(或积分)表达的,所以称为动态元件。
当电路中含有动态元件时被称为动态电路。
特点:当动态电路状态发生改变时(换路)需要经历一个变化过程才能达到新的稳定状态。
这个变化过程称为电路的过渡过程。
动态电路的过渡过程:多媒体课件展示。
换路:电路结构、状态发生变化(①支路接入或断开;②电路参数变化)。
过渡过程产生的原因:电路内部含有储能元件 L 、C,电路在换路时能量发生变化,而能量的储存和释放都需要一定的时间来完成。
2. 动态电路的方程动态电路的方程:多媒体课件展示。
结论:(1)描述动态电路的电路方程为微分方程;(2)动态电路方程的阶数等于电路中动态元件的个数。
一阶电路:一阶电路中只有一个动态元件,描述电路的方程是一阶线性微分方程。
动态电路的分析方法:(1)根据KVl、KCL和VCR建立微分方程;(2)求解微分方程。
3. 电路的初始条件(1) t = 0+与t = 0-的概念认为换路在 t=0时刻进行则:0- 换路前一瞬间0+ 换路后一瞬间初始条件为 t = 0+时电路中所求变量(电压或电流)及其各阶导数的值,也称为初始值。
在动态电路的分析中,初始条件是得到确定解答的必需条件。
(2) 电容的初始条件换路瞬间,若电容电流保持为有限值, 则电容电压(电荷)换路前后保持不变。
(3) 电感的初始条件换路瞬间,若电感电压保持为有限值, 则电感电流(磁链)换路前后保持不变。
(4)换路定律换路瞬间,若电容电流保持为有限值, 则电容电压(电荷)换路前后保持不变。
换路瞬间,若电感电压保持为有限值, 则电感电流(磁链)换路前后保持不变。
注意:(1)电容电流和电感电压为有限值是换路定律成立的条件。
(2)换路定律反映了能量不能跃变。
5.电路初始值的确定求初始值的步骤:(1)由换路前电路(一般为稳定状态)求u C(0-)和i L(0-);(2)由换路定律得 u C(0+) 和 i L(0+)。
(3)画0+等效电路。
a.换路后的电路b. 电容用电压源替代。
电感用电流源替代。
(取0+时刻值,方向与原假定的电容电压、电感电流方向相同)。
(4)由0+电路求所需各变量的0+值。
电路初始值的确定例题:多媒体课件展示。
三、一阶电路的响应多媒体课件展示:7.2 一阶电路的零输入响应零输入响应:换路后外加激励为零,仅由动态元件初始储能所产生的响应,称为动态电路的零输入响应。
1.RC电路的零输入响应多媒体课件展示。
一阶RC电路的零输入响应有以下特点:(1)换路瞬间电容电压保持不变,电流发生突变形成放电过程。
换路后,所有的响应都是按相同的指数规律衰减。
(2)衰减的指数规律仅由电路的结构和参数决定,与变量的选择无关。
(3)衰减的速度取决于1/RC (衰减系数)。
令 =RC, 具有时间的量纲,称为一阶电路的时间常数。
令 ,p具有频率的量纲,称为固有频率。
时间常数 的大小反映了电路过渡过程时间的长短:大 → 过渡过程时间长(越大,衰减越慢,放电时间越长)小 → 过渡过程时间短(越小,衰减越快,放电时间越短)(4)响应与其初始值成线性关系。
初始值增大几倍,响应增大几倍。
(5)一阶RC电路的零输入响应是靠电容中储存的电场能的释放维持,释放的能量同时被电阻消耗, 暂态过程最后以能量的耗尽而告终。
此为一阶RC电路的零输入响应的实质。
一阶RC电路的零输入响应的求解步骤:(1)求解电路换路前的状态。
归纳总结布置作业(2)求解电路换路后的初始值。
(3)求时间常数 =RC,R为换路后从电容两个端纽看进去的等效电阻。
(4)带入零输入响应表达式。
例题:多媒体课件展示。
2. RL电路的零输入响应多媒体课件展示。
一阶RL电路的零输入响应有以下特点:(1)换路瞬间电感电流保持不变,电压发生突释放磁场能。
换路后,所有的响应都是按相同的指数规律衰减。
(2)衰减的指数规律仅由电路的结构和参数决定,与变量的选择无关。
(3)衰减的速度取决于R/L(衰减系数)。
令 =L/R, 具有时间的量纲,称为一阶电路的时间常数。
令 ,p具有频率的量纲,称为固有频率。
时间常数 的大小反映了电路过渡过程时间的长短:大 → 过渡过程时间长(越大,衰减越慢,放电时间越长)小 → 过渡过程时间短(越小,衰减越快,放电时间越短)(4)响应与其初始值成线性关系。
初始值增大几倍,响应增大几倍。
(5)一阶RL电路的零输入响应是靠电感中储存的磁场能的释放维持,释放的能量同时被电阻消耗, 暂态过程最后以能量的耗尽而告终。
此为一阶RL电路的零输入响应的实质。
一阶RL电路的零输入响应的求解步骤:(1)求解电路换路前的状态。
(2)求解电路换路后的初始值。
(3)求时间常数 =L/R,R为换路后从电感两个端纽看进去的等效电阻。
(4)带入零输入响应表达式。
例题:多媒体课件展示。
小结:(1)一阶电路的零输入响应是由储能元件的初值引起的响应, 都是由初始值衰减为零的指数衰减函数。
响应模式为:(2)衰减快慢取决于时间常数RC电路 = RC , RL电路 = L/RR为与动态元件相连的一端口电路的等效电阻。
(3)同一电路中所有响应具有相同的时间常数。
(4)一阶电路的零输入响应和初始值成正比,称为零输入线性。
多媒体课件展示:7.3 一阶电路的零状态响应零状态响应:动态元件初始能量为零,由t >0电路中外加输入激励作用所产生的响应。
1. RC电路的零状态响应多媒体课件展示。
一阶RC电路的零状态响应有以下特点:(1)电容上电压(状态)从初始值开始逐渐增加,最后达到新的稳定值。
它有两部分组成:a. 稳态分量:方程的特解,即电路达到稳态时的稳态值。
它受外施激励源制约,也称为强制分量。
b. 暂态分量:方程的通解,其变化规律与零输入响应相同,按指数规律衰减为零,只在暂态过程中出现,故称为暂态分量。
其形式与外施激励源无关,也称为自由分量。
(2)电流在换路瞬间发生突变,其值为Us/R,即换路后的初始值,电路以此值开始给电容充电,随着极板上的电荷增多,电容电压的增大,i=(Us-u c)/R减小,最后为零,电容电压为Us。
(3)响应变化的快慢,由时间常数=RC决定;大,充电慢,小充电就快。
(4)响应与外加激励具有正比例关系。
(5)一阶RC电路的零状态响应实质是电路储存电场能的过程。
电源在充电过程中提供的能量,一部分转化成电场能储存在电容中,一部分被电路中的电阻消耗,且有Wc=W R,电源提供的能量只有一半储存在电容中,充电效率50%,与电阻电容数值无关。
例题:多媒体课件展示。
2. RL电路的零状态响应一阶RL电路的零状态响应有以下特点:(1)电感上电流(状态)从初始值开始逐渐增加,最后达到新的稳定值。
其稳态分量和暂态分量的意义与RC电路相同。
(2)电压在换路瞬间发生突变,其值为Us,即换路后的初始值,电路以此值开始在线圈中储存磁场能。
(3)响应变化的快慢,由时间常数=L/R决定;大,储能慢,小储能就快。
(4)响应与外加激励具有正比例关系。
(5)一阶RL电路的零状态响应实质是电路储存磁场能的过程。
电源在此过程中提供的能量,一部分转化成磁场能储存在电感中,一部分被电路中的电阻消耗,且有W L=W R,电源提供的能量只有一半储存在电感中,储能效率50%,与电阻电感数值无关。
外施激励源为直流时的一阶电路的零状态响应的求解步骤如下:(1)求出换路后动态元件以外的戴维宁等效电路。
(2)根据状态变量的响应模式得到:(3)将电容看作电压源、电感看作电流源回到换路后的原电路按电路的基本约束关系求解其它电压和电流。