《142微积分基本定理》导学案5.doc

1.4.2 微积分基本定理【学习要求】会应用定积分求两条或多条曲线围成的图形的面积．【学法指导】本小节主要解决一些在几何中用初等数学方法难以解决的平面图形面积问题．在这部分的学习中，应特别注意利用定积分的几何意义，借助图形直观，把平面图形进行适当的分割，从而把求平面图形面积的问题转化为求曲边梯形面积的问题.1．当x ∈[a ，b]时，若f(x)>0，由直线x ＝a ，x ＝b(a≠b)，y ＝0和曲线y ＝f(x)所围成的曲边梯形的面积S ＝__ ʃb a f(x)dx______.2．当x ∈[a ，b]时，若f(x)<0，由直线x ＝a ，x ＝b(a≠b)，y ＝0和曲线y ＝f(x)所围成的曲边梯形的面积S ＝___－ʃb a f(x)dx______.3．当x ∈[a ，b]时，若f(x)>g(x)>0时，由直线x ＝a ，x ＝b(a≠b)和曲线y ＝f(x)，y ＝g(x)围成的平面图形的面积S ＝__ ʃb a [f(x)－g(x)]dx____________.(如图)探究点一 求不分割型图形的面积问题 怎样利用定积分求不分割型图形的面积？答 求由曲线围成的面积，要根据图形，确定积分上下限，用定积分来表示面积，然后计算定积分即可． 例1 计算由曲线y 2＝x ，y ＝x 2所围图形的面积S.解 由⎩⎪⎨⎪⎧y 2＝x ，y ＝x 2得交点的横坐标为x ＝0及x ＝1. 因此，所求图形的面积为S ＝S 曲边梯形OABC －S 曲边梯形OABD＝ʃ10xdx －ʃ10x 2dx ＝23 |10－13x 3|10＝23－13＝13. 小结 求由曲线围成图形面积的一般步骤：(1)根据题意画出图形；(2)找出范围，确定积分上、下限；(3)确定被积函数；(4)将面积用定积分表示；(5)用微积分基本定理计算定积分，求出结果．跟踪训练1 求由抛物线y ＝x 2－4与直线y ＝－x ＋2所围成图形的面积．解 由⎩⎪⎨⎪⎧y ＝x 2－4y ＝－x ＋2 得⎩⎪⎨⎪⎧ x ＝－3y ＝5或⎩⎪⎨⎪⎧x ＝2y ＝0，所以直线y ＝－x ＋2与抛物线y ＝x 2－4的交点为(－3,5)和(2,0)，设所求图形面积为S ，根据图形可得S ＝ʃ2－3(－x ＋2)dx －ʃ2－3(x 2－4)dx＝(2x －12x 2)|2－3－(13x 3－4x)|2－3 ＝252－(－253)＝1256. 32x探究点二 分割型图形面积的求解问题 由两条或两条以上的曲线围成的较为复杂的图形，在不同的区间位于上方和下方的曲线不同时，这种图形的面积如何求呢？答 求出曲线的不同的交点横坐标，将积分区间细化，分别求出相应区间曲边梯形的面积再求和，注意在每个区间上被积函数均是由上减下．例2 计算由直线y ＝x －4，曲线y ＝2x 以及x 轴所围图形的面积S.解 方法一 作出直线y ＝x －4，曲线y ＝2x 的草图．解方程组⎩⎪⎨⎪⎧ y ＝2x ，y ＝x －4 得直线y ＝x －4与曲线y ＝2x 交点的坐标为(8,4)．直线y ＝x －4与x 轴的交点为(4,0)．因此，所求图形的面积为S ＝S 1＋S 2＝ʃ402xdx ＋⎰⎰--8484]d )4(d 2[x x x x＝403. 方法二 把y 看成积分变量，则S ＝ʃ40(y ＋4－12y 2)dy ＝(12y 2＋4y －16y 3)|40＝403. 小结 两条或两条以上的曲线围成的图形，一定要确定图形范围，通过解方程组求出交点的坐标，定出积分上、下限，若积分变量选x 运算较繁锁，则积分变量可选y ，同时要更换积分上、下限．跟踪训练2 求由曲线y ＝x ，y ＝2－x ，y ＝－13x 所围成图形的面积．解 画出图形，如图所示．解方程组⎩⎪⎨⎪⎧ y ＝x ，x ＋y ＝2，⎩⎪⎨⎪⎧ y ＝x ，y ＝－13x ， 及⎩⎪⎨⎪⎧x ＋y ＝2，y ＝－13x ，得交点分别为(1,1)，(0,0)，(3，－1)，所以S ＝ʃ10[x －(－13x)]dx ＋ʃ31[(2－x)－(－13x)]dx ＝ʃ10(x ＋13x)dx ＋ʃ31(2－x ＋13x)dx＝223 |40＋223 |84－12(x －4)2|8432x 32x ＝(23 ＋16x 2)|10＋(2x －12x 2＋16x 2)|3132x＝23＋16＋(2x －13x 2)|31 ＝56＋6－13×9－2＋13＝136. 探究点三 定积分的综合应用例3 在曲线y ＝x 2(x≥0)上某一点A 处作一切线使之与曲线以及x 轴所围成的面积为112，试求： 切点A 的坐标以及在切点A 的切线方程．解 如图，设切点A(x 0，y 0)，由y′＝2x ，过点A 的切线方程为y －y 0＝2x 0(x －x 0)，即y ＝2x 0x －x 20，令y ＝0，得x ＝x 02，即C(x 02，0)， 设由曲线和过点A 的切线与x 轴围成图形的面积为S ，则S ＝S 曲边△AOB －S △ABC ，S △ABC ＝12|BC|·|AB|＝12(x 0－x 02)·x 20＝14x 30. ∴S ＝13x 30－14x 30＝112x 30＝112.所以x 0＝1， 从而切点为A(1,1)，切线方程为2x －y －1＝0.小结 本题综合考查了导数的意义以及定积分等知识，运用待定系数法，先设出切点的坐标，利用导数的几何意义，建立了切线方程，然后利用定积分以及平面几何的性质求出所围成的平面图形的面积，根据条件建立方程求解，从而使问题得以解决．跟踪训练3 如图所示，直线y ＝kx 分抛物线y ＝x －x 2与x 轴所围图形为面积相等的两部分，求k 的值． 解 抛物线y ＝x －x 2与x 轴两交点的横坐标为x 1＝0，x 2＝1，所以，抛物线与x 轴所围图形的面积S ＝ʃ10(x －x 2)dx ＝⎝⎛⎭⎫x 22－13x 3|10＝16. 又⎩⎪⎨⎪⎧y ＝x －x 2，y ＝kx ， 由此可得，抛物线y ＝x －x 2与y ＝kx 两交点的横坐标为x 3＝0，x 4＝1－k ，所以，S 2＝ʃ1－k 0(x －x 2－kx)dx ＝⎝⎛⎭⎫1－k 2x 2－13x 3|1－k 0＝16(1－k)3. 又知S ＝16，所以(1－k)3＝12， 于是k ＝1－ 312＝1－342. 4．由曲线y ＝x 2＋4与直线y ＝5x ，x ＝0，x ＝4所围成平面图形的面积是___193___． 解析 由图形可得S ＝ʃ10(x 2＋4－5x)dx ＋ʃ41(5x －x 2－4)dx ＝(13x 3＋4x －52x 2)|10＋(52x 2－13x 3－4x)|41 ∵S 曲边△AOB ＝ʃ x 2d x ＝13x 3| ＝13x 30，00x00x＝13＋4－52＋52×42－13×43－4×4－52＋13＋4＝193. 对于简单图形的面积求解，我们可直接运用定积分的几何意义，此时(1)确定积分上、下限，一般为两交点的横坐标．(2)确定被积函数，一般是上曲线与下曲线对应函数的差．这样所求的面积问题就转化为运用微积分基本定理计算定积分了．注意区别定积分与利用定积分计算曲线所围图形的面积：定积分可正、可负或为零；而平面图形的面积总是非负的.。

2019-2020学年高中数学《16 微积分基本定理》导学案 新人教A 版
选修2-2
一、学习目标：
知识与技能：能利用微积分基本定理及定积分的几何意义正确、灵活求定积分的值。

过程与方法：通过例题，体验定理求定积分的值的优越性，形成求定积分的值的这类问题的思想方法
情感态度与价值观：学生能做到学以致用，树立学生学习数学的自信心。

二、重点难点：
重点：微积分基本定理的理解及应用
难点：求被积函数的原函数
三、知法链接：
1、微积分基本定理
2、定积分的几何意义
3、定积分运算性质
4、基本初等函数的求导公式及复合函数的求导法则
四、学习过程：
总结：
（2）
⎰π0cos xdx ⎰0sin πxdx
dx x x ⎰-2
1)1( dx x
e x ⎰-21)2(
总结：
（3）⎰102dx e x ⎰46
2cos ππxdx
总结：
（4）dx x x 232)1(⎰+ dx x
x x ⎰--2
1232
总结：
题型二
求下列定积分的值
dx x ⎰-1021 dx x ⎰-1024
课堂总结：
求定积分的方法
作业:
一生的生活是否幸福、平安、吉祥、要看他的处世为人是否道德无亏，能否做社会的表率。

课题：1.6微积分基本定理一、学习目标1.通过实例直观了解微积分积分定理的含义.2.熟练地用微积分积分定理计算微积分.二、教学重难点教学重点：理解微积分基本定理的含义，并能用定理计算简单的定积分．教学难点：理解微积分基本定理的含义．三、自学指导与检测自学指导自学检测及课堂展示阅读课本54-51P完成右框内容1.复习定积分的性质①bakf(x)dx=⎰ .②b12a[f(x)f(x)]dx=±⎰ .③baf(x)dx=⎰ .2.微积分基本定理(1)一般地，如果)(xf是区间[]b a,上的连续函数并且)()(xfxF=',那么=⎰b a dxxf)(___________ .这个结论叫做微积分基本定理，也叫做. (2)符合表示：=⎰b a dxxf)(= .【即式训练1】用微积分基本定理求简单函数的定积分．（1）12x dx⎰；（2）()dxxx⎰-122；（3）⎰102dxe x（4）⎰--22)4)(24(dxxx【变式训练1】计算下列定积分:⎰π0sin xdx,⎰ππ2sin xdx,⎰π20sin xdx.由计算结果你能发现什么结论?试利用曲边梯形的面积表示所发现的结论.3：用微积分基本定理求分段函数的定积分A 层1．下列积分正确的是( )2.dx x ⎰--1121等于( )A.4πB.2π C.π D.π2B 层3.dx x ⎰11-等于() A.⎰11-xdx B. dx ⎰11- C. ⎰-01-)(dx x ＋⎰10xdx D. ⎰01-xdx ＋⎰-10)(dx xC 层5.已知⎰--=-aa dx x 8)12(,求a 的值.【即时训练2】.求函数3(01)()(14)x x f x x x ⎧≤≤⎪=⎨<≤⎪⎩在区间[0,4]上的积分.。

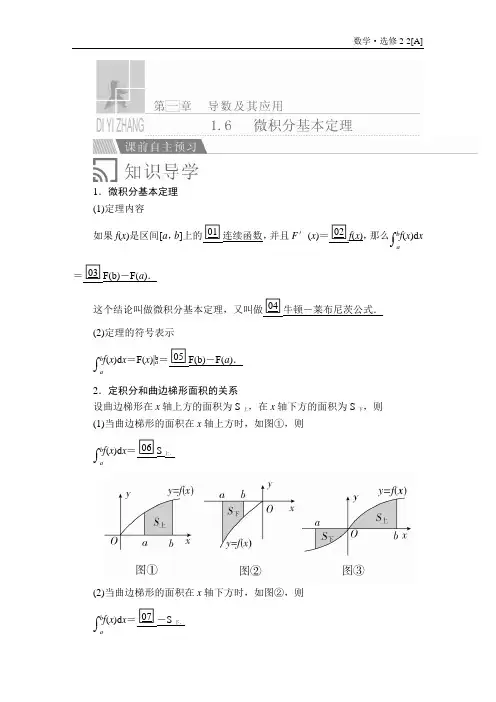
1．微积分基本定理(1)定理内容如果f(x)是区间[a，b]上的□01连续函数，并且F′(x)＝□02f(x)，那么⎠⎛ab f(x)d x ＝□03F(b)－F(a)．这个结论叫做微积分基本定理，又叫做□04牛顿－莱布尼茨公式．(2)定理的符号表示⎠⎛ab f(x)d x＝F(x)|b a＝□05F(b)－F(a)．2．定积分和曲边梯形面积的关系设曲边梯形在x轴上方的面积为S上，在x轴下方的面积为S下，则(1)当曲边梯形的面积在x轴上方时，如图①，则⎠⎛ab f(x)d x＝□06S上．(2)当曲边梯形的面积在x轴下方时，如图②，则⎠⎛ab f(x)d x＝□07－S下．(3)当曲边梯形的面积在x轴上方、x轴下方均存在时，如图③，则⎠⎛ab f(x)d x＝□08S上－S下．若S上＝S下，则⎠⎛ab f(x)d x＝□090.1．判一判(正确的打“√”，错误的打“×”)(1)微积分基本定理中，被积函数f(x)是原函数F(x)的导数．()(2)应用微积分基本定理求定积分的值时，为了计算方便通常取原函数的常数项为0.()(3)应用微积分基本定理求定积分的值时，被积函数在积分区间上必须是连续函数．()答案(1)√(2)√(3)√答案(1)0(2)2(3)2拓展提升求简单的定积分要注意的两点(1)掌握基本函数的导数以及导数的运算法则，正确求解被积函数的原函数，当原函数不易求时，可将被积函数适当变形后再求解；(2)精确定位积分区间，分清积分下限与积分上限．[条件探究] 将本例中的2改为a ，求⎠⎛－43|x ＋a |d x .拓展提升求分段函数的定积分时，可利用积分性质将其表示为几段积分和的形式：(1)对于带绝对值的解析式，先根据绝对值的意义找到分界点，去掉绝对值号，化为分段函数；(2)含有字母参数的绝对值问题要注意分类讨论．【跟踪训练2】 求定积分⎠⎛13⎝⎛⎭⎪⎫|x －2|＋1x 2d x .拓展提升微积分基本定理，实际上给出了导数和定积分之间的内在联系，在求解含有参数的定积分问题时，往往要与其他知识联系起来，综合解决．一般地，首先要弄清楚积分变量和被积函数．当被积函数中含有参数时，必须分清常数和变量，再进行计算；其次要注意积分下限不大于积分上限．答案(1)1(2)3 31.求定积分的一些常用技巧(1)对被积函数，要先化简，再求积分.(2)若被积函数是分段函数，依据定积分“对区间的可加性”，分段积分再求和.(3)对于含有绝对值符号的被积函数，要去掉绝对值符号后才能积分.2.由于定积分的值可取正值，也可取负值，还可以取0，而面积都是正值，因此不要把面积理解为被积函数对应图形在某几个区间上的定积分之和．在x轴下方的图形面积要取定积分的相反数.答案 A解析设f(x)＝ax＋b，代入可得a＝4，b＝3.2．定积分⎠⎛1(2x＋e x)d x的值为()A．e＋2 B．e＋1 C．e D．e－1答案C解析⎠⎛1(2x＋e x)d x＝(x2＋e x)|10＝(1＋e)－(0＋e0)＝e.3．已知f(x)＝3x2＋2x＋1，若⎠⎜⎛-11f(x)d x＝2f(a)成立，则a＝________.答案－1或13解析由已知F(x)＝x3＋x2＋x，F(1)＝3，F(－1)＝－1，所以⎠⎜⎛-11f(x)d x＝F(1)－F(－1)＝4，所以2f(a)＝4，所以f(a)＝2，即3a2＋2a＋1＝2.解得a＝－1或13.4．已知f(x)为一次函数，且f(x)＝x＋2⎠⎛1f(t)d t，则f(x)＝________.答案x－1解析设f(x)＝kx＋m(k≠0)，则⎠⎛1f(t)d t＝⎝⎛⎭⎪⎫12kt2＋mt10＝12k＋m，∴kx ＋m ＝x ＋k ＋2m ，∴k ＝1且m ＝k ＋2m ，∴m ＝－1.即f (x )＝x －1.5．已知f (x )＝ax 2＋b x ＋c(a ≠0)，且f (－1)＝2，f ′(0)＝0，⎠⎛01f (x )d x ＝－2，求a ，b ，c 的值．解 由f (－1)＝2得a －b ＋c ＝2，① 又f ′(x )＝2ax ＋b ，所以f ′(0)＝b ＝0，② 而⎠⎛01f (x )d x ＝⎠⎛01(ax 2＋b x ＋c)d x ＝⎝ ⎛⎭⎪⎫13ax 3＋12b x 2＋c x |10 ＝13a ＋12b ＋c ，所以13a ＋12b ＋c ＝－2，③由①②③式得a ＝6，b ＝0，c ＝－4.A 级：基础巩固练一、选择题1．若函数f (x )＝x m ＋nx 的导函数是f ′(x )＝2x ＋1，则⎠⎛12f (－x )d x ＝( )A.56B.12C.23D.16 答案 A解析 因为f (x )＝x m ＋nx 的导函数是f ′(x )＝2x ＋1，所以f (x )＝x 2＋x ，所以⎠⎛12f (－x )d x ＝⎠⎛12(x 2－x )d x ＝⎝ ⎛⎭⎪⎫13x 3－12x 2|21＝56.2．若⎠⎛1a ⎝ ⎛⎭⎪⎫2x ＋1x d x ＝3＋ln 2，则a 的值是( )A ．6B ．4C ．3D ．2 答案 D解析 ⎠⎛1a ⎝⎛⎭⎪⎫2x＋1x d x ＝(x 2＋ln x )a 1＝(a 2＋ln a )－(1＋ln 1)＝(a 2－1)＋ln a ＝3＋ln 2，所以⎩⎪⎨⎪⎧a 2－1＝3，a >1，a ＝2，所以a ＝2.3．设f (x )＝⎩⎨⎧x 2(0≤x <1)，2－x (1≤x ≤2)，则⎠⎛02f (x )d x 等于( )A.34B.45C.56 D ．不存在 答案 C解析 ⎠⎛02f (x )d x ＝⎠⎛01x 2d x ＋⎠⎛12(2－x )d x ，取F 1(x )＝13x 3，F 2(x )＝2x －12x 2，则F ′1(x )＝x 2，F ′2(x )＝2－x ，所以⎠⎛02f (x )d x ＝F 1(1)－F 1(0)＋F 2(2)－F 2(1)＝13－0＋2×2－12×22－⎝ ⎛⎭⎪⎫2×1－12×12＝56.答案 D答案 A答案 B二、填空题7．若f (x )在R 上可导，f (x )＝x 2＋2f ′(2)x ＋3，则⎠⎛03f (x )d x ＝________.答案 －18解析 ∵f (x )＝x 2＋2f ′(2)x ＋3.∴f ′(x )＝2x ＋2f ′(2)，∴f ′(2)＝4＋2f ′(2)， ∴f ′(2)＝－4.∴f (x )＝x 2－8x ＋3，∴⎠⎛03f (x )d x ＝⎠⎛03(x 2－8x ＋3)d x ＝⎝ ⎛⎭⎪⎫13x 3－4x 2＋3x |30＝－18. 8．计算定积分⎠⎜⎛-11(x 2＋sin x )d x ＝________.答案 23解析 因为⎝ ⎛⎭⎪⎫13x 3－cosx ′＝x 2＋sin x ，所以⎠⎜⎛-11 (x 2＋sin x )d x ＝⎝ ⎛⎭⎪⎫13x 3－cosx |1－1＝23.9．定积分⎠⎛01x1＋x 2d x 的值为______． 答案 12ln 2解析 因为⎣⎢⎡⎦⎥⎤12 ln (1＋x 2)′＝x 1＋x 2，所以⎠⎛01x 1＋x 2d x ＝12 ln (1＋x 2)|10＝12 ln 2.B 级：能力提升练11．已知f (a )＝⎠⎛01(2ax 2－a 2x )d x ，求f (a )的最大值．解 ∵⎝ ⎛⎭⎪⎫23ax 3－12a 2x 2′＝2ax 2－a 2x ，∴⎠⎛01(2ax 2－a 2x )d x ＝⎝ ⎛⎭⎪⎫23ax 3－12a 2x 2|10 ＝23a －12a 2， 即f (a )＝23a －12a 2 ＝－12⎝ ⎛⎭⎪⎫a 2－43a ＋49＋29 ＝－12⎝ ⎛⎭⎪⎫a －232＋29，∴当a ＝23时，f (a )有最大值29.12．已知f (x )＝⎩⎨⎧2x ＋1，x ∈[－2，2)，1＋x 2，x ∈(2，4]，求使⎠⎛k 3f (x )d x ＝403恒成立的k 的值． 解 由题意得k<3. (1)当k ∈(2,3)时， ⎠⎛k3f (x )d x ＝⎠⎛k3(1＋x 2)d x ＝⎝⎛⎭⎪⎫x ＋13x 3|3k＝3＋13×33－⎝ ⎛⎭⎪⎫k ＋13k 3＝403，整理得k 3＋3k ＋4＝0，即k 3＋k 2－k 2＋3k ＋4＝0， 所以(k ＋1)(k 2－k ＋4)＝0，所以k ＝－1. 而k ∈(2,3)，所以k ＝－1舍去． (2)当k ∈[－2,2]时，⎠⎛k 3f (x )d x ＝⎠⎛k 2(2x ＋1)d x ＋⎠⎛23(1＋x 2)d x ＝(x 2＋x )2k ＋⎝ ⎛⎭⎪⎫x ＋13x 332 ＝(22＋2)－(k 2＋k )＋⎝ ⎛⎭⎪⎫3＋13×33－⎝ ⎛⎭⎪⎫2＋13×23＝403－(k 2＋k )＝403， 所以k 2＋k ＝0， 解得k ＝0或k ＝－1. 综上所述，k ＝0或k ＝－1.。

sx-14-(2-2)-0261.6《微积分基本定理》导学案编写：刘威 审核：陈纯洪 编写时间:2014.5.13班级＿＿＿＿＿组名＿＿＿＿＿＿＿姓名＿＿＿＿＿＿＿等级＿＿＿＿＿＿＿【学习目标】1. 通过实例，直观了解微积分基本定理的含义，会用牛顿-莱布尼兹公式求简单的定积分；2. 通过探究变速直线运动物体的速度与位移的关系，使学生直观了解微积分基本定理的含义，并能正确运用基本定理计算简单的定积分。

【重点与难点】：重点：微积分基本定理（牛顿-莱布尼兹公式及其运用 难点：微积分基本定理的含义 【知识链接】知识点一：微积分基本定理自学教材 51—53页.探究一下导数和定积分的联系).知识点二：利用微积分基本定理求定积分阅读教材53-54，完成下列问题()()1322220111::1;22;(3)(2cos sin 1)dx x dx x x dx x x π--⎛⎫-+- ⎪⎝⎭⎰⎰⎰例计算下列定积分202:,()f x dx ≤≤⎧⎨≤⎩⎰2x 0x 1例设f(x)=求5 1<x 2感悟提升：,微积分基本定理揭示了导数和定积分之间的内在联系同时它也提供了计算定积分的一种()()()()()'.,.b af x dx F x f x F x F x =⎰计算定积分的关键是找到满足的函数通常我们可以运用基本初函数的求导公式和导数的四则运算法则从反方向求出【小结】1.微积分基本定理（牛顿—莱布尼茨公式）：2.变速直线运动中位移函数与速度函数的联系：3.利用微积分基本定理求定积分的方法步骤：【当堂检测】1.计算下列各定积分：（1）220(42)(4)x x --⎰ （2）1dx ⎰（3）212()x e dx x-⎰2. （1）计算定积分30sin xdxπ⎰的值，并从几何上解释这个值表示什么（2）计算定积分2sin x dxπ⎰.【课后反思】本节课我还有哪些疑惑？。

《1.4.2 微积分基本定理（2）》教学案3 【学情分析】：在上一节教学中，学生已经学习了微积分基本定理，并且初步学会使用微积分基本定理进行求定积分的计算．本节需要在上一节的基础上，进一步理解定积分的几何意义，以及利用几何意义求几何图形的面积．学生在学习了几种初等函数，必然会设法计算它们的一些定积分．另外学生在之前还学习一些具有特殊函数性质(奇偶性)的函数，这些函数也是可以作为研究的对象．【教学目标】：(1)知识与技能：进一步熟悉运用基本定理求定积分；增强函数知识的横向联系；(2)过程与方法：理解定积分的值与曲边梯形面积之间的关系；(3)情感态度与价值观：培养学生的探究精神与创新思想。

【教学重点】：(1)运用基本定理求定积分(2)定积分的值与曲边梯形面积之间的关系【教学难点】：(1)求函数()f x的一个原函数()F x(2)理解定积分的值与曲边梯形面积之间的关系【教学突破点】：合理利用复合函数的求导法则来求原函数()F x【教学过程设计】：1.22(sin cos )d x x xππ-+⎰的值是( )(A)0 (B)4π(C)2 (D)4答案：C 解释：()2222(sin cos )d cos sin 2x x x x x ππππ--+=-+=⎰2. 曲线3cos (0)2y x x π=≤≤与坐标轴所围成的面积是( )(A)2 (B)3 (C)52(D)4答案：B 解释：332222cos d cos d (cos )d S x x x x x xππππ==+-⎰⎰⎰3202sin sin 123x x πππ=-=+=3.sin (02)y x x π=≤≤与x 轴所围成图形的面积为答案：4 解释：220sin d sin d sin d x x x x x xππππ=+⎰⎰⎰20cos (cos )4x x πππ=--=4. 设201()512x x f x x ≤≤⎧=⎨<≤⎩，求20()f x dx ⎰。

微积分基本定理教案教案标题：微积分基本定理教案教学目标：1. 理解微积分基本定理的概念和意义；2. 掌握微积分基本定理的两个部分：第一部分——积分与原函数的关系，第二部分——定积分的计算；3. 能够运用微积分基本定理解决与函数积分和定积分相关的问题。

教学准备：1. 教材：微积分教材；2. 教具：黑板、粉笔、投影仪；3. 学生辅助教学资料：练习题、习题答案。

教学过程：一、导入（5分钟）1. 利用导数的概念引出积分的概念，复习导数的定义和求导法则。

2. 提问学生：如果已知一个函数的导数，能否还原出原函数？为什么？二、讲解微积分基本定理的第一部分（10分钟）1. 定义积分和原函数的关系：如果函数F(x)在[a, b]上连续，且F'(x) = f(x)，则∫[a, b] f(x) dx = F(b) - F(a)。

2. 通过例题演示如何利用微积分基本定理第一部分求函数的不定积分。

三、练习与讨论（15分钟）1. 分发练习题，让学生独立完成。

2. 学生互相交流，讨论解题思路和答案。

3. 对部分练习题进行讲解和解答，引导学生理解微积分基本定理的应用。

四、讲解微积分基本定理的第二部分（10分钟）1. 定义定积分的概念：如果函数f(x)在[a, b]上连续，则∫[a, b] f(x) dx表示函数f(x)在[a, b]上的面积或曲线长度。

2. 引出微积分基本定理的第二部分：如果函数f(x)在[a, b]上连续，且F(x)是f(x)的一个原函数，则∫[a, b] f(x) dx = F(b) - F(a)。

3. 通过例题演示如何利用微积分基本定理第二部分计算定积分。

五、练习与讨论（15分钟）1. 分发练习题，让学生独立完成。

2. 学生互相交流，讨论解题思路和答案。

3. 对部分练习题进行讲解和解答，巩固学生对微积分基本定理的掌握。

六、拓展应用（10分钟）1. 提供一些实际问题，引导学生运用微积分基本定理解决与函数积分和定积分相关的问题。

教师学科教案[ 20 – 20 学年度第__学期]
任教学科：_____________
任教年级：_____________
任教老师：_____________
xx市实验学校
《1.6微积分基本定理（2）》导学案
【学法指导】
认真练习，清晰展示，积极质疑●为必背知识
【教学目标】
会用牛顿-莱布尼兹公式求简单的定积分.
【教学重点】
正确运用基本定理计算简单的定积分.
【教学难点】
熟练应用微积分基本定理的含义 .
一.知识回顾:
●定积分性质:常数与积分的关系:○1=⎰b
a dx x kf )( .
和差的积分( 推广到有限个也成立):○2
=±⎰b a dx x f x f )]()([21 . 区间和的积分等于各段积分和 :○3=⎰b
a dx x f )( .
● 微积分基本定理:一般地， ，并且 ，那么 ，这个结论叫做 ，又叫 .
为了方便起见，还常用()|b
a F x 表示()()F
b F a -，即 . ●常见基本函数的导数公式，求导法则，复合函数导数法则.(见课本)
二.讨论展示1，计算下列定积分: ⎰⎰⎰+----32220222)1()3(32)2()4)(24()1(dx x
x dx x x x dx x x １
2.计算下列定积分:
⎰⎰-461022cos )2()1(π
πxdx dx e x
(3)⎰31x dx 2。