有限自动机理论习题册-有限自动机原理
- 格式:pdf
- 大小:351.00 KB
- 文档页数:18



第三章有穷状态自动机软件开发环境国家重点实验室第三章有穷状态自动机习题:P126题1;题2 -1、2、3、4、5、6、9、10;题5;题7;题10 -1、2、3、4、5、6;题11;题14;题15;题20;题21思考题:题19、题24。
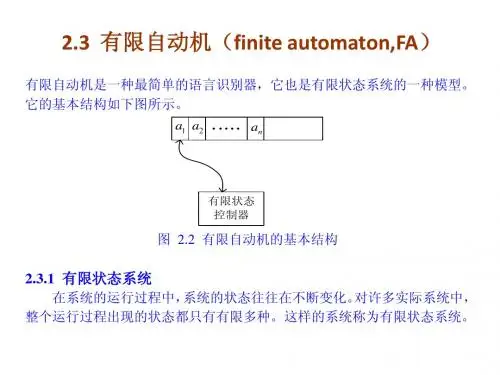
第三章有穷状态自动机一、有穷状态自动机FA 定义与表示二、确定的有穷自动机DFA三、非确定的有穷自动机NFA四、DFA 和NFA 的等价性五、带空移动的有穷自动机ε-NFA六、FA 是正则语言的识别器–FA 与RG 关系七、FA 的变形-带输出的FA3识别正则语言的有穷自动机(FA )模型实例:例:L (G )= { a n c | n ≧1 } ∪{ a n d | n ≧1 }。
一、有穷状态自动机定义与表示有穷状态自动机定义与表示识别语言自动机系统的结构及功能特征分析:1、字母表:系统处理的所有字符串由字母表上的字符组成;2、控制器:系统每次从输入字符串读入一个字符,并根据当前状态和读入的字符,转入新的状态;新的状态和当前状态可以相同也可不同;为此,系统具有有穷个状态,并需要维护一个读指针。
3、几个特殊状态:9一个开始状态;系统从此开始处理句子;9一些称之为终止状态或接受状态,系统从开始状态至此状态为止,读入字符构成的字符串是语言的一个句子;系统到达这些状态读入的全部字符串构成系统所能识别的语言。
有穷状态自动机定义与表示有穷状态自动机装置的物理模型:有穷状态自动机定义与表示有穷状态自动机装置的组成:1、一个具有一系列方格的输入字符串的带子:方格中存放字符,字符从输入带左端开始存放,输入带右端无穷;2、一个有穷状态控制器FSC:控制一个读头;每读入一个字符,读头右移一格,指向下一个待读入字符。
有穷状态控制器FSC 的基本工作过程:控制器执行动作由三个节拍组成:⑴读头读入当前指向的字符;⑵根据读入的字符和其自身当前状态,改变有穷状态控制器的状态;⑶读头右移一格指向下一个字符。

计算机组成原理与结构期末论文有限自动机的原理及示例学院:专业:姓名:学号:有限自动机的原理及示例本文将介绍几种重要有限自动机的基本原理,并通过例子说明它们的运行过程。
一. 语言的基本概念一张字母表是一个非空有限集合∑,字母表∑中的每个元素x 称为∑中的一个字母,也称符号、终止符或者字符。
∑中有限个字符1,,n a a 有序地排列起来12n x a a a =就称为∑上的一个字符串,n 称为它的长度。
其中有一个特殊的串ε,它的长度为零。
若1∑和2∑都是字母表,则它们的乘积12∑∑定义为{}12121122,a a a ∑∑=∈∑∈∑:a ,特别地, 0121{}n n ε-∑=∑=∑∑=∑∑∑=∑∑令*01kk k k ∞=∞+=∑=∑∑=∑若*,,x y z ∈∑,且z xy =则称,x y 是z 的子串。
字母表∑上的一种语言是*∑的一个子集L 。
二. 有限状态自动机的原理和运算实例1.基本原理一个有限状态自动机的物理模型通常包括两部分:(1)一个输入存储带,带被分解为多个单元,每个单元存放一个输入符号(字母表上的符号),整个输入串从带的左端点开始存放,而带的右端可以无限扩充。
(2)一个有限状态控制器(FSC ),该控制器的状态只能是有限个;FSC 通过一个读头和带上单元发生耦合,可以读出当前带上单元的字符。
初始时,读头对应带的最左单元,每读出一个字符,读头向右移动一个单元。
有限状态自动机的一个动作为:读头读出带上当前单元的字符;FSC 根据当前FSC 的状态和读出的字符,改变FSC 的状态;并将读头右移一个单元。
接着给出有限状态自动机的数学模型。
字母表∑上的一个有限状态自动机(FSAM)是一个五元组()0,,,,,FSAM Q q F δ=∑ 其中,i)Q 是一个有限状态的集合;ii)∑是字母表,它是输入带上的字符的集合;iii)0q Q ∈是开始状态;iv)F Q ⊂是接收状态(终止状态)集合;v):Q Q δ⨯∑→是状态转换函数,(,)q x q δ'=表示自动机在状态q 时,扫描字符x 后到达状态q '。






习题二十四1 给出接受下列在字母表{0,1}上的语言的确定的有限自动机:(a) 所有以00结尾的符号串的集合。
(b) 所有含有连续三个0的符号串的集合。
(c) 所有其任意五个连续符号中至少含有两个0的符号串的集合。
(d) 所有以1开头,并且若把它看成整数的二进制表示,它可以被5整除的符号串集合。
解:(a)分析:从初态读到0开始计数,若读到两个0则进入终态。
读到1则转向初态重新计数。
该DFA 如下图所示。
(b) 分析:从初态读到0开始计数,若读到连续三个0则进入终态。
进入终态后再读到0或1仍停留在终态。
其余状态读到1都转向初态重新计数。
该DFA 如下图所示。
(c )分析:根据题意,自动机必须考察任意连续的五个符号。
所以先画出所有含有五个符号的路径,将其中含有两个0的路径的最末端状态设为终状,例如,路径为00000的末端状态是非终态,而路径01011的末端状态为终态。
然后再从每条路径的最末端状态来考虑读入后续符号的状态转换。
例如,路径00000的末端状态读到0时,其路径仍然是00000,所以转换为其自身;而读到1时其路径为00001,则转换至路径00001的末端状态。
再如路径01011的末端状态读到0时,转换到路径10110的末端状态,这仍然是个终态;而读到1时,转换至路径10111的末端状态,这是一个非终态。
诸如此类推。
由于这个确定自动机的状态数量较大(共有64个状态),这里就不给出完整的自动机的图(d)分析:所有以0开头的符号串都不接受,设立一个死状态,开始读到0就进入死状态。
以1开头的符号串作为二进制数除5的余数可为:1,2,3,4,5。
每种余数为一种状态。
对应余数i 的状态在读到符号k 时的后继状态为(2i + k) mod 5。
如下图:2 请描述图24.1的转换图所给出的有限自动机所接受的集合。
解:根据该图状态转换关系可知,该有限自动机所接受的集合为字母表{0,1}上所有含有相同数目的0和1,并且任何前缀中0最多比1多一个且1最多比0多一个的符号串。
计算机组成原理与结构期末论文有限自动机的原理及示例学院:专业:姓名:学号:有限自动机的原理及示例本文将介绍几种重要有限自动机的基本原理,并通过例子说明它们的运行过程。
一. 语言的基本概念一张字母表是一个非空有限集合∑,字母表∑中的每个元素x 称为∑中的一个字母,也称符号、终止符或者字符。
∑中有限个字符1,,n a a 有序地排列起来12n x a a a =就称为∑上的一个字符串,n 称为它的长度。
其中有一个特殊的串ε,它的长度为零。
若1∑和2∑都是字母表,则它们的乘积12∑∑定义为{}12121122,a a a ∑∑=∈∑∈∑:a ,特别地, 0121{}n n ε-∑=∑=∑∑=∑∑∑=∑∑令*01kk k k ∞=∞+=∑=∑∑=∑若*,,x y z ∈∑,且z xy =则称,x y 是z 的子串。
字母表∑上的一种语言是*∑的一个子集L 。
二. 有限状态自动机的原理和运算实例1.基本原理一个有限状态自动机的物理模型通常包括两部分:(1)一个输入存储带,带被分解为多个单元,每个单元存放一个输入符号(字母表上的符号),整个输入串从带的左端点开始存放,而带的右端可以无限扩充。
(2)一个有限状态控制器(FSC ),该控制器的状态只能是有限个;FSC 通过一个读头和带上单元发生耦合,可以读出当前带上单元的字符。
初始时,读头对应带的最左单元,每读出一个字符,读头向右移动一个单元。
有限状态自动机的一个动作为:读头读出带上当前单元的字符;FSC 根据当前FSC 的状态和读出的字符,改变FSC 的状态;并将读头右移一个单元。
接着给出有限状态自动机的数学模型。
字母表∑上的一个有限状态自动机(FSAM)是一个五元组()0,,,,,FSAM Q q F δ=∑ 其中,i)Q 是一个有限状态的集合;ii)∑是字母表,它是输入带上的字符的集合;iii)0q Q ∈是开始状态;iv)F Q ⊂是接收状态(终止状态)集合;v):Q Q δ⨯∑→是状态转换函数,(,)q x q δ'=表示自动机在状态q 时,扫描字符x 后到达状态q '。
有限自动机例题有限状态自动机(FSA)是计算机科学中的一种重要数学模型,它在字符串匹配、语言解析和编译器设计等领域都有广泛应用。
本文将围绕一道有限自动机例题进行分析和讲解,以帮助读者深入理解有限自动机的本质和应用。
例题描述:假设有一个字符串集合S = {“hello”, “world”, “cherry”, “come”, “back”},请设计一个DFA(确定性有限状态自动机)匹配这些字符串。
其中,该DFA应该包含5个终止状态,也就是说,只有当输入符串是S中的某一个字符串时,该DFA才能停机并进入终止状态。
解题步骤:根据题目描述,我们需要设计一个DFA,能够匹配给定字符串集合S中的任意一个字符串。
下面是解题的详细步骤:1. 首先,我们需要确定该DFA的状态集合Q。
由于该DFA需要包含5个终止状态,所以我们可以将状态集合分为6个部分,其中5个部分分别对应于集合S中的5个字符串,另一个部分表示该DFA的非终止状态。
2. 接下来,我们需要确定该DFA的输入字母表,即该DFA可以接受哪些字符作为输入。
由于题目中给出的字符串集合只包含小写字母,所以我们将该DFA的输入字母表设为Σ = {a, b, c, ..., z},即从小写字母表中取任意一个字母作为输入。
3. 确定该DFA的转移函数δ。
对于这个例题,我们需要根据提供的字符串集合S,为每一个状态和每一个输入字符都分别指定一个转移关系。
例如,对于初始状态S0,若输入字符是“h”,则它应该转移到状态S1,若输入字符是其它字符,则应该一直停留在S0状态。
4. 建立该DFA的起始状态和终止状态集合。
由于该DFA需要同时接受集合S中的5个字符串,所以我们需要将对应的5个状态都设为该DFA的终止状态。
同时,我们将状态S0设为该DFA的起始状态。
5. 最后,我们需要测试该DFA的性能和有效性,确保它能够实现对给定字符串集合的匹配操作。
可以考虑用几个测试用例来验证该DFA的工作状态,例如输入hello、world、cherry等字符串,检查DFA是否能够正确识别这些字符串并停机。
习题三: 有限状态自动机1.构造有限状态机 {}3,2,1,0),,,,,,(===R S q g f R S Q M I 其中,对于2>t ,有)()()(t n t m t r +=这里⎩⎨⎧=02)(t m其它或是如果20)1(-t s⎩⎨⎧=01)(t n其它或是如果31)2(-t s如果0)0()1(==-s s ,确定)2(),1(r r 。
2.设{}c b a S ,,=,对于S 中每一符号s 和*S 中每一串ω,定义:ωω=)(s N 中s 出现的次数。
给出转换赋值机),,,,,(r q g f R S Q M =的状态图,对于输入串ω,它的最终输入出是5mod ))(3)(2)((ωωωc b a N N N r -+= 求激励是abbccbaabc 的响应。
3.已知有限状态机的状态图,写出相应的状态表。
图8-3.9图8-3.114.给定有限状态机的状态表,画出相应的状态图。
5.设M 是n 个状态的有限状态机,如果有一个激励,将M 从状态I q 转向状态q ,证明必存在一个长度小于n 的激励,使M 从状态I q 转向状态q 。
6.设计一台有限状态机M ,其中{}1,0==R S ,当输入串中有三个连续的0或1时,它输出1,其它均输出0。
7.设计一台有限状态机,其中{}b a S ,=,当且仅当输入符号串中包含两个连续的a 或两个连续的b 时,输出为1。
否则为0。
c c 11图8-3.10(b) (a) 0q1q 2qA B C D*8给定有限状态机1M 和2M 的状态图。
\证明a )当且仅当输入串是能被3整除的二进制数时,有限状态机1M 输出为1,其它为0。
b )当且仅当输入串是能被4整除的二进制数时,有限状态机2M 输出为1,其它为0。
1M 2M1图8-3.2。