第九--十一章 道路工程测量

由公式可得：T=68.72 L=135.10 E=7.77 D=2.34
1）放点
常用的方法有支距法和极坐标法两种。
如图所示,欲将图纸上定出的两段直线JD2~JD3和 JD3~JD4测设于实地，只需定出直线上1、2、3、4、5、 6等临时点即可,这些临时点可以选择支距也可选择极坐 标法测设。本图中采用支距法测设的为1、2、6三点。
即在图上以导线点D6、D7、D11为垂足,作导线边的垂线, 交路线中线点1、2、6为临时点,根据比例尺量出相应的 距离L1、L2、L6,在实地用经纬仪或方向架定出垂线方向, 再用皮尺量出支距,测设出各点。
本章主要介绍线路定测中的中线测量、纵横断面 测量和线路施工测量等内容。
第二节 道路中线测量
线路的中线测量就是通过直线和曲线测设，将 路中心线具体放样到地面上去。中线测量包括线路 的交点（JD）和转点（ZD）的测设，线路转角(α)的 测定，中线里程桩的测设，线路圆曲线测设等。道 路的平面线型如图：
一、交点和转点的测设
根据曲线测设的要求，在右角测定后，要求在不变动水
平度盘位置的情况下，定出角的分角线方向并钉桩标志 ，以
便将来测设曲线中点。设左盘测角时，后视方向的水平度盘
读数为a,前视方向的读数为b，分角线方向的水平度盘读数为
c。因 a b 则c的读数为
cb 或 c ab
2
2
此外，在角度观测后，还须用测距仪测定相邻交点间的 距离，以供中桩量距人员检核之用。
这种方法工作效率高，是用于测量控制点较少线路，缺点是 放线误差容易积累，因此一般连续放出若干个点后应与初测导线 点闭合，以检查误差是否过大，然后重新有初测导线点开始放出 以后的交点。方位角闭合差≤±40″，长度闭合差≤1/5000。

（1）在两交点间测设转点：
方法:
在JD5、JD6的大致中间位置ZD’架仪。瞄准
JD5，定出JD’6。
测量出a、b距离。 计算e值，实地量取e，得ZD点。有：e 在ZD点架仪，检查三点在一直线上。
a
a
b
f
（2）在两交点延长线上测设转点：
同理，计算出e值，实地量取e，得ZD点。有：
f abe a f
建筑工程测量—道路工程测量
一、道路工程测量概述
（一）勘测设计测量
初测 定测 1、初测内容:
控制测量、测带状地形图和纵断面图、收 集沿线地质水文资料、作纸上定线或现场定 线，编制比较方案，为初步设计提供依据。
三、交点JD的测设
（3）定交点
将直线延长，得交点JD。正倒镜分中法： 在B点架仪，盘左瞄准A，倒镜定a1，b1点；盘 右瞄准A点，倒镜定a2，b2点；取a1、 a2点中 点a， b1、b2点的中点b。 同理定出CD 方向上c、d两点。（骑马桩） 将线段ab、cd相交得交点JD。
三、交点JD的测设
2、拨角放线法——极坐标法 在利用导线点或已测设的JD，计算测设元素（β，
S）——拨角，量边，定出JD 位置。
四、转点ZD的测设
1、定义：当相邻两交点互不通视时，需要在其连 线测设一些供放线、交点、测角、量距时照准之 用的点。
2、分为： 在两交点间测设转点。
在两交点延长线上测设转点。
展开为
ci
li
l
3 i
24 R 2
ZY
i1 i
YZ
特点：
测点误差不积累。
宜以QZ 为界，将曲线 分两部分进行测设。
（2）短弦偏角法
与长弦偏角法相比： 1）偏角Δi相同。 2）计算曲线上各桩 点间弦线长ci 3）架仪于ZY或YZ 点，拨角、依次在 各桩点上在量边， 相交后得中桩点。

纵断面测量又称线路水准测量。它的任务是测定中线上各里程桩的地面高程，绘制中线纵断面图，作为设计线路坡度、计算中桩填挖尺寸的依据。 线路水准测量分两步进行：首先在线路方向上设置水准点，建立高程控制，称为基平测量；其次是根据各水准点高程，分段进行中桩水准测量，称为中平测量。基平测量的精度要求比中平高，一般按四等水准测量的精度；中平测量只作单程观测，按普通水准测量精度。 横断面测量是测定各中心桩两侧垂直于线路中线的地面高程，可供路基设计、计算土石方量及施工放边桩之用。 传统的路线纵、横断面测量是用水准仪进行，因此又称距线水准测量。现在又增加了全站仪和GPS的方法进行路线纵、横断面测量
在转折角 测定后， 定出其分角线方向C，在此方向上钉临时桩，以便日后测设线路曲线的中点。
里程桩（中桩）的设置
道路中线上除了交点和转点桩以外，还每隔一定距离设置里程桩。它的作用是：既详细标定了路线的位置和路线长度，又是施测路线纵、横断面的依据。 设置里程桩的工作主要是定线、量距和打桩。 各桩的桩号表示该桩距路线起点的里程，例如，某交点桩距路线起点的距离为3135.12m,其桩号为“JD3+135.12”。
中线测量
平面线型 由直线和曲线（圆曲线、缓和曲线）组成。
直线
圆曲线
缓和曲线
中线测量的概念
通过直线和曲线的测设，将道路中心线的平面位置测设到地面上，并测出其里程。即测设直线上、圆曲线上或缓和曲线上中桩。
ቤተ መጻሕፍቲ ባይዱ
路线的交点和转点测设
路线的各个交点是相邻直线段的相交之点。 交点（包括起点和终点）是详细测设道路中线的控制点。一般先在初测的带状地形图上进行纸上定线，设计交点的位置，然后实地测设交点位置。 转点是路线直线段上的点。定线测量中，当相邻两交点互不通视或直线段较长时，需要在其连线（直线段）上测定个或几个转点，以便在交点测量转折角和直线量距时作为照冷和定线的目标。路线直线段上，一般每隔200~300米设一转点，另外，在路线与其它道路交叉处以及路线上需设置桥、涵等构筑物处，也需要测设转点。

直 线 （m）
平原微 山岭重
丘区
丘区
≤50
≤25
曲
线（m）
不设超高 的曲线
R＞60
30＜R＜ 60
25
20
10
R＜30 5
特殊情况：如果设计需要或在地形变化处另设 整米加桩。
第32页/共152页
（一）偏角法测设圆曲线细部
偏角法是根据曲线点 i 的切线偏角δi及其间距c作 方向与距离交会，获得放样点位的。
K3+182.76 68.72
K3+114.04 67.55
K3+181.59 67.55
K3+249.14 68.72 2.34
k3+182.76 (计算无误)
第28页/共152页
三、圆曲线主点的测设
1、在交点位置已知情况下测设主点
交点JD2
★测设直圆点ZY ★测设圆直点YZ
直圆点ZY 交点JD1
α
切线长
T
外矢距1E80°-1α80-
曲中点QZ 2
切线长
T
圆直点YZ 交点JD3
★测设曲中点QZ
O
第29页/共152页
2、虚交点法测设圆曲线主点 1）圆外基线法
①选定副交点A、B， AB称圆外基线， 测量AB距离，测量转角αA、αB； ②计算A（JD）、B（JD）
③根据α、R计算T、L、E 并求出t1、t2。
ZD
ZDˊ ZD
出JD6´，丈量出JD6-JD6´=f，如f超过允许偏离范围，则须将测站ZD´横向移动至ZD
点，移动量e：
e a f ab
式中：a、b距离可直接丈量或用视距测出
第19页/共152页

《道路工程测量》课程标准一、前言（一）课程基本信息1.课程名称：道路工程测量2.课程类别：专业必修课3.课程编码：4.学时：605.适用专业：道路工程技术、道路工程监理等专业（二）课程性质本课程是道路工程专业重要的、具有较强实践性的的专业基础课。

本课程涵盖了道路工程施工过程中的全部测量工作内容。

通过本课程的学习，学生能承担道路工程测量员的职业岗位的工作。

（三）课程标准的设计思路1.课程设置的依据《道路工程测量》依据《杨凌职业技术学院关于课程标准制定及实施工作的通知》文件及附件（课程标准模版），按照岗位职能的要求，适当考虑工程单位近期的能力结构和技能要求，结合我院的具体情况，设计课程标准。

2.课程改革的基本理念：使课程内容的学习过程与道路工程测量的工作过程相一致，以学生职业能力的培养为目的选择课程学习的工作任务，在工作任务的设计上由简到繁，由实训到实操，形成理实一体化的课程教学。

⑴．课程教学内容以道路测量工作过程为导向。

整体教学内容的设计既符合以道路工测量的工作过程为导向，注重学生的职业能力培养，又符合知识的学习掌握过程。

⑵．课程设计以行动为导向突出学生主体地位。

整个教学过程以学生为主体，教师的作用在于设计适合训练学生专业能力的工作任务，提供相关专业知识、咨询信息，辅助引导学生更准确地完成工作任务的计划与实施。

并将实训工作任务的完成情况考核作为课程成绩评定的重要因素。

⑶．改革课程考核方式，注重能力本位的课程考核。

改变以往注重理论知识考核以及在课程结束后进行考核的方式，采用注重课程实践考核，在教学过程中对每一项实训工作任务进行考核，并将其考核成绩纳入课程考核成绩。

而且将仪器操作考核成绩与高级测量工考核相结合，作为课程考核的一部分。

二、课程目标或预期学习成果（一）总目标通过道路工程测量课程的学习，学生应达到道路工程高级测量员的技术要求，掌握道路工程施工过程中的全部测量工作及技术能力。

能承担道路工程、道路施工、路基施工、测量员的职业岗位，以及承担道路工程、道路设备施工员，道路监理员的主要专业技能之一。

D3
D1
JD 15 D2
(2)根据导线点的坐标和交点的设计坐标测设交点
按导线点的已知坐标和交点的设计坐标，事先算出有关测设 数据，按极坐标法，角度交会法或距离交会法测设交点，如下图 ，首先计算出A8到JD16之间的距离D，以及夹角β，然后用极坐 标法测设交点D16。
A7
A8
β A9
D
JD16
(3)穿线放线法测设交点
根据建设单位和规划院提供的水准点。用水准仪准确地引测到施 工现场附近便于监控的相应位置上，沿着道路方向，每隔100米 设置一个控制点，标注其绝对标高值。用于监控的水准点位置应 牢固稳定，不下沉、不变形。高程的引测应进行往返一个测回。 其闭合误差值不得大于3mm 。闭合误差值在允许范围内，可按水 平距离比例相应修正。建设单位所提供水准点及标高复测点应有 书面记录，并应有建设单位及监理单位现场代表签字认证。
当线路主点不能直接测设出、且定测中线离初测导线不
远时，常采用此方法。
(a) 放点 放点常用的方法有极坐标法和支距法。
1
2
3
l1
l2
β2
β1
4
l3 β3
5
极坐标法放点
4
5
l4
l5
7 6
支距法放点
(b)穿线
1Hale Waihona Puke A2穿线3
B
(c)交点：打“骑马桩”定交 点
c a
B
b JD
d C
A
D
转点的测设
转点 ZD定义：当相邻两交点互不通视时，需要在其连线 测设一些供放线、交点、测角、量距时照准之用的点。
1 设计道路
2
α3 α4
S1
S2

《道路工程测量》课程说明一、课程概述（一）课程性质《道路工程测量》是测绘、道桥工程技术专业的一门实践性、综合性较强的职业技能核心课程，该课程的建设将对数字测绘、数字道路的人才培养目标的实现起到关键作用。

本课程主要研究道路工程中各种测设方法，阐明工程质量要求及安全技术措施。

课程教学的目的是使学生掌握道路工程测量的基础知识、基本理论和决策方法，使学生具有解决道路工程测量的初步能力，并具备一定的实践操作技能，把学生培养成为理论知识与实践技能相结合的高级职业技术人才。

（二）课程定位根据测量员、施工员、安全员、质检员及相关岗位的任职要求，以及学生的认知及职业成长递进规律，在学习本课程前，必须会识图、绘图与审图，搞清道路上构筑物和建筑物的结构构造。

因此，其前置课程为：测绘CAD、工程监理、施工概预算等，它们是学好本门课程的必要基础。

同时本门课程又对后续的路面工程施工、施工组织与管理、道路工程招投标与合同管理等学习领域的课程学习起支撑作用，为这些课程的学习打下扎实的知识和技能基础。

（三）课程设计思路根据本专业的培养目标，我们邀请了施工企业一线工作的管理人员与专家一起来商讨、拟定岗位工作任务分析表。

在分析施工员、测量员、材料员、安全员等岗位的工作任务与职业能力的基础上。

并参照该岗位职业资格证书的考核要求。

确定该专业的核心能力，即较强的施工现场组织、管理和处理施工技术问题的能力。

以此我们确定了本课程的工作模块和课程内容，即按照道路工程施工的行业要求展开教学内容。

二、课程目标（一）课程工作任务目标掌握一般道路工程的常规测量方法、施工放样的基本原理；掌握一般道路施工测量的一些必要计算方法；熟悉一般道路施工测量中容易出现的常见质量、安全问题及质量、安全验收规范；熟悉一般道路工程施工测量的计算方法和操作技巧；了解国内外道路施工测量新技术和新动向及国家技术政策。

（二）职业能力目标能根据施工图纸和施工实际条件，选择和制定常规工程合理的施工方案；能查找资料和完成施工中遇到的一些必要测量计算；能根据道路工程质量验收方法及验收规范进行常规工程的施工测量；能正确运用道路工程测量技术标准合理安排、协调道路工程施工。

§11-５ 带有缓和曲线的平曲线测设
一、缓和曲线
㈠缓和曲线的概念 在直线与圆曲线之间插入的一段曲率半径由无穷大逐渐变 化到圆曲线半径R的过渡性曲线。以适应行车轨迹、消除离心 力突变及满足超高和加宽的过渡要求。
我国公路、铁路设计，采用回旋线作为缓和曲线。
㈡缓和曲线公式 1.基本公式 回旋线是曲率半径随曲线长度增加而成反比均匀减小的曲 线。
xi=Rsinφi yi=R（1－cos φi）
y
O φi R
式中：i
li R
180
xi
Pi
li
yi
ZY（或YZ）
X（JD）
2.偏角法：以ZY（YZ或）点至曲线上任一点Pi的弦 线与切线间的偏角Δi来确定Pi位置的方法。
JD
i
i
2
li
180
2
ci
2R sin i
2
2R sin
li 2R
QZ里程 ＋ D/2
JD里程（计算检核）
3.圆曲线主点的测设方法
JDi架仪，照准JDi-1，量取T，得ZY点； 照准JDi+1，量取T，得YZ点； 在分角线方向量取E，得QZ点。
例题：某路线JD桩号为k4+390.78，转角 α=12°30′，圆曲线半径R=500m，试计算圆曲线 元素及各主点里程。
y R 1 cos p
X X ZHi x cos Ai1、i y sin Ai1、i Y YZHi x sin Ai1、i y cos Ai1、i
X
ZHi-1
Ai-1、i
JDi-1
HZi-1
JDi
x
ZHi
HYi QZi YHi
HZi ZYi+1

结论和要点
测量在道路工程中起着关键的作用，帮助确保道路建设的准确性和质量。通过正确选择和应用测量工具、 技术和方法，可提高项目效率和成功率。
遥感测量法
使用卫星图像和航空摄影图 像，获取大范围的地理信息 和地物特征。
计算和分析测量数据
1
数据收集
使用测量仪器和工具，采集准确的测量数据并记录。
2
数据处理
对收集的数据进行计算和分析，验证其准确性和可靠性。
3
数。
道路工程测量的实际应用
道路规划
测量工具和仪器
测量尺
用于测量线段和曲线的长度和 高度。
全站仪
用于测量地形和建筑物的位置 和高度。
经纬仪
用于测量方位角和俯仰角，以 确定目标的位置。
测量技术和方法
三角测量法
通过测量三角形的边长和角 度，计算其它目标的距离和 位置。
现场测量法
利用实地测量和标志物测量 的方法，获取道路工程的实 际尺寸和位置数据。
《道路工程测量测量》 PPT课件
测量在道路工程中扮演着重要的角色。本课件将详细介绍测量的定义和目的， 测量工具和仪器的使用，各种测量技术和方法，以及如何计算和分析测量数 据。
测量的定义和目的
测量是一种确定和记录物体或地区真实尺寸、形状和地理位置的方法。在道路工程中，测量的目的是确 保道路的准确施工和质量控制。
测量用于确定最佳道路路线和交通规划。
施工监测
测量用于监测道路施工过程中的变形和偏差。
道路维护
测量用于评估道路损坏和制定维护计划。
交通流分析
测量用于分析道路交通流量和拥堵情况。
测量误差和精度控制
测量过程中存在误差，因此精确控制误差和提高测量精度非常重要。使用校准工具和技术可以减小误差， 并确保测量结果的准确性。

第二节 道路中线测量
主点桩号计算无误 （3）主点测设
将经纬仪安置在交点（JD）上，后视相邻交点或转点，沿视线方向量取 切线长度，得曲线起点（ZY），并检查ZY点至相邻里程桩的距离，较差应在限 差之内后并打桩。再将望远镜瞄准前视方向的交点或转点，沿此方向量切线长 度，得曲线终点（YZ）。最后沿分角线方向量取外矢距，得到曲线中点（QZ） 点。 2.圆曲线的详细测设
。因
，则
第二节 道路中线测量
图9-8
图9-9
三、里程桩的设置
为了确定线路中线的具体位置和线路长度，满足线路纵横断面测量以及为
线路施工放样打下基础，则必须由线路的起点开始每隔20ｍ或50ｍ（曲线上根据不
同半径每隔20ｍ、10ｍ或5ｍ）钉设木桩标记，称为里程桩。桩上正面写有桩号，
背面写有编号，桩号表示该桩至线路起点的水平距离。如某桩至路线起点距离为
第九章 道路工程测量
用视距法测出a、b，则ZD´应横向移动的距离e可按下式计算：
e a f ab
将ZD´ 按e值移至 ZD。
（9-2）
第二节 道路中线测量
图9-7
第九章 道路工程测量
二、转角的测定
线路从一个方向转向另一个方向时，偏转后的方向与原方向间的夹角称为 转角，用 表示。在线路的转弯处一般要求设置曲线，而曲线的设计要用到转角， 所以，设计前必须测设出转角的大小。
本章主要介绍线路定测中的中线测量、纵横断面测量和线路施工测量等内容。
第一节 概述
第二节 道路中线测量
第九章 道路工程测量
线路的中线测量就是通过直线和曲线测设，将路中心线具体放样到地面上 去。中线测量包括线路的交点（JD）和转点（ZD）的测设，线路转角(α)的测 定，中线里程桩的测设，线路圆曲线测设等。道路的平面线型如图9-1：

第十一章道路工程测量道路工程测量§11-1 道路工程测量概述初测――在路线可能范围内，测回带状地形图、纵断面图，收集地质、水文等资料，为初步设计提供依据。

定测――在选定设计方案的路线上进行中线测量、纵、横断面测量、带状地形图测绘。

§11-2 道路中线测量一、交点和转点的测设(一)交点测设1、根据地物测设交点a JDb c§11-2 道路中线测量(一)交点测设2、根据导线点测设交点A sJD(P) Bs ( x p xa ) ( y p y a )ap arctany p ya x p xaap ab§11-2 道路中线测量(一)交点测设3、穿线法测设交点B JDCAD§11-2 道路中线测量(二)转点测设1、两交点间设转点a e f a bJD1 ab JD2ef§11-2 道路中线测量二、路线转折角的测定右左右180 前进方向左180三、里程桩的设置里程桩的作用标定路线中线的位置和长度测量路线纵、横断面的依据§11-3 道路圆曲线的测设一、圆曲线主点的测设(一)主点测设元素的计算T R tan 2 L R 180 R 1 E R R( 1) cos cos 2 2 J 2T L§11-3 道路圆曲线的测设一、圆曲线主点的测设(二)主点桩号的计算ZY桩号JD桩号T L QZ桩号ZY桩号2 L YZ桩号QZ桩号2 检核YZ 桩号=JD桩号+T-J§11-3 道路圆曲线的测设一、圆曲线主点的测设(三)主点的测设1.曲线起点的测设经纬仪安置在JD点，后视相邻交点，量切线长T,即为ZY 点。

2.曲线终点的测设经纬仪，前视相邻交点，量切线长T,即为YZ 点。

3.曲线中点的测设测定路线转折角的分角线方向(曲线中点方向),量外距E,即为QZ点§11-3 道路圆曲线的测设二、圆曲线主点的详细测设(一)偏角法§11-5路线纵、横断面测量一、路线纵断面测量(一)基平测量-------控制测量(同四等水准测量) (二)中平测量-------逐个测定中桩的地面高程§11-5路线纵、横断面测量一、路线纵断面测量(三)纵断面图的绘制及施工量计算§11-5路线纵、横断面测量二、路线横断面测量(一)测设横断面方向§11-5路线纵、横断面测量二、路线横断面测量(一)测设横断面方向§11-5路线纵、横断面测量二、路线横断面测量(一)测设横断面方向§11-5路线纵、横断面测量二、路线横断面测量(二)测定横断面上点位 1.水准仪皮尺法§11-5路线纵、横断面测量二、路线横断面测量(二)测定横断面上点位 2.标杆皮尺法§11-5路线纵、横断面测量二、路线横断面测量(二)测定横断面上点位 3.经纬仪视距法经纬仪安置于中桩上,定出横断面方向,量出仪器高,用视距法测出各特征点与中桩的距离和高差。

备注
1.006
516.661
513.499 516.16 516.14 515.84 515.46 515.65
BM1高程为 基平所 测 基平测得 BM2高 程为 524.82 4
517.386
…
515.140
…
2.32
523.06
BM2
0.606
524.782
图形：水准仪中平测量（例题）
0+000
同学们好！
欢迎来到
第11章 路线纵、横断面测量
在本章，您将要学习道路纵、横断面
测量，进行基平、中平、跨沟谷测量及 成果处理，纵、横断面及地面线的绘制。
第11章 路线纵、横断面测量
路线纵断面测量：又称中线高程测量，它的 任务是 在道路中线测定之后，测定中线各里程桩的 地面高程，供路线纵断面图点绘地面线和设 计纵坡之用。 路线纵断面高程测量采用水准测量。纵断面 测量可分为基平测量和中平测量。
测站2
一、中平测量的方法
0+000
测站3
测站1 基平测量获得
中视最远距离150 ；中视距离读到
位
§11.2 中平测量
一、中平测量的方法 中平测量只作单程测量。一测段观测结束后，应 计算测段高差。它与基平所测测段两端水准点高 差之差，称为测段高差闭合差。 中桩高程测量的精度要求，其容许误差：高速公 路、一级二级公路为± 30 L mm； 三级、四级公路为 50 mm 。 L 每一测站的计算按下列公式进行： 视线高程=后视点高程+后视读数 中桩高程=视线高程－中视读数 转点高程=视线高程－前视读数
2.246 2.246 … …
水准尺读数（m） 后视 2.191 1.62 1.90 0.62 2.03 0.90 3.162 0.50 0.52 0.82 1.20 1.01 1.521

道路工程在勘测设计、施工建造和运营管理各阶段中所进行的测量工作总称为路线测量。

道路工程测量的主要任务包括以下几方面：(1)控制测量：根据道路工程的需要，进行平面控制测量和高程控制测量。

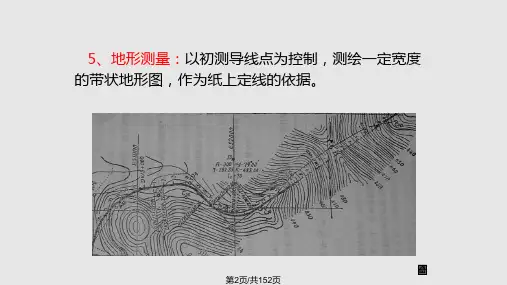
(2)地形图测绘：根据设计需要，实地测量道路附近的带状地．．．形．图．。

(3)中线测量：按照设计要求将道路位置测设与实地。

(4)纵、横断面图测绘：测定道路中心线方向和垂直于中心线方向的地面高低起伏情况，并绘制纵、横断面图。

(5)施工测量：按照设计要求和施工进度及时放样各种桩点作为施工依据。

此外，有些道路工程还需要进行竣工测量、变形检测等。

根据方案研究阶段在已有地形图上规划的道路位置，结合实地情况，选择交点和转点的位置并插旗，标出道路走向的大概位置，为导线测量和各专业调查指出行进方向。

导线控制测量是测绘道路带状地形图和定线、放线的基础，导线应全线贯通。

采用全站仪或者光电测距仪观测导线边长时，导线点间距普通为1km，但应在不长于500m 处设置加点。

采用光电测距仪传递高程时，导线边长宜在200~600m 之间。

由于导线延伸很长，为了检核导线的精度并统一坐标，必须设法与国家平面控制点或者GPS 点进行联测。

随着测量仪器设备的发展，导线测量越来越多的使用GPS 和全站仪配合施测。

从起点开始沿道路方向直至终点，每隔5km 摆布布设GPS 对点 (每对GPS 点间距300~400m)，在GPS 对点之间按规范要求加密导线点。

用全站仪测量相邻导线点间的变长和角度，之后使用专业测量软件进行导线精度校核及成果计算，最终获得各导线点的坐标。

导线的观测包括转折角的观测和导线边的观测及导线点高程测量。

①转折角的观测转折角的观测普通采用测回法进行。

在进行国家等级转折角观测时，应以奇数测回和偶数测回分别观测导线前进方向的左角和右角；在进行一、二级和三级导线转折角观测时，普通应观测前进方向的左角。

对于闭合导线，若按逆时针方向进行观测，则观测的导线角既是闭合多边形的内角，又是导线前进方向的左角。

道路工程测量作业指导书标题：道路工程测量作业指导书引言概述：道路工程测量是道路建设过程中不可或者缺的环节，准确的测量工作可以保证道路工程的质量和安全。

本文将为道路工程测量作业提供指导，匡助工程师们更好地进行测量工作。

一、测量前准备工作1.1 确定测量目的：在进行测量前，需要明确测量的目的，例如道路设计、施工等。

1.2 准备测量工具：包括测距仪、水准仪、全站仪等，确保工具的准确性和完好性。

1.3 制定测量计划：根据测量目的和具体情况，制定详细的测量计划，包括测量路线、测量方法等。

二、测量现场操作2.1 确定基准点：在测量现场确定基准点，确保测量的准确性和一致性。

2.2 进行测量：按照测量计划和方法进行实际测量操作，注意测量过程中的误差和校正。

2.3 记录数据：及时记录测量数据，包括测量点坐标、高程等信息，确保数据的完整性和准确性。

三、数据处理与分析3.1 数据处理：对测量得到的数据进行处理，包括数据清洗、校正等操作，确保数据的准确性。

3.2 数据分析：根据处理后的数据进行分析，得出测量结果，如道路线型、坡度等信息。

3.3 数据报告：将测量结果整理成报告形式，包括测量数据、分析结果等内容，便于后续工作的参考和使用。

四、质量控制与验收4.1 质量控制：在测量过程中进行质量控制，包括数据校核、误差分析等操作，确保测量结果的准确性。

4.2 验收工作：对测量结果进行验收，与设计要求进行比对，确保测量结果符合要求。

4.3 整改与完善：根据验收结果进行整改和完善工作，保证测量结果的质量和可靠性。

五、安全注意事项5.1 安全意识：在进行测量工作时，要时刻保持安全意识，避免发生意外事故。

5.2 保护设备：在使用测量工具时，要注意保护设备，避免损坏或者丢失。

5.3 环境保护：在测量现场要注意环境保护，避免对周围环境造成污染或者破坏。

结论：道路工程测量是道路建设过程中至关重要的环节，准确的测量工作可以保证道路工程的质量和安全。