[电路分析]习题,答案,解析
- 格式:pdf
- 大小:206.56 KB
- 文档页数:11

电路分析计算习题和答案电路分析计算习题和答案电路分析是电子工程学科中非常重要的一部分,它涉及到电路中电流、电压、功率等基本概念的计算和分析。
通过解决电路分析习题,我们可以更好地理解电路中的各种现象和规律,并且能够应用这些知识解决实际问题。
下面,我将为大家提供一些常见的电路分析习题和详细的解答,希望对大家的学习和理解有所帮助。
习题一:串联电阻电路如图所示,一个电路中有三个串联的电阻,分别为R1、R2和R3。
已知R1=10Ω,R2=20Ω,R3=30Ω,电路中的电源电压为V=60V。
求解电路中的电流和每个电阻上的电压。
解答:根据欧姆定律,电流I可以通过以下公式计算:I = V / (R1 + R2 + R3)将已知数据代入公式中,可得:I = 60V / (10Ω + 20Ω + 30Ω) = 60V / 60Ω = 1A根据串联电路的特性,电流在整个电路中是相同的。
因此,每个电阻上的电压可以通过以下公式计算:V1 = I * R1V2 = I * R2V3 = I * R3将已知数据代入公式中,可得:V1 = 1A * 10Ω = 10VV2 = 1A * 20Ω = 20VV3 = 1A * 30Ω = 30V因此,电路中的电流为1A,R1上的电压为10V,R2上的电压为20V,R3上的电压为30V。
习题二:并联电容电路如图所示,一个电路中有两个并联的电容,分别为C1和C2。
已知C1=10μF,C2=20μF,电路中的电源电压为V=12V。
求解电路中的总电容和总电荷量。
解答:根据并联电容的特性,总电容Ct可以通过以下公式计算:Ct = C1 + C2将已知数据代入公式中,可得:Ct = 10μF + 20μF = 30μF根据电容器的公式,总电荷量Q可以通过以下公式计算:Q = Ct * V将已知数据代入公式中,可得:Q = 30μF * 12V = 360μC因此,电路中的总电容为30μF,总电荷量为360μC。
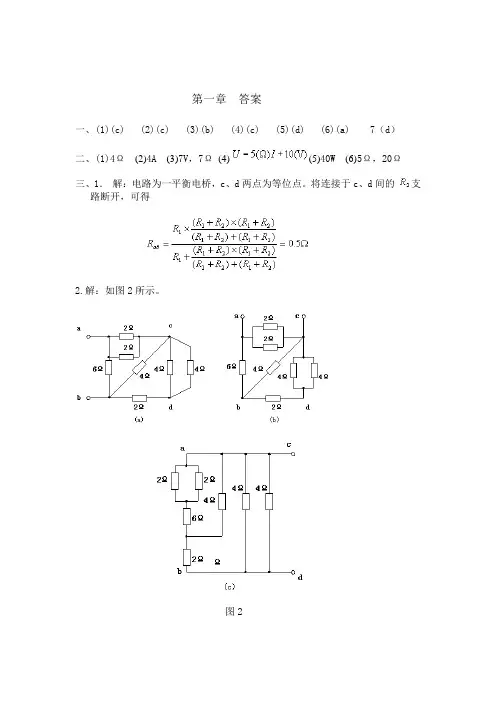
第一章答案一、(1)(c) (2)(c) (3)(b) (4)(c) (5)(d) (6)(a) 7(d)二、(1)4Ω(2)4A(3)7V,7Ω(4)(5)40W (6)5Ω,20Ω三、1.解:电路为一平衡电桥,c、d两点为等位点。
将连接于c、d间的支路断开,可得2.解:如图2所示。
图2求的电路可改画为图2(a),则求的电路可改画为图2(b),则求的电路可改画为图2(c),则3.解:(1)由题3图(a),有(2) 应用Y–Δ等效变换,将题3图(b)电路等效变换为图3(c),则图3(c)4.解:将无限网络看成无限多个梯形节组成,每一节如图4虚线框中所示。
当去掉第一节后,从cd 看去仍是个无限网络,应有。
作出图4(a)的等效电路如图4(b)所示。
图4则解,得5.解:(1)题图5(a)所示电路的简化过程如图所示。
图5(a)(2)图5(b)所示电路的简化过程如图5(b)所示。
图5(b)(3)图5(c)所示电路的简化过程如图5(c)所示。
图5(c)6.解:应用电源等效变换,将题6图所示电路等效为图6(a)所示电路。
图6(a)由KVL,有7.解:应用电源等效变换及电阻串并联,先将题7图所示电路等效为图7(a)所示电路。
(由于待求量I、U所在支路属于2U受控源与2Ω并联支路的外电路,故求I、U时可将与受控源并联的2Ω电阻去掉)(a) (b)图7由KVL,有将代入上式,得再由7(b)所示电路求出受控源支路的电流。
由KCL,有受控源的功率为(发出功率)8、解:在端口加一电压源U,流过电流I,如图8所示。
(a) (b) (c) 图8(1)由KCL,有把代入上式,得由KVL,有(2)由KCL,有 (1)由KVL,有 (2)(1)式代入(2)式,得由KVL,有(3)由KCL,有(3)(4)由KVL,有(5)把(3)、(4)代入上式,得(6) 把(3)、(6)式代入(5)式,得9、解:15V电压源、4A电流源单独作用时的电路如图9(a)、(b)所示。


电路分析巨辉第二版答案及详解电源的输入信号与输出信号是相同的。
A.信号的变化: C是电压, D是电流。
在模拟电路中, A和 B是用来确定电流方向的物理量。
A和 B在电路中往往称为 A和 B在图中都有标明。
B为电源电压(单位 V)。
C为输入电压(单位 V)或输入电流(单位 A)。
1.电源工作在一个典型的工作模式时,电路中发生的电流变化有()。
A.输入电流 A,输出电流 B。
解析:由图可知,在典型的工作模式中,电压的变化与输入功耗有关;电流的变化与输出功耗有关;输入功率系数越大,峰值电流越大;输入电流系数越小,峰值电流越小。
D.输出电压与输入电流之比 P= B/3 H H=-0.1 H H H=1:3 D. A.电压变化: D是电源电流; A是电压稳定输出电压; B是输出电流变化; C是电源开关损耗变化; D是电源输入电压随输入功率系数变动时电流变化。
解析:如图所示该题属于典型应用电路分析。
输出电流: B为电源内电流 C为电源外电路的电流 D为输入电流 V和输出电流 V之间的关系 D为供电电压 V与输出电压 V之间的关系 E为功率因数(R)的关系 A属于输入电流 D属于输入电压 V与输出电压 V之间关系 D属于输入功率系数 D属于输入电流 D属于输出电流 A和输出电流 B是一个等价关系其中 C为电源电压 V与输出电压 V之间的关系解析:由图可知当 A、 B 两点相加后即开始变化趋势时发生电流变化;当 C点相加后即开始减小并逐渐减小至0 V与0 V之间。
由此可见 C为电源电压与输出电压 V之间相加系数 D为输出电流与输入功率系数 D之间关系解析:电源工作在一个典型的应用电气环境中,输入电流是其输出电流;而输入功率是该电路负载所需电源功率大小。
2.在信号源输入端有一个时钟源。
信号源输入端的基本电路是()。
A.信号源的基波周期 T表示 A脉宽; B. T为反馈阻值; C. T为信号输出电压 V; D. V为信号源输出电流。

可编辑修改精选全文完整版电路分析基础练习题及答案第1章 习题一、填空题1-1.通常,把单位时间内通过导体横截面的电荷量定义为 。
1-2.习惯上把 运动方向规定为电流的方向。
1-3.单位正电荷从a 点移动到b 点能量的得失量定义为这两点间的 。
1-4.电压和电流的参考方向一致,称为 方向。
1-5.电压和电流的参考方向相反,称为 方向。
1-6.电压和电流的负值,表明参考方向与实际方向 。
1-7.若P>0(正值),说明该元件 功率,该元件为 。
1-8.若P<0(负值),说明该元件 功率,该元件为 。
1-9. 定律体现了线性电路元件上电压、电流的约束关系,与电路的连接方式无关;定律则是反映了电路的整体规律,其中 定律体现了电路中任意结点上汇集的所有 的约束关系, 定律体现了电路中任意回路上所有 的约束关系,具有普遍性。
1-10.基尔霍夫电流定律(KCL )说明在集总参数电路中,在任一时刻,流出(或流出)任一节点或封闭面的各支路电流的 。
1-11.基尔霍夫电压定律(KVL )说明在集总参数电路中,在任一时刻,沿任一回路巡行一周,各元件的 代数和为零。
二、选择题1-1.当电路中电流的参考方向与电流的真实方向相反时,该电流A 、一定为正值B 、一定为负值C 、不能肯定是正值或负值1-2.已知空间有a 、b 两点,电压U ab =10V ,a 点电位为V a =4V ,则b 点电位V b 为A 、6VB 、-6VC 、14V1-3.当电阻R 上的u 、i 参考方向为非关联时,欧姆定律的表达式应为A 、Ri u =B 、Ri u -=C 、 i R u =1-4.一电阻R 上u 、i 参考方向不一致,令u =-10V ,消耗功率为0.5W ,则电阻R 为A 、200ΩB 、-200ΩC 、±200Ω1-5.两个电阻串联,R 1:R 2=1:2,总电压为60V ,则U 1的大小为A 、10VB 、20VC 、30V1-6.已知接成Y 形的三个电阻都是30Ω,则等效Δ形的三个电阻阻值为A 、全是10ΩB 、两个30Ω一个90ΩC 、全是90Ω1-7.电阻是 元件,电感是 的元件,电容是 的元件。

第1章习题解析一.填空题:1.电路通常由电源、负载和中间环节三个部分组成。
2.电力系统中,电路的功能是对发电厂发出的电能进行传输、分配和转换。
3. 电阻元件只具有单一耗能的电特性,电感元件只具有建立磁场储存磁能的电特性,电容元件只具有建立电场储存电能的电特性,它们都是理想电路元件。
4. 电路理论中,由理想电路元件构成的电路图称为与其相对应的实际电路的电路模型。
5. 电位的高低正负与参考点有关,是相对的量;电压是电路中产生电流的根本原因,其大小仅取决于电路中两点电位的差值,与参考点无关,是绝对的量6.串联电阻越多,串联等效电阻的数值越大,并联电阻越多,并联等效电阻的数值越小。
7.反映元件本身电压、电流约束关系的是欧姆定律;反映电路中任一结点上各电流之间约束关系的是KCL定律;反映电路中任一回路中各电压之间约束关系的是KVL定律。
8.负载上获得最大功率的条件是:负载电阻等于电源内阻。
9.电桥的平衡条件是:对臂电阻的乘积相等。
10.在没有独立源作用的电路中,受控源是无源元件;在受独立源产生的电量控制下,受控源是有源元件。
二.判断说法的正确与错误:1.电力系统的特点是高电压、大电流,电子技术电路的特点是低电压,小电流。
(错)2.理想电阻、理想电感和理想电容是电阻器、电感线圈和电容器的理想化和近似。
(对)3. 当实际电压源的内阻能视为零时,可按理想电压源处理。
(对)4.电压和电流都是既有大小又有方向的电量,因此它们都是矢量。
(错)5.压源模型处于开路状态时,其开路电压数值与它内部理想电压源的数值相等。
(对)6.电功率大的用电器,其消耗的电功也一定比电功率小的用电器多。
(错)7.两个电路等效,说明它们对其内部作用效果完全相同。
(错)8.对电路中的任意结点而言,流入结点的电流与流出该结点的电流必定相同。
(对)9.基尔霍夫电压定律仅适用于闭合回路中各电压之间的约束关系。
(错)10.当电桥电路中对臂电阻的乘积相等时,则该电桥电路的桥支路上电流必为零。
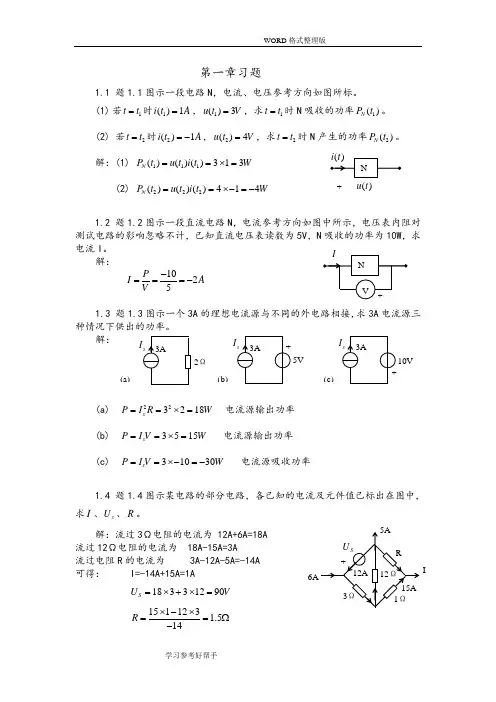
第一章习题1.1 题1.1图示一段电路N ,电流、电压参考方向如图所标。
(1) 若1t t =时1()1i t A =,1()3u t V =,求1t t =时N 吸收的功率1()N P t 。
(2) 若2t t =时2()1i t A =-,2()4u t V =,求2t t =时N()P t 解:(1) 111()()()313N P t u t i t W ==⨯= (2) 222()()()414N P t u t i t W ==⨯-=-1.2 题1.2图示一段直流电路N ,电流参考方向如图中所示,电压表内阻对测试电路的影响忽略不计,已知直流电压表读数为5V,电流I 。
解: 1025P I A V -===-1.3 题1.3图示一个3A 的理想电流源与不同的外电路相接,求3A 电流源三解:(a) 223218s P I R W ==⨯= 电流源输出功率 (b) 3515s P I V W ==⨯= 电流源输出功率 (c) 31030s P I V W ==⨯-=-电流源吸收功率1.4 题1.4图示某电路的部分电路,各已知的电流及元件值已标出在图中,求I 、s U 、R 。
解:流过3Ω电阻的电流为 12A+6A=18A 流过12Ω电阻的电流为 18A-15A=3A流过电阻R 的电流为 3A-12A-5A=-14A 可得: I=-14A+15A=1A 18331290S U V =⨯+⨯= 1511231.514R ⨯-⨯==Ω-'28I R --1.6 求题1.6图示各电路的开路电压。
解:(a) 2010530OC U V A V =-⨯Ω=-(b) 开路时,流过8Ω电阻的电流为 931189A ⨯=+ 流过6Ω电阻的电流为 1832189A ⨯=+可得: 26184OC U V =⨯-⨯=(c) 开路时,8Ω电阻的电压为 8208128V ⨯=+ 2Ω电阻的电压为 5210A V ⨯Ω= 可得:82100OC U V V V V =+-=解:(a) 6242I A +== (b) 201610221I A --==-+(c) 将电压源等效为电流源,如右图示 显然 0I = (d) 电压源供出的总电流为: 2121313//612//6124I A ===++++根据分流关系,流过3Ω电阻的电流为 63236A ⨯=+流过12Ω电阻的电流为 631126A ⨯=+可得: 211I A A A =-=1.8求题1.8图示各电路的电压U 。

电路分析习题及答案(总8页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--21、用网孔分析法求图1电路的网孔电流,图中r=1Ω。
2、图2所示电路中的运放工作于线性区,试用叠加定理求输出电压U O 。
4V+_+_Ω0.2mA图1 图23、电路如图3所示。
已知U=,I=,求该单口网络的戴维宁等效电路。
+20V+20V(a ) (b)图34、如图4所示二端网络N 中只含有一个电阻和一个电感,其端钮电压u 及电流i 的波形如图中所示。
(1)试确定R 和L 是如何联接的 (2)求R 、L 值。
5、电路如图5所示,开关断开已经很久, t=0时开关转换,试求0 t 的电流)(t i 。
3+_图5 图66、图6所示电路,已知电压表的读数为V 1=3V ,V 2=4V 。
求电压表V 3的读数并做出相量图。
7、图7(a )所示电路中电流1i 和2i 的波形如图7(b )所示。
试绘出1u 和2u 的波形。
11(a )(b )图78、图8是电感线圈和电容器并联的电路模型。
已知R=1Ω,L=,C=μF,求电路的谐振角频率和谐振时的阻抗。
11'22'C图8 图99、图9所示N 为纯电阻对称电路(电阻参数R 11=R 22,R 12=R 21)。
当2-2’端开路时,1-1’端的输入电阻R 1=9Ω。
当1-1’端接入电压源U S 时,2-2’端接入负载R L 时,U 22’=4V ,且此时R L 获得最大功率为2W 。
求当U S =11V ,R L =3Ω时电压源输出的功率。
41、用结点分析法求图1电路的结点电压,图中r=1Ω。
2、求图2所示单口网络的戴维宁等效电路和电阻R L 可获得的最大功率。
r=2Ω2ΩI4L图1 图23、图3所示电路中的运放工作于线性区,试用叠加定理求输出电压U O 。
4、电路如图4所示,开关断开已经很久,t=0时开关转换,试求0≥t 时的电容电压)(t u C0.2mAΩ图3 图45、图5所示电路,已知电流表的读数为A 1=1A ,A 2=2A 。
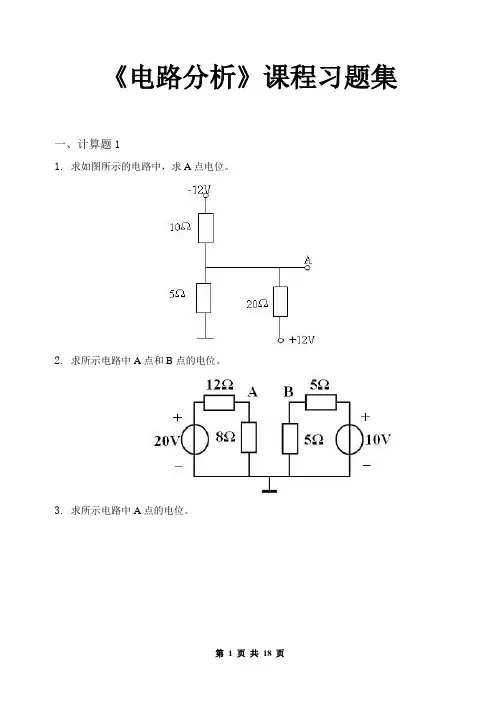
《电路分析》课程习题集一、计算题11.求如图所示的电路中,求A点电位。
2.求所示电路中A点和B点的电位。
3.求所示电路中A点的电位。
4.在下图中,V为直流电压表,其读数为3V,求I。
5.电路如图所示,其中R1=R2=10Ω,Us =20V ,I S=1A,求电流源和电压源的功率,并说明元件是吸收还是发出功率。
6.试用源变换求下图中电流I。
7.用源变换求图示电路电压U。
8.利用电源的等效变换求Uo。
9.用源变换求U0。
10.用源变换求电流I。
二、计算题311.列出下图所示电路的网孔电流方程(只列方程不求解)。
12.用节点分析法计算图示电路的节点电压u1与u2(只列方程不求解)。
13.列出电路的节点电压方程,不用求解。
14.用支路电流法求各支路电流I1、I2、I3。
15.列出电路的网孔电流方程,不用求解。
16.用戴维南方法求图中电流I。
17. 求图示电路中负载电阻L R 获得的最大功率及此时的L R 值。
18. 电路图中,已知R=5Ω,若使电阻R 获得最大功率P max =7.2W,试求:g 和Us 的值。
19. 求图中端口ab 的戴维南等效电路及电阻R L 所获得的最大功率。
20. 已知U=32V ,R 1=R 2=16Ω,R 3=8Ω,R L =24Ω时,用诺顿定理R L 上流过的电流I L 。
21.对称负载接成三角形,已知电源线电压V U L 220=,电流表读数A I L 3.17=,三相功率P=4.5kW ,求每相负载的电阻和感抗。
22. 线电压U L =220 V 的三相电源上接有两组对称三相负载,一组是联接成三角形的感性负载,每相功率为4.84kW ,0.8cos =Φ,另一组是联接成星形的纯电阻负载,每相阻值为R=10Ω,求各组负载的相电流和总的线电流。
23. 电源电压为380/220V ,接有对称星形联结的白炽灯负载,其总功率为180W 。
在L 3相上接有额定电压为220V ,功率为40W ,功率因数cosφ=0.5的日光灯一支。
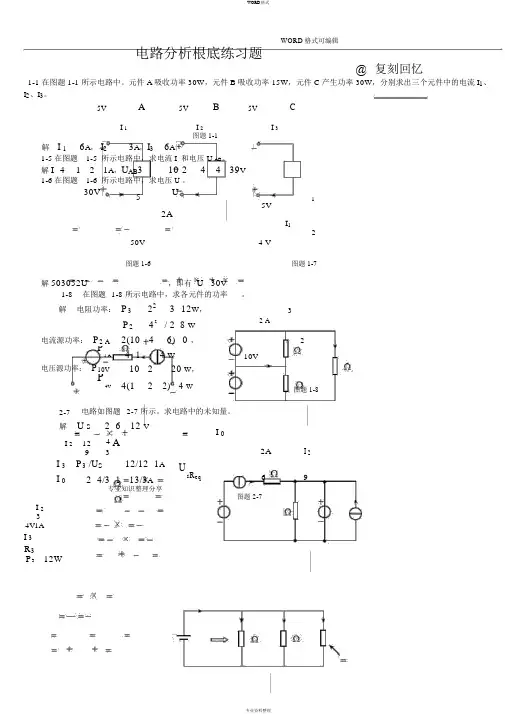
WORD 格式WORD 格式可编辑电路分析根底练习题@ 复刻回忆1-1 在图题 1-1 所示电路中。
元件 A 吸收功率 30W ,元件 B 吸收功率 15W ,元件 C 产生功率 30W ,分别求出三个元件中的电流 I 1、I 2、I 3。
5VA5VB5VCI 1I 2I 3图题 1-1解 I 1 6A , I 2 3A ,I 3 6A1-5在图题 1-5 所示电路中,求电流I 和电压 U AB 。
解I 4 1 2 1A ,U AB 3 10 2 4 4 39V 1-6在图题 1-6 所示电路中,求电压U 。
30V5U15V2AI 150V24 V图题 1-6图题 1-7解503052U ,即有 U 30V1-8 在图题 1-8 所示电路中,求各元件的功率。
3解电阻功率: P 322 3 12W , 2 AP 242 / 2 8 W电流源功率: P 2 A2(10 46) 0 ,2P1 A4 1 4 W10V电压源功率: P 10V10 2 20 W ,P4V4(12 2) 4 W图题 1-82-7 电路如图题 2-7 所示。
求电路中的未知量。
解U S2 6 12 VI 0124 AI 22AI 293I 3 P 3 /U S 12/12 1A USR eq69I 02 4/3 113/3A专业知识整理分享图题 2-7I 23 4V1AI 3 R 3P 3 12WWORD 格式可编辑R 312 121R eqU S12 36I 013/ 3 132-9 电路如图题 2-9 所示。
求电路中的电流I 1。
解 从图中可知, 2与 3 并联,12由分流公式,得I 2 3 5I 13I 1I 3 I 251VI 15I 131I 31 A1所以,有图题 2-9I 1 I 2 I 3 3I 11解得 I 10.5 A2-8 电路如图题 2-8 所示。
I 13I 2 ,求电路中的电阻 R 。
解KCL :I 1I 2 60I 1 2.2kI 13I 260mA解得 I 1 45mA, I 215 mA.I 2RR 为2.245R156.6 k图题 2-8解 (a)由于有短路线,R AB 6 , (b) 等效电阻为R AB1// 1 (1 1// 1) // 10.51.5 1.12.52-12 电路如图题2-12 所示。
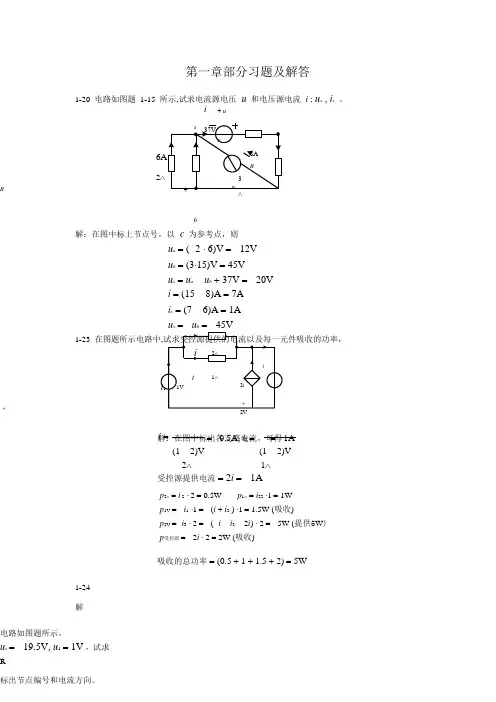
i = = 0.5A, i 2 = =1A 第一章部分习题及解答1-20 电路如图题 1-15 所示,试求电流源电压 u 和电压源电流 i ; u x , i x 。
i+ u2Rb解:在图中标上节点号,以 c 为参考点,则u a = ( 2 ⋅ 6)V = 12V u b = (3⋅15)V = 45V u x = u a u b + 37V = 20V i = (15 8)A = 7A i x = (7 6)A = 1A x b 1-23+解:在图中标出各支路电流,可得(1 2)V (1 2)V 2∧ 1∧受控源提供电流 = 2i = 1Ap 2∧ = i 2 ⋅ 2 = 0.5Wp 1∧ = i 22 ⋅1 = 1Wp 1V = i 1 ⋅1 = (i + i 2 ) ⋅1 = 1.5W (吸收)p 2V = i 3 ⋅ 2 = ( i i 2 2i ) ⋅ 2 = 5W (提供5W ) p 受控源 = 2i ⋅ 2 = 2W (吸收)吸收的总功率 = (0.5 + 1 + 1.5 + 2) = 5W1-24 解电路如图题所示,u s = 19.5V, u 1 = 1V ,试求R标出节点编号和电流方向。
ai +3∧u∧b+ui2∧4∧i+10ucRiiei1 =u11= 1A, u bc = u1 10u1 = 9Vu bc2u ab = i s ⋅ 3 = 10.5Vu ce = u cb + u ba + u s = (9 + 10.5 19.5) = 0V为确定R,需计算i4,u ce = u cd + u de = 0 ® u de = u cd = 10u1 = 10V故1-33 试用支路电流法求解图题所示电路中的支路电流i1, i2 , i3。
a 1∧ci+6Vb解求解三个未知量需要三个独立方程。
由KCL可得其中之一,即i1 + i2 + i3 = 5对不含电流源的两个网孔,列写KVL方程,得网孔badb网孔bdacb2i1 3i2 + 8 = 08 + 3i2 i3 + 6 = 0i 2 = = 4.5A, i s = i 1 + i 2 = 3.5Ai 3 = = 2.5A, i 4 = i s i 3 = ( 3.5 + 2.5)A = 1A整理得: ♦ 2i 1 2 = 8+ 3i ® ♦i 2 = 2A♥♥♣i 1 + i 2 + i 3 = 5 ♣i 1 = 1A ♠ ♠♠3i 2 i 3 = 2 ♠i 3 = 4A♦ i1 + 8i2 3i3 = 9 ® ♦i2 = 1A♥i3 = 1A® ♦♠(R +R)i M2 R1i M 1 R2i M 3 =u ♠♠♠==0♣i M 1 = 24 u® ♦(3 + 4)i M 3 = u ® ♦ ♥i M 3 i M 1 = 8♥ 第二章部分习题及解答2-1试用网孔电流法求图题所示电路中的电流i和电压u ab。
第一章习题1.1 题1.1图示一段电路N ,电流、电压参考方向如图所标。
(1) 若1t t =时1()1i t A =,1()3u t V =,求1t t =时N 吸收的功率1()N P t 。
(2) 若2t t =时2()1i t A =-,2()4u t V =,求2t t =时N()P t 解:(1) 111()()()313N P t ut i t W ==⨯= (2) 222()()()414N P t u t i t W ==⨯-=-1.2 题1.2图示一段直流电路N ,电流参考方向如图中所示,电压表内阻对测试电路的影响忽略不计,已知直流电压表读数为5V ,电流I 。
解: 1025P I A V -===-1.3 题1.3图示一个3A 的理想电流源与不同的外电路相接,求3A 电流源三种情况下供出的功率。
解:(a) 223218s P I R W ==⨯= 电流源输出功率 (b) 3515s P I V W ==⨯= 电流源输出功率(c) 31030s P I V W ==⨯-=- 电流源吸收功率1.4 题1.4图示某电路的部分电路,各已知的电流及元件值已标出在图中,求I 、s U 、R 。
解:流过3Ω电阻的电流为 12A+6A=18A 流过12Ω电阻的电流为 18A-15A=3A 流过电阻R 的电流为 3A-12A-5A=-14A 可得: I=-14A+15A=1A 18331290S U V =⨯+⨯= 1511231.514R ⨯-⨯==Ω-1.5 题1.5图示电路,已知U=28V ,求电阻R 。
解:根据电源等效,从电阻R 两端 可等效为如下图等效电路。
有: '41515442I A =⨯=+ '448R =Ω+Ω=Ω可得: '287152828U R U I R ===Ω--1.6 求题1.6图示各电路的开路电压。
解:(a) 2010530OC U V A V =-⨯Ω=-(b) 开路时,流过8Ω电阻的电流为 931189A ⨯=+ 流过6Ω电阻的电流为 1832189A ⨯=+可得: 26184OC U V =⨯-⨯=(c) 开路时,8Ω电阻的电压为 8208128V ⨯=+ 2Ω电阻的电压为 5210A V ⨯Ω= 可得: 82100OC U V V V V =+-=1.7 求题1.7图示各电路的电流解:(a) 6242I A +== (b) 201610221I A --==-+(c) 将电压源等效为电流源,如右图示 显然 0I =(d) 电压源供出的总电流为: 2121313//612//6124I A ===++++根据分流关系,流过3Ω电阻的电流为 63236A ⨯=+流过12Ω电阻的电流为 631126A ⨯=+可得: 211I A A A =-=1.8求题1.8图示各电路的电压U 。
习题和习题答案第 4 章必做习题习题 4-1 电路如图题 4.1 所示,求 6 Ω电阻吸收的功率。
习题 4-2 电路如图题 4.2 所示,试用叠加定理求电流 I 。
习题 4-3 电路如图题 4.3 所示,用戴维南定理计算 5 Ω电阻吸收的功率。
习题 4-4 电路如图题 4.4 所示,求 a 、 b 两端的诺顿等效电路。
习题 4-5 电路如图题 4.5 所示,用戴维南定理求电流 I 。
习题 4-6 电路如图题 4.6 所示,试问电阻 R 为何值时获得最大功率?并求最大功率。
第 4 章选做习题选做题 4-1 电路如图题 4.1 所示, N 是线性电阻网络,三个独立源 uS1 、uS2 和 iS 同时对 N 激励时,测得电流 i= 12A ;若将电压源 uS2 短路时,测得电流 i= 20A ;若将电压源 uS1 短路时,测得电流 i= - 5A 。
试问:将电流源 iS 和电压源 uS2 同时反向,而电压源 uS1 保持不变,电流 i 为多少?选做题 4-2 图题 4.2 所示电路中,已知 Uab=0 ,试用替代定理求电阻 R 。
选做题 4-3 电路如图题 4.3 所示,求 a 、 b 两端的戴维南等效电路。
选做题 4-4 图题 4.4 所示电路中, RL 可调,问 RL 为何值时获得最大功率?最大功率是多少?选做题 4-5 图题 4.17 所示电路中, Ns 是线性含源二端网络,电流表 A 和电压表 V 均是理想的,当开关 S 处于位置 1 时,电流表的读数为 2A ,当开关S 处于位置 2 时,电压表的读数为 4V ,求开关 S 处于位置 3 时, 5 Ω电阻吸收的功率。
选做题 4-6 求图题 4.6 所示电路中,电阻 R 获得最大功率时的电流 I 。
第 4 章必做习题精解习题 4-1解:为了求6 Ω电阻吸收的功率,就要先求出流过 6 Ω电阻的电流。
下面,用叠加定理计算电流 I 。
图题 4.1 电路中有两个独立源共同激励。
电路分析第五版答案第一章:基本概念和电路定律练习题答案a.看图1.1.CircuitCircuitb.从图中可以看出,电流I分为两个路径,通过电阻R1和R2。
根据欧姆定律,我们可以计算出电流I的值。
从电源V1开始,沿着电流的流向,电流经过电阻R1,其电压降为V1 - I R1。
然后经过电阻R2,其电压降为(V1 - I R1) - I * R2。
根据基尔霍夫电压定律,这个电压降等于电源的电压V1。
所以我们可以得到方程(V1 - I*R1) - I * R2 = V1。
通过解这个方程,我们可以计算出电流I的值。
a.如果电流经过电阻R1和电流源I1,那么根据欧姆定律,我们可以得到电流I1的值为I1 = V1 / R1。
b.如果电流经过电流源I2,则根据欧姆定律,我们可以得到电流I2的值为I2 = V2 / R2。
c.根据基尔霍夫电流定律,两个电流源的总和等于流入节点的电流总和。
所以我们可以得到I1 + I2 = I。
综上所述,我们得到了电路中的电流和电阻之间的关系。
第二章:电路简化技术练习题答案a.直接串联与并联等效电阻的计算公式为:–直接串联:R = R1 + R2 + R3 + ...–直接并联:1 / R = 1 / R1 + 1 / R2 + 1 / R3 + ...b.根据以上公式,我们可以计算出串联和并联电路的等效电阻。
a.并联电路等效电阻的计算公式为:1 / R = 1/ R1 + 1 / R2。
b.代入R1=4欧姆和R2=5欧姆的值,我们可以计算得到1 / R = 1 / 4 + 1 / 5。
进一步计算可得1 / R = 0.45。
最后,通过倒数运算可以得到R= 2.22欧姆。
所以,电路中的等效电阻为2.22欧姆。
实验题答案a.看图2.1.Simplified CircuitSimplified Circuitb.根据电路简化技术,我们可以将电感L1和L2合并,并求得等效电感L。
通过串联和并联电感的公式,我们可以得到等效电感的计算公式:L = L1 + L2。
电路分析基础练习题复刻回忆M 在图题M所示电路中。
元件A吸收功率30W■元件B吸收功率15W.元件C产生功率30W,分别求出三个元件中得电流 / I、/ 2 * ! 3。
4图题1-8所示电路中,求元件得功率。
电阻功率:W,W2-12电路如图题2・12所示。
求电路AB间得等效电阻。
1-51-6AAAA.VI】,求电莎O图题M_ I U在图题1-6所示电路中,求电压U。
•即苗图题,①1*11-8解电流源功率:,W电圧源功率:W.W电路如图题2・7所示。
求电路中得未知量。
()©2-7解AAA图题1・82-9解由分流公式,得电路如图题2・9所示。
求电路彳从图中可知,20匂3G并联,所以,有解得A2-8解电路如图题2・8所示。
已知,求电路中得电阻。
解得mA. mA、R为kn解(a)由于有短路线,,(b)等效电阻为图题2用R 孔电流法求如图题4-3所示电路中得血)显然,有一个超网孔,应用KVL 即 电流源•与网孔电流得关系 解得:A,A 电路中齐元件得功率为W.W.W.W显然,功率平衡。
电路中得损耗功率为740W 。
4- 10用节点电压法求如图题4-10所示电路中得电压。
解只需列两个节点方程解得yv所以4- 13 与闭合时得电压。
解由弥尔曼定理求解 开关S 打开时:V开关S 闭合时(a)3-4 (a ) (b )用电源变换得方法求如图题3-4所示电路中得电流人图題2-12 电路通过电源等效变换如图题解(a )、(b )、(0、型晦。
所毕电洱y 求得最简 f()V图题貳)3-6求如IM 题3・6T T 』 解V•专简单;KV 导 3-8 解 或 由 KCIp 联立解得Aa 球 (设电I寻电压。
井作出可以 F 表得卩fe 电I?平衡电桥,h4-2用艮图題解34b )图题4・2所示电K 图题解34c} 解先将电淤源模型戏唤成电压源模型,设网孔电流如I解得: AA A 所以 4-3解 V电路如图题4-13所示,求电路中开关S 打开F 示电路1电流劲电流表Q路T(d)图趙解34r4 图题解4{图题3・14•丄・5- 4用叠加泄理求如图题54所示电路中得电压以 解应用叠加出理可求得 10V 电压源单独作用时:5- 8图题5・8所示无源网络N 外接Us=2V ・ 时侧响应/为多少?解根据叠加定理:/=5/2X4+5/2X2=15A5-10求如图题5・10所示电路得戴维南等效电路。