当前位置：文档之家 › 《电路分析基础》典型例题.pptx

《电路分析基础》典型例题.pptx

  • 格式：pptx
  • 大小：97.52 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

电路分析基础ppt课件

电路分析基础ppt课件
详细描述
欧姆定律是电路分析中最基本的定律 之一，它指出在纯电阻电路中，电压 、电流和电阻之间的关系为 V=IR，其 中 V 是电压，I 是电流，R 布问题的 定律
VS
详细描述
基尔霍夫定律包括两个部分：基尔霍夫电 流定律（KCL）和基尔霍夫电压定律（ KVL）。基尔霍夫电流定律指出，对于电 路中的任何节点，流入节点的电流之和等 于流出节点的电流之和；基尔霍夫电压定 律指出，对于电路中的任何闭合回路，沿 回路绕行一圈，各段电压的代数和等于零 。
电路分析基础PPT 课件
目 录
• 电路分析基础概述 • 电路元件和电路模型 • 电路分析的基本定律和方法 • 交流电路分析 • 动态电路分析 • 电路分析的应用实例
01
电路分析基础概述
电路分析的定义
电路分析
电路分析的方法
通过数学模型和物理定律，研究电路 中电压、电流和功率等参数的分布和 变化规律的科学。
时不变假设
电路中的元件参数不随时间变化， 即电路的工作状态只与输入信号的 幅度和相位有关，而与时间无关。
02
电路元件和电路模型
电阻元件
总结词
表示电路对电流的阻力，是电路中最基本的元件之一。
详细描述
电阻元件是表示电路对电流的阻力的一种元件，其大小与材料的电导率、长度 和截面积等因素有关。在电路分析中，电阻元件主要用于限制电流，产生电压 降落和消耗电能。
二阶动态电路的分析
总结词
二阶RLC电路的分析
详细描述
二阶RLC电路是指由一个电阻R、一个电感L和一个电容C 组成的电路，其动态行为由二阶微分方程描述。通过求解 该微分方程，可以得到电路中电压和电流的变化规律。
总结词
二阶动态电路的响应

电路分析典型例题-PPT课件

电路分析典型例题-PPT课件

i3
i1=0.5A
b
d
i2=1.5A i3=0.5A
ucd=4 V i=2A
u= ucd +3i = 10V
R u 5 i
故单口网络的最简形式如图所示。
第三章 线性电路分析方法
1、独立的KCL、KVL方程数；支路电流法计算步骤；
2、网孔电流法： 推广：对于具有 l=b-(n-1) 个回路的电路，有:
4、节点、支路、回路、网孔定义，KCL、KVL 内容、数学表达式，扩展应用。
课堂练习：P26 1-5
课堂练习：P27 1-8
I268A
U281V 6
P Is61 69W 6
发出功率，为电源
P 281 612 W8
吸收功率，为负载
I
P 外21 63W 2
发出功率，为电源
例: 如图电路，已知IS1=1.5A,
R2=R3=8, =4 , 求I2和I3？
I S1
解：由电压源和电流源等效替换，把支 路2的受控电压源转换为受控电流源。
r I3 I3
I2
R3
R2
得等效电流源为I3/R2，电路如图
由分流公式可得
I3 R2 (IS1I3)
R2R3 R2
IS1
R2
I3
r I3
R2 R3
I2
代入数据有 I3 = 0.5（1.5＋0.5I3）
I3 = 1 A
I2 = IS1－I3 = 0.5 A
IS1
I3
R2
r I3
R2 R3
I2
输入电阻
1. 定义
无 源
i
+ u
-
输入电阻
R in

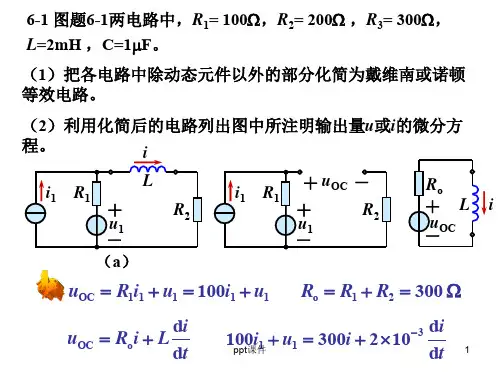
电路分析基础第6章习题答案 ppt课件

电路分析基础第6章习题答案 ppt课件

7
dt
6-4 图题6-4所示电路中，各电源均在 t =0时开始作用于电路，
求 i (t)，已知电容电压初始值为零。
i(t)
i(t)
4k ＋
1V －
1mA
4k
＋
6k
＋
uOC
2F
1V－
－
1mA 6k
把除电容元件以外的电路进行戴维南变换
(1 4k

1 6k
)uOC

10 3

1 4k
uOC 3 V
＋
4
u
i1(t)
－
18
6-9 电路如图题6-8所示，电压源于 t =0 时开始作用于电路，试 求i (t)，t≥0。
－10i1(t)＋
4A 4 2H i1(t) i(t)
14
＋
2H
－56V i(t)
时间常数为： 2 1 s
14 7
稳态时 i() 56 4 A 14
t
i(t) i()(1 e ) 4(1 e 7t ) V t≥0
4

103

ppt课件
(0.5

0.75e
208.3t
)
mA
t≥0
9
6-5 电路如图题6-5所示，开关在 t =0时闭合，求t=15s时ua及
各支路电流。 设电容的初始储能为零
＋200V 60k 40k
6k 1000pF
＋ ua uC －
－300V
时间常数为： RoC (60k // 40k 6k)109 3105 s
1.5 1.25 1.2 16
6-8 电路如图题6-7所示，电压源于 t =0 时开始作用于电路，试

《电路分析基础》课件

《电路分析基础》课件

电路基础知识
1 电流
电流是电子在电路中差。它的单位是伏特（V）。
3 电阻
电阻是电流受到阻碍的程度。它的单位是欧姆（Ω）。
电路元件和符号
电阻器
电容器
电阻器用于限制电流流过的路径， 以控制电路中的电阻。
电容器能够储存电荷，并在需要 时释放电荷。
《电路分析基础》PPT课 件
这个PPT课件将介绍电路分析的基础知识，包括电路元件和符号、欧姆定律与 基尔霍夫定律、串并联电路计算、交流电路分析以及电感和电容的应用。
课程介绍
本课程旨在帮助学生掌握电路分析的基本概念和技能，了解电路元件以及符 号表示方法。通过实例演示和练习，学生将能够应用欧姆定律和基尔霍夫定 律解决简单的电路问题。
多个电阻平行连接，总电流等于各个电阻的电流 和。
交流电路分析
1
正弦波形
交流电路中最常见的波形，可通过正弦函数表示。
2
复数形式
使用复数形式来描述交流电路的电压和电流，以便进行计算。
3
复阻抗
交流电路中的电阻用复数表示，称为阻抗。
电感和电容的应用
电感和电容在电路中有许多重要应用，包括滤波器、振荡器、调谐电路等。它们是实现不同功能的关键元件。
电感器
电感器存储电流的磁场能量，并 在需要时释放它。
欧姆定律与基尔霍夫定律
欧姆定律
欧姆定律描述了电流、电压和电阻之间的关系，即 V = IR。
基尔霍夫定律
基尔霍夫定律是应用于复杂电路的两个定律：电流 守恒定律和电压守恒定律。
串、并联电路计算
串联电路 并联电路
多个电阻依次连接在一起，电流在电阻间是相同 的。

《电路分析基础》典型例题

《电路分析基础》典型例题

例2-15 用网孔法求图2-24所示电路的网孔电流，已知1=μ，1=α。

解：标出网孔电流及序号，网孔1和2的KVL 方程分别为m1m2m362216I I I --=m1m2m31262I I I U μ-+-=-对网孔3，满足m33I I α=补充两个受控源的控制量与网孔电流关系方程1m12U I =；3m1m2I I I =-将1=μ，1=α代入，联立求解得 m1m2m34A 1A 3A I I I ===，，。

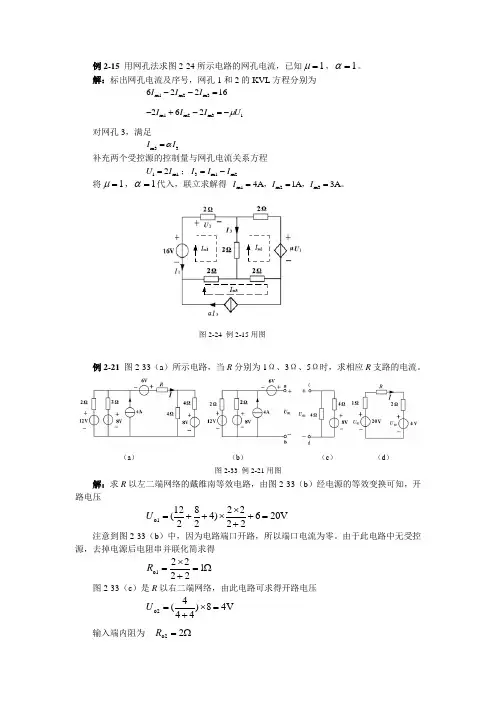
例2-21 图2-33（a ）所示电路，当R 分别为1Ω、3Ω、5Ω时，求相应R 支路的电流。

（a ） （b ） （c ） （d ）图2-33 例2-21用图解：求R 以左二端网络的戴维南等效电路，由图2-33（b ）经电源的等效变换可知，开路电压V2062222)428212(o1=++⨯⨯++=U注意到图2-33（b ）中，因为电路端口开路，所以端口电流为零。

由于此电路中无受控源，去掉电源后电阻串并联化简求得Ω=+⨯=12222o1R 图2-33（c ）是R 以右二端网络，由此电路可求得开路电压V 48)444(o2=⨯+=U输入端内阻为 Ω=2o2R图2-24 例2-15用图再将上述两戴维南等效电路与R 相接得图2-33（d ）所示电路，由此，可求得R ＝1Ω时， A 4211420=++-=IR ＝3Ω时， A 67.2321420=++-=IR ＝5Ω时， 2042A 125I -==++例3-10 在图3-26所示的电路中，电容原先未储能，已知U S = 12V ，R 1 = 1k Ω，R 2 = 2k Ω，C =10μF ，t = 0时开关S 闭合，试用三要素法求开关合上后电容的电压u C 、电流i C 、以及u 2、i 1的变化规律。

解：求初始值C C (0)(0)0u u +-==S1C 1(0)(0)12mA U i i R ++=== 求稳态值2C S 12R ()8V u U R R ∞==+ C ()0A i ∞=S112()4mA U i R R ∞==+求时间常数12121s 150R R C R R τ⨯==+写成响应表达式t150t τC C C C ()[(0)()]8(1)V u u u u e e --+=∞+-∞=-t 150t τC C C C ()[(0)()]12mA i i i i ee --+=∞+-∞=t -150t τ1111()[(0)()](48)mA i i i i e e -+=∞+-∞=+例3-11在图3-27所示的电路中，开关S 长时间处于“1”端，在t =0时将开关打向“2”端。

电路分析基础试卷含答案.pptx

电路分析基础试卷含答案.pptx

1） uL (0 )e2t 2） uL (0 )e0.5t 3） uL (0 )(1 e2t )
7、4 电阻、1H 电感和 1F 电容串联二阶电路的零输入响应属于 1）过阻尼 2）欠阻尼 3）临界阻尼
情况。
8、RLC 并联正弦电流电路中， IR 3A, IL 1A, IC 5A 则总电流为
16、图示单口网络的功率因素为（） 1）0.8 2）0.707 3）-0.6 4）0.6
17、图示电路中电阻 R 吸收的平均功率 P 等于（）
1）12.5W 2）16W 3）32W 4）25W
18、图示电路中负载获得的最大平均功率等于（） 1）2.5W 2）5W 3）10W 4）20W
19、图示单口网络的等效电感为（） 1）1H
2、由叠加定理求得 u1 (4 2 2) 8V,u2 (4 4 2) 2V 。
3、 uoc
3V , R0
4, p max
32 W 44
0.5625W
4、 uc (0 ) 6V,uc () 6V, 2s
uc (t) (6 12e0.5t )V (t 0)
6
学海无 涯
5、 I IL IC
_
_
13、图示正弦电流电路中电压u(t) 的初相等于（） 1） 36.9 2） 36.9
2
us (t) cos(2t)V
3
+ +
us
u
_
_
us (t) 5cos(2t)V
学海无 涯
3） 53.1
4） 53.1
14、图示单口网络相量模型的等效阻抗等于（） 1）(3+j4) 2）(0.33-j0.25) 3）(1.92+j1.44) 4）(0.12+j0.16) 15、图示单口网络相量模型的等效导纳等于（） 1）(0.5+j0.5) S 2）(1+j1) S 3）(1-j1) S 4）(0.5-j0.5) S

电路分析基础完整ppt课件

电路分析基础完整ppt课件

可否短路？
恒压源特性中不变的是：__ __U_S________
恒压源特性中变化的是：_____I________
___外__电__路__的__改__变____ 会引起 I 的变化。
I 的变化可能是 _大__小____ 的变化，
或者是__方__向___ 的变化。
22.04.2020
.
24
电工基础教学部
电路的基本分析方法。
22.04.2020
.
电工基础教学部
4
目录
电工电子技术
1.1 电路元件
1.1.1 电路及电路模型
电路——电流流通的路径。
1.电路的组成和作用
电路是由若干电路元件或设备组成的，能够传输能 量、转换能量；能够采集电信号、传递和处理电信号 的有机整体。
①电路的组成：
电源 信号源
中间环节
目录
电工电子技术
②理想电流源（恒流源): RO= 时的电流源.
Ia
Uab
外
Is
U RL
特
I性
b
o
IS
特点：（1）输出电流 I 不变，即 I IS （2）输出电压U由外电路决定。
22.04.2020
.
电工基础教学部
25
目录
电工电子技术
（3）恒流源的电流 IS为 零时，恒流源视为开路。
IS=0
（4）与恒流源串联的元件对外电路而言为可视为短路。
E
+ _
R2
Is
a
R1 b
Is
a R1
b
例 设: IS=1 A
则: R=1 时， U =1 V Is R=10 时， U =10 V
I UR

《电路分析基础》PPT课件..课件

《电路分析基础》PPT课件..课件



基尔霍夫电压方程也叫回路电压方程（KCL方程）
精品
基尔霍夫电压定律（KVL）

基尔霍夫电压定律的另一种描述：集总参数电
路中，沿任意闭合回路绕行一周，电压降的代数 和=电压升的代数和。

基尔霍夫电压定律是能量守恒的结果，体现了
电压与路径无关这一性质，是任一回路内电压必 须服从的约束关系。
精品
KVL示例

电阻消耗的瞬时功率
参考方向一致时 参考方向不一致时

电阻消耗的能量
精品
1.5 独立电源

术语

电路中的电源：
独立电源：就是电压源的电压或电流源的电流不受外电 路的控制而独立存在的电源。 受控电源：是指电压源的电压和电流源的电流，是受电 路中其它部分的电流或电压控制的电源。 电压源和电流源
精品
电压源
精品
支路、节点、回路、网孔
支路： 1、2、3、4、5、6、7 节点： ①、②、③、④、⑤ 简单节点： ④
回路： ①-②-③-④-① ①-②-⑤-① ①-②-⑤-③-④-①等等。 网孔： ①-②-③-④-① ①-②-⑤-① ②-③-⑤-② 思考:①-②-③-⑤-①是网孔吗? 网孔一定是回路，但回路不一定是网孔。精品

电路的组成(component)


激励与响应
精品
1.1电路和电路模型

电路的作用：能量和信息两大领域

1.电力系统：实现电能的传输和转换。 能量是主要的着眼点。涉及大规模电能的产生、 传输和转换(为其他形式的能量)，构成现代工业生产、 家庭生活电气化等方面的基础。
精品
1.1电路和电路模型
电路分析基础
精品

电路分析基础教学PPT

电路分析基础教学PPT

课间休息
1-3 支路电流法
支路电流法是以基尔霍夫定律为基础的、用 于分析复杂电路的一种有效方法。
❖ 列方程时，必须先在电路图标出电流的参考方向， 这个方向是任意的。
❖ 求解过程 (1) 应用KCL，列出结点电流方程,n个结点列 n-1个方程； (2) 应用KVL，列出回路电压方程。
❖ 注意 在列回路电压方程时，选用单孔回路，这样才能
供给外电路的端电压保持为
电动势E不变，该电源称为
理想电压源。
理想电压源提供的电压没有 内部损耗。
R0I
U
I
1-1 电路的基本概念
2、开路 开路即是将电路断开。 电路电流为0，I=0 负载电压为0，U=0
S I=0
R0
U0
E
RU
电源端电压依然存在，并且U=E-R0I=E，该
电压称为开路电压，用U0表示，即U0=E。
第1章 电路分析基础
概述 本章所讲述的电路分析知识对后续直
流电路、交流电路、电机电路和电子电路 都具有实用意义，请务必充分重视。
第1章 电路分析基础
1-1 电路的基本概念
一、电路的组成
电路是电流的通路。是为了某种需要由某些电 工设备或元件按一定方式组合起来的。 根据电流性质分类
➢ 直流电路 ➢ 交流电路
位高10V。
b-
❖ 电位是一个相对概念，单纯的电位没有意义。 必须选取一个参考点，才能谈及电位。
❖参考点可任意选取，被选取的参考点是被作为 一个标准，这个参考点的电位称为参考电位，通 常设为零。
❖参考点在电路图中标以“接地”符号，但并不 是真正意义上的接地。
作业： P10：思考题1-2-2、1-2-3
1-1 电路的基本概念

电路分析基础ppt课件

电路分析基础ppt课件
叠加定理
叠加定理是指在分析暂态电路时，可以将激励（即输入）信号分解为多个正弦波信号，然后分别求解 每个正弦波信号引起的响应（即输出），最后将各个响应叠加起来得到总的响应。
综合应用案例分析
07
综合应用案例一：一个实际电路的分析
总结词
这是一个实际电路，我们需要运用所学 的电路分析基础来理解和分析它的工作 原理。
的性能是否符合要求。
THANKS.
VS
详细描述
首先，我们可以根据电路图识别出各个元 器件及其作用，然后根据欧姆定律、基尔 霍夫定律等基本原理来计算电流、电压等 参数，从而理解电路的工作过程。
综合应用案例二：一个复杂电路的分析
总结词
这是一个复杂电路，我们需要运用所学的电 路分析基础来理解和分析它的工作原理。
详细描述
对于复杂电路，我们需要采用一些高级的分 析方法，如支路电流法、节点电压法等，来 计算各个支路上的电流、各个节点的电压等 参数，从而理解电路的工作过程。
RL电路
在RL电路中，电感L和电阻R串联，当开关从闭合状态变为断开状态时，电感L会通过电阻R放电，电流i(t)可以用 以下公式表示：i(t)=I_0(1-exp(-t/τ))，其中I_0为初始电流，τ为时间常数。
暂态电路的基本分析方法
节点电压法
在暂态电路中，节点电压是指在该节点处的电压降。节点电压法是通过求解节点电压来分析暂态电路 的一种方法。
电路分析基础ppt课件
目 录
• 电路分析概述 • 电阻电路分析 • 电容电路分析 • 电感电路分析 • 交流电路分析 • 暂态电路分析 • 综合应用案例分析
电路分析概述
01
电路分析的基本概念
电路分析的定义
电路分析是对电路进行建模、分 析和计算的过程，以了解电路的 性能和优化其设计。

电路分析基础例题集(第1-5章)讲解

电路分析基础例题集(第1-5章)讲解
例1.8如图1.8所示电路，已知电阻 消耗的功率为 ，求电阻 的大小。
图1.8
解题思路：由 及 可解出用电阻 表示的电流 ，再利用电阻 消耗的功率为 的条件可求出电阻 的值。
，所以
整理得
解得
或
例1.9如图1.9（a）所示电路，已知 的功率为 ，求 、 和 的值。
所以
（b）图中的 、 为关联参考方向，故其功率为
所以
（c）图中的 、 为非关联参考方向，故其功率为
所以
例1.3如图1.3所示电路，已知 ，求 和 。
图1.
解题思路：可由电容的 求出电容电流，由欧姆定律求出电阻电流，然后由后面将要介绍的基尔霍夫电流定律（ ）求出电感电流 ，再由电感的 求出电感电压，最后由基尔霍夫电压定律（ ）求出 。
解：标注电流 和 如图1.10（b）所示。由已知条件可得
，
故
例1.11如图1.11（a）所示电路，求电阻 。
图1.
解题思路：先用 求出通过上边 电阻的电流，然后用 和 求出图1.11（b）所示 和 ，最后用欧姆定律求出电阻 。
解：标注电流和电压如图1.11（b）所示。在图1.11（b）的上边左网孔应用 可得
，
例3.4如图3.4所示电路，用网孔电流法求电流 。
解题思路：先确定每个网孔电流及其绕行方向，然后在列写其网孔电流方程并求解。图3.4中的网孔电流 为已知量，该网孔不需要列写网孔电流方程（就是要写也必须按替代定理的思路来处理，详见例3.5）。
图3.
解：设网孔电流及其绕行方向如图3.4所示，其网孔电流方程为
所以电压源的功率为
（发出）
电流源的功率为
（吸收）
电阻的功率为
（吸收）
电路发出的功率为 ，吸收的功率为 ， ，所以电路的功率是平衡的。事实上，所有电路的功率都是平衡的，否则就会违反能量守恒原理。

§12-2电路分析基础例题

§12-2电路分析基础例题

1 2
I2
10
1 2
I2
I2
5
j
1 2
10
5
j
Z
1210 1210
j5 j5
1210 j5 1210 j5
1 I1 U 1
1
0.2F 2
10
I2
10 U 2
0.2F
2
例题4 求如图所示二端口网络的Y参数。
解： 端口 22' 短路时：
Y11 Y21
I1 U 1
UI21
U 2 0 U 2 0
1 I1
11' 端口开路：
U1
Z12
U 1 I2
I1 0
R1
R1
R3 R2 I2
R3
I2
1
R1 R3 R1 R2
R3
Z 22
U 2 I2
I1 0
R3
/
/( R1
R2 )
R3 ( R1 R2 ) R1 R2 R3
R2 R1 R3
I2 2
U 2
2
例题2 求如图所示二端口网络的Z参数。
解：
22' 端口开路：
Z11
U 1 I1
I2 0
j10
Z 21
U 2 I1
I2 0
j10
11' 端口开路：
1 I1
U1
4I2
1
Z12
U 1 I2
I1 0
4 I2
j10I2 I2
4
j10
Z 22
U 2 I2
I1 0
3 j10
3 I2 2
j10
U
2
2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

解：已知线电压为U L 380V，则相电压为U源自P1U 3
L220V
，
因此线电流
IL
UP Z
负载的阻抗角为
220 44A 42 32
P
arctan
3 36.9 4
因此三相负载总的有功、无功和视在功率分别为
P 3ULIL cosP 3 380 44 cos36.9 23.16kW Q 3ULILsinP 3 380 44 sin 36.9 17.38kVar
cos cos[20o (33.1o )] 0.6
例 4-22 某个 RLC 串联谐振电路中 R=100Ω，C=150pF，L=250μH，试求该电路发生谐 振的频率。若电源频率刚好等于谐振频率，电源电压 U=50V，求电路中的电流、电容电压、 电路的品质因数。
解：
0
1
1
rad/s 5.16106rad/s
C
C
C
C
t
uR u (R) [u (R0 ) u (R)]e τ 15e V 0.5t
例 4-20RLC 串联电路，已知 R=30Ω、L=254mH、C=80μF，u 220 2 sin(314t 20o )V ，求： 电路有功功率、无功功率、视在功率、功率因数。
解：
•
U 22020o V
Z R j(XL XC ) 30 j(79.8-39.8)
(30 j40) 5053.1o
•
•
I
U
22020o
4.4
33.1oA
Z 50 53o
S UI 220 4.4 968VA
P UIcos 968cos[20o (33.1o)] 581.2W
Q UIsin 968sin[20o (33.1o )] 774.1Var
图 3-27 例 3-11 图 2
学海无 涯
解：求初始值
uC(0
)
u
(C0
)
24 3
5 5
15V
求稳态值
uR (0 ) uC(0 ) 30 15V
uC() 30V
uR () 0V
求时间常数
RC 4 103 500 106 s 2s
写成响应表达式
t
u u () [u (0 ) u ()]e τ (30 15e-0.5t)V
LC 150 1012 250 106
3
学海无 涯
f0
0 2
5.16106 z 8.2 105z 2 3.14
I 0
U R
50 A 100
0.5A
1 L 5.16 250 1290 C
1
UC C I0 645V
Q L 12.9
R
例 5-5 对称星形连接的三相负载，每相阻抗为 Z (4 j3) ，三相电源线电压为 380V， 求三相负载的总功率。
1
学海无涯
再将上述两戴维南等效电路与 R 相接得图 2-33（d）所示电路，由此，可求得
R＝1Ω时， I 20 4 4A 11 2
R＝3Ω时， I 20 4 2.67A 1 2 3
R＝5Ω时， I 20 4 2A 1 25
例 3-10 在图 3-26 所示的电路中，电容原先未储能，已知 US=12V，R1=1kΩ，R2=2kΩ，C=10μF， t=0 时开关 S 闭合，试用三要素法求开关合上后电容的电压 uC、电流 iC、以及 u2、i1 的变化 规律。
将 1， 1 代入，联立求解得 Im1 4A，Im2 1A，Im3 3A。
图 2-24 例 2-15 用图
例 2-21 图 2-33（a）所示电路，当 R 分别为 1Ω、3Ω、5Ω时，求相应 R 支路的电流。
（a）（b）（c）（d）
图 2-33 例 2-21 用图
解：求 R 以左二端网络的戴维南等效电路，由图 2-33（b）经电源的等效变换可知，开 路电压
t
iC i (C) [i (C0 ) i (C )]e τ 12e 150t mA
i1
i 1()
[ i 1(0
)
i 1()]e
-t
τ
(4
8e
150t)mA
例 3-11 在图 3-27 所示的电路中，开关S 长时间处于“1”端，在 t=0 时将开关打向“2”端。
用三要素法求 t>0 时的 uC、uR。
U o1
12 (
2
8 2
4)
2 2 2 2
6
20V
注意到图 2-33（b）中，因为电路端口开路，所以端口电流为零。由于此电路中无受控
源，去掉电源后电阻串并联化简求得
Ro1
2 2
2 2
1
图 2-33（c）是 R 以右二端网络，由此电路可求得开路电压
U o2
( 4 )8 44
4V
输入端内阻为 Ro2 2
S 3ULIL 3 380 44 28.96kV A
4
解：求初始值
uC (0 ) uC (0 ) 0
i1(0 )
iC
(0 )
US R1
12mA
求稳态值
uC()
R R1
2
R
2
U
S
8V
iC() 0A
i1()
US R1 R2
4mA
求时间常数
R1 R2 C 1 s
R1 R2 150 写成响应表达式
图 3-26 例 3-10 图
t
uC u (C) [u (C0 ) u (C )]e τ 8(1 e 150t)V
学海无 涯
例 2-15 用网孔法求图 2-24 所示电路的网孔电流，已知 1， 1 。
解：标出网孔电流及序号，网孔 1 和 2 的 KVL 方程分别为 6Im1 2Im2 2Im3 16
2Im1 6Im2 2Im3 U1
对网孔 3，满足
Im3 I3
补充两个受控源的控制量与网孔电流关系方程 U1 2Im1 ； I3 Im1 Im2