下载文档原格式
摘要本文通过对数据建立数学建模竞赛的预测模型和定量评估模型，并对夏季运动会进行了评价。
通过历届夏季奥运会的运动员人数等相关数据，运用二次指数平滑预测法建立了人数预测的数学模型；另外，竞赛项目的普及程度、流行程度和财政收入情况，能够在一定程度上反映各竞赛项目的全球影响力水平，即采用数理统计法进行研究，选取此3项一级指标和14项二级指标进行统计学分析，对夏季奥运会竞赛项目的全球影响力进行综合评估、对比和档次的划分，并作合理化建议。
针对问题一，运用二次指数平滑预测法建立了预测函数：212121ˆ156093360T ya b T T +=+=+对函数进行合理的运算和证明，所得到的结果为18969人，误差预测结果为0.3178，说明模型的拟程度很好。
对于问题二，运用综合评价的思想，定义指标函数：12341nii PP P P P ==+++∑根据全球影响力总分的百分位数划分出4个档次，对各档次项目的全球影响力进行定量评估，并提出合理化建议。
关键字：二次指数平滑 数理统计法 定量分析 综合评价模型一、问题重述奥林匹克运动是人类社会的一个罕见的杰作，它将体育运动的多种功能发挥得淋漓尽致，影响力远远超出了体育的范畴。
请搜集参加历届夏季奥运会的运动员人数等数据，试着探讨以下问题：（1）建立数学模型，预测2012年第30届伦敦奥运会参赛运动员人数。
（2）定量评价夏季奥运会，并提出合理化建议。
二、问题分析本题目主要研究奥运会参赛运动员的人数，以及通过已有的数据对夏季奥运会竞赛项目全球影响力进行定量分析，进而对其影响力和发展前景提出合理化建议。
问题一：是建立模型预测2012年第30届伦敦奥运会参赛运动员人数，属于预测分析的问题，并通过简单的分析可知，每届参赛的数量呈明显上升趋势，所以该问题可采用时间序列预测中的二次指数平滑预测法建立模型，以参赛人数为研究对象，对数据整理后，运用二次多项式对数据进行拟合预测。
问题二：是对夏季奥运会进行定量评估，主要采用数理统计法进行研究，选取国际奥委会项目委员会上所作报告中的3项一级指标（竞赛项目普及度、流行度、财政收入)，14项二级指标作为各竞赛项目全球影响力评估分析的依据。
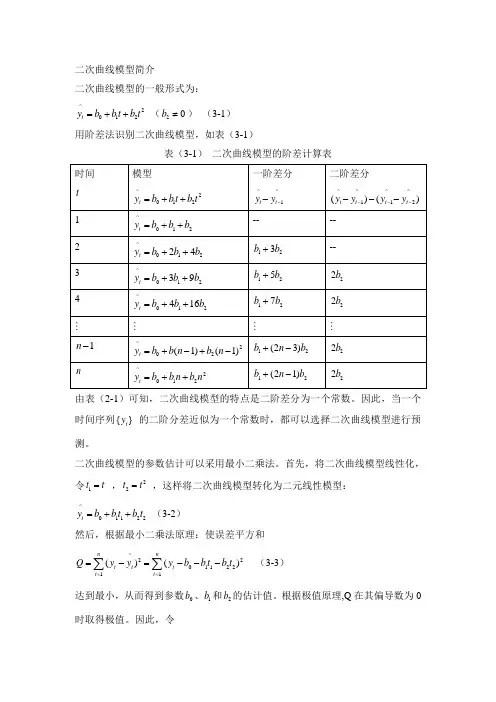
二次曲线模型简介二次曲线模型的一般形式为：^2012t y b b t b t =++ （20b ≠） （3-1）用阶差法识别二次曲线模型，如表（3-1）表（3-1） 二次曲线模型的阶差计算表由表（2-1）可知，二次曲线模型的特点是二阶差分为一个常数。
因此，当一个时间序列{}t y 的二阶分差近似为一个常数时，都可以选择二次曲线模型进行预测。
二次曲线模型的参数估计可以采用最小二乘法。
首先，将二次曲线模型线性化，令1t t = ，22t t = ，这样将二次曲线模型转化为二元线性模型：^01122t y b b t b t =++ （3-2）然后，根据最小二乘法原理：使误差平方和^220112211()()nnt t t t t Q y y y b b t b t ===-=---∑∑ （3-3）达到最小，从而得到参数0b 、1b 和2b 的估计值。
根据极值原理,Q 在其偏导数为0时取得极值。
因此，令01122001122110112222202()02()0t t t Qy b b t b t b Qy b b t b t t b Qy b b t b t t b ⎧∂=----=⎪∂⎪⎪∂=----=⎨∂⎪⎪∂=----=⎪∂⎩∑∑∑ （3-4） 整理后即的正规方程组：01122210111212220211222t t ty nb b t b t t y b t b t b t t t y bt b t t b t ⎧=++⎪=++⎨⎪=++⎩∑∑∑∑∑∑∑∑∑∑∑ （3-5）即：2012230122234012t t t y nb b t b t ty b t b t b t t y b t b t b t ⎧=++⎪=++⎨⎪=++⎩∑∑∑∑∑∑∑∑∑∑∑ （3-6）最后，求解三元一次线性方程组式（3-6），即可得到参数0b 、1b 和2b 的估计值，从而得到二次曲线模型。
三次指数平滑法简介2.1.1 指数平滑公式如果时间序列的变化呈现二次曲线趋势时，可用三次指数平滑法进行预测。
java⼆次指数平滑法预测未来的值指数平滑法是⼀种特殊的加权平均法，加权的特点是对离预测值较近的历史数据给予较⼤的权数，对离预测期较远的历史数据给予较⼩的权数，权数由近到远按指数规律递减，所以，这种预测⽅法被称为指数平滑法。
它可分为⼀次指数平滑法、⼆次指数平滑法及更⾼次指数平滑法。
⼀次指数平滑的局限性：像⼀次移动平均法⼀样，⼀次指数平滑法只适⽤于⽔平型历史数据的预测，⽽不适⽤于斜坡型线性趋势历史数据的预测。
⽽⼆次指数平滑法就是以斜坡型为模型来预测未来数据。
除了⼆次指数平滑法外，还有更⾼次的多次指数平滑法，由于它们在实际预测中并不常⽤，因此忽略。
所以就以⼆次指数平滑法为例： /*** ⼆次指数平滑法求预测值* @param list 基础数据集合* @param year 未来第⼏期* @param modulus 平滑系数* @return预测值*/private static Double getExpect(List<Double> list, int year, Double modulus ) {if (list.size() < 10 || modulus <= 0 || modulus >= 1) {return null;}Double modulusLeft = 1 - modulus;Double lastIndex = list.get(0);Double lastSecIndex = list.get(0);for (Double data :list) {lastIndex = modulus * data + modulusLeft * lastIndex;lastSecIndex = modulus * lastIndex + modulusLeft * lastSecIndex;}Double a = 2 * lastIndex - lastSecIndex;Double b = (modulus / modulusLeft) * (lastIndex - lastSecIndex);return a + b * year;}测试代码：public static void main(String[] args) {List<Double> list = new LinkedList<Double>();list.add(253993d);list.add(289665d);list.add(342785d);list.add(384763d);list.add(428964d);list.add(470614d);list.add(530217d);list.add(620206d);list.add(688212d);list.add(746422d);list.add(809592d);list.add(791376d);list.add(772682d);list.add(806048d);list.add(860855d);list.add(996633d);list.add(1092883d);list.add(1172596d);list.add(1245356d);list.add(1326094d);list.add(1378717d);list.add(1394413d);list.add(1478573d);list.add(1534122d);list.add(1608150d);Double value = getExpect(list, 1, 0.6);System.out.println(value);}。
二次指数平滑预测模型回归系数计算方法概述二次指数平滑预测模型是一种比较常用的时间序列预测模型，它用来对时间序列数据进行预测，其中回归系数是确定模型的关键参数，计算回归系数的方法是非常重要的，本文将探讨二次指数平滑预测模型回归系数计算方法。
一、原理二次指数平滑预测模型是一种比较常用的时间序列预测模型，它用来对时间序列数据进行预测，其中回归系数是确定模型的关键参数，计算回归系数的方法是非常重要的。
二次指数平滑预测模型的回归系数计算方法是：首先，计算最小二乘估计值，即：$$ \hat{\beta} = (X^T X)^{-1} X^T Y $$其中，$X$是自变量矩阵，$Y$是因变量向量，$\hat{\beta}$是回归系数估计值。
然后，计算二次指数平滑预测模型的回归系数，即：$$ \beta = \alpha \hat{\beta} + (1 - \alpha) \beta_{t-1} $$其中，$\alpha$是模型参数，$\beta_{t-1}$是上一时刻的回归系数。
二、实例下面以一个实例来说明二次指数平滑预测模型的回归系数计算方法。
假设有一个时间序列数据，其自变量矩阵为：$$ X = \left[ \begin{matrix} 1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_n \end{matrix} \right] $$而因变量向量为：$$ Y = \left[ \begin{matrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{matrix} \right]首先，计算最小二乘估计值，即：$$ \hat{\beta} = (X^T X)^{-1} X^T Y $$其中，$X^T X$为$3 \times 3$矩阵，$X^T Y$为$3 \times 1$矩阵，因此，$\hat{\beta}$为$3 \times 1$矩阵，其中有三个回归系数。
二次指数平滑法二次指数平滑法（Second exponential smoothing method）[编辑]什么是二次指数平滑法二次指数平滑法是对一次指数平滑值作再一次指数平滑的方法。
它不能单独地进行预测，必须与一次指数平滑法配合，建立预测的数学模型，然后运用数学模型确定预测值。
一次移动平均法的两个限制因素在线性二次移动平均法中也才存在，线性二次指数，平滑法只利用三个数据和一个α值就可进行计算；在大多数情况下，一般更喜欢用线性二次指数平滑法作为预测方法。
[编辑]二次指数平滑法的优点[1]二次指数平滑法实质上是将历史数据进行加权平均作为未来时刻的预测结果。
它具有计算简单、样本要求量较少、适应性较强、结果较稳定。
[编辑]二次指数平滑法的计算线性二次指数平滑法的公式为：(1)式中：分别为t期和t–1期的二次指数平滑值；a为平滑系数。
在和已知的条件下，二次指数平滑法的预测模型为：(2)(3)T为预测超前期数例5：某地1983年至1993年财政入的资料如下，试用指数平滑法求解趋势直线方程并预测1996年的财政收入。
计算过程及结果如下：由上表可知：；；；,a=0.9 则所求模型为:[编辑]二次指数平滑法实例分析[2]表中第③栏是我国1978-2002年全社会客运量的资料,据期绘制散点图，见下图，可以看出，各年的客运量资料基本呈线性趋势，但在几个不同的时期直线有不同的斜率，因此考虑用变参数线性趋势模型进行预测。
具体步骤如下：表 我国1978-2002年全社会客运量及预测值 单位：万人年份 时间t 全社会客运量y 各期的一次指数平滑值 各期的二次指数平滑值a tb t① ② ③ ④ ⑤ ⑥ ⑦ ⑧ 253993.0 253993.0 1978 1 253993 253993.0 253993.0 253993.0 0.0 1979 2 289665 275396.2 266834.9 283957.5 12841.9 253993.0 1980 3 341785 315229.5 295871.7 334587.3 29036.7 296799.4 1981 4 384763 356949.6 332518.4 381380.8 36646.8 363624.0 1982 5 428964 400158.2 373102.3 427214.2 40583.9 418027.5 1983 6 470614 442431.7 414699.9 470163.4 41597.6 467798.1 1984 7 530217 495102.9 462941.7 527264.1 48241.8 511761.1 1985 8 620206 570164.8 527275.5 613054.0 64333.8 575505.81986 9 688212 640993.1 595506.1 686480.1 68230.5 677387.8 1987 10 746422 704250.4 660752.7 747748.2 65246.6 754710.7 1988 11 809592 767455.4 724774.3 810136.4 64021.6 812994.8 1989 12 791376 781807.8 758994.4 804621.1 34220.1 874158.1 1990 13 772682 776332.3 769397.1 783267.5 10402.8 838841.2 1991 14 806048 794161.7 784255.9 804067.6 14858.8 793670.2 1992 15 860855 834177.7 814209.0 854146.4 29953.1 818926.3 1993 16 99663 931651.5 884674.5 978628.5 70465.5 884099.5 1994 17 1092883 1028390.4 970904.0 1085876.8 86229.6 1049094.0 1995 18 1172596 1114913.8 1057309.9 1172517.6 86405.8 1172106.3 1996 19 1245356 1193179.1 1138831.4 1247526.8 81521.5 1258923.5 1997 20 1326094 1272928.0 1219289.4 1326566.7 80458.0 1329048.3 1998 21 1378717 1336401.4 1289556.6 1383246.2 70267.2 1407024.7 1999 22 1394413 1371208.4 1338547.7 1403869.1 48991.1 1453513.4 2000 23 1478573 1435627.1 1396795.4 1474458.9 58247.7 1452860.1第一步，计算一次指数平滑值。
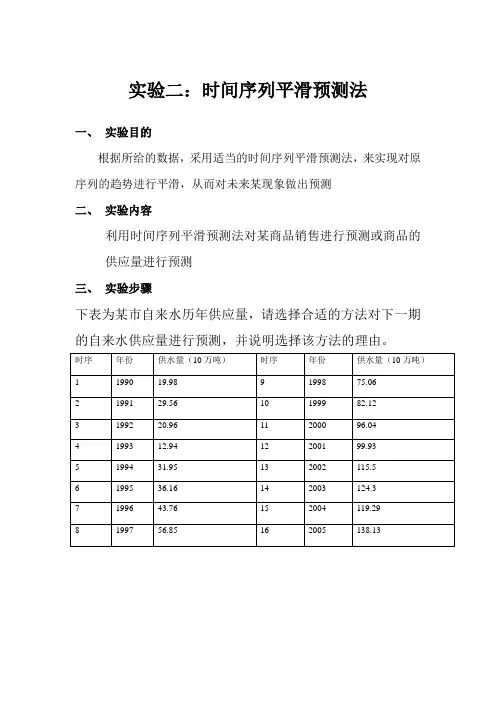
实验二：时间序列平滑预测法一、实验目的根据所给的数据，采用适当的时间序列平滑预测法，来实现对原序列的趋势进行平滑，从而对未来某现象做出预测二、实验内容利用时间序列平滑预测法对某商品销售进行预测或商品的供应量进行预测三、实验步骤下表为某市自来水历年供应量，请选择合适的方法对下一期的自来水供应量进行预测，并说明选择该方法的理由。
一：根据上表数据做出散点图如下：根据上图可以看出：从1993后时间序列具有明显的线性变化趋势，为了避免利用移动平均法预测有趋势的数据时产生的误差，所以不宜采用一次移动平均法及一次指数线性二次指数平滑法才能满足预测模型的要求二次曲线指数平滑法的计算过程如下： （1）计算t 时期的单指数平滑值)1(t s ：)1(1)1()1(--+=t t tS x S αα（2）计算t 时期的双指数平滑值)2(t s ：)2(1)1()2()1(--+=t ttS S S αα（3）计算t 时期的三重指数平滑值)3(t s ：)3(1)2()3()1(--+=t ttS S S αα（4）计算t 时期的水平值t A ：)3()2()1(33t ttt S S S A +-=（5）计算t 时期的线性增量t B ：])34()810()56[()1()3()2()1(22t t t t S S S B ααααα-+----= （6）计算t 时期的抛物线增量t C ：)2()1()3()2()1(22tt t t S S S C +--=αα （7）预测m 时期以后，即（t+m ）时期的数值m t F +：221m C m B A F t t t m t ++=+其中，m 是正整数，1≥m 。
二次曲线指数平滑法的初始值依赖于两个时期的观测值21x x 和。
已知21x x 和，假设：1)3(1)2(1)1(1x S S S ===。
根据表中的数据可知：各个时期的供水量变化很大，所以的值要选择大一些，本题选择的 5.0=α和8.0=α同时把第一期的值作为预测一次二次的初始预测值，所以其计算结果如下根据所给的数据，选取了三个不同的α值对该模型进行预测，具体计算数值通过计算机计算如下：（1）取二次曲线指数平滑法预测某市的供水量5.0=α时序 年份 供水量（10万吨）)1(t s)2(t s)3(t st At Bt C )1(=+m F m t1 1990 19.98 19.98 19.98 19.982 1991 29.56 24.77 22.38 21.18 28.363 5.39 1.2 3 1992 20.96 22.865 22.62 21.9 22.634 -0.9 -0.5 34.35 4 1993 12.94 17.903 20.26 21.08 14.004 -6.2 -1.5 21.45 5 1994 31.95 24.926 22.59 21.84 28.834 6.27 1.58 7.025 6 1995 36.16 30.543 26.57 24.2 36.127 8 1.61 35.89 7199643.76 37.152 31.86 28.03 43.906 8.95 1.4644.938 1997 56.86 47.006 39.43 33.73 56.451 12.3 1.87 53.599 1998 75.06 61.033 50.23 41.98 74.383 17.2 2.55 69.6410 1999 82.12 71.576 60.9 51.44 83.459 13.7 1.21 92.8311 2000 96.04 83.808 72.36 61.9 96.255 13.9 1 97.7612 2001 99.93 91.869 82.11 72.01 101.28 8.88 -0.4 110.713 2002 115.5 103.68 92.9 82.45 114.81 11.6 0.34 11014 2003 124.3 113.99 103.4 92.95 124.59 10.7 0.05 126.615 2004 119.29 116.64 110 101.5 121.29 1.72 -1.9 135.316 2005 138.13 127.39 118.7 110.1 136.12 8.83 0.06 12217 2006 1451-3（2）取8.0=α二次曲线指数平滑法预测某市的供水量8.0=α时序年份供水量（10万吨）)1(ts)2(ts)3(tstAtBtC)1(=+mFmt1 1990 19.98 19.98 19.98 19.982 1991 29.56 27.64 26.11 24.88 29.48 17.66 4.9053 1992 20.96 22.3 23.06 23.42 21.14 -15.1 -6.37 49.594 1993 12.94 14.81 16.46 17.85 12.9 -17.1 -4.11 2.8875 1994 31.95 28.52 26.11 24.46 31.7 34.92 12.18 -6.296 1995 36.16 34.63 32.93 31.23 36.35 11.18 0.17 72.77 1996 43.76 41.93 40.13 38.35 43.76 12.08 0.344 47.618 1997 56.86 53.87 51.13 48.57 56.82 22.55 3.099 56.019 1998 75.06 70.82 66.88 63.22 75.04 32.3 4.431 80.9110 1999 82.12 79.86 77.27 74.46 82.24 11.15 -3.41 109.611 2000 96.04 92.8 89.7 86.65 95.97 21.42 0.957 91.6812 2001 99.93 98.5 96.74 94.72 100 4.689 -4.12 117.913 2002 115.5 112.1 109 106.2 115.4 25.05 3.368 102.614 2003 124.3 121.9 119.3 116.7 124.4 14.91 -0.94 142.115 2004 119.29 119.8 119.7 119.1 119.4 -12.3 -8.07 138.816 2005 138.13 134.5 131.5 129 137.9 30.91 7.507 103.117 2006 172.51-4通过比较图1-2、1-3和1-4，我们可以看出当5.0α，预测线拟=合的数值更接近真实的观测值，而当8.0α时，预测值与实际观测值=偏差较大，故选取平滑常数5.0α，来对某市的自来水供水量进行逐=年预测。
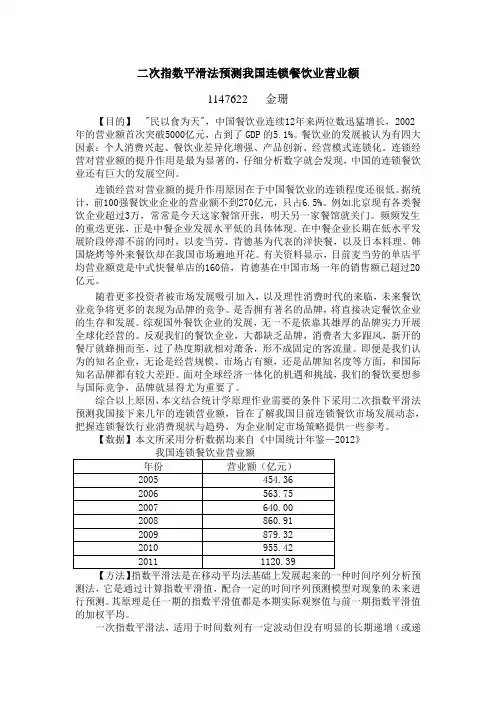
二次指数平滑法预测我国连锁餐饮业营业额1147622 金珊【目的】"民以食为天"，中国餐饮业连续12年来两位数迅猛增长，2002年的营业额首次突破5000亿元，占到了GDP的5.1%。
餐饮业的发展被认为有四大因素：个人消费兴起、餐饮业差异化增强、产品创新、经营模式连锁化。
连锁经营对营业额的提升作用是最为显著的，仔细分析数字就会发现，中国的连锁餐饮业还有巨大的发展空间。
连锁经营对营业额的提升作用原因在于中国餐饮业的连锁程度还很低。
据统计，前100强餐饮业企业的营业额不到270亿元，只占6.5%。
例如北京现有各类餐饮企业超过3万，常常是今天这家餐馆开张，明天另一家餐馆就关门。
频频发生的重迭更张，正是中餐企业发展水平低的具体体现。
在中餐企业长期在低水平发展阶段停滞不前的同时，以麦当劳、肯德基为代表的洋快餐，以及日本料理、韩国烧烤等外来餐饮却在我国市场遍地开花。
有关资料显示，目前麦当劳的单店平均营业额竟是中式快餐单店的160倍，肯德基在中国市场一年的销售额已超过20亿元。
随着更多投资者被市场发展吸引加入，以及理性消费时代的来临，未来餐饮业竞争将更多的表现为品牌的竞争。
是否拥有著名的品牌，将直接决定餐饮企业的生存和发展。
综观国外餐饮企业的发展，无一不是依靠其雄厚的品牌实力开展全球化经营的。
反观我们的餐饮企业，大都缺乏品牌，消费者大多跟风，新开的餐厅就蜂拥而至，过了热度期就相对萧条，形不成固定的客流量。
即便是我们认为的知名企业，无论是经营规模、市场占有额，还是品牌知名度等方面，和国际知名品牌都有较大差距。
面对全球经济一体化的机遇和挑战，我们的餐饮要想参与国际竞争，品牌就显得尤为重要了。
综合以上原因，本文结合统计学原理作业需要的条件下采用二次指数平滑法预测我国接下来几年的连锁营业额，旨在了解我国目前连锁餐饮市场发展动态，把握连锁餐饮行业消费现状与趋势，为企业制定市场策略提供一些参考。
【数据】本文所采用分析数据均来自《中国统计年鉴—2012》我国连锁餐饮业营业额年份营业额（亿元）2005 454.362006 563.752007 640.002008 860.912009 879.322010 955.422011 1120.39【方法】指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法，它是通过计算指数平滑值，配合一定的时间序列预测模型对现象的未来进行预测。
