同弧对应的圆周角和圆心角的关系

弧、弦、圆心角、圆周角--知识讲解（基础）责编：康红梅【学习目标】1.了解圆心角、圆周角的概念；2.理解圆周角定理及其推论，能灵活运用圆周角的定理及其推理解决有关问题；3.掌握在同圆或等圆中，三组量：两个圆心角、两条弦、两条弧，只要有一组量相等，就可以推出其它两组量对应相等，及其它们在解题中的应用．【要点梳理】要点一、弧、弦、圆心角的关系1.圆心角定义如图所示，∠AOB的顶点在圆心，像这样顶点在圆心的角叫做圆心角．2.定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．3.推论：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦也相等．在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧也相等．要点诠释：(1)一个角要是圆心角，必须具备顶点在圆心这一特征；(2)注意定理中不能忽视“同圆或等圆”这一前提.要点二、圆周角1.圆周角定义：像图中∠AEB、∠ADB、∠ACB这样的角，它们的顶点在圆上，并且两边都与圆相交的角叫做圆周角．2.圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．3.圆周角定理的推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．要点诠释：(1)圆周角必须满足两个条件：①顶点在圆上；②角的两边都和圆相交.(2)圆周角定理成立的前提条件是在同圆或等圆中.4.圆内接四边形：（1）定义: 圆内接四边形：顶点都在圆上的四边形，叫圆内接四边形．（2）性质：圆内接四边形对角互补，外角等于内对角（即它的一个外角等于它相邻内角的对角）．5.弦、弧、圆心角、弦心距的关系：在同圆或等圆中，弦，弧，圆心角，弦心距等几何量之间是相互关联的，即它们中间只要有一组量相等，(例如圆心角相等)，那么其它各组量也分别相等(即相对应的弦、弦心距以及弦所对的弧也分别相等)。

*如果它们中间有一组量不相等，那么其它各组量也分别不等。

第08讲圆心角与圆周角（核心考点讲与练）【知识梳理】一．圆心角、弧、弦的关系（1）定理：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等．（2）推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．说明：同一条弦对应两条弧，其中一条是优弧，一条是劣弧，而在本定理和推论中的“弧”是指同为优弧或劣弧．（3）正确理解和使用圆心角、弧、弦三者的关系三者关系可理解为：在同圆或等圆中，①圆心角相等，②所对的弧相等，③所对的弦相等，三项“知一推二”，一项相等，其余二项皆相等．这源于圆的旋转不变性，即：圆绕其圆心旋转任意角度，所得图形与原图形完全重合．（4）在具体应用上述定理解决问题时，可根据需要，选择其有关部分．二．圆周角定理（1）圆周角的定义：顶点在圆上，并且两边都与圆相交的角叫做圆周角．注意：圆周角必须满足两个条件：①顶点在圆上．②角的两条边都与圆相交，二者缺一不可．（2）圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．（3）在解圆的有关问题时，常常需要添加辅助线，构成直径所对的圆周角，这种基本技能技巧一定要掌握．（4）注意：①圆周角和圆心角的转化可通过作圆的半径构造等腰三角形．利用等腰三角形的顶点和底角的关系进行转化．②圆周角和圆周角的转化可利用其“桥梁”﹣﹣﹣圆心角转化．③定理成立的条件是“同一条弧所对的”两种角，在运用定理时不要忽略了这个条件，把不同弧所对的圆周角与圆心角错当成同一条弧所对的圆周角和圆心角．三．相交弦定理（1）相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等．（经过圆内一点引两条线，各弦被这点所分成的两段的积相等）．几何语言：若弦AB、CD交于点P，则P A•PB＝PC•PD（相交弦定理）（2）推论：如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项．几何语言：若AB是直径，CD垂直AB于点P，则PC2＝P A•PB（相交弦定理推论）．【核心考点精讲】一．圆心角、弧、弦的关系（共4小题）1．（2021•江北区校级开学）在⊙O中，如果＝2．那么弦AB与弦CD之间的关系是（）A．AB＝2CD B．AB＞2CD C．AB＜2CD D．无法确定2．（2020秋•靖江市期中）已知弦AB的长等于⊙O的半径，弦AB所对的圆周角是度．3．（2021•广州模拟）如图，AB，CD为⊙O内两条相交的弦，交点为E，且AB＝CD，求证：AD∥BC．4．（2022春•永嘉县月考）如图，AB是⊙O的直径，点C，E都在⊙O上，OC⊥AB，＝2，DE∥AB 交OC于点D，延长OC至点F，使FC＝OC，连接EF．（1）求证：CD＝OD．（2）若⊙O的直径是4，求EF的长．二．圆周角定理（共5小题）5．（2022•浦江县模拟）已知：如图，OA是⊙O的半径，若∠BAO＝27°，则圆周角∠BDA的度数是（）A．63°B．60°C．58°D．54°6．（2021秋•嘉兴期末）如图，AB是⊙O的直径，点C在圆上，若∠ABC＝70°，则∠BAC的度数为（）A．70°B．60°C．40°D．20°7．（2022•柯桥区一模）如图，在⊙O中，AD是直径，∠ABC＝35°，则∠CAD等于（）A．75°B．65°C．55°D．45°8．（2022•文成县一模）如图，点A，B，C都在⊙O上，∠AOC：∠BOC＝2：5，OA∥BC，则∠ABC＝°．9．（2021秋•嵊州市期末）已知：如图，在△ABC中，AB＝AC，以腰AB为直径作⊙O，分别交BC，AC 于点D，E，连结OD，DE．（1）求证：BD＝DC．（2）若∠BAC＝50°，求∠ODE的度数．三．相交弦定理（共2小题）10．（2021秋•东阳市月考）已知四边形ABCD两条对角线相交于点E，AB＝AC＝AD，AE＝3，EC＝1，则BE•DE的值为（）A．6B．7C．12D．1611．（2021秋•余姚市期中）如图，⊙O的弦AB、CD相交于点P，若AP＝6，BP＝8，CP＝4，则CD长为（）A．16B．24C．12D．不能确定【过关检测】一．选择题（共10小题）1．（2021秋•西城区校级期中）如图，在5×5正方形网格中，一条圆弧经过A、B、C三点，那么所对的圆心角的大小是（）A．60°B．75°C．80°D．90°2．（2022•富阳区一模）如图，AB是⊙O的直径，弦CD⊥AB于点E，G是弧AC上一点，连接AD，AG，GD，BC．则下列结论错误的是（）A．∠ADC＝∠AGDB．若∠ADC＝∠GAD，则＝2C．若＝，则△ADG是等腰三角形D．若＝，则△AGF是等腰三角形3．（2022•舟山二模）如图，BC是⊙O的直径，AD⊥BC，∠ABC＝25°，则弧CD的度数（）A．50°B．25°C．100°D．65°4．（2022•西湖区一模）如图，已知AB是⊙O的直径，弦CD与AB交于点E，设∠ABC＝α，∠ABD＝β，∠AEC＝γ，则（）A．α+β﹣γ＝90°B．β+γ﹣α＝90°C．α+γ﹣β＝90°D．α+β+γ＝180°5．（1999•山西）如图，⊙O中，弦AB和CD相交于P，CP＝2.5，PD＝6，AB＝8，那么以AP、PB的长为两根的一元二次方程是（）A．x2﹣8x﹣15＝0B．x2﹣8x+15＝0C．x2+8x﹣15＝0D．x2+8x+15＝06．（2022•鹿城区校级二模）如图，△ABC的两顶点A，B在⊙O上，点C在圆外，∠C＝46°，边AC交⊙O于点D，DE∥BC经过圆心交⊙O于点E，则的度数为（）A．44°B．80°C．88°D．92°7．（2022•黄岩区一模）如图，△ABC是等边三角形，点A，点B在数轴上，点A表示数﹣2，点B表示数2，以AB为直径作圆交边AC于点P，以B为圆心，BP为半径作弧交数轴于点Q，则点Q在数轴上表示的数为（）A．B．2C．2﹣2D．2﹣28．（2022•永康市模拟）如图，线段AB是⊙O的直径，点C在圆上，∠AOC＝60°，点P是线段AB延长线上的一点，连结PC，则∠APC的度数不可能是（）A．30°B．25°C．10°D．5°9．（2022•东坡区校级模拟）如图，AB为⊙O的直径，点D是弧AC的中点，过点D作DE⊥AB于点E，延长DE交⊙O于点F，若AC＝12，AE＝3，则⊙O的直径长为（）A．10B．13C．15D．1610．（2021秋•杭州期末）如图，AB，CD是⊙O的两条弦，它们相交于点P，连接AD、BD，已知AD＝BD＝4，PC＝6，那么CD的长为（）A．6B．7C．8D．9二．填空题（共4小题）11．（2021秋•亭湖区期末）如图，AB是⊙O的直径，＝＝，∠COD＝34°，则∠AEO的度数是．12．（2014秋•柯城区校级期中）如图，在⊙O中，弦AB，CD相交于点E，AE＝2cm，BE＝6cm，DE＝3cm，则CE＝cm；学以致用：点P是直径为10的⊙Q中一点且PQ＝2，过点P作弦HK，则线段PH 与线段PK的积等于．13．（2021秋•定海区期末）一块直角三角板的30°角的顶点A落在圆O上，两边分别交圆O于B、C两点，则弧BC的度数为．14．（2021秋•温州期末）如图，点A在半圆O上，BC是直径，．若AB＝2，则BC的长为．三．解答题（共6小题）15．（2021秋•淳安县期中）如图，在⊙O中，弦AD＝BC，连接AB、CD．求证：AB＝CD．16．（2021秋•上城区期中）如图，AD、BC是⊙O的两条弦，且AB＝CD，求证：AD＝BC．17．（2021秋•长兴县期中）如图，MB，MD是⊙O的两条弦，点A，C分别在，上，且AB＝CD，M是的中点．求证：MB＝MD．18．（2021秋•诸暨市期末）如图，O为半圆的圆心，C、D为半圆上的两点，连接CD、BD、AD，CD＝BD．连接AC并延长，与BD的延长线相交于点E．（1）求证：CD＝DE；（2）若AC＝6，半径OB＝5，求BD的长．19．（2021秋•滨江区期末）如图，在⊙O中，AB＝CD，弦AB与CD相交于点M．（1）求证：＝．（2）连接AC，AD，若AD是⊙O的直径，求证：∠BAC+2∠BAD＝90°．20．（2001•温州）⊙O的两条弦AB，CD交于点P，已知AP＝4，BP＝6，CP＝3，求CD的长．。

圆周角与圆心角关系的证明的三种情况的具体证法
已知在⊙O中，∠BOC与圆周角∠BAC同对弧BC，求证：∠BOC=2∠BAC. 证明：
情况1：，当圆心O在∠BAC的一边上时，即A、O、B在同一直线上时：
∵OA、OC是半径
∴OA=OC
∴∠BAC=∠ACO（等边对等角）
∵∠BOC是△OAC的外角
∴∠BOC=∠BAC+∠ACO=2∠BAC
情况2：，当圆心O在∠BAC的内部时：
连接AO，并延长AO交⊙O于D
∵OA、OB、OC是半径
∴OA=OB=OC
∴∠BAD=∠ABO，∠CAD=∠ACO（等边对等角）
∵∠BOD、∠COD分别是△AOB、△AOC的外角
∴∠BOD=∠BAD+∠ABO=2∠BAD
∠COD=∠CAD+∠ACO=2∠CAD
∴∠BOC=∠BOD+∠COD=2(∠BAD+∠CAD)=2∠BAC
情况3：，当圆心O在∠BAC的外部时：
连接AO，并延长AO交⊙O于D
∵OA、OB、OC、是半径
∴∠BAD=∠ABO（等边对等角）,∠CAD=∠ACO(OA=OC）∵∠DOB、∠DOC分别是△AOB、△AOC的外角
∴∠DOB=∠BAD+∠ABO=2∠BAD
∠DOC=∠CAD+∠ACO=2∠CAD
∵∠BAC=∠CAD-∠BAD
∠BOC=∠DOC-∠DOB=2(∠CAD-∠BAD)=2∠BAC。

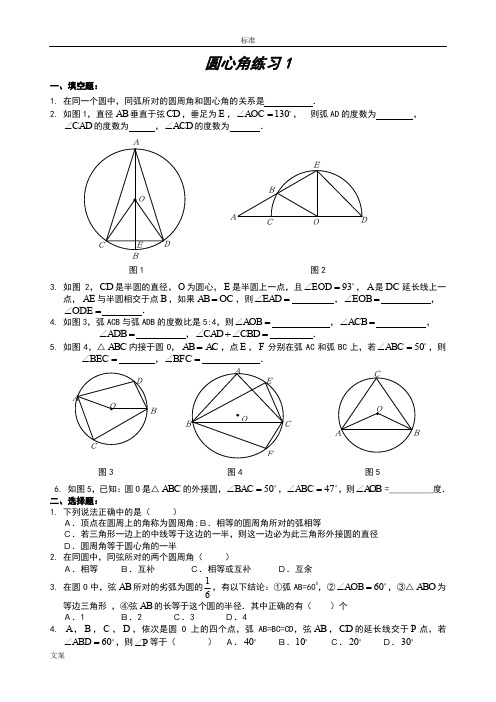
圆心角练习1一、填空题：1. 在同一个圆中，同弧所对的圆周角和圆心角的关系是．2. 如图1，直径AB 垂直于弦CD ，垂足为E ，130AOC ∠=， 则弧AD 的度数为，CAD ∠的度数为 ，ACD ∠的度数为 ．图1 图23. 如图2，CD 是半圆的直径，O 为圆心，E 是半圆上一点，且93EOD ∠=，A 是DC 延长线上一点，AE 与半圆相交于点B ，如果AB OC =，则EAD ∠= ，EOB ∠= ，ODE ∠= ．4. 如图3，弧ACB 与弧ADB 的度数比是5:4，则AOB ∠= ，ACB ∠= ，ADB ∠= ，CAD CBD ∠+∠= ． 5. 如图4，△ABC 内接于圆O ，AB AC =，点E ，F 分别在弧AC 和弧BC 上，若50ABC ∠=，则BEC ∠=，BFC ∠= ．图3 图4 图56. 如图5，已知：圆O 是△ABC 的外接圆，50BAC ∠=，47ABC ∠=，则A O B ∠=__________度． 二、选择题：1. 下列说法正确中的是（ ）Ａ．顶点在圆周上的角称为圆周角;Ｂ．相等的圆周角所对的弧相等Ｃ．若三角形一边上的中线等于这边的一半，则这一边必为此三角形外接圆的直径 Ｄ．圆周角等于圆心角的一半2. 在同圆中，同弦所对的两个圆周角（ ）Ａ．相等 Ｂ．互补 Ｃ．相等或互补 Ｄ．互余 3. 在圆O 中，弦AB 所对的劣弧为圆的16，有以下结论：①弧AB=600，②60AOB ∠=，③△ABO 为等边三角形 ，④弦AB 的长等于这个圆的半径．其中正确的有（ ）个 Ａ．1 Ｂ．2 Ｃ．3 Ｄ．44. A ，B ，C ，D ，依次是圆O 上的四个点，弧AB=BC=CD ，弦AB ，CD 的延长线交于P 点，若60ABD ∠=，则P ∠等于（） Ａ．40 Ｂ．10 Ｃ．20 Ｄ．305. 如图6，圆内接四边形ABCD 的对角线AC ，BD 把四边形的四个内角分成八个角，这八个角中相等的角的对数至少有（ ）Ａ．1对 Ｂ．2Ｄ．4对图6 图7 图8 图96. 如图7，AC 是圆O 的直径，AB ，CD 是圆O 的两条弦，且AB CD ∥．如果32BAC ∠=，则A O D ∠的度数是（ ） Ａ．16 Ｂ．32 Ｃ．48 Ｄ．64 7. 如图8，四边形ABCD 内接于圆O ，若100BOD ∠=，则DAB ∠的度数（ ）Ａ．50 Ｂ．80 Ｃ．100 Ｄ．1308. 如图9，D ，E 在以AB 为直径的半圆上，F ，C 在AB 上，CDEF 为正方形，若正方形边长为1，AC a =，BC b =，则下列式子中，不正确的是（ ） Ａ．1a b -= Ｂ．1ab = Ｃ．a b +=Ｄ．225a b +=三、解答题：1. 如图，BC 为圆O 的直径，AD BC ⊥，垂足为D ，A 是弧BF 的中点，BF 与AD 交于E ．（1）求证：AE BE =；（2）若A ，F 把半圆三等分，12BC =，求AE 的长．2．如图，AD 是⊙O 的直径，垂直于AD 的三条弦B 1C 1，B 2C 2，B 3C 3把圆周6等分，分别求∠B 1，∠B 2，∠B 3的度数；100ＤB C 2圆心角练习题2【模拟试题】（答题时间：）1. 在同圆或等圆中，如果两个圆心角、两条弧、或中有一组是相等的，那么，所对应的其余各组量都分别相等。

(教案)圆周角与圆心角、弧的关系一、知识讲解：1．圆周角与圆心角的的概念：顶点在圆上，同时两边都和圆相交的角叫做圆周角。

2．在同圆或等圆中，假如两条弦，两条弧，两个圆心角中有一组量相等，那么它们所对应的其它各组量都分别相等。

3．一条弧所对的圆周角等于这条弧所对的圆心角的一半。

4．直径所对的圆周角是90度，90度的圆周角所对的弦是直径。

5．圆的内接四边形对角之和是180度。

6．弧的度数确实是圆心角的度数。

解题思路：1．已知圆周角，能够利用圆周角求出圆心角2．已知圆心角，能够利用圆心角求出圆周角3．已知直径和弧度，能够求出圆周角与圆心角1.圆周角与圆心角的定义顶点在圆上，同时两边都和圆相交的角叫做圆周角。

注意圆周角定义的两个差不多特点：(1)顶点在圆上；(2)两边都和圆相交。

二、教学内容【1】圆心角：顶点在圆心的角。

利用两个错误的图形来强调圆周角定义的两个差不多特点：练习：判断下列各图形中的是不是圆周角，并说明理由．【2】明白得圆周角定理的证明一条弧所对的圆周角的度数等于这条弧所对的圆心角度数的一半。

已知：⊙O中，弧BC所对的圆周角是∠BAC，圆心角是∠BOC，求证：∠BAC= 1/2∠BOC.分析：通过图形的演示指导学生进一步去查找圆心O与∠BAC的关系本题有三种情形：（1）圆心O在∠BAC的一边上 O（2）圆心O在∠BAC的内部（3）圆心O在∠BAC的外部 B D C●假如圆心O在∠BAC的边AB上,只要利用三角形内角和定理的推论和等腰三角形的性质即可证明●假如圆心O在∠BAC的内部或外部,那么只要作出直径AD,将那个角转化为上述情形的两个角的和或差即可证明:圆心O在∠BAC的一条边上 AOA=OC==>∠C=∠BAC∠BOC=∠BAC+∠C O==>∠BAC=1/2∠BOC. B C【3】圆周角与圆心角的关系（1）．在同圆或等圆中，假如两条弦，两条弧，两个圆心角中有一组量相等，那么它们所对应的其它各组量都分别相等。