上海交通大学理论力学2006-2007学年期中试卷(含答案)81学时A卷
- 格式:pdf
- 大小:196.59 KB
- 文档页数:5

同济大学课程考核试卷(A 卷) 2006—2007学年第一学期命题教师签名:审核教师签名: 课号:课名:工程力学考试考查:此卷选为:期中考试()、期终考试()、重考()试卷 年级专业学号姓名得分=10m/s 2,成60度mm 计)2_;计的刚当无初B 的12C5均质细杆AB 重P ,长L ,置于水平位置,若在绳BC 突然剪断瞬时有角加速度?,则杆上各点惯性力的合力的大小为_gPL 2α,(铅直向上)_,作用点的位置在离A 端_32L_处,并在图中画出该惯性力。
6铅垂悬挂的质量--弹簧系统,其质量为m ,弹簧刚度系数为k ,若坐标原点分别取在弹簧静伸长处和未伸长处,则质点的运动微分方程可分别写成_0=+kx x m _和_mg kx x m =+ _。
二、计算题(10分)图示系统中,曲柄OA 以匀角速度?绕O 轴转动,通过滑块A 带动半圆形滑道BC 作铅垂平动。
已知:OA?=?r?=?10?cm ,??=?1?rad/s ,R?=?20?cm 。
试求??=?60°时杆BC 的加速度。
解:动点:滑块A ,动系:滑道BC ,牵连平动 由正弦定理得: 34.34=βcm/s 55.566.115sin 2r =︒=AA v v [5分]向ζ方向投影:2cm/s 45.7=[10分]三、计算题(15分)图示半径为R 的绕线轮沿固定水平直线轨道作纯滚动,杆端点D 沿轨道滑动。
已知:轮轴半径为r ,杆CD 长为4R ,线段AB 保持水平。
在图示位置时,线端A 的速度为v ,加速度为a,铰链C 处于最高位置。
试求该瞬时杆端点D 的速度和加速度。
解: 轮C 平面运动,速度瞬心P 点CO [8分](1) 物块下落距离时轮中心的速度与加速度; (2) 绳子AD段的张力。
解:研究系统:T 2-T 1=ΣW i223C v m +21J C ω2+21J B ω2+221A vm =m 1gs [5分] 式中:2321r m J C =,22ρm J B =代入得:v C =23222113222r m ρm R m gsm r++[7分]式两边对t 求导得:a C =23222113222r m ρm R m grRm ++[10分]对物A:m a=ΣF ,即:m 1a A =m 1g -F AD F AD =m 1g -m 1a A =m 1g -ra R m C⋅1[15分][15六、计算题(15分)在图示系统中,已知:匀质圆柱A 的质量为m1,半径为r ,物块B 质量为m 2,光滑斜面的倾角为?,滑车质量忽略不计,并假设斜绳段平行斜面。
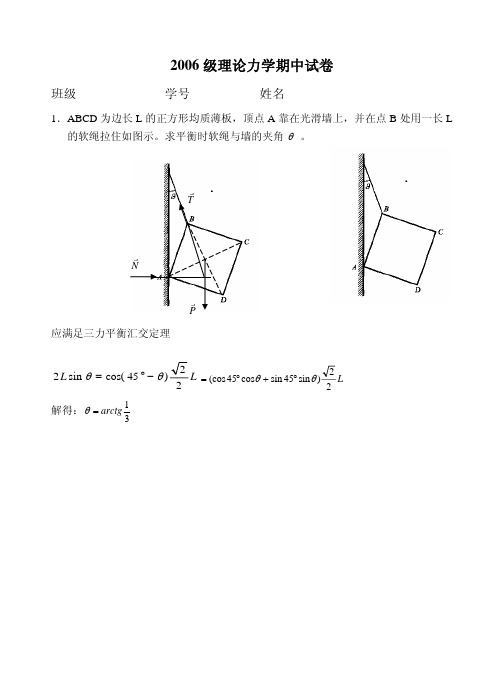
2006级理论力学期中试卷班级 学号 姓名1.ABCD 为边长L 的正方形均质薄板,顶点A 靠在光滑墙上,并在点B 处用一长L 的软绳拉住如图示。
求平衡时软绳与墙的夹角 。
θT r Pr Nr应满足三力平衡汇交定理 L L 22)45cos(sin 2θθ−°=L 22)sin 45sin cos 45(cos θθ°+°= 解得:31arctg =θ2.图示结构中,各杆自重不计。
已知:AB =CD =AD =L =6m ,=5kN /m ,M =18kN ·m ,P =20kN 。
试求A 、D 支座的反力及AC 杆的内力。
B q3.静定水平组合梁如图所示,已知AC=CD=DB=a=2m,CK=b,分布载荷的最大值q=1.960kN/m,重为G=5.880kN的物块E放置在粗糙的斜面上,物块与斜面间的摩擦系数f=0.3,并用细绳跨过定滑轮连接在CB杆的中点D上,不计梁的自重。
试求:(1)物体系统平衡时,b的取值范围;(2)当b=2m时,固定端A处的约束反力及重物E受到的摩擦力。
解:(1)取物块E为研究对象,设其有向下的滑动趋势,受力如图(a)所示,建立坐4.图是平面凸轮机构,已知:,,B O OA 1=1OO AB =s /rad o 2=ω,0=α,图示位置AB 水平,OA AB ⊥,,cm L 15=cm h 10=。
试求图示位置(1)DE 杆上D 点的速度;(2)D 点相对于曲柄OA 的速度。
5.平面机构如图所示。
已知OA杆以匀角速度ω绕O轴转动,与直角三角形板ABC铰接的滑块B被限制在水平轨道中,套筒C与板铰接,其中OA=R,DE穿过套筒C。
在图示位置时,OA杆铅垂,AB与DE平行,φ=30°。
试求该瞬时:(1)滑块B的加速度;(2)DE杆的角速度和角加速度。


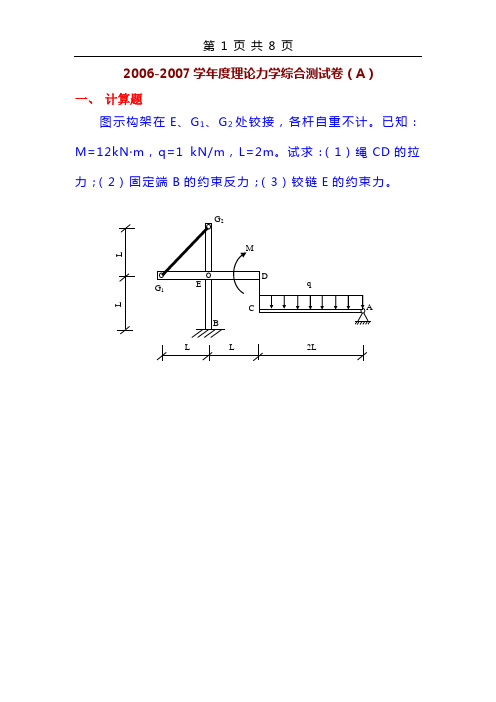
2006-2007学年度理论力学综合测试卷(A )一、 计算题图示构架在E 、G 1、G 2处铰接,各杆自重不计。
已知:M=12kN 〃m ,q=1 kN/m ,L=2m 。
试求:(1)绳CD 的拉力;(2)固定端B 的约束反力;(3)铰链E 的约束力。
二、 计算题质量为M ,半径为r 的均质圆柱体放在粗糙水平面上。
柱的外面绕有轻绳,绳子跨过一个很轻的滑轮,并悬挂一质量为m 的物体。
设圆柱体只滚不滑,并且圆柱体与滑轮间的绳子是水平的。
求圆柱体质心的加速度1a ,物体的加速度2a 及绳中张力T 。
m图五.3三、 计算题图示机构中,鼓轮A 和圆盘B 为均质,半径均为R ,重量各为P ,物体C 重为Q 。
若在A 上作用一力偶矩为M 的常值力偶,试求C 上升的加速度。
(绳与圆盘、鼓轮之间无相对滑动)四、计算题水平均质正方形板重P,用六根直杆固定在水平地面上,各杆两端均为球铰,试求各杆内力。
五、 计算题图示平面机构中,曲柄长为m r 2.0=,以匀角速度s rad /2=ω绕O 轴转动;连杆AB 长为m l 4.0=,通过销钉B 带动圆轮绕O 1轴转动,圆轮半径为mR 1.0=。
在图示位置时,求1)B 点的速度;2)B 点的加速度。
六、计算题已知Q =20kN,M = 8 kN〃m,q = 10 kN/m,a = 0.8m。
试用虚位移原理求支座B、C的反力。
七、计算题均质圆柱体位于铅直平面内,已知:圆柱的半径为R,重为Q,支座A和B的水平间距为L。
试用动静法求突然移去支座B的瞬时,圆柱质心C的加速度和支座A的反力。
八、计算题一组合梁ABC求固定端A的约束反力。
九、 计算题杆AB 长2m ,设A 端沿地面作匀速运动,sm v A/1 ,B 端沿斜面运动,求当θ=30º时B 点的速度与杆的角速度,B 点的加速度和杆的角加速度。
十、 计算题边长b =100mm 的正方形均质板重400N ,由三根绳拉住,如图所示。

2010 ~2011 学年度第 二 学期《 理论力学 》试卷(A 卷)一、填空题(每小题 4 分,共 28 分)1、如图1.1所示结构,已知力F ,AC =BC =AD =a ,则CD 杆所受的力F CD =( ),A 点约束反力F Ax =( )。
2、如图1.2 所示结构,,不计各构件自重,已知力偶矩M ,AC=CE=a ,A B ∥CD 。
则B 处的约束反力F B =( );CD 杆所受的力F CD =( )。
E 1.1 1.23、如图1.3所示,已知杆OA L ,以匀角速度ω绕O 轴转动,如以滑块A 为动点,动系建立在BC 杆上,当BO 铅垂、BC 杆处于水平位置时,滑块A 的相对速度v r =( );科氏加速度a C =( )。
4、平面机构在图1.4位置时, AB 杆水平而OA 杆铅直,轮B 在水平面上作纯滚动,已知速度v B ,OA 杆、AB 杆、轮B 的质量均为m 。
则杆AB 的动能T AB =( ),轮B 的动能T B =( )。
1.3 1.45、如图1.5所示均质杆AB 长为L ,质量为m,其A 端用铰链支承,B 端用细绳悬挂。
当B 端细绳突然剪断瞬时, 杆AB 的角加速度 =( ),当杆AB 转到与水平线成300角时,AB 杆的角速度的平方ω2=( )。
6、图1.6所示机构中,当曲柄OA 铅直向上时,BC 杆也铅直向上,且点B 和点O 在同一水平线上;已知OA=0.3m,BC=1m ,AB=1.2m,当曲柄OA具有角速度ω=10rad/s 时,则AB 杆的角速度ωAB =( )rad/s,BC 杆的角速度ωBC =( )rad/s 。
AB1.57、图1.7所示结构由平板1、平板2及CD 杆、EF 杆在C 、D 、E 、F 处铰接而成,在力偶M 的作用下,在图上画出固定铰支座A 、B 的约束反力F A 、F B 的作用线方位和箭头指向为( )(要求保留作图过程)。
1.7二、单项选择题(每小题 4 分,共28 分)1、如图2.1所示,四本相同的书,每本重均为P ,设书与书间的摩擦因数为0.1,书与手间的摩擦因数为0.25,欲将四本书一起抱起,则两侧手应加的压力至少大于( )。
上 海 交 通 大 学 理 论 力 学 试 卷 答 案 (51学时)1. 平衡系统由杆OA ﹑杆AD ﹑杆CD ﹑杆BC 和杆EG 组成,如图所示。
端O 为固定支座,A ﹑B ﹑C ﹑D ﹑E ﹑G 处为理想圆柱铰链。
不计各杆的重量。
图示位置OA ﹑AD 和BC 水平,CD 铅垂。
已知:2m OA AD CD BC ====, 杆AD 上作用一力偶,力偶矩大小为M = 2N.m 。
杆OA 上作用线性分布载荷, A 处的载荷集度为4 N/m 。
铰链E 和G 分别位于AD 和CD 的中点。
求:(1) 杆EG 的内力 (2) 固定支座O 处的约束力和约束力偶矩。
(20分)解:取AD ,CD ,EG 和BC 的一段为研究对象:()20ABC m F M =-=¥F , 1N BC F =0XAX BC F F F =-+=¥, 1N AX F =0YAY FF ==¥, 0AY F =取CD 以及EG 和BC的一段为研究对象:()20D BC EGm F F =-=¥F, N EG F =取OA 为研究对象:0XOX AXFF F ᄁ=+=¥, 1N OX F =-CDCqD0YOY FF Q =-=¥, 4NOY F Q ==4()03O O m M Q =-=¥F , 416N.m 33OM Q ==2. 如图所示,杆AO 和杆AB 重量不计,铰O 为固定铰支座,杆OA 与杆AB 以圆柱铰A 铰接,杆AB 的端B 搁置在粗糙的地面上,端B的极限摩擦系数为4。
杆AO 和杆AB 的长度均为l 。
大小为W 的集中载荷作用点在杆AB 的点C ,令点C 与点B 的距离为x ,杆AB 上作用一水平力F,大小为2W 。
求系统平衡时x 的范围。
(20分)F’AX==A2WA杆OA 是两力杆,设OA F 为两力杆的内力,取杆AB 为研究对象,对B点取矩1()022B OA xm F l F W=-+=¥v ,得到 OA xF W l=ᅲ0yN FF W =-=¥, N F W=当B点处于右滑的临界状态024X OA N F F F F W l m =-+=-+=�¥解得:4lx =当B点处于左滑的临界状态024X OA N F F F F W l m =--=--=�¥解得:34x l =系统平衡时x 的范围:1344l x l ᆪᆪA3. 如图所示,圆弧杆B 1搁置在高为h 的平台上。
同济大学课程考核试卷(A 卷)2006— 2007 学年第一学期命题教师签名:审核教师签名:课号:课名:工程力学考试考查:此卷选为:期中考试 ( ) 、期终考试 ()、重考 ( )试卷年级专业学号XX得分题号 一二 三 四五 六 总分题分 301015151515100得分一、 填空题(每题 5 分,共 30 分)1 刚体绕 O Z 轴转动,在垂直于转动轴的某平面上有 A ,B 两点,已知Z Z A2,方向如图所示。
则此时 B 点加速度的OA=2O B ,某瞬时 a =10m/s大小为 __5m/s 2z 度角。
;(方向要在图上表示出来)。
与 O B 成 602 刻有直槽 OB 的正方形板 OABC 在图示平面内绕 O 轴转动,点 M 以 r=OM =50t 2(r 以 mm 计)的规律在槽内运动,若2t ( 以rad/s 222中画出。
方向垂直 OB ,指向左上方。
3 质量分别为 m 1=m , m 2=2m 的两个小球 M 1, M 2用长为 L 而重量 不计的刚杆相连。
现将M 1置于光滑水平面上,且 M 1M 2与水平面成 60 角。
则当无初速释放, M 2球落地时, M 1球移动的水平距离为 ___(1) ___。
(1)L;(2)L;(3)L;(4)0。
3464 已知 OA=AB=L , =常数,均质连杆 AB 的质量为 m ,曲柄 OA ,滑块 B 的质量不计。
则图示瞬时,相对于杆 AB 的质心 C 的动量矩的大小为__ L CmL 2,(顺时针方向) ___。
125 均质细杆 AB 重 P ,长 L ,置于水平位置,若在绳 BC 突然剪断瞬时有角加速度 ,则杆上各点惯性力的合力的大小为_ PL,(铅直向上) _,作用点的位置在离 A 端_2L_处,并2g3在图中画出该惯性力。
6 铅垂悬挂的质量-- 弹簧系统,其质量为m ,弹簧刚度系数为k ,若坐标原点分别取在弹簧静伸长处和未伸长处,别写成 _ mx kx 0 _和_ mx kx mg _。
A 卷
1.图示构件自重不计,已知q =3kN/m ,F =4kN ,M =6kNm ,l =2m ,B 为光滑铰链。
试求固定端A 处的约束力。
解:以杆BC 为研究对象
∑=0)(F M B r
M l F C =⋅
23N ,kN 32332N ==l
M F C 以整体为研究对象
∑=0
x F
02
=⋅++l
q F F Ax
kN 72
−=⋅
−−=l
q F F Ax ∑=0y
F
0N =+y A C F F ,kN 32−=Ay F
∑=0)(F M A r
04
223N =+⋅⋅−−−⋅
A C M l
l q Fl M l F
kN 5.9=A M
2. 两个重量相同的物块A 和B ,用铰链和直杆连接如图所示。
物块A 和B 分别与铅垂面和水平面接触,当o
45=φ时,物块即将开始滑动。
如各摩擦面之间的摩擦系数相等,并且直杆的重量不计,求滑动摩擦系数s f 。
[解] AB 为两力杆,截断AB ,分别取物块A 和B 和AB 的一部分为研究对象 物块A 的平衡方程为
02
2
=−
S N A (1)
02
222=−+=−+
G S N f G S F A s Am (2) 物块B 的平衡方程为
02222=−=−B s Bm N f S F S (3) 02
2
=−−
G S N B (4) 由方程(1),(2),(3),(4)得到 0122
=−+s s f f 12−=
s f
3. 图示滑块A 用铰链连接在杆AB 的一端,杆AB 穿过可绕O 转动的套筒。
设m OE 3.0=。
滑块A 的速度为s m /8.0,加速度为0。
求当o
60=ϕ时 (1)套筒的角速度与杆AB 相对套筒运动的速度 (2)套筒的角加速度与杆AB 相对套筒运动的加速度
v 速度分析图
加速度分析图
[解] 取A 为动点,套筒为动参考系。
套筒作定轴转动,A 相对动参考系作直线运动。
m OE OA 32.03/2==
(1)速度分析
r A e A A v v
v v v
v +=
s m v v v A A r A /4.02
1
cos ==
=ϕ S’
s m v v v A A e A /34.02
3
sin ==
=ϕ 套筒角速度为
s rad OA
v e A O /2==
ω
(2)加速度分析
0=+++=c
A r A e A e A A a a a a a v v v v v αω
22/38.032.04s m OA a a AB
e A r A =×===ωω 2/6.14.0222s m v a a r A AB c A e A =××===ωα
套筒角加速度为
2/3
3
8s rad OA
a e
A
O =
=
αα
4. 半径为r 的圆轮以角速度为ω,角加速度为 α 绕轴B 转动,从而带动靠在轮上的AC 杆绕轴A 摆动,已知r AB 3=
,试求图示位置AC 杆的角速度和角加速度。
解:
如图建立定参考基e A r −和动参考基1
e A r −。
在动参考基1
e A r −考察动点O
r 1e ω1e t 1O O O O v v v v r r r r ++=
其中r v O ω=r ,0e
t 1=O v r 根据速度矢量三角形可得
r v v O O ω==e ω1,r v v O O ω==r 1。
或以上矢量方程在动基1
e A r −上的坐标方程
1y r
:o o 30cos 30cos e ω1O O v v −=−,r v v O O ω==e ω1
1x r
:o o 30sin 30sin e ω1r 1O O O v v v −=,r v O ω=r 1
加速度分析
C O O O O O O a a a a a a 1r 1e ω1e α1e t 1++++=r
r r r r
其中τn O O O a a a r r r +=,r a O 2
n ω=,r a O α=τ,0e t 1=O a ,2
2)2(22e ω1r r a O ωω=
⋅=,r r a C O 212
2ωωω
=⋅⋅
=
在动基1
e A r −上的坐标方程
1y r :o
o o o 60cos 30cos 30cos 60cos e ω11e α1τn O C O O O O a a a a a +−−=−−
r r a
O
αω+−=2
e α13
21
,212322e 11α
ωαα+−
==r r a O
5. 四连杆机构如图所示,已知曲柄OA 长为r ,连杆AB 长为r 2,摇杆B O 1长r 32。
在给定瞬时,四连杆机构运动到图示位置,O 点,B 点和1O 点位于同一水平线上,而曲柄OA 与水平线垂直。
如曲柄的角速度为0ω,角加速度为2
03ωα=。
求B 点的速度和加速度。
解:曲柄OA 和摇杆B O 1作定轴转动,连杆AB 作平面运动。
(1)速度分析和计算 A 点速度大小为:
0ωr v A =
方向垂直于OA 。
连杆AB 在该瞬时的瞬心为O 点,故连杆AB 的瞬时角速度为
0ωω==
r
v A
AB (逆时针) 则B 点的速度为
03ωωr OB v AB B =⋅=
方向如图所示。
(2)加速度分析与计算 A 点的加速度为:
t
n A A A a a a +=
其中:2
0n
ωr a A =,2
00t
3ωαr r a A =
=,方向如图示。
以A 点为基点求B 点的加速度,有
t
n t n t n BA BA A A B B a a a a a a +++=+
(1)
其中2012
n 2
3ωr B O v a B B
==,2
2n 2ωωr AB a AB BA =⋅= 将(1)式向垂直于t
BA a 的η轴投影,有
n n t n t 30sin 30cos 30cos 30sin BA A A B B a a a a a −+−=+o o o o
解得: 2
0t 2
15ωr a B −
=
2
2n 2t 57)()(ωr a a a B B B =+=。