第六章---聚合物的力学性能

DMA 测量形状记忆高聚物性能原理及应用聚合物材料的动态力学性能测试在外力作用下，对样品的应变和应力关系随温度等条件的变化进行分析，即为动态力学分析。

动态力学分析能得到聚合物的动态模量( E′)、损耗模量(E″)和力学损耗(tanδ)。

这些物理量是决定聚合物使用特性的重要参数。

同时，动态力学分析对聚合物分子运动状态的反应也十分灵敏，考察模量和力学损耗随温度、频率以及其他条件的变化的特性可得到聚合物结构和性能的许多信息，如阻尼特性、相结构及相转变、分子松弛过程、聚合反应动力学等。

实验原理高聚物是黏弹性材料之一，具有黏性和弹性固体的特性。

它一方面像弹性材料具有贮存械能的特性，这种特性不消耗能量；另一方面，它又具有像非流体静应力状态下的黏液，会损耗能量而不能贮存能量。

当高分子材料形变时，一部分能量变成位能，一部分能量变成热而损耗。

能量的损耗可由力学阻尼或内摩擦生成的热得到证明。

材料的内耗是很重要的，它不仅是性能的标志，而且也是确定它在工业上的应用和使用环境的条件。

如果一个外应力作用于一个弹性体，产生的应变正比于应力，根据虎克定律，比例常数就是该固体的弹性模量。

形变时产生的能量由物体贮存起来，除去外力物体恢复原状，贮存的能量又释放出来。

如果所用应力是一个周期性变化的力，产生的应变与应力同位相，过程也没有能量损耗。

假如外应力作用于完全黏性的液体，液体产生永久形变，在这个过程中消耗的能量正比于液体的黏度，应变落后于应力90o，如图2-61(a)所示。

聚合物对外力的响应是弹性和黏性两者兼有，这种黏弹性是由于外应力与分子链间相互作用，而分子链又倾向于排列成最低能量的构象。

在周期性应力作用的情况下，这些分子重排跟不上应力变化，造成了应变落后于应力，而且使一部分能量损耗。

图2-61(b)是典型的黏弹性材料对正弦应力的响应。

正弦应变落后一个相位角。

应力和应变可以用复数形式表示如下。

σ*=σ0exp(iωt)γ*=γ0 exp[i (ωt-δ) ]式中，σ0和γ0为应力和应变的振幅；ω是角频率；i是虚数。

聚合物材料的力学性能研究一、引言聚合物材料因其优异的物理性质和低成本的生产工艺在工业中被广泛使用，然而聚合物材料的力学性能成为了影响其应用范围的一个关键因素。

在工程应用中，聚合物材料必须具备一定的力学性能，例如强度、韧性、刚度等。

因此，研究聚合物材料的力学性能具有极其重要的意义。

本文将分别从强度、韧性和刚度三个方面探讨聚合物材料的力学性能研究。

二、聚合物材料的强度研究强度是指受力材料最大承受力的能力。

在聚合物材料中，强度受到化学结构、晶化程度和制备工艺等因素的影响。

其中，聚合物的化学结构对其强度性能的影响最大，因为它决定了聚合物的分子量、分子量分布和化学键的类型和数量。

此外，影响聚合物材料的强度还包括晶化程度和制备工艺等因素。

研究表明，化学结构和分子量是影响聚合物材料强度的最主要因素。

其中，分子量的大小和分子量分布的宽窄对聚合物材料的强度影响极大。

较高的分子量和较窄的分子量分布可以提高聚合物材料的强度。

而分子量过高或分子量分布过窄会导致聚合物材料的加工难度增加，从而影响其生产工艺。

此外，化学结构的差异也会对聚合物材料的强度产生不同的影响。

例如在聚乙烯和聚丙烯等同属于烯烃类聚合物材料中，不饱和度的增加会降低其强度，而在芳香族聚合物材料中，饱和度的增加反而会降低其强度。

三、聚合物材料的韧性研究韧性是指材料在受冲击载荷时形变和吸收能量的能力。

聚合物材料的韧性受到其结晶度、分子量和分子量分布等因素的影响。

研究表明，增加聚合物材料的结晶度可以提高其韧性。

这是由于高结晶度会使聚合物分子之间的相互作用变强，从而增加聚合物材料的强度和韧性。

分子量和分子量分布的影响也与强度类似，即分子量和分子量分布的增加可以提高聚合物材料的韧性，但过高的分子量和过窄的分子量分布会影响材料的加工和生产。

此外，制备工艺也对聚合物材料的韧性产生影响。

例如，在高速注塑成型中，熔融聚合物材料受到剪切力的作用，从而影响其晶化程度和结晶形态，进而影响聚合物材料的韧性。

高分子物理习题集-答案第一章高聚物的结构4、高分子的构型和构象有何区别？如果聚丙烯的规整度不高，是否可以通过单键的内旋转提高它的规整度？答：构型：分子中由化学键所固定的原子或基团在空间的几何排列。

这种排列是稳定的，要改变构型必须经过化学键的断裂和重组。

构象：由于单键内旋转而产生的分子在空间的不同形态。

构象的改变速率很快，构象时刻在变，很不稳定，一般不能用化学方法来分离。

不能。

提高聚丙烯的等规度须改变构型，而改变构型与改变构象的方法根本不同。

构象是围绕单键内旋转所引起的排列变化，改变构象只需克服单键内旋转位垒即可实现，而且分子中的单键内旋转是随时发生的，构象瞬息万变，不会出现因构象改变而使间同PP（全同PP）变成全同PP（间同PP）；而改变构型必须经过化学键的断裂才能实现。

5、试写出线型聚异戊二烯加聚产物可能有那些不同的构型。

答：按照IUPAC有机命名法中的最小原则，CH3在2位上，而不是3位上，即异戊二烯应写成CH2C3CH CH21234（一）键接异构：主要包括1，4-加成、1，2-加成、3，4-加成三种键接异构体。

CH2nCCH3CH CH21,4-加成CH2nCCH3CH CH21，2-加成CH2nC CH3CH CH23，4-加成（二）不同的键接异构体可能还存在下列6中有规立构体。

①顺式1，4-加成CH 2CH 2CH 2CH 2C CH 3C HCH 3C CH②反式1，4-加成2CH 2CH 2CH 2C CH 3C HCH 3C C③1，2-加成全同立构CH 2C C 3C C HHH HCH CH 2CH CH 3C C H HCH 2CHCH 3④1，2-加成间同立构CC 3CC HH H HCH 3C C H HCH 3RRRR=CHCH 2⑤3，4-加成全同立构CH 2C CH3C CC C HH H HC C H HCH 2C CH 3CH 2C CH3HH⑥3，4-加成间同立构C C CC HH H HC CH HRRRR=CH 2HH C 36．分子间作用力的本质是什么？影响分子间作用力的因素有哪些？试比较聚乙烯、聚氯乙烯、聚丙烯、聚酰胺（尼龙-66）、聚丙烯酸各有那些分子间作用力？ 答：分子间作用力的本质是：非键合力、次价力、物理力。

实验7 聚合物动态力学性能的测定聚合物材料，如塑料、橡胶、纤维及其复合材料等都具有粘弹性，用动态力学的方法研究聚合物材料的粘弹性，已证明是一种非常有效的方法。

材料的动态力学行为是指材料在振动条件下，即在交变应力（或交变应变）作用下作出的力学响应。

测定材料在一定温度范围内的动态力学性能的变化即为动态力学分析（dynamic mechanical thermal analysis, DMTA ）一、二、实验目的了解动态力学分析的测量原理及仪器结构。

了解影响动态力学分析实验结果的因素，正确选择实验条件。

掌握动态力学分析的试样制备及测试步骤。

掌握动态力学分析在聚合物分析中的应用。

实验原理聚合物的粘弹性是指聚合物既有粘性又有弹性的性质，实质是聚合物的力学松弛行为。

研究聚合物的粘弹性常采用正弦的交变应力，使试样产生的应变也以正弦方式随时间变化。

这种周期性的外力引起试样周期性的形变，其中一部分所做功以位能形式贮存在试样中，没有损耗，而另一部分所做功，在形变时以热的形式消耗掉。

应变始终落后应力一个相位，以拉伸为例，当试样受到交变的拉伸应力作用时，其交变应力和应变随时间的变化关系如下： 应力 )sin(0δϖσσ+=t (7-1))900(0<<δ应变t ϖεεsin 0= (7-2) 式中0σ和0ε为应力和形变的振幅；ω是角频率；δ是应变相位角。

式（7-1）和式（7-2）说明应力变化要比应变领先一个相位差δ，见图7.1。

图7.1 应力应变和时间的关系将式（7-1）展开为：δϖσδωσσsin cos cos sin 00t t += (7-3)即认为应力由两部分组成，一部分)cos sin (δϖσt 与应变同相位，另一部分)sin cos (0δϖσt 与应变相差2/π。

根据模量的定义可以得到两种不同意义的模量，定义'E 为同相位的应力和应变的比值，而''E 为相位差2/π的应力和应变的振幅的比值，即t E t E ϖεωεσcos ''sin '00+= （7-4）此时模量是一个复数，叫复数模量*E 。

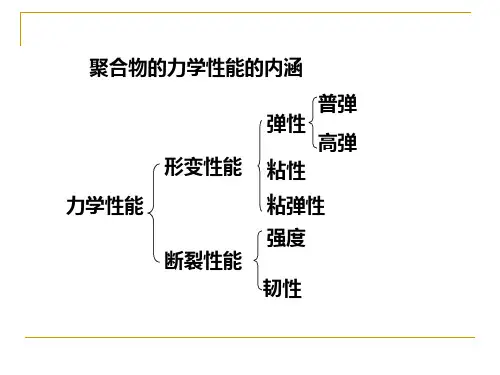
第六章高聚物的力学性能（1）6.1 概述6.1.1 高聚物力学性能的特点（形变性能、断裂性能）高弹形变：平衡高弹形变：瞬时、平衡、可逆的高弹形变；非平衡高弹形变：瞬时粘弹性，与时间有关高弹性：准平衡态高弹形变，由高分子构象熵的改变引起，处于链段无规自由热运动橡胶（弹性体）→外力作用（拉伸力）→ 链段运动对外响应→可逆的弹性形变（伸长数倍）普弹性：内能的改变引起粘弹性：呈粘性流体的性质、弹性和粘性同时出现。

表现在力学松弛现象（蠕变、应力松弛）及动态力学行为。

高聚物的力学行为：依赖于时间、温度。

必须同时考虑应力、应变、时间和温度来描述。

研究目的：（1）力学性能宏观描述和测试合理化；（2）宏观力学性能与微观各个层次的结构因素的关系。

6.1.2 形变类型和描述力学行为的基本物理量（1）简单剪切（形状改变，体积不变）剪切应力：σ = F/A，剪切应变：γ= tgθ，剪切模量（刚度）：G = σ/γ，剪切柔量：J = 1/G = γ/σ（2）本体（体积）压缩（形状不变，体积改变）本体应变：Δ= ΔV / V，本体模量：K = P/Δ = P / （- ΔV / V），本体柔量（可压缩度）：B = 1 / K（3）单向拉伸（形状和体积同时改变）拉伸应力：σ = F/A0（张应力，工程应力），拉伸应变：ε1 = （l-10）/10=Δl/10（张应力，工程应变，习用应变），杨氏模量：E = σ / ε1 （高聚物 E = 0.1MPa～500MPa），拉伸柔量：D = 1 / E横向应变：ε2 =（b - b0）/ b0，ε3 =（d - d0）/ d0）泊松比：γ = -ε2 / ε1= -ε3 / ε1 （拉伸试验中横向应变与纵向应变的比值的负数）对于大多数高聚物：橡胶，γ = 0.5，体积几乎不变，没有横向收缩。

塑料，γ = 0.2～0.4。

对各向同性的理想材料：G = E /（1+γ），K = E（1 - 2γ），E = 9KG /（3K + G），若体积几乎不变，即γ = 1/2, 则 E = 3G；对于各向异性材料情况比较复杂，不止有两个的独立弹性模量，通常至少有5或6个。

UNIT 22 Mechanical Properties of Polymers聚合物的力学性能The mechanical properties of polymers are of interest in all applications where polymers are used as structural materials. Mechanical behavior involves the deformation of a material under the influence of applied forces.聚合物的力学性能感兴趣的所有应用中聚合物被用作结构材料。

机械行为涉及材料形变的影响下，施加的力。

The most important and most characteristic mechanical properties are called moduli. A modulus is the ratio between the applied stress and the corresponding deformation. The re-ciprocals of the moduli are called compliances. The nature of the modulus depends on the na-ture of the deformation. The three most important elementary modes of deformation and the moduli (and compliances) derived from them are given in Table 22.1, where the definitions of the elastic parameters are also given. ® Other very important, but more complicated, de-formations are bending and torsion. From the bending or flexural deformation the tensile modulus can be derived. The torsion is determined by the rigidity.最重要和最具特色的机械特性被称为模。

实验七 聚合物的动态力学性能1. 实验目的要求1.1 掌握使用DMA Q800型动态力学分析仪测定聚合物的复合模量、储能模量和损耗模量的原理及方法。

1.2 能够通过数据分析，了解聚合物的结构特性。

2. 实验原理当样品受到变化着的外力作用时，产生相应的应变。

在这种外力作用下，对样品的应力-应变关系随温度等条件的变化进行分析，即为动态力学分析。

动态力学分析是研究聚合物结构和性能的重要手段，它能得到聚合物的储能模量（E '），损耗模量（E ''）和力学损耗（tan δ），这些物理量是决定聚合物使用特性的重要参数。

同时，动态力学分析对聚合物分子运动状态的反映十分灵敏，考察模量和力学损耗随温度、频率以及其它条件的变化的特性可得聚合物结构和性能的许多信息，如阻尼特性、相结构及相转变、分子松弛过程、聚合反应动力学等等。

本实验采用DMA Q800型动态力学分析仪分析聚合物在一定频率下，动态力学性能随温度的变化。

如果在试样上加一个正弦应力σ，频率为ω，振幅为0σ，则应变ε也可以以正弦方式改变，应力与应变之间有一相位差δ，可分别表示为：0sin t εεω=0sin()t σσωδ=+式中0σ和0ε分别为应力和应变的幅值，将应力表达式展开：00cos sin()sin cos t t σσδωδσδω=++应力波可分解为两部分，一部分与应力同相位，峰值为0cos σδ，与储存的弹性能有关，另一部分与应变有90°的相位差，峰值为0sin σδ，与能量的损耗有关。

定义储能模量（E '），损耗模量（E ''）和力学损耗（tan δ）：00(/)cos E σεδ'= 00(/)sin E σεδ''=sin tan cos E E δδδ''=='复数模量可表示为：*E E iE '''=+其绝对值为：E =在交变应力作用下，样品在每一周期内所损耗的机械能可通过下式计算：320()()W t d t E φεσπε''∆==∆与E''成正比，因此，样品损耗机械能的能力高低可以用E''或tanδ值的大小来W衡量。

聚合物材料的力学性能研究聚合物材料是一类由单体通过化学反应聚合而成的高分子化合物。

这类材料具有许多独特的性质和应用，如良好的绝缘性能、化学稳定性、低密度和优异的可加工性。

在工程领域，聚合物材料被广泛用于制造塑料制品、弹性体、纤维、涂料等。

力学性能是指材料在受力作用下的变形和破坏行为，对于聚合物材料的研究来说尤为重要。

常见的力学性能包括弹性模量、屈服强度、断裂韧性等。

聚合物材料的弹性模量决定了其在外力作用下的变形程度。

一般来说，聚合物材料的弹性模量较低，具有较大的变形能力，但也容易产生形状变化，导致塑性变形。

弹性模量的研究可以通过拉伸试验等方式进行，通常采用简单的胡克定律来描述其应力-应变关系。

聚合物材料的屈服强度是指在受到一定应力作用下，材料开始产生可观察的塑性变形的应力。

屈服强度的高低决定了材料的抗拉强度和抗压强度。

聚合物材料的屈服强度受到多个因素的影响，包括分子量、分子结构、结晶度、加工工艺等。

通过拉伸试验和压缩试验，可以评估聚合物材料的屈服强度。

聚合物材料的断裂韧性是指在拉伸或冲击等断裂试验中，材料能够吸收的能量。

良好的断裂韧性意味着材料在承受冲击或拉伸载荷时，能够有效地吸收能量，从而减少破裂的发生和传播。

断裂韧性的研究主要通过冲击试验和断裂韧性试验等手段进行。

除了上述几个常见的力学性能外，聚合物材料的研究还可以涉及到材料的硬度、粘弹性、疲劳性等其他方面。

材料硬度是指材料在受到外力作用下的抵抗程度，一般通过硬度试验来进行评估。

粘弹性是指材料同时具有粘性和弹性的特性，这种特性体现在材料在应力施加后，会存在一定程度的延迟才能恢复到初始状态。

疲劳性是指材料在反复加载下的变形和破坏行为，这可以通过疲劳实验来研究。

在聚合物材料的力学性能研究中，常常需要考虑到各种因素的影响，如温度、湿度、应变速率等。

这些因素会对聚合物材料的性能产生显著影响，因此需要进行相应的实验和分析。

综上所述，聚合物材料的力学性能研究是一个复杂而重要的领域，对于深入了解聚合物材料的应用性能、设计新材料以及改进加工工艺具有重要意义。

第六章聚合物的⼒学性能第六章聚合物的⼒学性能对于⼤部分应⽤⽽⾔，⼒学性能⽐⾼聚物的其它物理性能显得更为重要。

⾼聚物作为材料使⽤时，⼈们⾸先关⼼的是它们是否牢固、耐⽤。

⼒学性能中有两种“性能”：⼀个是着重于物理特性的“基本性能”；另⼀个是着重于实际应⽤的“技术性能”。

这两者之间并不⽭盾。

但为了弄清这两者之间的关系，⾸先有必要深⼊了解⾼聚物的基本⼒学性能，然后，再弄清⼯业测试中选择这种或那种⽅法的原因。

§1 聚合物⼒学⾏为的特点及其表征⼀．聚合物⼒学性能特点1. ⼒学性能可变范围宽。

橡胶—塑料—纤维，为不同的应⽤提供了⼴阔的选择余地。

2. 强度低、模量低。

但由于其重量轻，故⽐强度⾼（强度/密度）。

3.⼒学性能与各种结构因素有关。

除化学结构外，包括：分⼦量及其分布、⽀化和交联、结晶度和结晶形态、共聚⽅式、分⼦取向、增塑及填料等。

从⽽也受加⼯条件及使⽤环境的影响。

4.⾼弹性和粘弹性。

⾼聚物极⼤的分⼦量以及分⼦链构象变化所导致的柔性，使⾼聚物具有独特的⾼弹性。

5. 对于⾼聚物来说，存在多种运动单元，尤其分⼦链由⼀种构象过渡到另⼀种构象所需时间很长。

因为链段⽐⼩分⼦⼤得多，内摩擦⼒也⼤，具有明显的松弛特性。

所以，其⼒学性能强烈地依赖于温度和受⼒时间。

⼆、三种基本形变类型及其相互关系⼒学⾏为是指施加⼀个外⼒在材料上，它产⽣怎样的形变（或称响应）。

a)简单切变切应变r=tanθ, 切应⼒σ=F/A,切变模量G=σ/r, 切变柔量J＝1/G，当r→0, G→∞材料越硬。

切变时，物体只改变形状，⽽不改变体积。

聚合物各种运动单元对切变敏感，故它是⼀种重要的研究⼒学⾏为的形变类型。

b) 均匀压缩)//(0V V P B ?=本体在流体静压⼒下，⽆论固体、流体或粘弹性，它们的⼒学⾏为都⽆甚差异，故在聚合物⼒学⾏为研究中⼀般不采⽤。

c) 简单拉伸拉伸应⼒0A F =σ（习⽤应⼒），AF =真σ习⽤应变（伸长率）000l ll l l ?=-=ε， 0ln 0l ll dl ll ii ==?真ε对于较⼤的形变：ll ?=真ε或3/]1[2λλ-，ελ+=1 +-+-=-3224321εεελl l=λ（拉伸⽐）杨⽒模量εσ=E （虎克定律），柔量ED 1=。