河北省2019届中考数学系统复习 第六单元 圆 滚动小专题(八)三角形的外心与内心课件

第二节三角形的基本概念及全等三角形三角形三边关系(2次)1．(2019河北15题3分)如图(1)，M是铁丝AD的中点，将该铁丝首尾相接折成△ABC，且∠B＝30°，∠C＝100°，如图(2)．则下列说法正确的是( C )A．点M在AB上B．点M在BC的中点处C．点M在BC上，且距点B较近，距点C较远D．点M在BC上，且距点C较近，距点B较远2．(2019河北10题3分)已知三角形三边长分别为2，x，13，若x为正整数，则这样的三角形个数为( B )A．2个B．3个C．5个D．13个3．(2019邢台模拟)下列各组数中，能成为一个三角形的三条边长的是( A )A．2，3，4 B．2，2，4 C．1，2，3 D．1，2，64．(2019邯郸模拟)三角形的两边长分别为3和6，第三边的长是方程x2－6x＋8＝0的一个根，则这个三角形的周长是( D )A．2或4 B．11或13 C．11 D．13三角形内外角关系(2次)5．(2019河北4题2分)如图，平面上直线a，b分别过线段OK的两端点(数据如图)，则a，b相交所成的锐角是( B )A．20° B．30° C．70° D．80°,(第5题图)) ,(第6题图)) 6．(2019北京朝阳外国语学校一模)将一副直角三角板按如图所示叠放在一起，则图中∠α的度数是( C )A．45° B．60° C．75° D．90°7．(2019河北19题4分)如图，已知∠AOB＝7°，一条光线从点A出发后射向OB边．若光线与OB 边垂直，则光线沿原路返回到点A，此时∠A＝90°－7°＝83°.当∠A<83°时，光线射到OB边上的点A1后，经OB反射到线段AO上的点A2，易知∠1＝∠2.若A1A2⊥AO，光线又会沿A2→A1→A原路返回到点A，此时∠A＝__76__°.……若光线从点A发出后，经若干次反射能沿原路返回到点A，则锐角∠A的最小值＝__6__°.三角形的四条重要线段(2次)8．(2019河北9题3分)图示为4×4的格图，A，B，C，D，O均在格点上，点O是( B )A．△ACD的外心 B．△ABC的外心C．△ACD的内心 D．△ABC的内心(第8题图)(第9题图)9．(2019河北2题2分)如图，在△ABC中，D，E分别是边AB，AC的中点．若DE＝2，则BC＝( C )A．2 B．3 C．4 D．5全等三角形(7次)10．(2019唐山一模)在△ABC中，∠ABC＝30°，AB边长为10，AC边的长度可以在3、5、7、9、11中取值，满足这些条件的互不全等的三角形的个数是( D )A．3个 B．4个 C．5个 D．6个11．(2019邯郸模拟)如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为点D，交AC于点E，∠A＝∠ABE，若AC＝5，BC＝3，则BD的长为( D )A．2.5 B．1.5 C．2 D．112．(2019河北21题9分)如图，点B，F，C，E在直线l上(F，C之间不能直接测量)，点A，D在l异侧，测得AB＝DE，AC＝DF，BF＝EC.(1)求证：△ABC≌△DEF；(2)指出图中所有平行的线段，并说明理由．解：(1)∵BF＝EC，∴BF＋FC＝EC＋CF，即BC＝EF.又AB＝DE，AC＝DF，∴△ABC≌△DEF；(2)∵AB∥DE，AC∥DF.理由如下：∵△ABC≌△DEF，∴∠ABC＝∠DEF，∠ACB＝∠DFE.∴AB∥DE，AC∥DF.13．(2019唐山二模)如图，点E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，求证：AB＝DC.证明：∵BE＝CF，∴BF＝CE，又∵∠A＝∠D，∠B＝∠C，∴△ABF≌△DCE，∴AB＝DC.,中考考点清单)三角形分类及三边关系1．三角形分类(1)按角分类锐角三角形直角三角形钝角三角形(2)按边分类两条边相等的三角形三边相等的三角形三边互不相等的三角形__等腰__三角形__等边__三角形 不等边三角形2．三边关系：三角形任意两边之和__大于__第三边，任意两边之差小于第三边，如图，__a ＋b__>c ，|a －b|<__c__．3．判断几条线段能否构成三角形：运用三角形三边关系判定三条线段能否构成三角形，并不一定要列出三个不等式，只要两条较短的线段长度之和大于第三条线段的长度即可判断这三条线段能构成一个三角形．三角形内角和定理及内外角关系4．内角和定理：三角形的内角和等于__180°__．5．内外角关系：三角形的一个外角__等于__与它不相邻的两个内角之和．三角形的一个外角大于任何一个和它不相邻的内角．三角形中的四条重要线段6.四线 定义性质 图形中线连接一个顶点与它对边中点的线段 BD ＝DC高线 从三角形一个顶点到它对边所在直线的垂线段AD⊥BC， 即∠ADB＝ ∠ADC ＝90°续表角平 分线 一个内角的平分线与这个角的对边相交，顶点与交点之间的线段 ∠1＝∠2中 位 线连接三角形两边中点的线段DE∥BC 且DE ＝12BC全等三角形及其性质7．定义：能完全重合的两个三角形叫做全等三角形．8．性质：(1)全等三角形的对应边__相等__，对应角__相等__．(2)全等三角形的对应线段(角平分线、中线、高线、中位线)相等，对应__周长__相等，对应面积__相等__．全等三角形的判定(高频考点)全等三角形的证明及性质是河北中考的必考点，单独考查过，考查方式均为在解题过程中利用三角形全等的证明及性质得到相关结论．涉及到的背景有：①与三角形结合；②与四边形结合；③与圆结合．每年都在图形的平移、旋转及位似等图形变换的猜想证明题中考查，设问方式为证明线段之间的数量关系．9．三角形全等的判定类型 图形 已知条件 是否全等形成结论一般 三角 形的 判定A 1B 1＝A 2B 2， B 1C 1＝B 2C 2， A 1C 1＝A 2C 2是SSS∠B 1＝∠B 2， B 1C 1＝B 2C 2， ∠C 1＝∠C 2 是 ASA∠B 1＝∠B 2， ∠C 1＝∠C 2， A 1C 1＝A 2C 2 是 AASA 1B 1＝A 2B 2， ∠B 1＝∠B 2， B 1C 1＝B 2C 2 是 __SAS__续表直角 三角 形的 判定A 1B 1＝A 2B 2， A 1C 1＝A 2C 2，是____HL__【方法技巧】证明三角形全等的思路判定三角形全等⎩⎪⎪⎨⎪⎪⎧已知两边⎩⎪⎨⎪⎧找夹角→SAS 找直角→HL 或SAS找另一边→SSS已知一边和一角⎩⎪⎨⎪⎧边为角的对边→找任一角→AAS 边为角的邻边⎩⎪⎨⎪⎧找夹角的另一边→SAS 找夹边的另一角→ASA找边的对角→AAS 已知两角⎩⎪⎨⎪⎧找夹边→ASA 找任一边→AAS,中考重难点突破)三角形三边之间的关系【例1】(2019长沙中考)若一个三角形的两边长分别为3和7，则第三边长可能是( ) A ．6 B ．3 C ．2 D ．11 【学生解答】A【点拨】利用三边之间的关系：两边之和大于第三边及两边之差小于第三边来解答．1．(2019玉林中考)在等腰△ABC 中，AB ＝AC ，其周长为20 cm ，则AB 边的取值范围是( B ) A ．1 cm<AB<4 cm B ．5 cm<AB<10 cm C ．4 cm<AB<8 cm D ．4 cm<AB<10 cm三角形内角和，外角与内角的关系【例2】(2019乐山中考)如图，CE 是△ABC 的外角∠ACD 的平分线，若∠B＝35°，∠ACE ＝60°，则∠A＝( )A ．35°B ．95°C ．85°D ．75° 【学生解答】C【点拨】利用角平分线的定义可求得∠ACD 的度数，从而利用三角形的外角等于和它不相邻的两个内角的和求解．2．(2019临沂中考)如图，直线AB∥CD，∠A ＝40°，∠D ＝45°，则∠1的度数等于( B ) A ．80° B ．85° C ．90° D ．95°(第2题图)(第3题图)3．(2019原创)如图，CD 是△ABC 外角∠ACE 的平分线，AB ∥CD ，∠A ＝50°，则∠B 的大小是( A )A ．50°B ．60°C ．40°D ．30°全等三角形的性质与判定【例3】(2019沧州八中一模)如图，在Rt △ABC 中，∠ACB ＝90°，点D 、F 分别在AB 、AC 上，CF ＝CB ，连接CD ，将线段CD 绕点C 按顺时针方向旋转90°后得CE ，连接EF.(1)求证：△BCD≌△FCE；(2)若EF∥CD，求∠BDC 的度数．【解析】(1)由旋转的性质可得：CD ＝CE ，再根据同角的余角相等可证明∠BCD＝∠FCE，再根据全等三角形的判定方法即可证明△BCD≌△FCE；(2)由(1)可知△BCD≌△FCE，所以∠BDC＝∠E，易求∠E＝90°，进而可求出∠BDC 的度数．【学生解答】(1)∵将线段CD 绕点C 按顺时针方向旋转90°后得CE ，∴CD ＝CE ，∠DCE ＝90°，又∵∠ACB＝90°，∴∠BCD ＝90°－∠ACD＝∠FCE，在△BCD 和△FCE 中，⎩⎪⎨⎪⎧CB ＝CF ，∠BCD ＝∠FCE，CD ＝CE ，∴△BCD ≌△FCE(SAS)；(2)由(1)可知△BCD≌△FCE，∴∠BDC ＝∠E，∵EF ∥CD ，∴∠E ＝180°－∠DCE＝90°，∴∠BDC ＝90°.4．(2019武汉中考)如图，点B ，E ，C ，F 在同一条直线上，AB ＝DE ，AC ＝DF ，BE ＝CF ，求证：AB∥DE.证明：∵BE ＝CF ， ∴BE ＋EC ＝CF ＋EC. 即BC ＝EF ，∵AB ＝DE ，AC ＝DF ， ∴△ABC ≌△DEF(SSS)， ∴∠B ＝∠DEF， ∴AB ∥DE.5．(2019邯郸二十三中一模)如图，BD ⊥AC 于点D ，CE ⊥AB 于点E ，AD ＝AE ，求证：BE ＝CD. 证明：∵BD⊥AC，CE ⊥AB ， ∴∠ADB ＝∠AEC＝90°，在△ADB 和△AEC 中，⎩⎪⎨⎪⎧∠ADB ＝∠AEC，AD ＝AE ，∠A ＝∠A，∴△ADB ≌△AEC(ASA)，∴AB ＝AC ，又∵AD＝AE ，∴AB －AE ＝AC －AD. 即BE ＝CD.,中考备考方略)1．(2019南通中考)下列长度的三条线段能组成三角形的是( A )A ．5，6，10B ．5，6，11C ．3，4，8D ．4a ，4a ，8a(a>0)2．如图，AD ，AE 分别是△ABC 的高和角平分线，且∠B＝76°，∠C ＝36°，则∠DAE 的度数为( A )A ．20°B ．18°C ．38°D ．40°(第2题图)(第3题图)3．(2019石家庄模拟)一副三角板有两个直角三角形，如图叠放在一起，则∠α的度数是( A ) A．165° B．120° C．150° D．135°4．(2019河北石家庄四十三中一模)已知三角形两边长分别为3和8，则该三角形第三边的长可能是( B )A．5 B．10 C．11 D．125．(2019河北保定十三中一模)如图，AB∥CD，∠A＋∠E＝75°，则∠C为( C )A．60° B．65°C．75° D．80°6．(2019内江中考)将一副直角三角板如图放置，使含30°角的三角板的直角边和含45°角的三角板一条直角边在同一条直线上，则∠1的度数为( A )A．75° B．65° C．45° D．30°(第6题图)(第7题图)7．(2019哈尔滨中考)如图，在Rt△ABC中，∠BAC＝90°，将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′，点C的对应点是C′)，连接CC′，若∠CC′B′＝32°，则∠B的大小是( C )A．32° B．64° C．77° D．87°8．(2019永州中考)如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB＝AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD( D )A．∠B＝∠C B．AD＝AEC．BD＝CE D．BE＝CD(第8题图)(第9题图)9．(2019枣庄中考)如图，在△ABC中，AB＝AC，∠A＝30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D等于( A )A ．15°B ．17.5°C ．20°D ．22.5°10．(2019保定二模)如图，△ABC 和△ADE 都是等腰直角三角形，∠BAC ＝∠DAE＝90°，四边形ACDE 是平行四边形，连接CE 交AD 于点F ，连接BD 交CE 于点G ，连接BE ，下列结论中：①CE ＝BD ；②△ADC 是等腰直角三角形；③△AEC≌△AEB；④△CGD∽△CDF，一定正确的结论有( D )A ．1个B ．2个C ．3个D ．4个(第10题图)(第11题图)11．(2019东莞中考)如图，△ABC 三边的中线AD ，BE ，CF 的公共点G ，若S △ABC ＝12，则图中阴影部分面积是__4__．12．(2019重庆中考)如图，在△ABC 和△CED 中，AB ∥CD ，AB ＝CE ，AC ＝CD ，求证：∠B＝∠E. 证明：∵AB∥CD，∠DCA＝∠CAB. 又∵AB＝CE ，AC ＝CD ， ∴△CAB ≌△DCE(SAS)， ∴∠B ＝∠E.13．(2019原创)如图，∠ACB ＝90°，D 为AB 的中点，连接DC 并延长到E ，使CE ＝13CD ，过点B 作BF∥DE，与AE 的延长线交于点F.若AB ＝6，则BF 的长为( C )A ．6B ．7C ．8D ．10(第13题图)(第14题图)14．(2019石家庄模拟)如图，已知△ABC 的面积为10 cm 2，BP 为∠ABC 的平分线，AP 垂直BP 于点P ，则△PBC 的面积为( B )A ．4 cm 2B ．5 cm 2C ．6 cm 2D ．7 cm 215．(2019滨州中考)如图，在△ABC 中，D 为AB 上一点，E 为BC 上一点，且AC ＝CD ＝BD ＝BE ，∠A ＝50°，则∠CDE 的度数为( D )A ．50°B ．51°C ．51.5°D ．52.5°(第15题图)(第16题图)16．(2019常德中考)如图，在△ABC 中，∠B ＝40°，三角形的外角∠DAC 和∠ACF 的平分线交于点E ，则∠AEC＝__70__°.17．(2019南充中考)已知△ABN 和△ACM 位置如图所示，AB ＝AC ，AD ＝AE ，∠1＝∠2. 求证：(1)BD ＝CE ； (2)∠M＝∠N.证明：(1)∵在△ABD 和△ACE 中， ⎩⎪⎨⎪⎧AB ＝AC ，∠1＝∠2，AD ＝AE ，∴△ABD ≌△ACE(SAS)． ∴BD ＝CE ；(2)∵△ABD≌△ACE，∴∠ADB ＝∠AEC. 又∵∠MDO＝∠ADB，∠NEO ＝∠AEC， ∴∠MDO ＝∠NEO，∵∠MOD ＝∠NOE，∴180°－∠MDO －∠MOD＝180°－∠NEO－∠NOE，故∠M＝∠N.18．(2019绍兴中考)如果将四根木条首尾相连，在相连处用螺钉连接，就能构成一个平面图形． (1)若固定三根木条AB ，BC ，AD 不动，AB ＝AD ＝2 cm ，BC ＝5 cm ，如图，量得第四根木条CD ＝5 cm ，判断此时∠B 与∠D 是否相等，并说明理由；(2)若固定二根木条AB ，BC 不动，AB ＝2 cm ，BC ＝5 cm ，量得木条CD ＝5 cm ，∠B ＝90°，写出木条AD 的长度可能取到的一个值；(直接写出一个即可)(3)若固定一根木条AB 不动，AB ＝2 cm ，量得木条CD ＝5 cm ，如果木条AD ，BC 的长度不变，当点D 移到BA 的延长线上时，点C 也在BA 的延长线上，当点C 移到AB 的延长线上时，点A ，C ，D 能构成周长为30 cm 的三角形，求出木条AD ，BC 的长度．解：(1)相等．如图，连接AC ，∵AB ＝DA ＝2，BC ＝CD ＝5，AC ＝AC ， ∴△ABC ≌△ADC ，∠B ＝∠D；(2)答案不唯一，只要满足29－5≤AD≤29＋5即可，如AD ＝5 cm ； (3)设AD ＝x cm ，BC ＝y cm ，根据题意得 当点C 在点D 的右侧时 ⎩⎪⎨⎪⎧x ＋2＝y ＋5，x ＋（y ＋2）＋5＝30，解得⎩⎪⎨⎪⎧x ＝13，y ＝10，当点C 在点D 的左侧时， ⎩⎪⎨⎪⎧y ＝x ＋5＋2，x ＋（y ＋2）＋5＝30，解得⎩⎪⎨⎪⎧x ＝8，y ＝15， ∴5＋8<17，∴不合题意． ∴AD ＝13 cm ，BC ＝10 cm.19．(2019内江中考)问题引入：(1)如图①，在△ABC 中，点O 是∠ABC 和∠ACB 平分线的交点，若∠A＝α，则∠BOC＝__90°＋α2__(用α表示)；如图②，∠CBO ＝13∠ABC ，∠BCO ＝13∠ACB ，∠A ＝α，则∠BOC＝__120°＋α3__(用α表示)；(2)如图③，∠CBO ＝13∠DBC ，∠BCO ＝13∠ECB ，∠A ＝α，请猜想∠BOC＝__120°－α3__(用α表示)，并说明理由；类比研究：(3)BO ，CO 分别是△ABC 和外角∠DBC，∠ECB 的n 等分线，它们交于点O ，∠CBO ＝1n∠DBC ，∠BCO＝1n ∠ECB ，∠A ＝α，请猜想∠BOC＝__n －1n ·180°－αn__．解：(2)理由：∠BOC＝180°－(∠OBC＋∠OCB)＝180°－13(∠DBC＋∠ECB)＝180°－13(180°＋∠A)＝120°－α3.2019-2020学年数学中考模拟试卷一、选择题1．若关于x 的方程3x 2﹣2x+m ＝0的一个根是﹣1，则m 的值为（ ） A ．﹣5B ．﹣1C ．1D ．52．如图是二次函数y ＝ax 2+bx+c 的部分图象，由图象可知，满足不等式ax 2+bx+c ＞0的x 的取值范围是（ ）A.﹣1＜x ＜5B.x ＞5C.x ＜﹣1且x ＞5D.x ＜﹣1或x ＞53．已知P 是反比例函数8(0)y x x=>图象上一点，点B 的坐标为（1，0），A 是y 轴正半轴上一点，且AP⊥BP ，AP ：BP ＝1：2，那么四边形AOBP 的面积为（ ）A.6.5B.8C.10D.74．方程1235x x =+的解为( ). A ．1x =-B ．0x =C ．3x =-D ．1x =5．如图，在平面直角坐标系xOy 中，已知正比例函数11y k x =的图象与反比例函数22k y x=的图象交于(4,2)A --，(4,2)B 两点，当12y y >时，自变量x 的取值范围是（ ）A ．4x >B ．40x -<<C ．4x <-或04x <<D ．40x -<<或4x >6．如图，在ABC ∆中，AB AC =，点D 在AC 上，//DE AB ，若160CDE ∠=︒，则B Ð的度数为（ ）A ．80︒B ．75︒C ．65︒D ．60︒7．如图，矩形ABCD 中，AB ＝3，BC ＝5，点P 是BC 边上的一个动点（点P 不与点B 、C 重合），现将△PCD 沿直线PD 折叠，使点C 落到点C′处；作∠BPC′的角平分线交AB 于点E ．设BP ＝x ，BE ＝y ，则下列图象中，能表示y 与x 的函数关系的图象大致是（ ）A ．B ．C ．D ．8．“十•一”黄金周期间，某风景区在7天假期中，共接待游客的人数（单位：万人）统计如下表： 日期 10月1日 10月2日 10月3日 10月4日 10月5日 10月6日 10月7日 人数1.222.521.220.6其中众数和中位数分别是（ ） A ．1.2，2 B ．2，2.5C ．2，2D ．1.2，2.59．已知x+1x=6，则x 2+21x =（ ）A.38B.36C.34D.3210．有甲、乙两个不同的水箱，容量分别为a 升和b 升，且已各装了一些水．若将甲中的水全倒入乙箱之后，乙箱还可以继续装20升水才会满；若将乙箱中的水倒入甲箱，装满甲箱后，乙箱里还剩10升水，则a ，b 之间的数量关系是( ) A ．b ＝a+15B ．b ＝a+20C ．b ＝a+30D ．b ＝a+4011．给出四个实数3，13，0，-3，其中无理数是（ ） A ．3B ．13C ．0D ．-312．如图，直线y=-x+2分别交x 轴、y 轴于点A ，B ，点D 在BA 的延长线上，OD 的垂直平分线交线段AB 于点C ．若△OBC 和△OAD 的周长相等，则OD 的长是( )A ．2B ．22C ．522D ．4二、填空题13．如图，半径为13的等圆⊙O 1和⊙O 2相交与A ，B 两点，延长O 1O 2与⊙O 1交于点D ，连接BD 并延长与⊙O 2交于点C ，若AB ＝24，则CD ＝_____．14．分解因式:23m m -=________.15．分解因式：22x y -=_______________. 16．不等式组的解集是_____．17．如图，△AOB 中，∠O=90°，AO=8cm ，BO=6cm ，点C 从A 点出发，在边AO 上以2cm/s 的速度向O 点运动，与此同时，点D 从点B 出发，在边BO 上以1.5cm/s 的速度向O 点运动，过OC 的中点E 作CD 的垂线EF ，则当点C 运动了__s 时，以C 点为圆心，1.5cm 为半径的圆与直线EF 相切．18．分解因式： 24x x +=________________ 三、解答题19．先化简：(x+2+342x x +-)÷2692x x x ++-，然后判断当x=2sin60o －3时，原式取值的正负情况. 20．如图，在四边形ABCD 中，AC 平分∠BAD ，∠ABC ＝90°，AC ＝AD ＝2，M 、N 分别为AC 、CD 的中点，连接BM 、MN 、BN ． (1)求证：BM ＝MA ；(2)若∠BAD ＝60°，求BN 的长；(3)当∠BAD ＝ °时，BN ＝1．(直接填空)21．如图，在Rt △ABC 中，∠C ＝90°，以AC 为直径作⊙O ，交AB 于D ．(1)在图(1)中，用直尺和圆规过点D 作⊙O 的切线DE 交BC 于点E ；(保留作图痕迹，不写作法) (2)如图(2)，如果⊙O 的半径为3，ED ＝4，延长EO 交⊙O 于F ，连接DF ，与OA 交于点G ，求OG 的长．22．自习课上小明在准备完成题目：化简：（ x 2+6x+8)-（6x+8x 2+2）发现系数“ ” 印刷不清楚、 （1）他把“”猜成6，请你帮小明完成化简：（6x 2+6x+8)-（6x+8x 2+2)；（2）小明同桌看到他化简的结果说：“你猜错了，我看到该题标准答案的结果是常数。

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==初中数学知识点：三角形的内心、外心、中心、重心三角形的四心定义：1、内心：三角形三条内角平分线的交点，即内切圆的圆心。

内心是三角形角平分线交点的原理：经圆外一点作圆的两条切线，这一点与圆心的连线平分两条切线的夹角(原理：角平分线上点到角两边距离相等)。

2、外心：是三角形三条边的垂直平分线的交点，即外接圆的圆心。

外心定理：三角形的三边的垂直平分线交于一点。

该点叫做三角形的外心。

3、中心：三角形只有五种心重心、垂心、内心、外心、旁心，当且仅当三角形是正三角形的时候，四心合一心，称做正三角形的中心。

4、重心：重心是三角形三边中线的交点。

三角形的外心的性质：1.三角形三条边的垂直平分线的交于一点，该点即为三角形外接圆的圆心;2三角形的外接圆有且只有一个，即对于给定的三角形，其外心是唯一的，但一个圆的内接三角形却有无数个，这些三角形的外心重合;3.锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心与斜边的中点重合。

在△ABC中4.OA=OB=OC=R5.∠BOC=2∠BAC，∠AOB=2∠ACB，∠COA=2∠CBA6.S△ABC=abc/4R三角形的内心的性质：1.三角形的三条角平分线交于一点，该点即为三角形的内心2.三角形的内心到三边的距离相等，都等于内切圆半径r3.r=2S/(a+b+c)4.在Rt△ABC中，∠C=90°，r=(a+b-c)/2.5.∠BOC = 90 °+∠A/2 ∠BOA = 90 °+∠C/2 ∠AOC = 90 °+∠B/26.S△=[(a+b+c)r]/2 (r是内切圆半径)三角形的垂心的性质:1.锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外。

河北省2019届中考数学系统复习第六单元圆滚动小专题（八）三角形的内心与外心练习编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（河北省2019届中考数学系统复习第六单元圆滚动小专题（八）三角形的内心与外心练习）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为河北省2019届中考数学系统复习第六单元圆滚动小专题（八）三角形的内心与外心练习的全部内容。

滚动小专题（八) 三角形的外心与内心类型1三角形外心1．已知在△ABC中，AB＝3，BC＝4,AC＝5，则△ABC的外心在(D)A．△ABC内B．△ABC外C．BC边中点D．AC边中点2．(2018·河北模拟）如图，每个小三角形都是正三角形，则△ABC的外心是（B）A．D点B．E点C．F点D．G点3．如图，点O是正八边形ABCDEFGH的中心，则下列说法错误的是(C)A．O是△CEF的外心B．O是△CFG的外心C．O是△OAC的外心D．O是△CDE的外心4．如图是10个相同的正六边形紧密排列在同一平面上的情形．根据图中各点的位置，判断O 点是下列哪一个三角形的外心（C）A．△AB D B．△BCD C．△ACD D．△ADE5．某地有四个村庄E，F,G，H(其位置如图所示），现拟建一个电视信号中转站，信号覆盖的范围是以发射台为圆心的圆形区域．为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小(圆形区域半径越小，所需功率越小)，此中转站应建在（C）A．线段HF的中点处B．△GHE的外心处C．△HEF的外心处D．△GEF的外心处6．在△ABC中，O是它的外心，BC＝24 cm，O到BC的距离是5 cm，则△ABC的外接圆半径为(C）A．11 cm B．12 cm C．13 cm D．14 cm 7．如图，在平面直角坐标系xOy中，点A，B,P的坐标分别为(1，0)，（2，5），（4，2)．若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心，则点C的坐标为(7，4)或(6，5)或（1，4）．8．如图,在△ABC中,∠BAC＝70°,AB＝AC，O为△ABC的外心,△OCP为等边三角形，OP与AC 相交于点D，连接OA.（1)求∠OAC的度数；（2）求∠AOP的度数．解：(1)∵O为△ABC的外心，∴AO垂直平分BC。

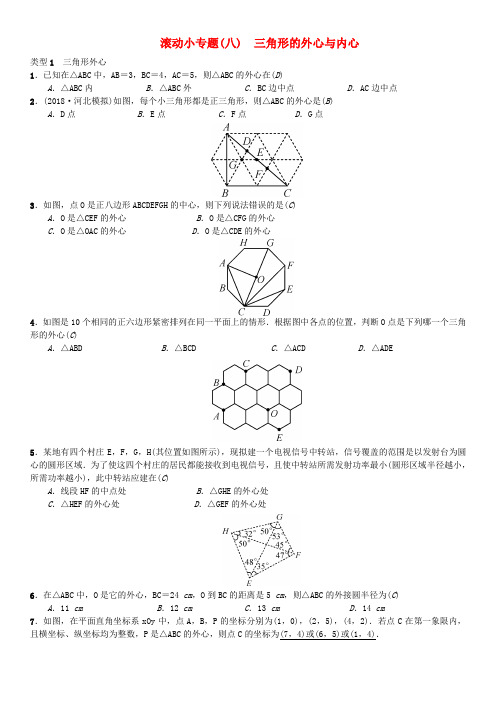
滚动小专题(八) 三角形的外心与内心类型1三角形外心1．已知在△ABC中，AB＝3，BC＝4，AC＝5，则△ABC的外心在(D)A．△ABC内B．△ABC外C．BC边中点D．AC边中点2．(2018·河北模拟)如图，每个小三角形都是正三角形，则△ABC的外心是(B)A．D点B．E点C．F点D．G点3．如图，点O是正八边形ABCDEFGH的中心，则下列说法错误的是(C)A．O是△CEF的外心B．O是△CFG的外心C．O是△OAC的外心D．O是△CDE的外心4．如图是10个相同的正六边形紧密排列在同一平面上的情形．根据图中各点的位置，判断O点是下列哪一个三角形的外心(C)A．△ABD B．△BCD C．△ACD D．△ADE5．某地有四个村庄E，F，G，H(其位置如图所示)，现拟建一个电视信号中转站，信号覆盖的范围是以发射台为圆心的圆形区域．为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小(圆形区域半径越小，所需功率越小)，此中转站应建在(C)A．线段HF的中点处B．△GHE的外心处C．△HEF的外心处D．△GEF的外心处6．在△ABC中，O是它的外心，BC＝24 cm，O到BC的距离是5 cm，则△ABC的外接圆半径为(C) A．11 cm B．12 cm C．13 cm D．14 cm7．如图，在平面直角坐标系xOy中，点A，B，P的坐标分别为(1，0)，(2，5)，(4，2)．若点C在第一象限内，且横坐标、纵坐标均为整数，P是△ABC的外心，则点C的坐标为(7，4)或(6，5)或(1，4)．8．如图，在△ABC 中，∠BAC＝70°，AB ＝AC ，O 为△ABC 的外心，△OCP 为等边三角形，OP 与AC 相交于点D ，连接OA.(1)求∠OAC 的度数； (2)求∠AOP 的度数．解：(1)∵O 为△ABC 的外心， ∴AO 垂直平分BC. ∵AB＝AC ，∴AO 平分∠BAC. ∴∠OAC＝12∠BAC＝35°.(2)∵O 为△ABC 的外心， ∴AO＝CO.∴∠OAC＝∠OCA＝35°.∴∠AOC＝110°. ∵△OCP 为正三角形，∴∠POC＝60°. ∴∠AOP＝50°.类型2 三角形内心9．如图为5×5的网格图，点A ，B ，C ，D ，O 均在格点上，则点O 是(B )A ．△ACD 的外心B ．△ABC 的外心 C ．△ACD 的内心 D ．△ABC 的内心10．如图，△ABC 是等腰直角三角形，点D ，E 在BC 上，△ADE 是等边三角形．若点O 是△ABC 的内心，则下列说法正确的是(C )A ．点O 是△ADE 的内心B ．点O 是△ADE 的外心C ．点O 不是△ABE 的内心D ．点O 是△ABC 的外心提示：易知OA平分∠BAC，由于OA不平分∠BAE，所以点O不是△ABE的内心．11．如图，I点为△ABC的内心，D点在BC上，且ID⊥BC.若∠B＝44°，∠C＝56°，则∠AID的度数为(A) A．174° B．176° C．178° D．180°提示：连接CI，∠AID＝∠AIC＋∠CID＝112°＋62°＝174°.12．如图，△ABC中，AB＝7 cm，AC＝8 cm，BC＝6 cm，点O是△ABC的内心，过点O作EF∥AB，与AC，BC分别交于点E，F，则△CEF的周长为(A)A．14 cm B．15 cm C．13 cm D．10.5 cm提示：连接OA，OB.C△CEF＝CE＋CF＋EF＝CE＋EA＋CF＋FB＝CA＋CB＝14 cm.13．如图，I是△ABC的内心，AI的延长线和△ABC的外接圆相交于点D，连接BI，BD，DC.下列说法中错误的一项是(D)A．线段DB绕点D顺时针旋转一定能与线段DC重合B．线段DB绕点D顺时针旋转一定能与线段DI重合C．∠CAD绕点A顺时针旋转一定能与∠DAB重合D．线段ID绕点I顺时针旋转一定能与线段IB重合提示：根据I是△ABC的内心，得到AI平分∠BAC，BI平分∠ABC，由角平分线的定义得到∠BAD＝∠CAD，∠AB I ＝∠CBI.根据三角形外角的性质得到∠DBI＝∠DIB，根据等腰三角形的性质得到BD＝DI.14．(2018·娄底)如图，P是△ABC的内心，连接PA，PB，PC，△PAB，△PBC，△PAC的面积分别为S1，S2，S3.则S1＜S2＋S3.(填“＜”“＝”或“＞”)15．如图所示，在Rt △ABC 中，∠ACB＝90°，在斜边AB 上分别截取AD ＝AC ，BE ＝BC ，DE ＝6，点O 是△CDE 的外心，则点O 到△ABC 的三边的距离之和是9．提示：由题意知：点O 是EC ，CD 垂直平分线的交点，∵AD＝AC ，BE ＝BC ，∴EC 的垂直平分线经过点B 且平分∠B，CD 的垂直平分线经过点A 且平分∠A.∴点O 是△ABC 的内心．∵∠ACB＝90°，∴r＝12(AC ＋BC －AB)＝12(AD ＋BE －AB)＝12DE ＝3.∴点O 到△ABC 的三边的距离之和是3r ＝9.16．三角形内角平分线的交点为三角形的内心．如图，D 是△ABC 的内心，E 是△ABD 的内心，F 是△BDE 的内心．若∠BFE 的度数为整数，则∠BFE 至少是113°．17．已知I 是△ABC 的内心，AI 的延长线交△ABC 的外接圆于点D ，连接BD.(1)在图1中，求证：DB ＝DI ；(2)如图2，若AB 为直径，且OI⊥AD 于点I ，DE 切圆于点D ，求sin ∠ADE 的值．解：(1)证明：连接BI. ∵I 是△ABC 的内心，∴AD 平分∠CAB，BI 平分∠ABC. ∴∠CAD＝∠BAD，∠ABI＝∠CBI. ∵∠CAD＝∠DBC，∴∠DAB＝∠DBC. ∵∠DBI＝∠DBC＋∠CBI， ∠DIB＝∠DAB＋∠ABI， ∴∠DIB＝∠DBI.∴DB＝DI. (2)连接BD ，DO.∵AB 为直径，∴∠ADB＝90°. ∵OI⊥AD，∴AD＝2DI. ∵BD＝DI ，∴AD＝2BD.∴AB＝AD 2＋BD 2＝5BD.∵DE 切圆于点D ，∴∠ADE＋∠ADO＝90°.又∵∠ADO＋∠ODB＝90°，∠ODB＝∠OBD， ∴∠ABD＝∠ADE.∴sin ∠ADE＝sin ∠ABD＝AD AB ＝2BD 5BD ＝255.。

第24讲与圆有关的位置关系命题点近8年的命题形式考查方向作为圆的核心知识点的补充，在中考范围内仅出点与圆的位置关系2021(T23(3)解) 现一次(2021年)，并巧妙结合外心与扇形相关内容进行考查，估计这种形式将偶尔出现.高频考点切线的性质与判定是河北省中考必考202 1(T25解)，2021(T23解)，(半圆202 1(T25解)，2021(T26考点，呈现方式稳定，多以局部圆为背景切线的性质与判定解)，或扇形，弓形等)，以旋转或折叠等方式，在变2021(T25解)，2021(T24解)，化过程中，对某一位置或某一时刻形成相切时，2021(T25解)，2021(T25解)对对应的某一量进行求解，表达了从一般到特殊，再到一般的研究问题的思维过程.常考点作为圆的核心知识点的补充，近四年出2021(T15选，T23(3)解)，三角形的内心与外心2021(T23(3)解)，2021(T9选)，现在中考试题中，既表达考查知识的连续性，又2021(T6选) 表达考查知识的全面性，估计这种全局设计方式在一定时期内将一直存在.命题点1 三角形的内心与外心1．(2021·河北T6·3分)如图，AC，BE是⊙O的直径，弦AD与BE相交于点F，以下三角形中，外心不是点O的是(B)A．△ABE B ．△ACF C．△ABD D ．△ADE2．(2021·河北T9·3分)如图为4×4的网格图，A，B，C，D，O均在格点上，点O是(B)A．△ACD的外心 B ．△ABC的外心C．△ACD的内心 D ．△ABC的内心3．(2021·河北T15·2分)如图，点I为△ABC的内心，AB＝4，AC＝3，BC＝2，将∠ACB平移使其顶点与I重合，那么图中阴影局部的周长为(B)1A．B．4C．3D．2命题点2切线的性质与判定︵4．(2021·河北T24·11分)如图，在△OAB中，OA＝OB＝10，∠AOB ＝80°，以点O为圆心，6为半径的优弧MN分别交OA，OB于点M，N.点P在右半弧上(∠BOP是锐角)，将OP绕点O逆时针旋转80°得OP′.求证：AP＝BP′；︵点T在左半弧上，假设AT与MN相切，求点T到OA的距离；︵(3)设点Q在优弧MN上，当△AOQ的面积最大时，直接写出∠BOQ的度数．解：(1)证明：∵∠AOP＝∠AOB＋∠BOP＝80°＋∠BOP，∠BOP′＝∠POP′＋∠BOP＝80°＋∠BOP，∴∠AOP＝∠BOP′.又∵OA＝OB，OP＝OP′，∴△AOP≌△BOP′(SAS)．AP＝BP′.连接OT，过点T作TH⊥OA于点H.︵∵AT与MN相切，∴∠ATO＝90°.∴＝2－2＝102－62＝8.ATOA OT1 12OA·TH＝2AT·OT，AT·OT8×624∴TH＝OA＝10＝5.24∴点T到OA的距离为5.(3)10°或170°.(注：当OQ⊥OA时，△AOQ的面积最大，且左右两半弧上各存在一点)重难点1 切线的性质如图，AB是⊙O的直径，且长为10，点P是AB下方的半圆上不与点 A，B重合的一个动点，点C为AP的中点，延长CO交⊙O于点D，连接AD，过点D作⊙O的切线交PB的延长线于点E，连CE.︵(1)假设∠ADC＝30°，求BD的长；(2)求证：△DAC≌△ECP；2(3)在点P运动过程中，假设1tan∠DCE＝，求AD的长．2【思路点拨】(1)利用同弧所对圆周角与圆心角之间的关系，可求得∠DOB＝60°，利用弧长公式求︵BD的长；先证得四边形DCPE是矩形，从而证明△DAC≌△ECP；(3)可以利用tan∠DCE在Rt△DAC中获得三边的数量关系，在Rt△AOC中建立方程求解．【自主解答】解：(1)∵∠ADC＝30°，OA＝OD，∴∠OAD＝30°.∴∠DOB＝60°.60×π×55π∴lBD＝180＝3.证明：连接OP.∵AO＝OP，点C是AP的中点，∴∠DCP＝90°.∵DE是⊙O的切线，∴∠CDE＝90°.∵AB是⊙O的直径，∴∠APB＝90°.∴四边形DCPE是矩形．∴DC＝EP.又∵AC＝CP，∠ACD＝∠CPE＝90°，∴△DAC≌△ECP( SAS)．由(2)知，四边形DCPE是矩形，△DAC≌△ECP，∴∠ADC＝∠CEP＝∠DCE.∵tan∠DCE＝1，∴tan∠ADC＝1.2∴设AC＝x，那么DC＝2x，AD＝5x.在Rt△AOC中，OC＝2x22－5，AO＝AC＋OC，2＋(2x 2∴5＝x－5)，解得x1＝0(舍去)，x2＝4.∴AD＝45 .【变式训练1】如图，AB是⊙O的直径，∠BAC＝60°，P是OB上一点，过点P作AB的垂线与AC的延长线交于点Q，过点C的切线CD交PQ于点D，连接OC.求证：△CDQ是等腰三角形；如果△CDQ≌△COB，求BP∶PO的值．解：(1)证明：∵AB是⊙O的直径，∴∠ACB＝90°.∵PQ⊥AB，∴∠APQ＝90°.又∵∠BAC＝60°，OA＝OC，∴△OAC是等边三角形，∠ABC＝∠Q＝30°.∴∠ACO＝60°.∴∠DCQ＝180°－90°－60°＝30°.∴∠DCQ＝∠Q.∴△CDQ是等腰三角形．3设⊙O的半径为x，那么AB＝2x，AC＝x，BC＝3x. ∵△CDQ≌△COB，∴CQ＝BC＝3x.11＋3∴AQ＝AC＋CQ＝(1＋3)x.∴AP＝2AQ＝2.3－33－1.∴BP＝AB－AP ＝x，PO＝AP－AO＝22∴BP∶PO＝ 3.方法指导1．遇切线，通常的方法是连接过切点的半径，利用切线垂直于过切点的半径，构建直角三角形，进而利用直角三角形进行求解或证明．2．在圆中还可以获得直角的方法有：平分弦(不是直径)的直径垂直于弦，直径所对的圆周角是直角．3．以圆为背景的求解题，往往转化成解双直角三角形或者相似三角形．Ｋ重难点2 切线的判定(2021·聊城)如图，在Rt△ABC中，∠C＝90°，BE平分∠ABC交AC于点E，作ED⊥EB交AB于点D，⊙O是△BED的外接圆．求证：AC是⊙O的切线；⊙O的半径为，BE＝4，求BC，AD的长．【思路点拨】(1)证AC是⊙O的切线，可转化为证OE⊥AC；(2)求BC，AD的长可通过证明△BDE∽△BEC和△AOE∽△ABC.【自主解答】解：(1)证明：连接OE.∵OB＝OE，∴∠OBE＝∠OEB.∵BE平分∠ABC，∴∠OBE＝∠CBE.∴∠OEB＝∠CBE.∴OE∥BC.又∵∠C＝90°，∴∠AEO＝90°，即OE⊥AC.又∵OE是⊙O的半径，∴AC为⊙O的切线．∵ED⊥BE，∴∠BED＝∠C＝90°.又∵∠DBE＝∠EBC，∴△BDE∽△BEC.B D BE5416，即.∴BC ＝.B E BC4BC5∵∠AEO＝∠C＝90°，∠A＝∠A，∴△AOE∽△ABC.A O OEAD＋45，即AD＋5＝.∴AD＝.A B BC 167 5【变式训练2】(2021·安顺)如图，在△ABC中，AB＝AC，点O为BC的中点，AC与半圆O 相切于点D.求证：AB是半圆O所在圆的切线；2(2)假设cos∠ABC＝3，AB＝12，求半圆O所在圆的半径．4解：(1)证明：作OE⊥AB于点E，连接OD，OA.∵AB＝AC，点O是BC的中点，∴∠CAO＝∠BAO.∵AC与半圆O相切于点D，∴OD⊥AC.又∵OE⊥AB，∴OD＝OE，即OE是半圆O所在圆的半径．∴AB是半圆O所在圆的切线．(2)∵AB＝AC，点O是BC的中点，∴AO⊥BC.2在Rt△AOB中，OB＝AB·cos∠ABC＝12×3＝8.根据勾股定理，得OA＝22AB－OB＝45.∵S ＝112AB·OE＝2OB·OA，△AOBOB·OA8585∴O E＝AB＝3，即半圆O所在圆的半径为3.方法指导1．证明某条直线是圆的切线的方法：假设这条直线经过圆上一点，需证明这条直线和经过这一点的半径垂直；假设没有明确直线经过圆上一点，需证明圆心到这条直线的距离等于圆的半径．2．不能或不易直接求解的边长可转化成易求两条边长的差或和．重难点3 三角形的内心与外心如图，点O为锐角△ABC的外心，四边形 OCDE为正方形，其中E点在△ABC的外部，判断以下说法正确的是(B)A．点O是△AEB的外心，点O是△AED的外心B．点O是△AEB的外心，点O不是△AED的外心C．点O不是△AEB的外心，点O是△AED的外心D．点O不是△AEB的外心，点O不是△AED的外心【变式训练3】如图，假设点O是AB的中点，且点O不是一个三角形的外心，那么这个三角形可以是(B)A．△ABC B．△ABE C．△ABF D．△ABD5【变式训练4】如图，⊙O截△ABC的三条边所得的弦长相等，那么以下说法正确的选项是(A)A．点O是△ABC的内心B．点O是△ABC的外心C．△ABC是正三角形D．△ABC是等腰三角形【变式训练5】如图，△ABC的外心坐标是(B)A．(－1，－2) B．(－2，－1) C．(－2，－2) D．(－1，－1)方法指导1．判断点是某个三角形的外心，只需说明点到此三角形的三个顶点的距离相等即可；判断点是某个三角形的内心，只需说明点到此三角形三边的距离相等即可．2．三角形的内心是三角形角平分线的交点，又是三角形内切圆的圆心；三角形的外心是三角形各边垂直平分线的交点，又是三角形外接圆的圆心．它是串联圆与三角形之间的关键点，可以利用它从一个图形过渡到另一个图形．重难点4 切线长定理如图，△ABC是一张周长为17cm的三角形纸片，BC＝5cm，⊙O是它的内切圆，小明准备用剪刀在⊙O 的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN，那么剪下的三角形的周长为(B)A．12cm B ．7cm C ．6cm D ．随直线MN的变化而变化【思路点拨】由切线长定理，可将△AMN的周长转化成求AD＋AE的和，而BD＋CE的和等于BC.【变式训练6】如图，EB，EC是⊙O的两条切线，B，C是切点，A，D是⊙O上两点．假设∠E＝46°，∠DCF＝32°，6那么∠A的度数是99°．方法指导1．由切线长定理及三角形周长可得：1①AD＝2C△ABC－BC；1②BD＝2C△ABC－AC；1③CE＝2C△ABC－AB.2．假设三角形的内切圆及切点，求线段的长或周长时，往往用到切线长定理．1．⊙O的半径为6，圆心O到直线l的距离为10，那么反映直线l与⊙O的位置关系的图形是(D)2．⊙O的半径是3，点P在圆内，那么线段OP的长可能是()A．2B．3C．4D．53．(2021·宜昌)如图，直线AB是⊙O的切线，C为切点，OD∥AB交⊙O于点D，点E在⊙O上，连接OC，EC，ED，那么∠CED的度数为(D)A．30°B．35°C．40°D．45°4．(2021·河北模拟)九个相同的等边三角形如下图，点O是一个三角形的外心，那么这个三角形是(C)A．△ABC B．△ABE C．△ABD D．△ACE5．(2021·保定模拟)如图，在△ABC中，AB＝3，AC＝4，BC＝5，点D，E分别是AC，AB的中点，那么以DE为直径的圆与BC的位置关系是(B)A．相切B．相交C．相离D．无法确定76．(2021·烟台)如图，四边形ABCD内接于⊙O，点I是△ABC的内心，∠AIC＝124°，点E在AD的延长线上，那么∠CDE的度数为(C)A．56° B．62° C．68° D．78°7．(2021·石家庄长安区模拟)如图，网格中的每个小正方形的边长都是 1，点M，N，O均为格点，点N在⊙O上．假设过点M作⊙O的一条切线MK，切点为K，那么MK＝(B)A．3 2 B．2 5 C．5 D. 348．(2021·烟台)如图，方格纸上每个小正方形的边长均为 1个单位长度，点O，A，B，C在格点(两条网格线的交点叫格点)上，以点O为原点建立平面直角坐标系，那么过 A，B，C三点的圆的圆心坐标为(－1，－2)．9．(2021·安徽)如图，菱形ABOC的边AB，AC分别与⊙O相切于点 D，E.假设点D是AB的中点，那么∠DOE＝60°．10．(2021·邵阳)如下图，AB是⊙O的直径，点C为⊙O上一点，过点B作BD⊥CD，垂足为D，连接BC，BC平分∠ABD.求证：CD为⊙O的切线．8证明：∵BC平分∠ABD，∴∠OBC＝∠DBC.∵OB＝OC，∴∠OBC＝∠OCB.∴∠OCB＝∠DBC.∴OC∥BD.∵BD⊥CD，∴OC⊥CD.又∵OC为⊙O的半径，∴CD为⊙O的切线．11．(2021·黄冈)如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的切线交OP于点C.(1)求证：∠CBP＝∠D；(2)假设OA＝2，AB＝1，求线段BP的长．解：(1)证明：连接OB.∵AD是⊙O的直径，∴∠ABD＝90°.∴∠A＋∠D＝90°.∵BC为切线，∴OB⊥BC，即∠OBC＝90°.∴∠OBA＋∠CBP＝90°.∵OA＝OB，∴∠A＝∠OBA.∴∠CBP＝∠D.∵OP⊥AD，∴∠POA＝90°.∴∠P＋∠A＝90°.∴∠P＝∠D.又∵∠A＝∠A，∴△AOP∽△ABD.A PAO1＋BP2∴＝，即4＝.A DAB1∴BP＝7.12．(2021·荆门)如图，在平面直角坐标系xOy中，A(4，0)，B(0，3)，C(4，3)，I是△ABC的内心，将△ABC绕原点O逆时针旋转90°后，I的对应点I′的坐标为(A)A．(－2，3) B．(－3，2) C．(3，－2) D．(2，－3)提示：I(3，2)．913．(2021·台州)如图，等边三角形ABC边长是定值，点O是它的外心，过点O任意作一条直线分别交AB，BC于点D，E.将△BDE沿直线DE折叠，得到△B′DE，假设B′D，B′E分别交AC于点F，G，连接OF，OG，那么以下判断错误的选项是(D)A．△ADF≌△CG EB．△B′FG的周长是一个定值C．四边形FOEC 的面积是一个定值D．四边形OGB′F的面积是一个定值提示：连接OA，OC，易证△DOF≌△GOF≌△GO E，△OAD≌△OCG，△OAF≌△OCE，△ADF≌△CGE，应选项A正确；∵△DOF≌△GOF≌△GOE，∴DF＝GF＝GE.∴△ADF≌△B′GF≌△CGE∴.B′F＝AF，B′G＝CG.∴C△B′FG＝FG＋B′F1＋B′G＝FG＋AF＋CG＝AC(定值)，应选项B正确；S四边形FOEC＝S△OCF＋S△OCE＝S△OCF＋S△OAF＝S△AOC＝3S△ABC(定值)，应选项C正确；S四边形OGB＝SOFG＋SBGF＝SOFD＋SADF＝S＝S＋S＝S＋S＝S－S，过点O作OH⊥AC′F△△′△四边形OFAD△OAD△OAF△OCG△OAF△OAC△OFG于点H，∴S1OGB′F的面积也变化，故＝2FG·OH，由于OH是定值，FG变化，故△OFG的面积变化，从而四边形△OFG选项D错误．14．(2021·南京)如图，在矩形ABCD中，AB＝5，BC＝4，以CD为直径作⊙O.将矩形ABCD绕点C旋转，使所得矩形A′B′CD′的边A′B′与⊙O相切，切点为E，边CD′与⊙O相交于点F，那么CF的长为4．提示：连接22OE，延长EO交CD′于点G，那么OE＝OC＝2.5.∴OG＝EG－OE＝1.5.∴CG＝OC－OG＝2.∴CF ＝2CG＝4.15．【分类讨论思想】(2021·宁波)如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连接PM，以点P为圆心，PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时，BP的长为3或43．1提示：分两种情况讨论：①当⊙P与直线CD相切时，BP＝3；②当⊙P与直线AD相切时，PB＝4 3.16．(2021·扬州)如图，在△ABC中，AB＝AC，AO⊥BC于点O，OE⊥AB于点E，以点O为圆心，OE为半径作半圆，交AO于点F.求证：AC是⊙O的切线；假设点F是OA的中点，OE＝3，求图中阴影局部的面积；(3)在(2)的条件下，点P是BC边上的动点，当PE＋PF取最小值时，直接写出BP的长．解：(1)证明：作OH⊥AC于点H.∵AB＝AC，AO⊥BC，∴AO平分∠BAC.又∵OE⊥AB，OH⊥AC，∴OH＝OE，即OH为⊙O的半径．∴AC是⊙O的切线．∵点F是OA的中点，∴OA＝2OF＝2OE＝6.又∵OE＝3，∴∠OAE＝30°，∠AOE＝60°.∴AE＝3 3.∴S阴影＝S△AOE－S扇形EOF12 60×π×3＝2×3×33－360＝93－3π.2作F点关于BC的对称点F′，连接EF′交BC于点P，此时PE＋PF最小．∵OF′＝OF＝OE，∴∠F′＝∠OEF′.∵∠AOE＝∠F′＋∠OEF′＝60°，∴∠F′＝30°.∴∠F′＝∠EAF′.EF′＝EA＝33，即PE＋PF最小值为33.在Rt△OPF′中，OP＝tan30°·OF′＝3，在Rt△ABO中，OB＝tan30°·OA＝23，∴BP＝23－3＝3.11。

2019年河北省中考数学试题及参考答案与解析（总分120分，考试时间120分钟）卷Ⅰ（选择题，共42分）一、选择题（本大题有16个小题，共42分，1-10小题各3分，11-16小题各2分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．下列图形为正多边形的是（）A．B．C．D．2．规定：（→2）表示向右移动2记作+2，则（←3）表示向左移动3记作（）A．+3 B．﹣3 C．﹣D．+3．如图，从点C观测点D的仰角是（）A．∠DAB B．∠DCE C．∠DCA D．∠ADC4．语句“x的与x的和不超过5”可以表示为（）A．+x≤5 B．+x≥5 C．≤5 D．+x＝55．如图，菱形ABCD中，∠D＝150°，则∠1＝（）A．30°B．25°C．20°D．15°6．小明总结了以下结论：①a（b+c）＝ab+ac；②a（b﹣c）＝ab﹣ac；③（b﹣c）÷a＝b÷a﹣c÷a（a≠0）；④a÷（b+c）＝a÷b+a÷c（a≠0）其中一定成立的个数是（）A．1 B．2 C．3 D．47．下面是投影屏上出示的抢答题，需要回答横线上符号代表的内容则回答正确的是（）A．◎代表∠FEC B．@代表同位角C．▲代表∠EFC D．※代表AB8．一次抽奖活动特等奖的中奖率为，把用科学记数法表示为（）A．5×10﹣4B．5×10﹣5C．2×10﹣4D．2×10﹣59．如图，在小正三角形组成的网格中，已有6个小正三角形涂黑，还需涂黑n 个小正三角形，使它们与原来涂黑的小正三角形组成的新图案恰有三条对称轴，则n的最小值为（）A．10 B．6 C．3 D．210．根据圆规作图的痕迹，可用直尺成功找到三角形外心的是（）A．B．C．D．11．某同学要统计本校图书馆最受学生欢迎的图书种类，以下是排乱的统计步骤：①从扇形图中分析出最受学生欢迎的种类②去图书馆收集学生借阅图书的记录③绘制扇形图来表示各个种类所占的百分比④整理借阅图书记录并绘制频数分布表正确统计步骤的顺序是（）A．②→③→①→④B．③→④→①→②C．①→②一④→③D．②→④→③→①12．如图，函数y＝的图象所在坐标系的原点是（）A．点M B．点N C．点P D．点Q13．如图，若x为正整数，则表示﹣的值的点落在（）A．段①B．段②C．段③D．段④14．图2是图1中长方体的三视图，若用S表示面积，S主＝x2+2x，S左＝x2+x，则S俯＝（）A．x2+3x+2 B．x2+2 C．x2+2x+1 D．2x2+3x15．小刚在解关于x的方程ax2+bx+c＝0（a≠0）时，只抄对了a＝1，b＝4，解出其中一个根是x ＝﹣1．他核对时发现所抄的c比原方程的c值小2．则原方程的根的情况是（）A．不存在实数根B．有两个不相等的实数根C．有一个根是x＝﹣1 D．有两个相等的实数根16．对于题目：“如图1，平面上，正方形内有一长为12、宽为6的矩形，它可以在正方形的内部及边界通过移转（即平移或旋转）的方式，自由地从横放移转到竖放，求正方形边长的最小整数n．”甲、乙、丙作了自认为边长最小的正方形，先求出该边长x，再取最小整数n．甲：如图2，思路是当x为矩形对角线长时就可移转过去；结果取n＝13．乙：如图3，思路是当x为矩形外接圆直径长时就可移转过去；结果取n＝14．丙：如图4，思路是当x为矩形的长与宽之和的倍时就可移转过去；结果取n＝13．下列正确的是（）A．甲的思路错，他的n值对B．乙的思路和他的n值都对C．甲和丙的n值都对D．甲、乙的思路都错，而丙的思路对卷Ⅱ（非选择题，共78分）二、填空题（本大题有3个小题，共11分，17小题3分，18～19小题各有2个空，每空2分）17．若7﹣2×7﹣1×70＝7p，则p的值为．18．如图，约定：上方相邻两数之和等于这两数下方箭头共同指向的数．示例：即4+3＝7则（1）用含x的式子表示m＝；（2）当y＝﹣2时，n的值为．19．勘测队按实际需要构建了平面直角坐标系，并标示了A，B，C三地的坐标，数据如图（单位：km）．笔直铁路经过A，B两地．（1）A，B间的距离为km；（2）计划修一条从C到铁路AB的最短公路l，并在l上建一个维修站D，使D到A，C的距离相等，则C，D间的距离为km．三、解答题（本大题有7个小题，共67分.解答应写出文字说明、证明过程或演算步骤）20．（8分）有个填写运算符号的游戏：在“1□2□6□9”中的每个□内，填入+，﹣，×，÷中的某一个（可重复使用），然后计算结果．（1）计算：1+2﹣6﹣9；（2）若1÷2×6□9＝﹣6，请推算□内的符号；（3）在“1□2□6﹣9”的□内填入符号后，使计算所得数最小，直接写出这个最小数．21．（9分）已知：整式A＝（n2﹣1）2+（2n）2，整式B＞0．尝试化简整式A．发现A＝B2，求整式B．联想由上可知，B2＝（n2﹣1）2+（2n）2，当n＞1时，n2﹣1，2n，B为直角三角形的三边长，如图．填写下表中B的值：直角三角形三边n2﹣1 2n B勾股数组Ⅰ/ 8勾股数组Ⅱ35 /22．（9分）某球室有三种品牌的4个乒乓球，价格是7，8，9（单位：元）三种．从中随机拿出一个球，已知P（一次拿到8元球）＝．（1）求这4个球价格的众数；（2）若甲组已拿走一个7元球训练，乙组准备从剩余3个球中随机拿一个训练．①所剩的3个球价格的中位数与原来4个球价格的中位数是否相同？并简要说明理由；②乙组先随机拿出一个球后放回，之后又随机拿一个，用列表法（如图）求乙组两次都拿到8元球的概率．又拿先拿23．（9分）如图，△ABC和△ADE中，AB＝AD＝6，BC＝DE，∠B＝∠D＝30°，边AD与边BC 交于点P（不与点B，C重合），点B，E在AD异侧，I为△APC的内心．（1）求证：∠BAD＝∠CAE；（2）设AP＝x，请用含x的式子表示PD，并求PD的最大值；（3）当AB⊥AC时，∠AIC的取值范围为m°＜∠AIC＜n°，分别直接写出m，n的值．24．（10分）长为300m的春游队伍，以v（m/s）的速度向东行进，如图1和图2，当队伍排尾行进到位置O时，在排尾处的甲有一物品要送到排头，送到后立即返回排尾，甲的往返速度均为2v （m/s），当甲返回排尾后，他及队伍均停止行进．设排尾从位置O开始行进的时间为t（s），排头与O的距离为S头（m）．（1）当v＝2时，解答：①求S头与t的函数关系式（不写t的取值范围）；②当甲赶到排头位置时，求S头的值；在甲从排头返回到排尾过程中，设甲与位置O的距离为S甲（m），求S甲与t的函数关系式（不写t的取值范围）（2）设甲这次往返队伍的总时间为T（s），求T与v的函数关系式（不写v的取值范围），并写出队伍在此过程中行进的路程．25．（10分）如图1和2，▱ABCD中，AB＝3，BC＝15，tan∠DAB＝．点P为AB延长线上一点，过点A作⊙O切CP于点P，设BP＝x．（1）如图1，x为何值时，圆心O落在AP上？若此时⊙O交AD于点E，直接指出PE与BC的位置关系；（2）当x＝4时，如图2，⊙O与AC交于点Q，求∠CAP的度数，并通过计算比较弦AP与劣弧长度的大小；（3）当⊙O与线段AD只有一个公共点时，直接写出x的取值范围．26．（12分）如图，若b是正数，直线l：y＝b与y轴交于点A；直线a：y＝x﹣b与y轴交于点B；抛物线L：y＝﹣x2+bx的顶点为C，且L与x轴右交点为D．（1）若AB＝8，求b的值，并求此时L的对称轴与a的交点坐标；（2）当点C在l下方时，求点C与l距离的最大值；（3）设x0≠0，点（x0，y1），（x0，y2），（x0，y3）分别在l，a和L上，且y3是y1，y2的平均数，求点（x0，0）与点D间的距离；（4）在L和a所围成的封闭图形的边界上，把横、纵坐标都是整数的点称为“美点”，分别直接写出b＝2019和b＝2019.5时“美点”的个数．参考答案与解析卷Ⅰ（选择题，共42分）一、选择题（本大题有16个小题，共42分，1-10小题各3分，11-16小题各2分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．下列图形为正多边形的是（）A．B．C．D．【知识考点】多边形．【思路分析】根据正多边形的定义；各个角都相等，各条边都相等的多边形叫做正多边形可得答案．【解答过程】解：正五边形五个角相等，五条边都相等，故选：D．【总结归纳】此题主要考查了正多边形，关键是掌握正多边形的定义．2．规定：（→2）表示向右移动2记作+2，则（←3）表示向左移动3记作（）A．+3 B．﹣3 C．﹣D．+【知识考点】正数和负数．【思路分析】在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．“正”和“负”相对，所以，如果（→2）表示向右移动2记作+2，则（←3）表示向左移动3记作﹣3．【解答过程】解：“正”和“负”相对，所以，如果（→2）表示向右移动2记作+2，则（←3）表示向左移动3记作﹣3．故选：B．【总结归纳】此题考查了正数和负数，解题关键是理解“正”和“负”的相对性，确定一对具有相反意义的量．3．如图，从点C观测点D的仰角是（）A．∠DAB B．∠DCE C．∠DCA D．∠ADC【知识考点】解直角三角形的应用﹣仰角俯角问题．【思路分析】根据仰角的定义进行解答便可．【解答过程】解：∵从点C观测点D的视线是CD，水平线是CE，∴从点C观测点D的仰角是∠DCE，故选：B．【总结归纳】本题主要考查了仰角的识别，熟记仰角的定义是解题的关键．仰角是向上看的视线与水平线的夹角；俯角是向下看的视线与水平线的夹角．4．语句“x的与x的和不超过5”可以表示为（）A．+x≤5 B．+x≥5 C．≤5 D．+x＝5【知识考点】由实际问题抽象出一元一次不等式．【思路分析】x的即x，不超过5是小于或等于5的数，按语言叙述列出式子即可．【解答过程】解：“x的与x的和不超过5”用不等式表示为x+x≤5．故选：A．【总结归纳】本题考查了由实际问题抽象出一元一次不等式，读懂题意，抓住关键词语，弄清运算的先后顺序和不等关系，才能把文字语言的不等关系转化为用数学符号表示的不等式．5．如图，菱形ABCD中，∠D＝150°，则∠1＝（）A．30°B．25°C．20°D．15°【知识考点】菱形的性质．【思路分析】由菱形的性质得出AB∥CD，∠BAD＝2∠1，求出∠BAD＝30°，即可得出∠1＝15°．【解答过程】解：∵四边形ABCD是菱形，∠D＝150°，∴AB∥CD，∠BAD＝2∠1，∴∠BAD+∠D＝180°，∴∠BAD＝180°﹣150°＝30°，∴∠1＝15°；故选：D．【总结归纳】此题考查了菱形的性质，以及平行线的性质，熟练掌握菱形的性质是解本题的关键．6．小明总结了以下结论：①a（b+c）＝ab+ac；②a（b﹣c）＝ab﹣ac；③（b﹣c）÷a＝b÷a﹣c÷a（a≠0）；④a÷（b+c）＝a÷b+a÷c（a≠0）其中一定成立的个数是（）A．1 B．2 C．3 D．4【知识考点】单项式乘多项式．【思路分析】直接利用单项式乘以多项式以及多项式除以单项式运算法则计算得出答案．【解答过程】解：①a（b+c）＝ab+ac，正确；②a（b﹣c）＝ab﹣ac，正确；③（b﹣c）÷a＝b÷a﹣c÷a（a≠0），正确；④a÷（b+c）＝a÷b+a÷c（a≠0），错误，无法分解计算．故选：C．【总结归纳】此题主要考查了单项式乘以多项式以及多项式除以单项式运算，正确掌握相关运算法则是解题关键．7．下面是投影屏上出示的抢答题，需要回答横线上符号代表的内容则回答正确的是（）A．◎代表∠FEC B．@代表同位角C．▲代表∠EFC D．※代表AB【知识考点】平行线的判定．【思路分析】根据图形可知※代表CD，即可判断D；根据三角形外角的性质可得◎代表∠EFC，即可判断A；利用等量代换得出▲代表∠EFC，即可判断C；根据图形已经内错角定义可知@代表内错角．【解答过程】证明：延长BE交CD于点F，则∠BEC＝∠EFC+∠C（三角形的外角等于与它不相邻两个内角之和）．又∠BEC＝∠B+∠C，得∠B＝∠EFC．故AB∥CD（内错角相等，两直线平行）．故选：C．【总结归纳】本题考查了平行线的判定，三角形外角的性质，比较简单．8．一次抽奖活动特等奖的中奖率为，把用科学记数法表示为（）A．5×10﹣4B．5×10﹣5C．2×10﹣4D．2×10﹣5【知识考点】科学记数法—表示较小的数．【思路分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【解答过程】解：＝0.00002＝2×10﹣5．故选：D．【总结归纳】本题考查用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．9．如图，在小正三角形组成的网格中，已有6个小正三角形涂黑，还需涂黑n个小正三角形，使它们与原来涂黑的小正三角形组成的新图案恰有三条对称轴，则n的最小值为（）A．10 B．6 C．3 D．2【知识考点】利用轴对称设计图案．【思路分析】由等边三角形有三条对称轴可得答案．【解答过程】解：如图所示，n的最小值为3，故选：C．【总结归纳】本题主要考查利用轴对称设计图案，解题的关键是掌握常见图形的性质和轴对称图形的性质．10．根据圆规作图的痕迹，可用直尺成功找到三角形外心的是（）A．B．C．D．【知识考点】三角形的外接圆与外心；作图—基本作图．【思路分析】根据三角形外心的定义，三角形外心为三边的垂直平分线的交点，然后利用基本作图格选项进行判断．【解答过程】解：三角形外心为三边的垂直平分线的交点，由基本作图得到C选项作了两边的垂直平分线，从而可用直尺成功找到三角形外心．故选：C．【总结归纳】本题考查了作图﹣基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．也考查了三角形的外心．11．某同学要统计本校图书馆最受学生欢迎的图书种类，以下是排乱的统计步骤：①从扇形图中分析出最受学生欢迎的种类②去图书馆收集学生借阅图书的记录③绘制扇形图来表示各个种类所占的百分比④整理借阅图书记录并绘制频数分布表正确统计步骤的顺序是（）A．②→③→①→④B．③→④→①→②C．①→②一④→③D．②→④→③→①【知识考点】调查收集数据的过程与方法；频数（率）分布表；扇形统计图．【思路分析】根据题意和频数分布表、扇形统计图制作的步骤，可以解答本题．【解答过程】解：由题意可得，正确统计步骤的顺序是：②去图书馆收集学生借阅图书的记录→④整理借阅图书记录并绘制频数分布表→③绘制扇形图来表示各个种类所占的百分比→①从扇形图中分析出最受学生欢迎的种类，故选：D．【总结归纳】本题考查扇形统计图、频数分布表，解答本题的关键是明确制作频数分布表和扇形统计图的制作步骤．12．如图，函数y＝的图象所在坐标系的原点是（）A．点M B．点N C．点P D．点Q【知识考点】反比例函数的图象．【思路分析】由函数解析式可知函数关于y轴对称，即可求解；【解答过程】解：由已知可知函数y＝关于y轴对称，所以点M是原点；故选：A．【总结归纳】本题考查反比例函数的图象及性质；熟练掌握函数的解析式与函数图象的关系是解题的关键．13．如图，若x为正整数，则表示﹣的值的点落在（）A．段①B．段②C．段③D．段④【知识考点】分式的加减法．【思路分析】将所给分式的分母配方化简，再利用分式加减法化简，根据x为正整数，从所给图中可得正确答案．【解答过程】解∵﹣＝﹣＝1﹣＝又∵x为正整数，∴≤x＜1故表示﹣的值的点落在②故选：B．【总结归纳】本题考查了分式的化简及分式加减运算，同时考查了分式值的估算，总体难度中等．14．图2是图1中长方体的三视图，若用S表示面积，S主＝x2+2x，S左＝x2+x，则S俯＝（）A．x2+3x+2 B．x2+2 C．x2+2x+1 D．2x2+3x【知识考点】几何体的表面积；由三视图判断几何体．【思路分析】由主视图和左视图的宽为x，结合两者的面积得出俯视图的长和宽，从而得出答案．【解答过程】解：∵S主＝x2+2x＝x（x+2），S左＝x2+x＝x（x+1），∴俯视图的长为x+2，宽为x+1，则俯视图的面积S俯＝（x+2）（x+1）＝x2+3x+2，故选：A．【总结归纳】本题主要考查由三视图判断几何体，解题的关键是根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，以及几何体的长、宽、高．15．小刚在解关于x的方程ax2+bx+c＝0（a≠0）时，只抄对了a＝1，b＝4，解出其中一个根是x ＝﹣1．他核对时发现所抄的c比原方程的c值小2．则原方程的根的情况是（）A．不存在实数根B．有两个不相等的实数根C．有一个根是x＝﹣1 D．有两个相等的实数根【知识考点】解一元二次方程﹣公式法；根的判别式．【思路分析】直接把已知数据代入进而得出c的值，再解方程求出答案．【解答过程】解：∵小刚在解关于x的方程ax2+bx+c＝0（a≠0）时，只抄对了a＝1，b＝4，解出其中一个根是x＝﹣1，∴（﹣1）2﹣4+c＝0，解得：c＝3，故原方程中c＝5，则b2﹣4ac＝16﹣4×1×5＝﹣4＜0，则原方程的根的情况是不存在实数根．故选：A．【总结归纳】此题主要考查了根的判别式，正确得出c的值是解题关键．16．对于题目：“如图1，平面上，正方形内有一长为12、宽为6的矩形，它可以在正方形的内部及边界通过移转（即平移或旋转）的方式，自由地从横放移转到竖放，求正方形边长的最小整数n．”甲、乙、丙作了自认为边长最小的正方形，先求出该边长x，再取最小整数n．甲：如图2，思路是当x为矩形对角线长时就可移转过去；结果取n＝13．乙：如图3，思路是当x为矩形外接圆直径长时就可移转过去；结果取n＝14．丙：如图4，思路是当x为矩形的长与宽之和的倍时就可移转过去；结果取n＝13．下列正确的是（）A．甲的思路错，他的n值对B．乙的思路和他的n值都对C．甲和丙的n值都对D．甲、乙的思路都错，而丙的思路对【知识考点】矩形的性质；正方形的性质；平移的性质；旋转的性质．【思路分析】平行四边形的性质矩形都具有；②角：矩形的四个角都是直角；③边：邻边垂直；④对角线：矩形的对角线相等；⑤矩形是轴对称图形，又是中心对称图形．它有2条对称轴，分别是每组对边中点连线所在的直线；对称中心是两条对角线的交点．【解答过程】解：甲的思路正确，长方形对角线最长，只要对角线能通过就可以，但是计算错误，应为n＝14；乙的思路与计算都正确；乙的思路与计算都错误，图示情况不是最长；故选：B．【总结归纳】本题考查了矩形的性质与旋转的性质，熟练运用矩形的性质是解题的关键．卷Ⅱ（非选择题，共78分）二、填空题（本大题有3个小题，共11分，17小题3分，18～19小题各有2个空，每空2分）17．若7﹣2×7﹣1×70＝7p，则p的值为．【知识考点】零指数幂；负整数指数幂．【思路分析】直接利用同底数幂的乘法运算法则进而得出答案．【解答过程】解：∵7﹣2×7﹣1×70＝7p，∴﹣2﹣1+0＝p，解得：p＝﹣3．故答案为：﹣3．【总结归纳】此题主要考查了同底数幂的乘法运算，正确掌握相关运算法则是解题关键．18．如图，约定：上方相邻两数之和等于这两数下方箭头共同指向的数．示例：即4+3＝7则（1）用含x的式子表示m＝；（2）当y＝﹣2时，n的值为．【知识考点】列代数式；代数式求值．【思路分析】（1）根据约定的方法即可求出m；（2）根据约定的方法即可求出n．【解答过程】解：（1）根据约定的方法可得：m＝x+2x＝3x；故答案为：3x；（2）根据约定的方法即可求出nx+2x+2x+3＝m+n＝y．当y＝﹣2时，5x+3＝﹣2．解得x＝﹣1．∴n＝2x+3＝﹣2+3＝1．故答案为：1．【总结归纳】本题考查了列代数式和代数式求值，解题的关键是掌握列代数式的约定方法．19．勘测队按实际需要构建了平面直角坐标系，并标示了A，B，C三地的坐标，数据如图（单位：km）．笔直铁路经过A，B两地．（1）A，B间的距离为km；（2）计划修一条从C到铁路AB的最短公路l，并在l上建一个维修站D，使D到A，C的距离相等，则C，D间的距离为km．【知识考点】勾股定理的应用．【思路分析】（1）由垂线段最短以及根据两点的纵坐标相同即可求出AB的长度；（2）根据A、B、C三点的坐标可求出CE与AE的长度，设CD＝x，根据勾股定理即可求出x 的值．【解答过程】解：（1）由A、B两点的纵坐标相同可知：AB∥x轴，∴AB＝12﹣（﹣8）20；（2）过点C作l⊥AB于点E，连接AC，作AC的垂直平分线交直线l于点D，由（1）可知：CE＝1﹣（﹣17）＝18，AE＝12，设CD＝x，∴AD＝CD＝x，由勾股定理可知：x2＝（18﹣x）2+122，∴解得：x＝13，∴CD＝13，故答案为：（1）20；（2）13；【总结归纳】本题考查勾股定理，解题的关键是根据A、B、C三点的坐标求出相关线段的长度，本题属于中等题型．三、解答题（本大题有7个小题，共67分.解答应写出文字说明、证明过程或演算步骤）20．（8分）有个填写运算符号的游戏：在“1□2□6□9”中的每个□内，填入+，﹣，×，÷中的某一个（可重复使用），然后计算结果．（1）计算：1+2﹣6﹣9；（2）若1÷2×6□9＝﹣6，请推算□内的符号；（3）在“1□2□6﹣9”的□内填入符号后，使计算所得数最小，直接写出这个最小数．【知识考点】有理数的混合运算．【思路分析】（1）根据有理数的加减法可以解答本题；（2）根据题目中式子的结果，可以得到□内的符号；（3）先写出结果，然后说明理由即可．【解答过程】解：（1）1+2﹣6﹣9＝3﹣6﹣9＝﹣3﹣9＝﹣12；（2）∵1÷2×6□9＝﹣6，∴1××6□9＝﹣6，∴3□9＝﹣6，∴□内的符号是“﹣”；（3）这个最小数是﹣20，理由：∵在“1□2□6﹣9”的□内填入符号后，使计算所得数最小，∴1□2□6的结果是负数即可，∴1□2□6的最小值是1﹣2×6＝﹣11，∴1□2□6﹣9的最小值是﹣11﹣9＝﹣20，∴这个最小数是﹣20．【总结归纳】本题考查有理数的混合运算，解答本题得关键是明确有理数混合运算的计算方法．21．（9分）已知：整式A＝（n2﹣1）2+（2n）2，整式B＞0．尝试化简整式A．发现A＝B2，求整式B．联想由上可知，B2＝（n2﹣1）2+（2n）2，当n＞1时，n2﹣1，2n，B为直角三角形的三边长，如图．填写下表中B的值：直角三角形三边n2﹣1 2n B勾股数组Ⅰ/ 8 15勾股数组Ⅱ35 / 37【知识考点】幂的乘方与积的乘方；勾股数．【思路分析】先根据整式的混合运算法则求出A，进而求出B，再把n的值代入即可解答．【解答过程】解：A＝（n2﹣1）2+（2n）2＝n4﹣2n2+1+4n2＝n4+2n2+1＝（n2+1）2，∵A＝B2，B＞0，∴B＝n2+1，当2n＝8时，n＝4，∴n2+1＝42+1＝15；当n2﹣1＝35时，n2+1＝37．故答案为：15；37【总结归纳】本题考查了勾股数的定义，及勾股定理的逆定理：已知△ABC的三边满足a2+b2＝c2，则△ABC是直角三角形．22．（9分）某球室有三种品牌的4个乒乓球，价格是7，8，9（单位：元）三种．从中随机拿出一个球，已知P（一次拿到8元球）＝．（1）求这4个球价格的众数；（2）若甲组已拿走一个7元球训练，乙组准备从剩余3个球中随机拿一个训练．①所剩的3个球价格的中位数与原来4个球价格的中位数是否相同？并简要说明理由；②乙组先随机拿出一个球后放回，之后又随机拿一个，用列表法（如图）求乙组两次都拿到8元球的概率．又拿先拿【知识考点】分式方程的应用；中位数；众数；概率公式；列表法与树状图法．【思路分析】（1）由概率公式求出8元球的个数，由众数的定义即可得出答案；（2）①由中位数的定义即可得出答案；②用列表法得出所有结果，乙组两次都拿到8元球的结果有4个，由概率公式即可得出答案．【解答过程】解：（1）∵P（一次拿到8元球）＝，∴8元球的个数为4×＝2（个），按照从小到大的顺序排列为7，8，8，9，∴这4个球价格的众数为8元；（2）①所剩的3个球价格的中位数与原来4个球价格的中位数相同；理由如下：原来4个球的价格按照从小到大的顺序排列为7，8，8，9，∴原来4个球价格的中位数为＝8（元），所剩的3个球价格为8，8，9，∴所剩的3个球价格的中位数为8元，∴所剩的3个球价格的中位数与原来4个球价格的中位数相同；②列表如图所示：共有9个等可能的结果，乙组两次都拿到8元球的结果有4个，∴乙组两次都拿到8元球的概率为．【总结归纳】本题考查了众数、中位数以及列表法求概率；熟练掌握众数、中位数的定义，列表得出所有结果是解题的关键．23．（9分）如图，△ABC和△ADE中，AB＝AD＝6，BC＝DE，∠B＝∠D＝30°，边AD与边BC 交于点P（不与点B，C重合），点B，E在AD异侧，I为△APC的内心．（1）求证：∠BAD＝∠CAE；（2）设AP＝x，请用含x的式子表示PD，并求PD的最大值；（3）当AB⊥AC时，∠AIC的取值范围为m°＜∠AIC＜n°，分别直接写出m，n的值．【知识考点】圆的综合题．【思路分析】（1）由条件易证△ABC≌△ADE，得∠BAC＝∠DAE，∴∠BAD＝∠CAE．（2）PD＝AD﹣AP＝6﹣x，∵点P在线段BC上且不与B、C重合，∴AP的最小值即AP⊥BC 时AP的长度，此时PD可得最大值．（3）I为△APC的内心，即I为△APC角平分线的交点，应用“三角形内角和等于180°“及角平分线定义即可表示出∠AIC，从而得到m，n的值．【解答过程】解：（1）在△ABC和△ADE中，（如图1）∴△ABC≌△ADE（SAS）∴∠BAC＝∠DAE即∠BAD+∠DAC＝∠DAC+∠CAE∴∠BAD＝∠CAE．（2）∵AD＝6，AP＝x，∴PD＝6﹣x当AD⊥BC时，AP＝AB＝3最小，即PD＝6﹣3＝3为PD的最大值．（3）如图2，设∠BAP＝α，则∠APC＝α+30°，∵AB⊥AC∴∠BAC＝90°，∠PCA＝60°，∠PAC＝90°﹣α，∵I为△APC的内心∴AI、CI分别平分∠PAC，∠PCA，∴∠IAC＝∠PAC，∠ICA＝∠PCA∴∠AIC＝180°﹣（∠IAC+∠ICA）＝180°﹣（∠PAC+∠PCA）＝180°﹣（90°﹣α+60°）＝α+105°∵0＜α＜90°，∴105°＜α+105°＜150°，即105°＜∠AIC＜150°，∴m＝105，n＝150．【总结归纳】本题是一道几何综合题，考查了点到直线的距离垂线段最短，30°的角所对的直角边等于斜边的一半，全等三角形的判定和性质，三角形内心概念及角平分线定义等，解题关键是将PD最大值转化为PA的最小值．24．（10分）长为300m的春游队伍，以v（m/s）的速度向东行进，如图1和图2，当队伍排尾行进到位置O时，在排尾处的甲有一物品要送到排头，送到后立即返回排尾，甲的往返速度均为2v （m/s），当甲返回排尾后，他及队伍均停止行进．设排尾从位置O开始行进的时间为t（s），排头与O的距离为S头（m）．（1）当v＝2时，解答：①求S头与t的函数关系式（不写t的取值范围）；②当甲赶到排头位置时，求S头的值；在甲从排头返回到排尾过程中，设甲与位置O的距离为S甲（m），求S甲与t的函数关系式（不写t的取值范围）（2）设甲这次往返队伍的总时间为T（s），求T与v的函数关系式（不写v的取值范围），并写出队伍在此过程中行进的路程．【知识考点】反比例函数的应用．【思路分析】（1）①排头与O的距离为S头（m）．等于排头行走的路程+队伍的长300，而排头行进的时间也是t（s），速度是2m/s，可以求出S头与t的函数关系式；②甲赶到排头位置的时间可以根据追及问题的数量关系得出，代入求S即可；在甲从排头返回到排尾过程中，设甲与位置O的距离为S甲（m）是在S的基础上减少甲返回的路程，而甲返回的时间（总时间t减去甲从排尾赶到排头的时间），于是可以求S甲与t的函数关系式；（2）甲这次往返队伍的总时间为T（s），是甲从排尾追到排头用的时间与从排头返回排尾用时的和，可以根据追及问题和相遇问题的数量关系得出结果；在甲这次往返队伍的过程中队伍行进的路程＝队伍速度×返回时间．【解答过程】解：（1）①排尾从位置O开始行进的时间为t（s），则排头也离开原排头t（s），∴S头＝2t+300②甲从排尾赶到排头的时间为300÷（2v﹣v）＝300÷v＝300÷2＝150 s，此时S头＝2t+300＝600m甲返回时间为：（t﹣150）s∴S甲＝S头﹣S甲回＝2×150+300﹣4（t﹣150）＝﹣4t+1200；因此，S头与t的函数关系式为S头＝2t+300，当甲赶到排头位置时，求S的值为600m，在甲从排头返回到排尾过程中，S甲与t的函数关系式为S甲＝﹣4t+1200．（2）T＝t追及+t返回＝+＝，在甲这次往返队伍的过程中队伍行进的路程为：v×（T﹣150）＝v×（﹣﹣150）＝400﹣150v；因此T与v的函数关系式为：T＝，此时队伍在此过程中行进的路程为（400﹣150v）m．【总结归纳】考查行程问题中相遇、追及问题的数量关系的理解和应用，同时函数思想方法的应用，切实理解变量之间的变化关系，由于时间有重合的部分，容易出现错误．25．（10分）如图1和2，▱ABCD中，AB＝3，BC＝15，tan∠DAB＝．点P为AB延长线上一点，过点A作⊙O切CP于点P，设BP＝x．（1）如图1，x为何值时，圆心O落在AP上？若此时⊙O交AD于点E，直接指出PE与BC的位置关系；（2）当x＝4时，如图2，⊙O与AC交于点Q，求∠CAP的度数，并通过计算比较弦AP与劣。

滚动小专题(八) 三角形的外心与内心类型1三角形外心1．已知在△ABC中，AB＝3，BC＝4，AC＝5，则△ABC的外心在(D)A．△ABC内B．△ABC外C．BC边中点D．AC边中点2．(2018·河北模拟)如图，每个小三角形都是正三角形，则△ABC的外心是(B)A．D点B．E点C．F点D．G点3．如图，点O是正八边形ABCDEFGH的中心，则下列说法错误的是(C)A．O是△CEF的外心B．O是△CFG的外心C．O是△OAC的外心D．O是△CDE的外心4．如图是10个相同的正六边形紧密排列在同一平面上的情形．根据图中各点的位置，判断O点是下列哪一个三角形的外心(C)A．△ABD B．△BCD C．△ACD D．△ADE5．某地有四个村庄E，F，G，H(其位置如图所示)，现拟建一个电视信号中转站，信号覆盖的范围是以发射台为圆心的圆形区域．为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小(圆形区域半径越小，所需功率越小)，此中转站应建在(C)A．线段HF的中点处B．△GHE的外心处C．△HEF的外心处D．△GEF的外心处6．在△ABC中，O是它的外心，BC＝24 cm，O到BC的距离是5 cm，则△ABC的外接圆半径为(C) A．11 cm B．12 cm C．13 cm D．14 cm7．如图，在平面直角坐标系xOy中，点A，B，P的坐标分别为(1，0)，(2，5)，(4，2)．若点C在第一象限内，且横坐标、纵坐标均为整数，P是△ABC的外心，则点C的坐标为(7，4)或(6，5)或(1，4)．8．如图，在△ABC 中，∠BAC＝70°，AB ＝AC ，O 为△ABC 的外心，△OCP 为等边三角形，OP 与AC 相交于点D ，连接OA.(1)求∠OAC 的度数； (2)求∠AOP 的度数．解：(1)∵O 为△ABC 的外心， ∴AO 垂直平分BC. ∵AB＝AC ，∴AO 平分∠BAC. ∴∠OAC＝12∠BAC＝35°.(2)∵O 为△ABC 的外心， ∴AO＝CO.∴∠OAC＝∠OCA＝35°.∴∠AOC＝110°. ∵△OCP 为正三角形，∴∠POC＝60°. ∴∠AOP＝50°.类型2 三角形内心9．如图为5×5的网格图，点A ，B ，C ，D ，O 均在格点上，则点O 是(B )A ．△ACD 的外心B ．△ABC 的外心 C ．△ACD 的内心 D ．△ABC 的内心10．如图，△ABC 是等腰直角三角形，点D ，E 在BC 上，△ADE 是等边三角形．若点O 是△ABC 的内心，则下列说法正确的是(C )A ．点O 是△ADE 的内心B ．点O 是△ADE 的外心C ．点O 不是△ABE 的内心D ．点O 是△ABC 的外心提示：易知OA平分∠BAC，由于OA不平分∠BAE，所以点O不是△ABE的内心．11．如图，I点为△ABC的内心，D点在BC上，且ID⊥BC.若∠B＝44°，∠C＝56°，则∠AID的度数为(A) A．174° B．176° C．178° D．180°提示：连接CI，∠AID＝∠AIC＋∠CID＝112°＋62°＝174°.12．如图，△ABC中，AB＝7 cm，AC＝8 cm，BC＝6 cm，点O是△ABC的内心，过点O作EF∥AB，与AC，BC分别交于点E，F，则△CEF的周长为(A)A．14 cm B．15 cm C．13 cm D．10.5 cm提示：连接OA，OB.C△CEF＝CE＋CF＋EF＝CE＋EA＋CF＋FB＝CA＋CB＝14 cm.13．如图，I是△ABC的内心，AI的延长线和△ABC的外接圆相交于点D，连接BI，BD，DC.下列说法中错误的一项是(D)A．线段DB绕点D顺时针旋转一定能与线段DC重合B．线段DB绕点D顺时针旋转一定能与线段DI重合C．∠CAD绕点A顺时针旋转一定能与∠DAB重合D．线段ID绕点I顺时针旋转一定能与线段IB重合提示：根据I是△ABC的内心，得到AI平分∠BAC，BI平分∠ABC，由角平分线的定义得到∠BAD＝∠CAD，∠AB I ＝∠CBI.根据三角形外角的性质得到∠DBI＝∠DIB，根据等腰三角形的性质得到BD＝DI.14．(2018·娄底)如图，P是△ABC的内心，连接PA，PB，PC，△PAB，△PBC，△PAC的面积分别为S1，S2，S3.则S1＜S2＋S3.(填“＜”“＝”或“＞”)15．如图所示，在Rt △ABC 中，∠ACB＝90°，在斜边AB 上分别截取AD ＝AC ，BE ＝BC ，DE ＝6，点O 是△CDE 的外心，则点O 到△ABC 的三边的距离之和是9．提示：由题意知：点O 是EC ，CD 垂直平分线的交点，∵AD＝AC ，BE ＝BC ，∴EC 的垂直平分线经过点B 且平分∠B，CD 的垂直平分线经过点A 且平分∠A.∴点O 是△ABC 的内心．∵∠ACB＝90°，∴r＝12(AC ＋BC －AB)＝12(AD ＋BE －AB)＝12DE ＝3.∴点O 到△ABC 的三边的距离之和是3r ＝9.16．三角形内角平分线的交点为三角形的内心．如图，D 是△ABC 的内心，E 是△ABD 的内心，F 是△BDE 的内心．若∠BFE 的度数为整数，则∠BFE 至少是113°．17．已知I 是△ABC 的内心，AI 的延长线交△ABC 的外接圆于点D ，连接BD.(1)在图1中，求证：DB ＝DI ；(2)如图2，若AB 为直径，且OI⊥AD 于点I ，DE 切圆于点D ，求sin ∠ADE 的值．解：(1)证明：连接BI. ∵I 是△ABC 的内心，∴AD 平分∠CAB，BI 平分∠ABC. ∴∠CAD＝∠BAD，∠ABI＝∠CBI. ∵∠CAD＝∠DBC，∴∠DAB＝∠DBC. ∵∠DBI＝∠DBC＋∠CBI， ∠DIB＝∠DAB＋∠ABI， ∴∠DIB＝∠DBI.∴DB＝DI. (2)连接BD ，DO.∵AB 为直径，∴∠ADB＝90°. ∵OI⊥AD，∴AD＝2DI. ∵BD＝DI ，∴AD＝2BD.∴AB＝AD 2＋BD 2＝5BD.∵DE 切圆于点D ，∴∠ADE＋∠ADO＝90°.又∵∠ADO＋∠ODB＝90°，∠ODB＝∠OBD， ∴∠ABD＝∠ADE.∴sin ∠ADE＝sin ∠ABD＝AD AB ＝2BD 5BD ＝255.。

14．（2020·河北）有一题目:“已知:点O为△ABC的外心，∠BOC=130°，求∠A.”嘉嘉的解答为:画以及它的外接圆O，连接OB，OC，如图8.由∠BOC=2∠A=130°，得∠A=65°.而淇淇说:“嘉嘉考虑的不周全，还应有另一个不同的值.”下列判断正确的是A.淇淇说的对，且∠A的另一个值是115°B.淇淇说的不对，∠A就得65°C.嘉嘉求的结果不对，∠A应得50°D.两人都不对，应有3个不同值图8OBAC答案：A解析：如图1，当∠A是锐角时，△ABC的外心O在其内部，∠A=65°；如图2，当∠A是钝角时，△ABC的外心O在其外部，∵∠1=2∠A，∴∠A=12∠1=12×230°=115°.故∠A=65°或115°，答案为A.10.（2019·河北）根据圆规作图的痕迹，可用直尺成功找到三角形外心的是（）【答案】C23. （2019·河北）如图，△ABC和△ADE中，AB＝AD＝6，BC＝DE，∠B＝∠D＝30°.边AD与边BC交于点P(不与点B，C重合)，点B、E在AD异侧.I为△APC的内心.(1)求证：∠BAD＝∠CAE；(2)设AP＝x，请用含x的式子表示PD，并求PD的最大值；(3)当AB⊥AC时，∠AIC的取值范围为m°＜∠AIC＜n°，分别直接写出m、n的值.第23题图第23题备用图【解题过程】（1）在△ABC和△ADE中，⎪⎩⎪⎨⎧∠DE ＝BC D ＝B ∠AD ＝AB ，∴△ABC ≌△ADE （SAS ），∴∠BAD ＝∠CAE .（2）∵AD ＝6，AP ＝x ，∴PD=AD-AP=6-x.∴当AP 最小时，PD 最大，此时AP ⊥BC.如图所示：第23题答图 1又∵AB ＝6，∠B ＝30°，∴x=AP=21AB=21×6=3， ∴最大PD =6-x=6-3=3.（3）∵AB ⊥AC ，∠B ＝30°，∴∠ACB=60°.∵I 为△APC 的内心，∴∠ACI=21∠ACB=21×60°=30°. ∴∠PAC=2∠IAC=2（180°-30°-∠AIC ）=300°-2∠AIC ，∴∠APC=∠B+∠BAP=30°+90°-∠PAC=120°-（300°-2∠AIC ）=2∠AIC-180°，∵30°＜∠APC ＜120°，∴30°＜2∠AIC-180°＜120°，解得105°＜∠AIC ＜150°，∴m=105，n=150.15．（2018河北省，15，2）如图，点I 为△ABC 的内心，AB ＝4，AC ＝3，BC ＝2，将∠ACB 平移使其顶点与I 重合，则图中阴影部分的周长为（ ）A ．4.5B ．4C ．3D ．2【答案】B【解析】设△ABC 的AB 边上的高为h ，△MNI 的MN 边上的高为r ，周长为a ，则△ABC 的内切圆半径为r ． ∴△第15题图 MN A B CIABC 的面积＝AB·h ＝（AB＋BC＋AC）·r．∴4h＝9r．∴．∵△MNI∽△ABC，∴23．（2018河北省，23，9）如图，∠A＝∠B＝50°，P为AB的中点，点M为射线AC上（不与点A重合）的任意一点，连接MP，并使MP的延长线交射线BD于点N，设∠BPN＝a．（1）求证：△APM≌△BPN；（2）当MN＝2BN时，求α的度数；α的取值范围．【思路分析】（1）根据已知条件可知，△APM与△BPN存在两组对应角及其中一条边对应相等，可证全等；（2）当MN＝2BN时，利用第（1）的结论，可得到△BPN为等腰三角形，从而求出α的度数；（3）根据三角形外心的特点：锐角三角形外心的三角形内部，直角三角形外心在斜边中点，钝角三角形外心在三角形外部可求得α的度数．【解题过程】（1）∵P为AB的中点，∴AP＝BP．1分又∵∠A＝∠B，∠PAM＝∠BPN，∴△APM≌△BPN．2分（2）∵△APM≌△BPN，∴PM＝PN．1分∵MN＝2BN，∴BN＝PN．∴α＝∠B＝50°．2分（3）∵△BPN的外心在该三角形的内部，∴△BPN是锐角三角形．1分∴0°＜α＜90°，0°＜180°－α－50°＜90°．∴40°＜α＜90°．2分23.（2017·河北）如图，16AB=，O为AB中点，点C在线段OB上(不与点O，B重合)，将OC绕点O逆时针旋转270︒后得到扇形COD，AP，BQ分别切优弧CD于点P，Q，且点P，Q在AB异侧，连接OP．(1)求证：AP BQ=；(2)当43BQ=QD的长(结果保留π)；PDBAαC MN第23题图的外心在扇形COD的内部，求OC的取值范围．(3)若APO9.（2016河北，9，3分）图示为4×4的网格图，A，B，C，D，O均在格点上，点O是（）第9题图A．△ACD的外心B．△ABC的外心C．△ACD的内心D．△ABC的内心答案：B6. （2015·河北）如图，AC，BE是⊙O的直径，弦AD与BE交于点F，下列三角形中，外心不是．．点O的是（）A.△ABEB.△ACFC.△AB DD.△ADE【答案】B。

第六单元圆
第21讲圆的基本性质
一、知识清单梳理
最长的弦
弧叫做劣弧、大于半圆的弧叫做优弧
心角：顶点在圆心的角叫做圆心角
还有一个
）经过圆心的直线是该
垂直于弦的直径平分这条弦、并且平分弦所对的两条弧．
的直径垂直于弦、并且平分弦所对的两条弧；
弦的垂直平分线经过圆心、并且平分弦所对的两条弧.
只要满足其中两个、另外三个结论一定成立、即推二知三.
圆心
）定理：一条弧所对的圆周角等于它所对的圆心角的一半
图a 图b 图c 在同圆或等圆中、同弧或等弧所对的圆周角相等的转
径、
点、∠BAC=40°、则∠D的。