和差问题 辅导讲义

第4讲和差问题【学习目标】1、深入了解和差问题；2、提高用数学解决实际问题的能力。

【知识梳理】1、概念：知道两个数的差与这两个数的和，要求两个数各是多少，就是和差问题。

2、公式：（1）大数=（和+差）÷2；（2）小数=（和-差）÷2。

【典例精析】【例1】小张与小王两位同学今年的年龄和是 28 岁，小张比小王大 2 岁，小张今年____岁，小王今年____岁．【趁热打铁-1】华华和英英共有50本漫画书，如果华华给英英5本，则两人的漫画书就一样多，那么原来华华有漫画书____本，英英有漫画书____本．【例2】把一个减法算式的被减数、减数、差加起来和是180，已知减数比差大26，被减数、减数和差各是多少？【趁热打铁-2】丽丽沿着学校长方形操场四周跑了3圈，共跑了1440米．已知这个长方形操场的长宽相差60米，那么操场的面积是____平方米。

【例3】甲乙两所学校共有学生864人。

新学期开学前，由甲校调入乙校32人，这时甲校还比乙校多48人．原来甲校有____个学生．【趁热打铁-3】小苹和小明共有91本故事书，小明给小苹8本以后，小苹比小明多3本，原来小苹有____本故事书．【例4】一些少先队员收集到65千克废金属（包括铜、铁、铝三种），其中铜和铁之和比铝多1千克，而铜比铁多15千克，那么收集到的铜有____千克．【趁热打铁-4】五年级一共有4个班，217人．前两个班的人数总和比后两个班少13，一班比二班多4人，四班比三班少5人，那么一班和四班相差____人．【例5】学校图书馆的书中有420本不是故事书，有400本不是科技书。

已知故事书和科技书一共700本，图书馆里故事书和科技书各有多少本？【趁热打铁-5】老师桌上有一大叠作业本，其中有162本不是一班的，143本不是二班的，一班和二班的共有87本，那么二班的作业本共有____本．【例6】甲筐苹果个数比乙筐苹果多64个，从甲筐中取出____个苹果放入乙筐，可使乙筐苹果比甲筐苹果多12个．【趁热打铁-6】小军有54支铅笔，小红有28支铅笔，小军送给小红____支铅笔后，小军的铅笔数量只比小红多2支．【例7】菜场上有三种蔬菜，其中茄子、辣椒共重50千克，辣椒、黄瓜共重70千克，茄子、黄瓜共重60千克。

和差问题例1小王买了铅笔和圆珠笔共12枝，铅笔比圆珠笔多4枝，问：铅笔与圆珠笔各买了多少枝？随堂练习1小李买苹果、桃子共20个，苹果比桃子多6个，问苹果、桃子各买多少？例2甲、乙两人年龄的和是28岁，甲比乙大6岁，问：甲、乙两人各多少岁？随堂练习2 张丽与王芳年龄的和是26岁，张丽比王芳大4岁，问：张丽、王芳各多少岁？例3甲、乙两人同时写字，8小时两人写了7600个字，甲每小时比乙多写50个字，问：甲、乙两人每小时各写多少字？随堂练习3期末考试，小明语文、数学平均95分，数学比语文多2分，问：小明的语文、数学各得多少分？随堂练习4东、西两个仓库共储棉花6000包，如果将东仓库的棉花600包搬到西仓库，那么两个仓的棉花包数相等，问：原来两个仓库各有多少包棉花？例5 甲、乙两人共收藏图书3200本，乙、丙两人共收藏图书2400本，甲、乙两人共收藏图书2800本，问：甲、乙、丙三人各收藏图书多少本？随堂练习5一个三位数，百位数字与十位数字的和是4，十位数字与个位数字的和是6，百位数字与个位数字的和是10，求这个三位数。

例5小明、小强、小华共栽树100棵，小华比小强多载10棵，小强比小明多栽9棵，问：三人各栽多少棵？随堂练习6A、B、C、D四个数的和是270，A比B多10，比C多25，比D多35，问：这四个数各是多少？综合练习2、小明期中考试，语文和数学的平均分数是97分，语文比数学少6分，语文、数学各得了多少分？3：一部书有上、中、下三册，上册比中册贵1元，中册比下册贵2元，这部书售价32元。

上、中、下三册各是多少元？4：甲、乙两筐香蕉共64千克，从甲筐里取出5千克放到乙筐里去，结果甲筐的香蕉比乙筐的香蕉多2千克。

甲、乙两筐原有香蕉各有多少千克？5：两筐苹果共重90千克,如果从第一筐中取出6千克放入第二筐后,两筐的重量相等,两筐苹果原来各多少千克?6：甲乙两船共载客623人,若甲船增加34人,乙船减少57人,这时两船乘客同样多,甲船原有乘客多少人？7：师徒两人合做3小时，共生产零件165个，师傅每小时比徒弟多生产5个，师徒两人每小时各生产零件多少个？8：甲的年龄数字颠倒过来恰好是乙的年龄，二人年龄之和为99岁，甲比乙大9岁，求甲的年龄？9：在减法算式中，被减数、减数、差三数之和是2002，减数比差大123，减数是多少？10：甲、乙、丙三个数，和为300，已知甲比乙大50，乙比丙大20，甲数是多少？11：甲、乙、丙三个人同时参加储蓄。

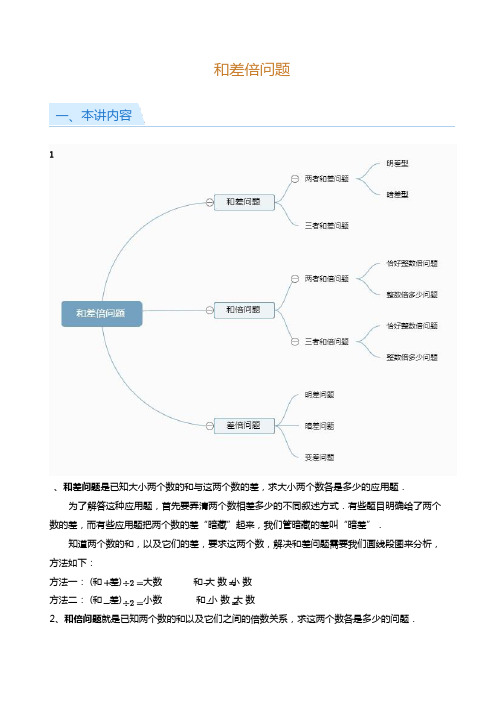
和差倍问题一、本讲内容、和差问题是已知大小两个数的和与这两个数的差，求大小两个数各是多少的应用题．为了解答这种应用题，首先要弄清两个数相差多少的不同叙述方式．有些题目明确给了两个数的差，而有些应用题把两个数的差“暗藏”起来，我们管暗藏的差叫“暗差”．知道两个数的和，以及它们的差，要求这两个数，解决和差问题需要我们画线段图来分析，方法如下：方法一： (和差) 大数和大数小数方法二： (和差) 小数和小数大数2、和倍问题就是已知两个数的和以及它们之间的倍数关系，求这两个数各是多少的问题．解答此类应用题时要根据题目中所给的条件和问题，画出线段图，使数量关系一目了然，从而找出解题规律，正确迅速地列式解答．和倍问题的特点是已知两个数的和与大数是小数的几倍，要求两个数，一般是把较小数看作倍数，大数就是几倍数，这样就可知总和相当于小数的几倍了，可求出小数，再求大数．和倍问题的数量关系式是：和( 倍数) 小数小数倍数大数或和小数大数如果要求两个数的差，要先求份数：份数(倍数) 两数差．解决和倍问题，关键是学会画线段图，这样可以帮助我们更好的弄清各数量之间的关系．、差倍问题就是已知大小两数的差，以及大小两数的倍数关系，求大小两数的问题．差倍问题的特点与和倍问题类似．解答差倍问题的关键是要确定两个数量的差及相对应的倍数差，一般情况下，在题目中不直接给出，需要经过调整和计算才能得到．解题思路：首先要在题目中找到倍量，然后画图确定解题方法．被除数的数量和除数的倍数关系要相对应，相除后得到的结果是一倍量．差倍问题的基本关系式：差( 倍数) 倍数(较小数)倍数几倍几倍数(较大数) 或较小数差较大数解决差倍问题，关键是学会画线段图，这样可以帮助我们更好的弄清各数量之间的关系．二、例题精讲1. 例题暑期课结束时，小俊与小强的电子积分总共有分，小俊的积分比小强多分，小强的积分为分．哥哥和妹妹二人共有图书本，哥哥的图书数量比妹妹多本，妹妹有图书本．小灰灰和懒羊羊共有块糖，小灰灰给懒羊羊块后，两人就一样多了，问原来两人各有多少块糖？2. 巩固甲、乙两人共有存款元, 甲取出元, 乙存入元后, 两人的存款一样了求原来甲有存款元．小兰期来考试时语文和数学平均分是分，数学比语文多分，问小兰语文和数学分别多少分？3. 和倍问题两者和倍问题4. 例题艾迪和薇儿一共有块糖，艾迪糖的数量是薇儿的倍，那么艾迪有块.艾迪和薇儿有贺卡张，薇儿的卡片张数是艾迪的倍，薇儿艾迪各有多少张？5. 巩固图书馆购进《水浒传》和《三国演义》两种图书共本，已知《水浒传》比《三国演义》的倍还要少本，那么购进《三国演义》本，《水浒传》本．两只狗熊掰玉米，两只狗熊一共掰了个玉米，大狗熊掰的玉米数量是小狗熊的倍还多个，那么大狗熊一共掰了个玉米．三者的和倍问题6. 例题甲乙丙三数的和是，已知甲数是乙数倍，丙数是乙数的倍，乙数为．刘老师、连老师和杨老师一共张积分卡，其中刘老师的积分卡是杨老师的倍，连老师的积分卡是杨老师的倍，那么三位老师分别有多少张积分卡？7. 巩固果园里有桃树、梨树、苹果树共棵．桃树比梨树的倍多棵，苹果树比梨树少棵，求桃树、梨树和苹果树各有多少棵？甲、乙、丙三人共有张积分卡，甲比乙多张，丙是乙的两倍少张，则乙有张积分卡．8. 差倍问题明差问题9. 例题加加和减减比赛折千纸鹤，比赛结束后发现加加折的千纸鹤比减减多只，而且加加折的是减减折的千纸鹤的倍，请问减减的千纸鹤有只，加加有只．加加和减减比赛投篮，比赛结束后发现加加投中的比减减多个，而且加加投中的是减减的倍，请问减减投中个，加加投中个．10. 巩固学校买来一些白板笔，其中蓝笔比红笔少箱，红笔比蓝笔的倍还多箱，学校买来蓝笔箱．薇儿和妈妈一起包饺子．妈妈包的饺子比薇儿的倍多个，并且妈妈比薇儿多包了个，那么薇儿包了个饺子，妈妈包了个饺子．暗差问题11. 例题甲桶有油千克，乙桶有油千克，两桶油卖出同样多之后，甲桶油成为了乙桶油的倍，那么每桶油卖出了千克．12. 巩固甲桶的纯净水比乙桶多升，两桶中的水都被喝掉升后，甲桶的水量是乙桶的倍，原来乙桶中的纯净水有升．变差问题13. 例题两个仓库所存的粮食重量相等，如果从第一个仓库取出千克粮食放入第二仓库，那么第二仓库重量就是第一仓库的倍．问这两个仓库各有存量多少千克？纺织厂男女职工人数一样多，如果调走名男职工，又转入名女职工，此时女职工人数是男职工人数的倍，那么纺织厂原有男职工多少人？14. 巩固新家有大小两个书架，大书架上书的本数是小书架的倍，如果从大书架上取走本放到小书架上，那么两个书架上的书一样多，小书架上原来有本书，大书架上原来有本书．甲、乙俩人存款若干元，甲存款是乙存款的倍．如果甲取出元，乙存入元，甲、乙的存款正好相等．问甲、乙俩人原来各存款多少元？。

和差问题教学目标: 1,了解和差问题 ,掌握解决问题的方法,初步形成解决此类问题的一般性策略. 2,通过本节课的学习启迪学生思维,,培养学生思维能力,改善学生的思维品质.教学重点;和差问题的解题方法及思路。

教学难点;,形成策略思想，形成思维策略，进行策略化解题。

知识点，公式（和+差）÷2=较大数（和-差）÷2=较小数和-较大数=较小数和-较小数=较大数较大数-差=较小数较小数+差=较大数教学过程例一,参加体验夏令营的学生共有96人,男生比女生多8人,男生女生各有多少人?习1，甲乙两桶油共重100千克，已知甲桶比乙桶少油20千克，甲乙两桶油原来各有油多少千克？习2，数学兴趣小组有学生35人，男生比女生多3人，这个兴趣小组男生和女生各有多少人?暗差，有些题把两个数的差“暗藏”起来，我们管暗藏的差叫“暗差”例二，今年小强7岁，爸爸35岁，当两人年龄和是58岁时，两人年龄各是多少岁？习1，今年小刚和小强两人年龄和为22岁，一年前，小刚比小强大4岁，今年小刚和小强各是多少岁？习2、粮仓运来面粉和大米共4820千克，面粉比大米多20袋，每袋重50千克。

粮仓运来面粉、大米各多少千克？例三，甲乙两书架共有书480本，如果从甲书架中取出40本放入乙书架中，这时两个书架的本数正好相等，甲乙两个书架原来各有多少本书？习1,两筐苹果共有180个，从乙筐中拿出15个放入甲筐，这时两筐苹果的个数相等。

甲乙两筐原来各有苹果多少个？习2,.甲、乙两筐苹果共76千克,从甲筐取出5千克苹果放入乙筐里,甲乙两筐苹果就一样多,.甲、乙两筐原各有苹果多少千克?例四,甲乙两桶油共重196千克，从甲桶往乙桶倒10千克后，还比乙桶多2千克。

甲桶和乙桶原来各有油多少千克？习1,甲乙两个修路队共有1980人参加修路,从甲队调出285人到乙队, 这时乙队比甲队还少24人,求甲乙两队各有多少人?习2,、甲、乙两个学校共有1245人，如果从甲校调20人去乙校后，甲校比乙校还多5人，两校原有学生各有多少人？例五甲乙两人共有150元钱,如果甲增加13元,而乙减少27元,那么两人的钱数就相等,求甲乙两人各有多少元?习1,甲乙两船共有乘客623人,如果甲船增加34人,乙船减少57人,那么两船的乘客同样多,求甲乙船各有多少乘客?习2, 纺织厂第一车间和第二车间共有工人48人，如果从第一车间调出8人，第二车间增加4人,第一车间的人数比第二车间还多2人。

第9讲和倍、差倍、和差问题（讲义）小学数学，第9讲和倍、差倍、和差问题（讲义）教案一、教学目标1.理解和运用和倍、差倍、和差问题的概念和方法，能够准确解决这类问题；2.讲师能在教学中引导学生从整体上掌握递增、递减、加减的基本方法，从而提高学习效率；3.通过本课程教学，增强学生数学思维意识，提高数学运算技能和思维能力。

二、教学内容1.和倍问题2.差倍问题3.和差问题三、教学重点和难点1.重点：掌握理论并能综合运用2.难点：将理论知识应用到实际问题中四、教学方法1.讲解法：通过清晰、简单的语言，讲解概念、规律和方法；2.演示法：通过实例进行演示，让学生更好地理解概念和方法；3.互动法：通过提问、解决问题等互动方式，促进学生思考和交流。

五、教学过程设计Step1. 引入（1）引导学习者回忆前几讲中学到的知识点：比较大小，加减法、三位数的读法等。

（2）通过实例介绍“和倍、差倍、和差”这三种问题，并引导学生初步掌握这些概念。

（3）引导学生了解“等差数列”的简单概念，并列举一些有关数字的整数和小数。

Step2. 正文（1）和倍问题1）完整问题：已知某个数，在这个数上加另外一个数，两者之和再乘以一固定倍数，可得另一个数。

如果已知此数和乘数，求另外一个数。

2）解题步骤：假设这个数为X，另外的数为Y，倍数为N，可以列出下面的等式：X+Y=Z；(Z×N)/2=Y（2）差倍问题1）完整问题：已知某个数，将另外一个数从其上减去，然后将差乘以一固定倍数，可得另外一个数。

如果已知此数和乘数，求另外一个数。

2）解题步骤：假设这个数为X，另外的数为Y，倍数为N，可以列出下面的等式：X-Y=Z;(Z×N)/2=Y（3）和差问题1）完整问题：已知某个数，在这个数的基础上，加上一定的值后，再减去一定的值，可求出一个差，将这个差乘以一固定倍数，可得另外一个数。

如果已知这个数、值和乘数，求另外一个数。

2）解题步骤：假设这个数为X，增量为A，减量为B，倍数为N，可以列出下面的等式：(X+A)-B=Z;(Z×N)/2=Y;Step3.练习与拓展（1）练习题 1：已知4，含量比9高1%的另外一种物品，质量是该物品的4/3，求该物品的质量。

和差问题第一讲一、兴趣导入 (Topic-in):趣味分享麒麟飞到北极变什么啊？答案：冰激凌世界上什么鸡跑的快？答案：肯德鸡块一片大草地（植物）答案：梅花（没花）又一片大草地（植物）答案：野梅花来了一群羊（水果）答案：草莓来了一群狼（水果）答案：杨梅来了一群狮子（体坛名将）答案：郎平什么动物最没有方向感？答案：麋鹿（迷路）二、学前测试 (Testing):问答题（口答）1、鸡兔同笼问题的公式？三、知识讲解 (Teaching) ：基础知识说到“和差问题”，小学高年级的同学，人人都会说：“我会！”和差问题的计算太简单了.是的，知道两个数的和与差，求两数，有计算公式：大数 =（和 +差）÷ 2小数 =（和 - 差）÷ 2会算，还要会灵活运用，要把某些应用题转化成和差问题来算.先看几个简单的例子 .例 1 张明在期末考试时，语文、数学两门功课的平均得分是 95 分，数学比语文多得 8 分，张明这两门功课的成绩各是多少分？解： 95 乘以 2，就是数学与语文两门得分之和，又知道数学与语文得分之差是8.因此数学得分 =（95×2＋8）÷ 2＝99.语文得分 =(95 × 2-8 ）÷ 2＝ 91.答：张明数学得99 分，语文得 91 分.注：也可以从 95 ×2-99 ＝91 求出语文得分 .例 3、两筐水果共重 150 千克，第一筐比第二筐少10 千克，两筐水果各多少千克？例 2 有 A，B，C 三个数， A加 B 等于 252 ，B加 C 等于 197 ， C 加 A 等于 149 ，求这三个数.解：从 B+C＝197 与 A+C＝149，就知道 B与 A 的差是 197-149 ，题目又告诉我们，B 与 A 之和是 252. 因此B=（ 252＋ 197-149 ）÷ 2 ＝ 150 ，A＝252-150 ＝102，C＝149-102 ＝47.答： A， B， C 三数分别是 102，150，47.注：还有一种更简单的方法（A+B）＋（ B＋ C）＋（ C＋A）＝ 2×（ A＋B＋C）.上面式子说明，三数相加再除以2，就是三数之和 .A＋B＋C＝（ 252＋ 197＋149）÷ 2＝ 299. 因此C＝299-252 ＝47，B＝299-149 ＝150，A＝299-197 ＝102.例 3 甲、乙两筐共装苹果 75 千克，从甲筐取出 5 千克苹果放入乙筐里，甲筐苹果还比乙筐多 7 千克 . 甲、乙两筐原各有苹果多少千克？解：画一张简单的示意图，就可以看出，原来甲筐苹果比乙筐多5＋7＋ 5 ＝ 17 （千克）因此，甲、乙两数之和是75 ，差为 17.甲筐苹果数 =（ 75＋17）÷ 2＝ 46 （千克） .乙筐苹果数 =75-46 ＝29（千克） .答：原来甲筐有苹果46 千克，乙筐有苹果29 千克 .例 3、长方形操场的长与宽相差 80 米，沿操场跑一周是 400 米，求这个操场的长与宽是多少米？【解析】长方形一周的长是指两条长和两条宽的和，由条件可知一条长与一条宽的和为400 2 200 (米)，由此我们就知道了长和宽之和是200 米，又知道长和宽之差是80 米，根据和差问题来解答：方法一：长：（20080） 2140 (米)宽： 1408060（米）方法二：宽：（20080） 260(米)长： 6080140（米）例 4 张强用 270 元买了一件外衣，一顶帽子和一双鞋子 . 外衣比鞋贵 140 元，买外衣和鞋比帽子多花 210 元，张强买这双鞋花多少钱？解：我们先把外衣和鞋看成一件东西，它与帽子的价格和是270 元，差是 210 元 .外衣和鞋价之和 =（270＋ 210 ）÷ 2＝ 240 （元） .外衣价与鞋价之差是140，因此鞋价 =（ 240-140 ）÷ 2＝50（元） .答：买这双鞋花50 元 .四、强化练习 (Training)：1、甲、乙两人同时以相同的速度打字，2分钟共打了240个字，已知甲每分钟比乙多打 10 个字．问甲、乙两人每分钟各打多少个？2、甲乙两筐水果共 40 千克，如果从甲筐那 6 千克放入乙筐，甲的就比乙的多 2 千克。

第3讲和差问题【学习目标】1、学习了解和、差的变化规律；2、利用这些规律来解决一些较简单的问题。

【知识梳理】1、和差问题：已知两个数的和与差，求出这两个数各是多少的应用题，叫和差应用题。

2、解答和差应用题的基本数量关系是：（和－差）÷2=小数（和＋差）÷2=大数【典例精析】【例1】期中考试薇薇和龙龙数学成绩的总和是178分，龙龙比薇薇少2分。

两人各考了多少分？【趁热打铁-1】两筐苹果共重85千克，第一筐比第二筐多3千克。

两筐苹果各重多少千克？【例2】把长88厘米的铁丝围成一个长方形，使宽比长少2厘米。

长和宽各是多少厘米？【趁热打铁-2】果果沿着学校长方形操场四周跑了3圈，共跑了1800米．已知这个长方形操场的长宽相差100米，那么操场的长是____米，宽是米。

【例3】把一个减法算式的被减数、减数、差加起来和是180，已知减数比差大10，被减数、减数和差各是多少？【趁热打铁-3】在一个减法算式里，被减数、减数与差这三个数之和是2200，减数比差大100，减数是________．【例4】凯凯和新新买了66个面包，新新比凯凯每周少吃3个，二人恰好用了6周吃完了所有的面包．求凯凯每周吃多少个面包？【趁热打铁-4】一列客车和7辆同样的小汽车共载客77人，客车比小汽车多承载了7人，则客车载了____人，每辆小汽车载了____人．【例5】笑笑与达达两位同学2年前的年龄和是24岁，且笑笑比达达大 2 岁，笑笑今年____岁，达达今年____岁．【趁热打铁-5】今年爸爸比妈妈大4岁，再过5年，爸爸和妈妈年龄和是80岁，今年爸爸______岁，妈妈______岁．【例6】甲乙两船共载客730人，若甲船增加34人，乙船减少56人，这时两船乘客同样多，甲船原有乘客_______人．【趁热打铁-6】培培某次考试的语文和数学成绩一共185分，若语文多考3分，数学少考2分，语文和数学就一样，那么语文分，数学分。

和差问题讲义给出两个数可以求出它们的和与差。

如：15；12.15+12=27； 15－12=3 两个数的和与差同奇偶给出两个数的和与差可以求出这两个数。

两个数的和和是27，两个数的差3，求,这两个数。

大--------------- 小------------b 能整除a ：计作b │a a 倍数 b 约数。

1. 0是任何自然数的倍数；2. 1是任何自然数的约数；3. 一个整数的个位上是0、2、4、6、8中的某一个。

这个数能被2整除。

4. 一个整数的个位上是0或5。

这个数能被5整除。

5. 一个整数的各数位上数字的和能被3（或9）整除。

这个整数也能被3（或9） 整除。

6. 一个整数的末两位数能被4（或25）整除。

这个整数也能被4（或25）整除。

7. 一个整数的末三位数能被8（或125）整除。

这个整数也8. 一个整数即能被2整除，又能被3整除。

这个整数能被6整除。

9. 一个整数奇数位上的数字之和与偶数位的数字之和的差能被11整除。

这个整数能被6整除。

10. 一个整数的末三位数与末三位以前数字所组成的书之差能被7（11或13）整除。

这个整数也能被7（11或13）整除。

数的整除性质：１．如果数c │a 、c │b ，则c │（a+b ）、c │（a-b ）。

２．如果数b │a 、c 是整数，则b │ac 。

３．如果数b │a 、c │b ，则c │a 。

和补一个差=大数的两倍， （和+差）=大数×2（和+差）÷2=大数 和去掉一个差=小数的两倍，（和差）=小数×2 （和－差）÷2=小数４．如果数b│a 、c│a。

则bc│a。

数图形A B C D【思路导航】我们可以采用以线段左端点分类数的方法。

以A点为左端点的线段有：AB、AC、AD 3条；以B点为左端点的线段有：BC、BD2条；以C点为左端点的线段有：CD l条。

所以，图中共有线段3+2+1=6(条)。

我们还可以这样想：把图中线段AB、BC、CD看做基本线段来数，那么，由l条基本线段构成的线段有：AB、BC、CD 3条；由2条基本线段构成的线段有：AC、BD 2条；由3条基本线段构成的线段有：AD l 条。